Random Positions of Dendritic Spines in Human Cerebral Cortex

Abstract

Dendritic spines establish most excitatory synapses in the brain and are located in Purkinje cell's dendrites along helical paths, perhaps maximizing the probability to contact different axons. To test whether spine helixes also occur in neocortex, we reconstructed >500 dendritic segments from adult human cortex obtained from autopsies. With Fourier analysis and spatial statistics, we analyzed spine position along apical and basal dendrites of layer 3 pyramidal neurons from frontal, temporal, and cingulate cortex. Although we occasionally detected helical positioning, for the great majority of dendrites we could not reject the null hypothesis of spatial randomness in spine locations, either in apical or basal dendrites, in neurons of different cortical areas or among spines of different volumes and lengths. We conclude that in adult human neocortex spine positions are mostly random. We discuss the relevance of these results for spine formation and plasticity and their functional impact for cortical circuits.

Introduction

Dendritic spines (i.e., spines) are sites of most excitatory synapses in the cortex and are considered key for learning, memory, and cognition since the times of Cajal (Ramón y Cajal, 1899). Indeed, spine densities and the absolute number of spines in basal dendritic arbors of pyramidal cells in different cortical areas increase in the primate lineage (Benavides-Piccione et al., 2002; Elston and DeFelipe, 2002), although the distribution of spines as a function of distance from the soma is remarkably constant across species, indicating a similarity in their function in pyramidal neurons (Elston and DeFelipe, 2002).

In cerebellar Purkinje cells from fish and mice, spines form regular linear arrays tracing short-pitch helical paths (O'Brien and Unwin, 2006). These intriguing results suggest a spatial maximization for spines to interact with different axons, enhancing the potential connectivity of spines (Chklovskii et al., 2002). To examine the generality of these findings, we studied 3D reconstructed pyramidal neurons from adult human cortex and tested whether their spines were also arranged in helixes. We used autopsy material from two normal male subjects of different ages and performed Lucifer yellow (LY) injections into layer 3 pyramidal neurons of lightly fixed samples from three different cortical areas. After immunocytochemical enhancement of the fluorescence, we performed volumetric imaging of 510 dendritic segments from these neurons and performed Fourier and spatial statistical analysis of the insertion point of spines, testing whether or not they were spatially structured. The majority of samples did not reveal spine helixes, and the positioning of spines along dendrites could not be distinguished from the null hypothesis of random location.

Materials and Methods

Tissue preparation.

Human tissue from two male subjects (40 and 85 years) was obtained at autopsy (2–3 h postmortem). The cause of death was traffic accident (Case C40) and pneumonia (plus interstitial pneumonitis; Case C85). Brains were immediately immersed in cold 4% PFA (in phosphate buffer [PB], pH 7.4) and sectioned into 1.5-cm-thick coronal slices. Small blocks of cortex (∼15 × 10 × 10 mm) were then transferred to 4% PFA in PB for 24 h at 4°C. Tissue from cytoarchitectonically identified frontal, temporal, and cingular cortex (Brodmann's areas 10, 20, and 24, respectively) was used.

Staining.

Coronal sections (250 μm) were obtained with a vibratome and labeled with DAPI (Sigma) to identify cell bodies. Pyramidal cells in layer 3 were then individually injected with LY (8% in 0.1 m Tris buffer, pH 7.4) by continuous current until the distal tips of each cell fluoresced brightly, indicating that the dendrites were completely filled, ensuring that the fluorescence did not diminish at a distance from the soma (Elston and Rosa, 1997; Elston et al., 2001; Benavides-Piccione et al., 2013). Sections were then stained with rabbit antisera against LY (1:400,000; Cajal Institute) diluted in stock solution (2% BSA, 1% Triton X-100, 5% sucrose in PB). Sections were then incubated in biotinylated donkey anti-rabbit IgG (1:100; GE Healthcare) and AlexaFluor-488 streptavidin-conjugated (1:1000; Invitrogen). Finally, sections were mounted in 50% glycerol in PB.

Imaging.

Sections were imaged with a Leica TCS 4D confocal scanning laser and a Leitz DMIRB fluorescence microscope (491 nm excitation). Horizontally projecting dendrites were randomly selected, each from a different pyramidal neuron. Images stacks (∼100 μm dendritic length; n = 510 stacks; z-step of 0.28 μm; see Fig. 1) were acquired at high magnification (63× glycerol; 3.2 zoom) (Benavides-Piccione et al., 2013). A total of 510 dendritic segments (176 frontal, 135 temporal, and 199 cingular), 77 from apical (23 frontal, 27 temporal, and 27 cingular), and 433 from basal (153 frontal, 108 temporal, and 172 cingular) regions were acquired. The 433 basal segments included 144 dendrites (51 frontal, 36 temporal, and 57 cingular), complete from the soma to the distal tips. Apical dendrites were scanned at 100 μm distance from soma (because dendrites were virtually devoid of spines for the first 80–90 μm). Confocal parameters were set so that fluorescence signal was as brightest as possible but assuring that there were no pixels saturation within the spines.

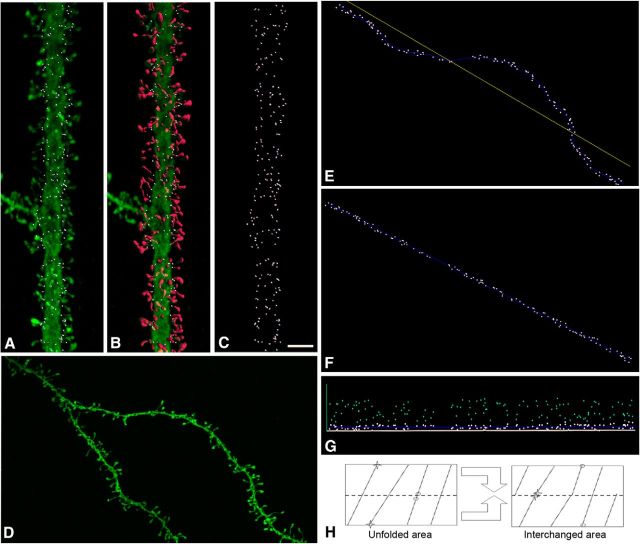
Figure 1.

Spine insertion point analysis in human pyramidal cell dendrites. A, Confocal microscope image showing an example of a labeled apical dendrite. For each individual dendritic spine, its point of insertion (white dots) in the dendritic shaft was manually determined. B, 3D reconstruction of each individual dendritic spine is shown in red. C, Projection image showing points of insertion in the same dendritic segment. Scale bar: (in C) A–D, 4 μm. D, Another example of a dendritic segment. E, Insertion point of spines (white dots) in the upper part of the dendritic segment shown in D. F, G, Straightening (F) and unrolling (G) tranformations to locate the 3D position of points in an unfolded arrangement (light blue dots). H, Area transformation to obtain an estimator of G(r). The unrolled distribution is “cut” by half (dotted line), and the pieces are “glued” to correct for edge effect bias. Note the new positions of neighbor points (circles and stars) after the new arrangement.

Fourier analysis.

Projection images of dendrites were used for this analysis. Fourier transforms were generated with the Medical Research Council image-processing software (Crowther et al., 1996) as in O'Brien and Unwin (2006). Curvature was corrected by a spline-fitting procedure, and filtered images were “boxed-off,” equalized to yield an average density equal to the average value around the box perimeter (see Fig. 2). Fourier transforms were then calculated and displayed as diffraction patterns. Filtered images were obtained by inversed Fourier of terms included in masked-out regions in the transform.

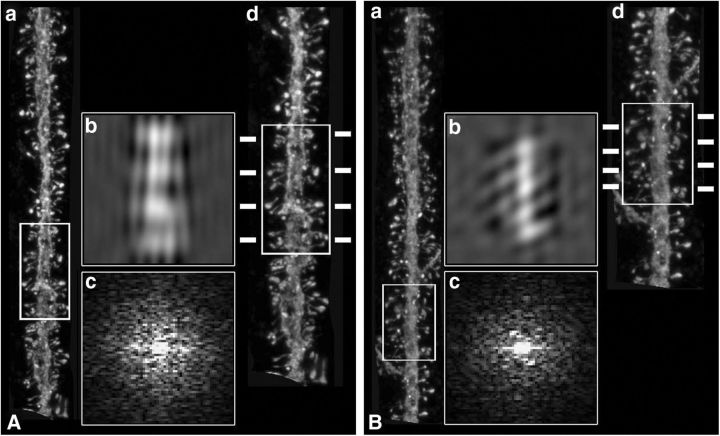
Figure 2.

Fourier analysis. A, B, Two examples of dendritic segments from apical dendrites (a), showing regions in which helical distributions were apparent (white boxed areas), after the corresponding Fourier and inverse Fourier transforms (b, c). (d) Higher-magnification images of the same dendritic segments indicating possible frequency of regular spacing along the lateral insertion of dendritic spines (dashes).

Spatial statistical analysis.

For each spine, its point of insertion (see Fig. 1A–C) in the dendritic shaft was manually determined, while rotating the image in 3D, using Imaris 6.4.0 (Bitplane). Spine length was manually marked from point of insertion in dendritic shaft to distal spine tip. Spines from some dendritic segments were completely reconstructed in 3D using thresholds selected to constitute a solid surface (Benavides-Piccione et al., 2013). All spines were included in the analysis, regardless of their morphology. We then used a software tool based on the implementation of straightening and unrolling transformations, to analyze 3D points of insertion in a planar, unfolded arrangement (Fig 1D–G) (Morales et al., 2012). We used these unfolded arrangement of insertions of spines as a spatial point pattern to test whether they are equally likely to occur at any location within the study area, regardless of the location of other insertion points. This statistical independent distribution is known as the complete spatial randomness (CSR), whose underlying mathematical model is a homogeneous spatial Poisson point process.

We tested for CSR by computing the G(r) summary function for each distance r (nearest neighbor distance distribution function). G(r) was estimated from Ĝ(r), the cumulative frequency distribution of the observed nearest-neighbor distances between insertion points. Under the null hypothesis of CSR, this function is G_CSR(r) = 1 − exp(−λπr²), where λ denotes the intensity of the homogeneous spatial Poissson process, that is, the number of insertion points per unit area. Deviations of the estimator Ĝ(r) from G_CSR(r) indicate deviations from CSR. We measured this deviation via “envelopes” (confidence bands) around G_CSR(r) obtained through Monte Carlo simulations. If Ĝ(r) was outside the envelope region for some r, the null hypothesis was rejected. We built R implementations for G(r) and Monte Carlo envelopes with spatstat functions Gest and envelope. We also introduced a correction in the usual estimation of G(r) for the edge effect bias. This correction was needed to avoid the influence of the observation window and correct problems arising from the unfolding transformation of the original insertion 3D points because points close in the original 3D space could end up farther from each other because of the unfolding operation (see Fig. 1H; left, stars). Our edge correction exchanged the two halves obtained by cutting the unfolded area horizontally (see Fig. 1H, right) so those points were then close. Because other points suffered the opposite effect (see Fig. 1H, circles), the nearest neighbor distance used in Ĝ(r) was defined as the minimum between the distances in the unfolded area (left) and in the area after the exchange (right).

Results

Fourier analysis selection of helical patterns

To search for spine helixes in pyramidal neurons, we three-dimensionally reconstructed pyramidal neurons from adult human cortex from autopsy material from two patients of different ages by performing LY injections into layer 3 pyramidal neurons, performing immunocytochemical enhancement of the fluorescence, and carrying out volumetric imaging of a total of 510 dendritic segments (see Materials and Methods). These included apical and basal dendritic segments from 3 cortical areas.

To uncover possible helical distribution patterns, spatial Fourier transforms were applied for each dendritic segment (7- to 15-μm-long; see Fig. 2). Helixes were defined by the symmetric periodicities in the Fourier transforms (see Fig. 2Ac,Bc), as well as periodic repeats in the spine insertions, as visualized in the inverted images generated from the Fourier terms boxed symmetrically (see Fig. 2Ab,Bb). After visual inspection of these Fourier transforms, we selected some examples where potential helixes were suspected (60 of 510). For these cases, we calculated an interspine spacing, based on the symmetrical helical terms inverted Fourier images, and superimposed it on the original image to match the lateral insertion points of spines (see Fig. 2Ad,Bd). These results were consistent with the original description of spine helixes in the cerebellum, although at the same time, the clarity of the helical side components in the Fourier transforms in our samples did not match those of O'Brien and Unwin (2006) (compare Fig. 2Ac,Bc with O'Brien and Unwin, 2006, their Figs. 2C and 3B). Thus, although we encountered some evidence for helical patterns, these were present in a minority of samples and their Fourier signatures were not strong.

Figure 3.

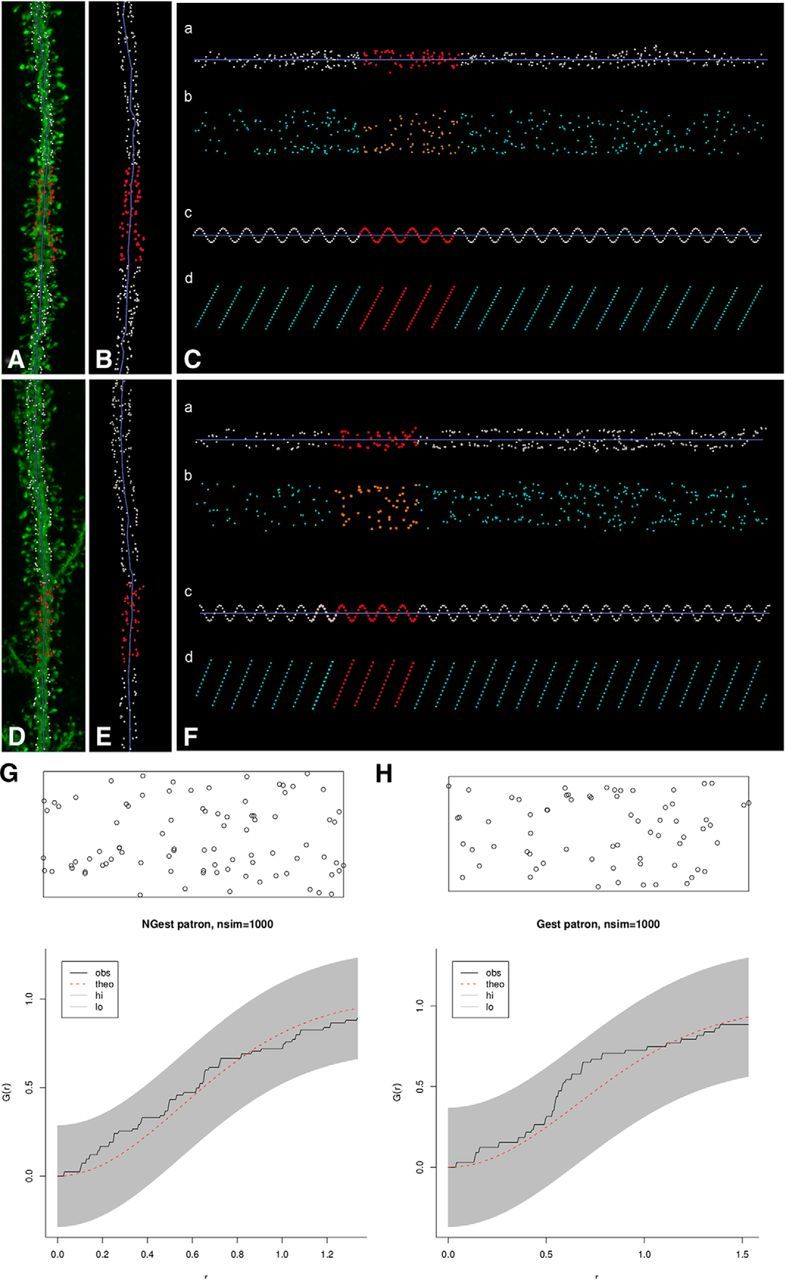
Unstructured positioning of insertion points. A, D, Same dendritic segments as in Figure 2, along with points of insertion of spines (white dots). Red dots represent the white boxed areas from Figure 2, with potential spine helixes. B, E, Insertion points of dendritic spines of dendritic segments from A and D. C, F, Unfolded arrangement of the insertion points in B, E, after straightening (a) and unrolling (b). Artificial helical patterns, containing the same number of points as in the real dendrite, were created for comparison in each example (c). d, The corresponding unrolling process for the helical samples. G, H, Monte Carlo envelope tests of these examples. Graphs represent allowed random band (shaded), the theoretic distribution function G_CSR(r) (red dotted line), and the estimated Ĝ(r) obtained from the patterns analyzed (black line) using the proposed edge correction. Because examples did not surpass the shaded envelope, the null hypothesis of complete spatial randomness (CSR) was not rejected.

Visual analysis of spine insertion points with straightening and unrolling transforms

Of the 60 Fourier transforms showing potential helical distributions, the most promising 11 dendritic segments (5 apical and 6 basal; typically ∼100 μm long) from the cingulate cortex were analyzed using straightening and unrolling methods. The point of insertion of each spine was manually determined in 3D (Fig. 1). Then, we visualized spine distributions based on straightening and unrolling the insertion points (see Materials and Methods). Visual distribution of points in an unfolded arrangement showed no clear distributions (Fig. 3A–F). To help with this analysis, artificial helical patterns of different frequencies were created displaying the expected regular arrangement of helical spines in the unrolled transforms (Fig. 3Cc,Cd,Fc,Fd). To further analyze spine positions, the point of insertion was identified in 7600 individual spines from 64 additional randomly selected dendritic segments (n = 10 apical; n = 54 basal) and examined using the same straightening and unrolling methodology. In none of the cases did we visually distinguish helical patterns. Similar analyses were performed using terminal points at spine tips, instead of the insertion points, to test whether the position of the putative synaptic contacts could follow a possible recognizable pattern. Again, no helical patterns were visually distinguished.

Spatial statistical analysis of spine distributions

To quantitatively examine the spatial distribution of spine insertion points, we used the same 75 dendritic segments analyzed in the unfolded arrangement (including the 11 showing potential helical distributions by Fourier analysis), and tested whether CSR functions could account for their spine distribution, by creating libraries for Monte Carlo simulations. For each dendritic segment, we generated 1000 CSR simulations for constructing the statistical envelopes (α = 0.001). The null hypothesis of CSR was only rejected in 2 of the 75 segments. For the nonrejected 73 cases, λ intensities ranged from 0.1014 to 0.5638 spines per μm² (Fig. 3G,H). The same tests were performed over the terminal points at the distal tip of the spine, obtaining also nonrejected null hypotheses (data not shown).

To test whether CSR tests were capable of discriminating the possible presence of complex helical patterns, 200 double helical patterns were generated artificially from a simple set of 120 helices with constant helix lengths, amplitudes and number of samples, and changing helix frequency and phase. In the frequency modulation dataset, 20 cases were built changing the number of spirals per unit length. For phase modulation, we constructed six variants equally spaced in the interval (0, 360). To assemble the 200 double helical patterns, we chose random pairs among the 120 helices available. For all these control datasets, the null hypothesis of CSR was rejected.

Analysis of spine distributions according to spine volumes and lengths

Because the size and length of spines are variable (Arellano et al., 2007), we also analyzed possible spatial distribution based on a particular spine morphology by using different spine length and volume filters (Fig. 4A–H). Spines from 75 dendritic segments from apical and basal dendrites of both individuals were fully reconstructed in 3D to estimate spine volumes and lengths. Such information enabled us to selectively visualize, in the unfolded arrangement, the longer/shorter and/or the larger/smaller spines. Spine distributions were analyzed according to six filters: small (<0.3 μm³), medium (0.3–0.5 μm³), and large spines (>0.5 μm³); short (<1 μm), medium (1–2 μm), and long (>2 μm) spines. Combinations of both filters were also tested (e.g., small and short, small and medium length) in basal and apical dendrites from both individuals. For all samples, we were not able to visually detect helical patterns. To statistically analyze the spatial distribution of these subpopulations of spines, we again used the CSR distribution as null hypothesis to test for nonrandomness in distributions of longer/shorter and/or the larger/smaller spines using the same combinations and filters described. The dataset consisted of 675 subsets of spines, obtained from the 9 combinations of filters over the same 75 dendritic segments. The null CSR hypothesis was used for 253 subsets because the remaining combinations contained <3 spines. The null hypothesis CSR was not rejected for any of the cases.

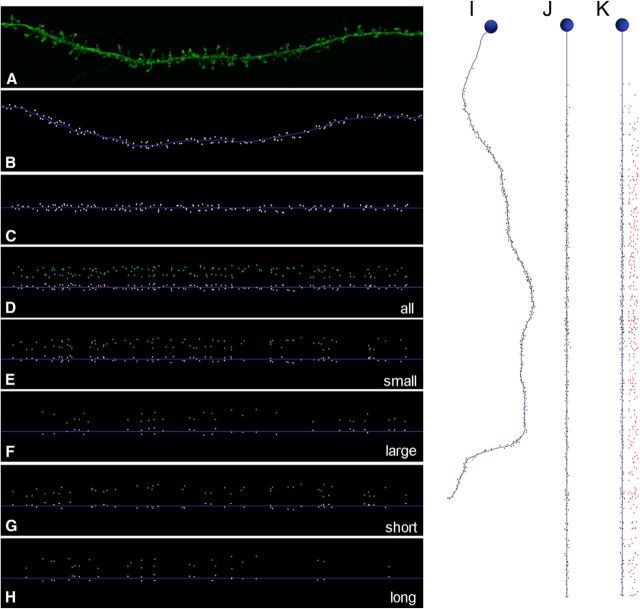
Figure 4.

Unstructured positioning of insertion points with different volume and lengths filters. A, Example of a basal dendritic segment. B, Insertion point of spines (white dots) in the same dendritic segment as in A. C, D, Straightening (C) and unrolling (D). E–H, Selective visualization of unfolded positioning of small (<0.3 μm³), large (>0.5 μm³), short (<1 μm), and long (>2 μm) spines using volume (E, F) and length (G, H) filters. I, Example of basal dendrite with insertion points of dendritic spines (black dots) along the distance from soma. J, K, Straightening (J) and unrolling (K) of I.

Spatial statistical analysis of spine distributions in whole-length basal dendrites

Finally, to explore whether dendritic segments had ordered spatial arrangement of spines at a larger spatial scale, we joined stacks of images containing the consecutive segments of each dendrite, from soma to the distal tip (Fig. 4I–K). Because apical dendrites were only partially captured, we performed visual analysis and the CSR tests only for basal dendrites (60 basal dendritic segments forming 19 entire dendrites). In only 1 of 19 complete dendrites, the null hypothesis of CSR was rejected. Furthermore, we used the same volume and shape filters that were applied above to specifically visualize particular populations of spines and tested the CSR null hypothesis for those combinations. The dataset consisted of 142 subsets of spines, and the null hypothesis CSR was not rejected in any case.

Discussion

Methodological considerations

The spatial distribution of spines along the dendrites, far from being a purely academic matter, could be very informative in revealing the overall structural and functional logic of brain circuits (Chklovskii et al., 2002; Yuste, 2011). In particular, Fourier analysis of spine distribution from Purkinje neurons from electric fish and mice indicates that spines are located along helical patterns, as if they were physically maximizing the connection probability of each spine with passing axons (O'Brien and Unwin, 2006).

In this study, we followed that pioneering work and examined whether spines in human neocortical pyramidal neurons are also placed along helical patterns on dendrites. To do so, we filled pyramidal neurons from different cortical areas, using lightly fixed autopsy material from adult human patients with unrelated pathologies and performed light microscopic 3D reconstruction of entire dendrites. We then used this database and performed using similar Fourier analysis as in (O'Brien and Unwin, 2006), and visually inspected >500 dendritic segments searching for potential helical patterns in the spatial Fourier transforms. We then selected the most promising samples and performed a complete reconstruction of the insertion point of every spine, applied straightening and unrolling preprocessing algorithms and then statistically analyzed the spatial distribution of spine insertion points, comparing them with a set of random CSR distributions generated artificially. This approach is in principle systematic, quantitative, and blind, but our methods also have shortcomings that the reader should be aware of, particularly when comparing our results with those of O'Brien and Unwin (2006). First, for apical dendrites, we focused mostly on spines located on the main dendritic trunks avoiding, for technical reasons, the distal fine branches. Second, postmorterm material could be subject to structural reorganization in the spines due to the death, something that we would not detect. Third, the fixation process could also alter the structure of the spines and bias our dataset toward more stable ones. Fourth, we assumed that the fluorescent dye filled the dendritic arbor completely but cannot rule out that there may be some spines that we could not visualize. Fifth, our analysis is based on confocal light microscopy reconstructions, and it is likely that it misses very small spines. From this point of view, volumetric reconstructions based on either electron microscopy or super-resolution optical techniques of living tissue could be used to rule out some of these potential problems. Finally, we report data from samples of only two individuals. Although we analyzed a large number of spines from many neurons and great care was taken to use identical experimental procedures and reconstruct similar neurons from the same cortical areas, the two patients differed in age and then it is impossible to ascertain whether our conclusions will hold with a similar analysis of a larger sample of individuals.

Lack of spatial structure in spine positioning in human cortical neurons

With these technical caveats, our main conclusion is our inability to detect clear evidence of spine helixes in these human cortical samples. Even though we cast a wide net analyzing spine distributions that differed according to age, cortical area, and spine size and morphology, we could account for the spatial distribution of most of our samples by assuming that they matched a random positioning principle. With very few exceptions, we could not reject the hypothesis that they follow a CSR distribution. We used artificially generated spine “helixes” to test the validity of our method, proving that spine helixes generate distributions that are statistically different from CSR ones, even when these artificial helixes were complex.

Our results not only rule out helixes but also discard other nonrandom distribution of spine positioning, at least for the samples analyzed. Our study contrasts with a recent analysis of the positions of dendritic spines in pyramidal neurons from Rhesus prefrontal cortex, reporting nonrandom clusters of spines in apical, albeit not oblique, dendrites (Yadav et al., 2012). Besides differences in species, cortical area, and methodology, in our study we unfortunately did not examine the distal branches of apical or oblique dendrites, so it is difficult to draw strong conclusions from this comparison. Because of this, we limit our conclusions to the species, ages, cortical areas, cell types, and dendrites studied. In addition, we should alert the reader that, on top of this spatial randomness at the microstructural level, in human neocortical pyramidal neurons (as well as in other species), spine distribution as a function of distance from the soma over a much larger spatial scales displays a proximal area of lower spine density along the apical/basal dendritic tree, followed by a plateau of high density that then slowly tapers gradually, as one moves away from the soma (Elston et al., 2001, 2005; Elston and DeFelipe, 2002; Ballesteros-Yáñez et al., 2006).

Implications for spine function

If spines are randomly positioned, the decision to generate a spine or not (and to build an excitatory synapse) likely occurs independently for every spine. Spatial randomness could be therefore a consequence of Peters' rule, where chance encountered between axons and dendrites determines the synaptic connectivity (Peters and Feldman 1976). Our results differ from those of O'Brien and Unwin (2006), and this could be due to many factors of which the cell type could be critical. Indeed, Purkinje cells have an intrinsic, cell autonomous spinogenesis (Sotelo, 1977, 1978), whereas pyramidal neuron spinogenesis is at least partly dependent on interaction with passing axons (Miller and Peters, 1981; Ziv and Smith, 1996; Yuste and Bonhoeffer, 2004). There could be also fundamental differences between species or developmental stages. In this respect, we only examined adult pyramidal neurons and that, given the amount of synaptic pruning found in the CNS (Ramón y Cajal, 1899; Rakic et al., 1986; Zuo et al., 2005), it is possible that, when spines are first formed during development, they could be positioned along helixes but that, after activity-dependent pruning no traces of these helixes maybe left in adult tissue. It would be interesting to study cortical samples from early developmental stages, in human or other species, and explore what is the spatial arrangement of the first complement of spines, before activity-dependent rules have had a chance to modify the circuit.