Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jul 24;4:5817. doi: 10.1038/srep05817

Crossover between Weak Antilocalization and Weak Localization of Bulk States in Ultrathin Bi2Se3 Films

Huichao Wang 1,2, Haiwen Liu 1,2, Cui-Zu Chang 3,4, Huakun Zuo 5, Yanfei Zhao 1,2, Yi Sun 1,2, Zhengcai Xia 5, Ke He 2,3,4,b, Xucun Ma 2,3,4, X C Xie 1,2, Qi-Kun Xue 2,3, Jian Wang 1,2,a
PMCID: PMC4108910  PMID: 25056600

Abstract

We report transport studies on the 5 nm thick Bi2Se3 topological insulator films which are grown via molecular beam epitaxy technique. The angle-resolved photoemission spectroscopy data show that the Fermi level of the system lies in the bulk conduction band above the Dirac point, suggesting important contribution of bulk states to the transport results. In particular, the crossover from weak antilocalization to weak localization in the bulk states is observed in the parallel magnetic field measurements up to 50 Tesla. The measured magneto-resistance exhibits interesting anisotropy with respect to the orientation of parallel magnetic field B// and the current I, signifying intrinsic spin-orbit coupling in the Bi2Se3 films. Our work directly shows the crossover of quantum interference effect in the bulk states from weak antilocalization to weak localization. It presents an important step toward a better understanding of the existing three-dimensional topological insulators and the potential applications of nano-scale topological insulator devices.

Topological insulators (TIs), a new type of quantum materials characterized by the existence of a gap in the energy spectrum and the symmetry-protected surface states within the bulk gap, have attracted significant interest in recent years1,2,3. As a result of the strong spin-orbit coupling (SOC), the spin-momentum locked surface states always show weak antilocalization (WAL) effect4,5,6 due to the acquired π Berry phase when completing a time-reversed self-crossing path. Plentiful interesting behaviors of TIs, particularly in the topologically protected surface states, have been explored through electrical transport experiments7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22. Whereas, it is known that the bulk states of the existing three-dimensional (3D) TIs are not perfectly insulating even at low temperatures, and as a direct consequence, the bulk states can also influence the transport behaviors of TIs. In order to develop a comprehensive understanding on the exotic properties of TIs, it is important to systematically study the transport of TIs taking into account the effects from the bulk states.

Contrasting to the symmetry protected surface states, the TI bulk states with strong SOC can lead to either WAL or weak localization (WL) depending on the experimental conditions5,6,23. Recently, the WL effect of bulk states has been studied in the ultrathin Bi2Se3 films under perpendicular magnetic field24. However, it is difficult to distinguish the bulk state features from the surface state behaviors by the perpendicular field transport measurements. In comparison, the parallel field magneto-resistance (MR) properties of TI films reveal more bulk-state information25,26, and therefore, the parallel magnetic field transport measurements provide a powerful tool in investigating the quantum interference effects in the TI bulk states.

Here we comprehensively study the transport properties of 5 quintuple layers (QLs) Bi2Se3 films grown on epi-ready α-Al2O3 (0001) substrates by molecular beam epitaxy (MBE). The in situ angle-resolved photoemission spectroscopy (ARPES) result shows that two quantum well states of the conduction band, as well as the surface states, contribute to the density of states near the Fermi level. The MR is measured in pulsed high magnetic field (PHMF) up to 50 Tesla (T). When the external field is perpendicular to the film plane, linear MR is observed above 16 T. In parallel magnetic field, MR behaviors of the TI films exhibit interesting anisotropy when the field orientation is tuned between B// ⊥ I and B// // I configurations. Specifically, while the field is increased up to 50 T, the MR always exhibits a distinctive switch from positive to negative when B// ⊥ I; whereas, when B// // I, such switch either occurs at a much larger field, or does not occur at all within 50 T. The theoretical analysis and the quantitative fitting for the experimental results indicate that such parallel field MR behaviors of the ultrathin TI films can be well explained using the WAL-WL crossover mechanism in the TI bulk states. To be specific, as a consequence of the strong SOC effect in the TI films, the phase coherence time τφ generally presents a larger time scale than the intrinsic spin-flip time τSO. As a result, the WAL effect always occurs when the magnetic field is relatively weak, whereas, the WL effect arises when the field becomes sufficiently strong. From this perspective, the MR switch from positive to negative can be understood as a manifestation of the WAL-WL crossover in the TI bulk states. In addition, we observe novel MR anisotropy with respect to the relative orientation of the parallel magnetic field and the current, which can be qualitatively explained using the SOC mechanism. Combining the ARPES data, the transport results and the theoretical analysis, we reveal the crossover of quantum interference effect, from WAL to WL, in the bulk states of the ultrathin Bi2Se3 films.

Results

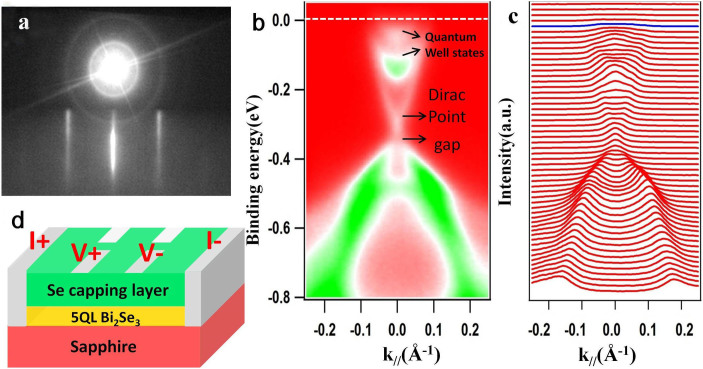
The 5 QLs Bi2Se3 films are epitaxially grown on sapphire (0001) substrates in an ultra-high vacuum MBE-ARPES-STM (scanning tunneling microscope) combined system27. Figure 1(a) shows the reflection high-energy electron diffraction (RHEED) pattern of a typical MBE-grown 5 QLs Bi2Se3 film, where the sharp 1 × 1 streaks demonstrate that the film has good single crystal quality. The band map of the film taken in Γ–K direction is shown in Figure 1(b). In the ARPES measurement, photoelectrons are excited by an unpolarized He-I light (21.21 eV), and collected by a Scienta SES-2002 analyzer. The topological surface states are observed within the bulk gap. A quite small gap is opened in the Dirac cone just below the Dirac point due to the coupling between the top and bottom surface states. Moreover, as shown in Figures 1(b) and (c), the quantum well states of the conduction band have a significant contribution to the Fermi surface. These observations indicate that our films are TIs with the Dirac surface states and the bulk states play a great role in the charge transport.

Figure 1. In situ characterizations of the 5QLs Bi2Se3 thin film grown by MBE and schematic structure for ex situ transport measurement.

Figure 1

Open in a new tab

(a) RHEED pattern with sharp 1 × 1 streaks. (b) ARPES band spectra along the Γ-Κ direction. The white dashed line indicates the Fermi level. The arrows label the quantum well states, the Dirac point and the small gap, respectively. (c) The corresponding momentum distribution curves of (b). The blue line indicates the Fermi level. (d) The schematic structure for transport measurements. The thickness is not to scale.

In order to explore the transport properties of the films by ex situ measurements, 20-nm-thick insulating amorphous Se is deposited on the TI films as a protection capping layer (Figure 1(d)). The Hall bars with channel dimensions of 600 × 400 μm2 are fabricated using standard photo-lithography method. An optical image of the typical Hall bar structure is shown in the inset of Figure 2(a). The transport properties of the films were measured mainly by using the standard four-electrode method in a 16 T Quantum Design PPMS (physical property measurement system) and PHMF at the Wuhan National High Magnetic Field Center. The non-destructive pulsed magnet has a rise time of 15 ms and fall time of 135 ms. The field and current directions are reversed in the measurements to improve the precision of the results by eliminating the parasitic voltages. Typical results from the sample 1 (a 5 QLs Bi2Se3 film) are shown in the main text. (The results are repeatable in a collection of samples.)

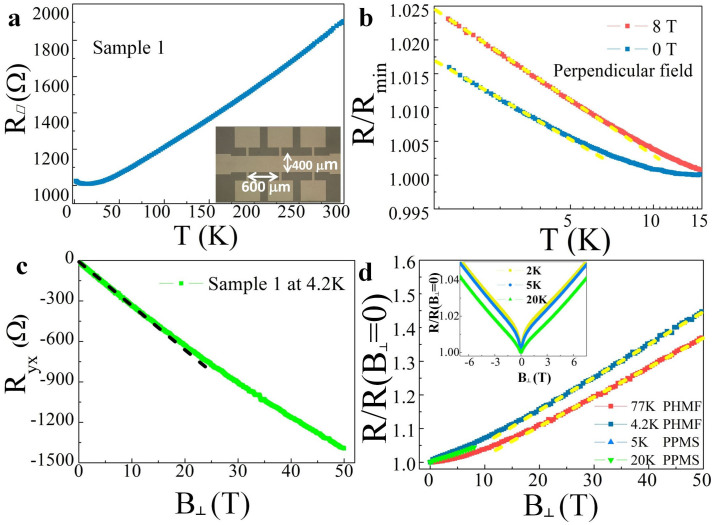
Figure 2. Transport properties of sample 1.

Figure 2

Open in a new tab

(a) The sheet resistance R□ versus temperature with an upturn in low temperature regime. The inset is an optical image of the Hall bar structure. (b) Normalized upturn resistances at fixed perpendicular fields. (c) Hall trace at 4.2 K in a magnetic field up to 50 T. (d) Normalized perpendicular field MR. The inset shows the MR dips around 0 T which are attributed to the WAL effect at low temperatures. The broken lines are guides to the eyes.

The dependence of the sheet longitudinal resistance R□ on the temperature was measured firstly (for the sample 1), which is shown in Figure 2(a). The resistance decreases almost linearly when the temperature decreases from 300 K to about 50 K. Whereas, when the temperature drops approximately below 12 K, the resistance develops an upturn. The upturn resistance, as shown in Figure 2(b), exhibits a logarithmic dependence on the temperature, which can be understood in terms of the quantum correction induced by the electron-electron interaction13. The resistance upturn becomes larger at 8 T than that at 0 T, which is due to the suppression of the WAL effect in the presence of the perpendicular magnetic field resulting in enhanced resistance. The Hall trace of the sample 1 at 4.2 K is shown in Figure 2(c). Utilizing the slope at low fields, we calculate the sheet carrier density ns ~ 1.89 × 1013 cm−2 and mobility μ ~ 316.6 cm2/(V·s) at 4.2 K.

Next, the MR behavior of the sample 1 at relatively low perpendicular fields (<16 T) was measured in PPMS and PHMF, respectively. The results in both measurements are consistent, which are shown in Figure 2(d). Specifically, these MR curves show typical dips around 0 T at low temperatures as a result of the WAL effect in TIs7,12,13,14,15, which can be clearly seen in the inset of Figure 2(d). In addition, a linear MR appears above 16 T at both 4.2 K and 77 K. This is consistent with the previous observation in a 5 QLs Bi2Se3 film grown on the same substrate by MBE15. Note that similar linear behavior of MR has been observed in many TI systems28,29,30,31,32,33,34,35, yet, the underlying origin remains to be clarified. Some attribute such linear MR to a quantum origin, including the Abrikosov's quantum linear MR model which relates the linear MR to the linear energy dispersion of the gapless topological surface states28,29,30, and the Hikami-Larkin-Nagaoka theory which interprets the linear-like MR at high fields in terms of the WAL mechanism31,32. Other theories associating the linear MR with a classical origin have also been proposed, such as the inhomogeneity model by Parish and Littlewood which stresses the influence from the sample inhomogeneity34,35.

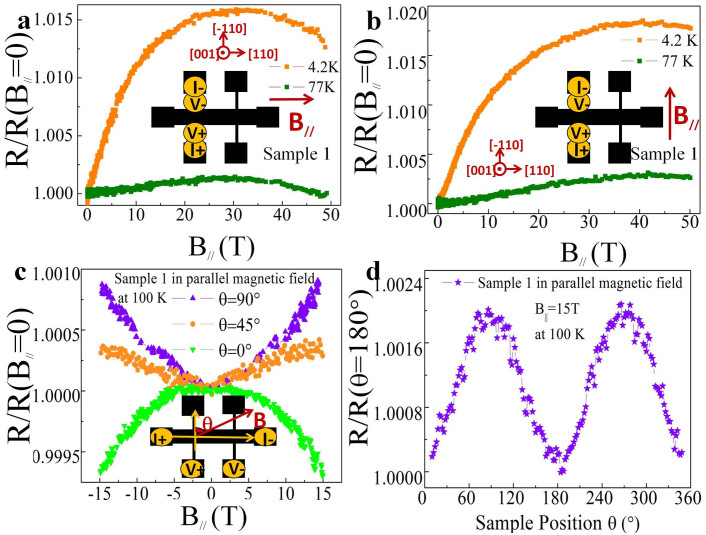
Interestingly, a different set of rich MR behavior is observed when a magnetic field parallel to the film plane is applied. In particular, as clearly shown in Figure 3, the normalized MR of sample 1 along the [110] direction in parallel field, exhibits a significant dependence on the relative orientation of B// and I. The behavior of MR when the parallel field is oriented along B// ⊥ I (the field increases up to 50 T) is shown in Figure 3(a). At 4.2 K, the MR first increases to a maximum at about 25 T, and then decreases as a downward parabolic-like curve. When the temperature is increased to 77 K, the MR slightly increases within 11 T and then decreases monotonically up to 50 T. In comparison, the MR behavior for the field orientation B// // I (Figure 3(b)) is different, only showing positive MR within 50 T at both 4.2 K and 77 K.

Figure 3. Normalized MR of sample 1 in parallel field along [110] direction.

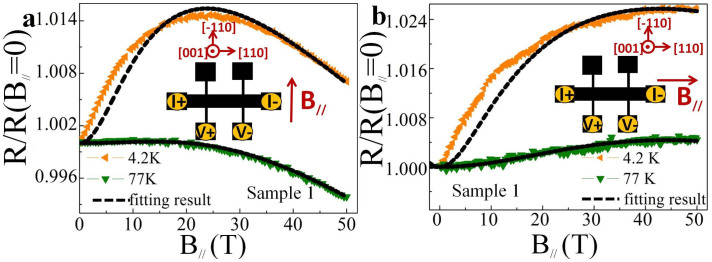
Figure 3

Open in a new tab

(a) B// ⊥ I and (b) B// // I. The triangles are experimental data and the black dashed lines are fitting curves by Equation (1). The MR behaviors can be well explained by the WAL-WL crossover mechanism in TI bulk states. The insets show the corresponding measurement configurations. [110] and [−110] are two different crystal directions along the film plane.

To further understand the parallel field MR behavior, we also measured the parallel field MR along the [−110] direction of the sample 1. The results are shown in Figures 4(a) and (b). The quasi-four-electrode method (insets of Figures 4(a) and (b)) is used only here due to the restriction of sample size. It is worth mentioning that such measurement method can introduce contact resistance that can lead to a weaker MR response without changing the curve shape (Supplementary Information). In this case, the MR switch from positive to negative is also clearly observed at 4.2 K and 77 K when B// ⊥ I, but much weaker when B// // I. For a fixed temperature, the switching field for B// // I is larger than that for B// ⊥ I. In order to explore the general dependence of the MR switch on the B//-I orientation, the parallel field MR of sample 1 with the current along the [110] direction under different position θ was measured (Figure 4(c)). The sample position θ refers to the angle between B// and the normal direction of I along the film plane (the inset of Figure 4(c)). Here θ = 0° means B// ⊥ I and θ = 90° means B// // I. When the magnetic field increases up to 16 T, the MR at 100 K increases when B// // I, but decreases when B// ⊥ I. When θ = 45°, the MR seems to show a competition between positive and negative MR. Normalized MR at 100 K as a function of θ when B// = 15 T is shown in Figure 4(d).

Figure 4. Control experiments with sample 1.

Figure 4

Open in a new tab

Normalized MR along [−110] direction when (a) B// ⊥ I and (b) B// // I. Normalized MR along [110] direction at 100 K when (c) θ = 0°, 45°, 90° and (d) θ continuously varies from 0° to 90°. θ = 0° means B// ⊥ I and θ = 90° means B// // I. The insets show the corresponding measurement configurations.

Discussion

A positive-to-negative MR switch of the ultrathin Bi2Se3 films is observed when the parallel magnetic field increases. The switch occurs in a broad range of temperature and exhibits anisotropy when the relative orientation of B// and I is varied. The parallel field MR data exhibit tiny variation in the presence of a large magnetic field, indicating a quantum correction regime. Taking into account the fact that the Fermi level locates at the bulk conduction band, and that the film shows quite large carrier density and lower mobility compared to those reported for the surface states of TI10, we conclude that the major contribution to the charge transport in our films comes from the bulk states instead of the surface states. We emphasize that, while similar negative MR behavior observed in Sn-doping Bi2Te3 films26 under parallel field was reported, a clear interpretation of the MR data and the comparison of different behaviors in Sn-doping samples are still missing. In contrast, for our present experimental results, the parallel field MR switch phenomenon of Bi2Se3 films can be well explained in terms of the quantum interference effects in the TI bulk states. In particular, as we shall describe in detail below, the positive and negative MR can be attributed to the presence of WAL and WL, respectively.

For a TI system with strong SOC, the correction to the MR behavior due to the effect of quantum interference6 is characterized by two time scales: the dephasing time τφ and the spin-flip time τSO. In the regime τφ ≫ τSO, the spin-orbit scattering is significant, which gives rise to frequent spin flips. As a result, the quantum interference between the time reversed trajectories is destructive, leading to the occurrence of WAL and a positive MR. In the regime where τφ is comparable to τSO or τφ < τSO, the spin-orbit scattering effect is weak and the scattering process barely affects the spin orientation. In such case, negative MR occurs with increasing magnetic field as a WL feature. In the intermediate regime where τφ > τSO, MR first increases to a peak value and then decreases, signifying a crossover from WAL to WL. Overall, the quantum interference behavior of a system is crucially dependent on the ratio between τφ and τSO.

In our thin films, the mean free path l can be estimated according to 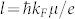Inline graphic, where kF can be obtained through the sheet density ns. For the sample 1 described here, l is approximately 20 nm, much larger than the thickness d = 5 nm. The parallel field transport thereby falls into the Dugaev-Khmelnitskii (DK) regime where the resistance change is given by36,37

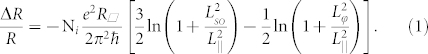graphic file with name srep05817-m1.jpg

Here ΔR = R(B) − R(B = 0). R can be regarded as the resistance in the absence of external magnetic field due to the quite small variation, and R□ is the sheet resistance. Ni is the number of channels contributing to the charge transport. In addition, three length scales are involved: Lso is the spin-flip length (the distance travelled by an electron before its spin direction is changed by the scattering, which depends on the strength of SOC in the bulk states. Please see Supplementary Information.), Lφ is the phase coherence length, and 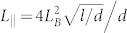Inline graphic with LB being the magnetic length 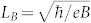Inline graphic. By varying only two fitting parameters Lφ and LSO, we present a quantitative fitting of the experimental data in Figure 3. In the case of B// ⊥ I, we have Lφ ≈ 140 nm, LSO ≈ 30 nm at 4.2 K and Lφ ≈ 40 nm, LSO ≈ 20 nm at 77 K. And for B// // I, Lφ ≈ 140 nm, LSO ≈ 18 nm at 4.2 K. Based on these fitting results, Lφ ≈ 40 nm and LSO ≈ 14 nm at 77 K when B// // I can be obtained by calculation (see Supplementary Information for details). Substituting these calculated values into Equation (1), we quantitatively reproduce the MR result at 77 K in B// // I configuration as shown in Figure 3(b). The tiny mismatches of the fitting MR curves may arise from the neglect of the electron-electron interaction13, which can actually play a role in the MR behavior.

It is noted that Ni = 2 in the fitting is identical to the number of bulk bands at the Fermi surface shown in Figure 2(b). While we cannot fully determine whether the two channels are completely from the two subbands of the bulk state or from the hybridized channels of bulk state and surface state, it is evident that the bulk state plays dominant role in the emergence of crossover behavior reported here. All the values of parameters shown above are fitting results and reasonable. The phase-coherence length Lφ decreases with temperature and Lφ is much larger than the mean free path as reported earlier15. Besides, the frequent scattering due to the edges in the ultrathin films makes Lso comparable to the mean free path. Based on the fitting results of experimental data, LSO is affected by the relative orientation of the parallel magnetic field and the current.

Through the parallel field MR curves of the ultrathin Bi2Se3 films, a clear image of the quantum interference effects with the WAL-WL crossover in the TI bulk states is depicted. Three cases are presented for the data in Figure 3 and 4. (I) For the B// ⊥ I configuration, the system usually falls into the intermediate regime (τφ > τSO) at relatively low temperatures. As a result, WAL effect characteristically arises when the field is weak, whereas, when the magnetic field becomes sufficiently large, a crossover into WL occurs. The data of Figure 3(a) and 4(a) belong to this case and the crossover is observed within 50 T. (II) For the B// // I configuration and relatively low temperatures, compared to (I), a weaker effect of the WAL-WL crossover is observed at a larger switching field due to a larger ratio τφ/τSO as shown in Figure 4(b). In Figure 3(b), only the WAL effect is observed at 4.2 K and 77 K. This may indicate that the switching fields from WAL to WL in both conditions are larger than 50 T. (III) For either of the two geometries, the MR may show only WL effect at high temperatures when τφ decreases and becomes comparable to τSO, even τφ < τSO. The θ = 0° data at 100 K in Figure 4(c) fall into this situation.

The observed anisotropy feature of MR can be related to many factors, including the band structure asymmetry, crystalline anisotropy, and the relative orientation of the parallel magnetic field and the current. However, generally speaking, both the band asymmetry and the crystal anisotropy could result in a MR behavior that varies along different crystal directions. Since the anisotropy of MR along the [−110] direction remains consistent with that of the [110] direction, we consider the relative directions of the parallel magnetic field and the current as the leading factor that contributes to the novel MR anisotropy reported here. The underlying physics can then be qualitatively understood in terms of the SOC mechanism. Consider a moving electron, which experiences an effective magnetic field Be that is perpendicular to the electron momentum. When B// ⊥ I, the main transport path of the electron is perpendicular to the external field, in which the spin-flip process due to the SOC effect is strongly suppressed by the external magnetic field, leading to an effectively larger τSO. In distinct contrast, when B// // I, the spin-flip process is hardly affected. This anisotropy in the effective SOC effect provides a mechanism that leads to the observed anisotropic MR here. Such explanation is also supported by Figures 4(c) and (d), which show an intimate relation between the parallel field MR and the sample position θ. Particularly, the negative MR behavior when B// ⊥ I is consistent with a larger effective τSO, while the positive MR when B// // I agrees with a smaller τSO. For arbitrary θ, the effective τSO is given by the combination of both effects, which leads to the MR-θ characteristics shown in Figure 4(d).

Interestingly, the anisotropy of the parallel field MR in thicker TI films (e.g. 45 QLs and 200 QLs Bi2Se3)38 seems to be opposite to the experimental results of the 5 QLs Bi2Se3 films. Additionally, there is one order of magnitude difference of the MR amplitudes for the thicker films38 between B//⊥I and B////I, while it is not the case for the results presented here. In light of many different factors between the thick and ultrathin films, such as the thickness and the weight of bulk states at the Fermi surface, we are not able to achieve a unified understanding. Further theoretical investigations in this context would be valuable towards a quantitative comprehension of the anisotropic parallel field MR of TI films in various field-current orientations.

In summary, the crossover from WAL to WL in TI bulk states is revealed clearly by the parallel field MR behaviors of the 5 QLs ultrathin Bi2Se3 films. The WAL-WL crossover is largely affected by the relative orientation of the parallel magnetic field and the current, which can be understood in terms of an orientation-dependent effective spin-flip time. To be specific, when B// ⊥ I, the MR within 50 T always exhibits the crossover at 4.2 K and 77 K, whereas, the crossover for B// // I occurs at a much higher magnetic field (possibly above 50 T), due to the anisotropic SOC effect under strong magnetic field. The novel transport properties of the ultrathin TI films demonstrated in this work are quite significant for a better understanding of the existing 3D TI materials and for the future potential magnetic applications of nano-scale TI devices.

Methods

Sample preparation

The high quality 5 QLs Bi2Se3 films studied here were grown on α-Al2O3 (sapphire) (0001) substrates in an ultra-high vacuum MBE-ARPES-STM combined system with a base pressure better than 2 × 10−10 mbar. Before sample growth, the sapphire substrates were first outgassed at 650°C for 90 min and then heated at 850°C for 30 min. High-purity Bi (99.9999%) and Se (99.999%) were evaporated from standard Knudsen cells. To reduce Se vacancies in Bi2Se3, the growth was kept in Se-rich condition with the substrate temperature at ~220°C. For the transport measurement, 20 nm Se was capped on the TI film as protection layer.

Device fabrication and measurement

Hall bar structure with channel dimensions of 600 × 400 μm2 was fabricated using standard photo-lithography method. Positive photoresist S1813 was spun at 4000 rpm for 45 seconds on Bi2Se3 film, followed by 110°C baking for 60 seconds. With a mask of Hall bar pattern, the photoresist-coated sample was exposed to ultraviolet light (365 nm wavelength) with exposure power of 8 mW/cm2 for 7 seconds. The exposed part of photoresist was removed after 40 seconds of developing (MFCD-26 developer). Then, bared area of Bi2Se3 film with no photoresist on was wet-etched with 1 g of potassium dichromate in 10 ml of sulfuric acid and 20 ml of DI water. The expected etch rate for Bi2Se3 was about 60 nm per minute, and DI water rinsing was needed. Via indium contacting, Au wires were attached as leads on samples at room temperature. Thus we were able to measure the transport properties of the fabricated devices by standard or quasi four-electrode method. Transport measurements were performed in PPMS (16T) and PHMF up to 50 T.

Author Contributions

J.W. and K.H. conceived and designed the study. H.W., Y.Z., Y.S. and J.W. carried on the transport measurements. C.C. did MBE growth and ARPES experiment. H.Z. and Z.X. helped in pulsed high magnetic field measurements. K.H., X.M. and Q.X. supervised the MBE growth and ARPES experiment. H.W., C.C., J.W., H.L. and X.C.X. analyzed the data. H.L. and X.C.X. did theoretical fittings. H.W., H.L. and J.W. wrote the manuscript.

Supplementary Material

Supplementary Information

Crossover supplementary

srep05817-s1.pdf (595.7KB, pdf)

Acknowledgments

We thank Liang Li for helpful discussions about the pulsed magnetic field measurements. This work was financially supported by the National Basic Research Program of China (Grant Nos. 2013CB934600 & 2012CB921300), the National Natural Science Foundation of China (Nos. 11222434 & 11174007), and the Research Fund for the Doctoral Program of Higher Education (RFDP) of China.

References

  1. Qi X.-L. & Zhang S.-C. The quantum spin Hall effect and topological insulators. Phys. Today 63, 33–38 (2010). [Google Scholar]
  2. Hasan M. Z. & Kane C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010). [Google Scholar]
  3. Qi X.-L. & Zhang S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011). [Google Scholar]
  4. Lu H.-Z., Shi J. R. & Shen S.-Q. Competition between weak localization and antilocalization in topological surface states. Phys. Rev. Lett. 107, 076801 (2011). [DOI] [PubMed] [Google Scholar]
  5. Hikami S., Larkin A. I. & Nagaoka Y. Spin-orbit interaction and magnetoresistnce in the two dimensional random system. Prog. Theor. Phys. 63, 707–710 (1980). [Google Scholar]
  6. Bergmann G. Weak localization in thin films: a time-of-flight experiment with conduction electrons. Phys. Rep. 107, 1–58 (1984). [Google Scholar]
  7. Checkelsky J. G. et al. Quantum interference in macroscopic crystals of nonmetallic Bi2Se3. Phys. Rev. Lett. 103, 246601 (2009). [DOI] [PubMed] [Google Scholar]
  8. Taskin A. A. & Ando Y. Quantum oscillations in a topological insulator Bi1−xSbx. Phys. Rev. B 80, 085303 (2009). [Google Scholar]
  9. Eto K., Ren Z., Taskin A. A., Segawa K. & Ando Y. Angular-dependent oscillations of the magnetoresistance in Bi2Se3 due to the three-dimensional bulk Fermi surface. Phys. Rev. B 81, 195309 (2010). [Google Scholar]
  10. Qu D.-X., Hor Y. S., Xiong J., Cava R. J. & Ong N. P. Quantum oscillations and Hall anomaly of surface states in the topological insulator Bi2Te3. Science 329, 821–824 (2010). [DOI] [PubMed] [Google Scholar]
  11. Peng H. et al. Aharonov–Bohm interference in topological insulator nanoribbons. Nat. Mater. 9, 225–229 (2010). [DOI] [PubMed] [Google Scholar]
  12. Chen J. et al. Gate-voltage control of chemical potential and weak antilocalization in Bi2Se3. Phys. Rev. Lett. 105, 176602 (2010). [DOI] [PubMed] [Google Scholar]
  13. Wang J. et al. Evidence for electron-electron interaction in topological insulator thin films. Phys. Rev. B 83, 245438 (2011). [Google Scholar]
  14. He H.-T. et al. Impurity effect on weak antilocalization in the topological insulator Bi2Te3. Phys. Rev. Lett. 106, 166805 (2011). [DOI] [PubMed] [Google Scholar]
  15. Liu M. H. et al. Electron interaction-driven insulating ground state in Bi2Se3 topological insulators in the two-dimensional limit. Phys. Rev. B 83, 165440 (2011). [Google Scholar]
  16. Steinberg H., Gardner D. R., Lee Y. S. & Jarillo-Herrero P. Surface state transport and ambipolar electric field effect in Bi2Se3 nanodevices. Nano Lett. 10, 5032–5036 (2010). [DOI] [PubMed] [Google Scholar]
  17. Yuan H. T. et al. Liquid-gated ambipolar transport in ultrathin films of a topological insulator Bi2Te3. Nano Lett. 11, 2601–2605 (2011). [DOI] [PubMed] [Google Scholar]
  18. Wang Y. et al. Gate-controlled surface conduction in Na-doped Bi2Te3 topological insulator nanoplates. Nano Lett. 12, 1170–1175 (2012). [DOI] [PubMed] [Google Scholar]
  19. Fang L. et al. Catalyst-free growth of millimeter-long topological insulator Bi2Se3 nanoribbons and the observation of the π-Berry phase. Nano Lett. 12, 6164–6169 (2012). [DOI] [PubMed] [Google Scholar]
  20. Tian M. L. et al. Dual evidence of surface Dirac states in thin cylindrical topological insulator Bi2Te3 nanowires. Sci. Rep. 3, 1212 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Yan Y. et al. Synthesis and quantum transport properties of Bi2Se3 topological insulator nanostructures. Sci. Rep. 3, 1264 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Zhao Y. F. et al. Demonstration of surface transport in a hybrid Bi2Se3/Bi2Te3 heterostructure. Sci. Rep. 3, 3060 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Lu H.-Z. & Shen S.-Q. Weak localization of bulk channels in topological insulator thin films. Phys. Rev. B 84, 125138 (2011). [Google Scholar]
  24. Zhang L. et al. Weak localization effects as evidence for bulk quantization in Bi2Se3 thin films. Phys. Rev. B 88, 121103(R) (2013). [Google Scholar]
  25. Lin C. J. et al. Parallel field magnetoresistance in topological insulator thin films. Phys. Rev. B 88, 041307(R) (2013). [Google Scholar]
  26. Zhang H. B. et al. Weak localization bulk state in a topological insulator Bi2Te3 film. Phys. Rev. B 86, 075102 (2012). [Google Scholar]
  27. Chang C.-Z. et al. Growth of quantum well films of topological insulator Bi2Se3 on insulating substrate. Spin 1, 21–25 (2011). [Google Scholar]
  28. Tang H., Liang D., Qiu R. L. J. & Gao X. P. A. Two-dimensional transport-induced linear magneto-resistance in topological insulator Bi2Se3 nanoribbons. ACS Nano. 5, 7510–7516 (2011). [DOI] [PubMed] [Google Scholar]
  29. He H. T. et al. High-field linear magneto-resistance in topological insulator Bi2Se3 thin films. Appl. Phys. Lett. 100, 032105 (2012). [Google Scholar]
  30. Gao B. F. Gehring P., Burghard M. & Kern K. Gate-controlled linear magnetoresistance in thin Bi2Se3 sheets. Appl. Phys. Lett. 100, 212402 (2012). [Google Scholar]
  31. Zhang S. X. et al. Magneto-resistance up to 60 Tesla in topological insulator Bi2Te3 thin films. Appl. Phys. Lett. 101, 202403 (2012). [Google Scholar]
  32. Assaf B. A. et al. Linear magnetoresistance in topological insulators: Quantum phase coherence effects at high temperatures. Appl. Phys. Lett. 102, 012102 (2013). [Google Scholar]
  33. Wang C. M. & Lei X. L. Linear magnetoresistance on the topological surface. Phys. Rev. B 86, 035442 (2012). [Google Scholar]
  34. He X. Y. et al. Highly tunable electron transport in epitaxial topological insulator (Bi1−xSbx)2Te3 thin films. Appl. Phys. Lett. 101, 123111 (2012). [Google Scholar]
  35. Tian J. et al. Quantum and classical magnetoresistance in ambipolar topological insulator transistors with gate-tunable bulk and surface conduction. Sci. Rep. 4, 4859 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Altshuler B. L., Aronov A. G., Khmelnitskii D. E. & Larkin A. I. in Quantum Theory of Solids, edited by Lifshitz, I. M. (Mir Publishers, Moscow, 1982). [Google Scholar]
  37. Dugaev V. K. & Khmelnitskii D. E. Magnetoresistance of metallic films with low impurity concentration in a parallel magnetic field. Sov. Phys. JETP 59, 1038–1041 (1984). [Google Scholar]
  38. Wang J. et al. Anomalous anisotropic magnetoresistance in topological insulator films. Nano Res. 5, 739–746 (2012). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Crossover supplementary

srep05817-s1.pdf (595.7KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES