A Telerobotic System for Transnasal Surgery

Abstract

Mechanics-based models of concentric tube continuum robots have recently achieved a level of sophistication that makes it possible to begin to apply these robots to a variety of real-world clinical scenarios. Endonasal skull base surgery is one such application, where their small diameter and tentacle like dexterity are particularly advantageous. In this paper we provide the medical motivation for an endonasal surgical robot featuring concentric tube manipulators, and describe our model-based design and teleoperation methods, as well as a complete system incorporating image-guidance. Experimental demonstrations using a laparoscopic training task, a cadaver reachability study, and a phantom tumor resection experiment illustrate that both novice and expert users can effectively teleoperate the system, and that skull base surgeons can use the robot to achieve their objectives in a realistic surgical scenario.

I. Introduction

At some time in their lives, 1 in 5 people will have a pituitary tumor, and 1 in 120 of these will have the tumor grow large enough (>1 cm in diameter) that surgi­cal resection is needed [1]. Traditionally, surgery to remove pituitary tumors and other tumors at the skull base requires transcranial or transfacial access. In these approaches, large, traumatic openings must be created in the patient's forehead (followed by brain retraction) or cheek (leading to disfigurement). Endonasal skull base surgery reduces invasiveness (Fig. 1), resulting in less trauma, fewer complications, and shorter surgical durations [2], [3]. However, despite these compelling advantages for the patient, only a small percentage of skull base surgeries are done endonasally. One can infer from [4]–[6] that this number is certainly less than 50% and most likely below 20%, though exact statistics are not available in the clinical literature.

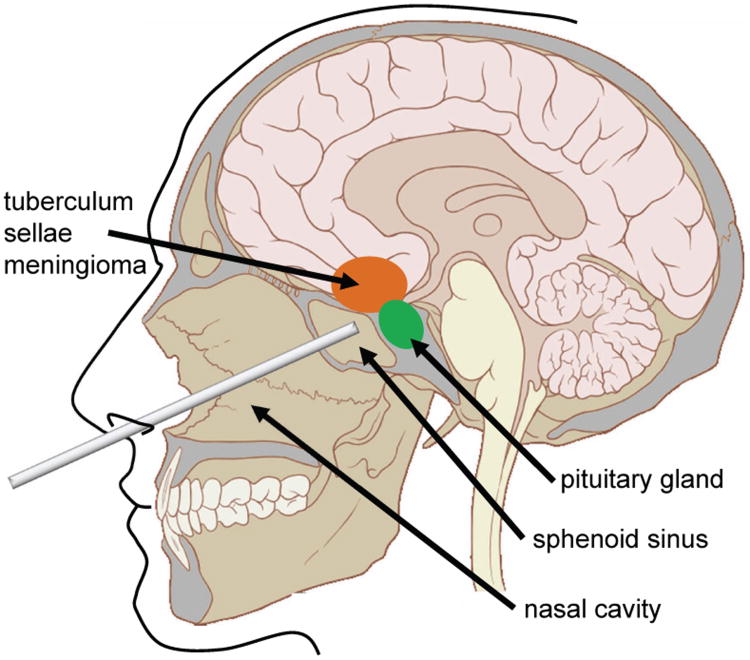
Fig. 1.

An illustration of the endonasal approach to the pituitary gland using a straight tool. The nasal cavity must be prepared by initial drilling to gain access through the sphenoid sinus. In the longer term, curved instruments may help surgeons reach other locations at the skull base including the tuberculum sella, which is nearly inaccessible endonasally today [12].

This endonasal approach is not deployed more frequently despite its demonstrated benefits to the patient because existing surgical instruments have limited dexterity and approach angles [7], [8], and simultaneously manipulating several of them through a nostril while performing complex surgical procedures is so technically challenging that only a small number of expert surgeons can accomplish it [9]. Even for these experts, mortality rates remain non-negligible (0.9% [10]), and there remain many contraindications for the endonasal approach, including occlusion of the surgical site by delicate neurovascular structures (e.g. carotid arteries, optic nerves), inability to fully reconstruct the dura due to lack of tool dexterity, and long surgery duration [2], [11]. All these contraindications are directly related to limitations in instrument dexterity and visualization, which motivates the development of the robotic system we describe in this paper. Such a robot can potentially increase surgical dexterity and reduce the technical complexity of the procedure for surgeons, thereby increasing the percentage of patients who benefit from the endonasal approach.

A. Related Work

While many robotic systems have been developed for intravascular interventions (e.g. the robot discussed in [13]), as well as natural orifice surgery through other body orifices (e.g. [14] [15] [16]), or single abdominal ports (e.g. [17] [18] [19]), comparatively few systems targeted endonasal surgery. This is likely due to the smaller size of the nostril compared to other natural orifices (e.g. the throat, single abdominal port, etc.). The few endonasal robotic systems that do exist are best considered in terms of their function within the entire surgical workflow.

The workflow of endonasal surgery is as follows: Surgery begins with widening of the nasal passage as necessary, to permit access to the anterior wall of the sphenoid sinus. Then, under endoscopic visualization (Fig. 1 illustrates the location of the endoscope), the sphenoid sinus is exposed by removing the anterior wall, followed by drilling of the posterior wall, providing access to the tumor. The surgeon then resects the tumor using hand-held tools with straight shafts. Though a variety of end-effector designs are possible on these hand-held tools, curettes (rings of metal for scraping away tumor material) are used most often and most extensively. Since pituitary tumors are very soft (similar in consistency to brain tissue), and these rings are thin, yet not particularly sharp, they are useful for scraping away tumor tissue while sparing blood vessels or nerves they may inadvertently contact. Image-guidance systems are also usually employed during the surgery. These systems (e.g. BrainLab AG, Medtronic Inc.) allow registration of intraoperative anatomy and tool positions with preoperative medical images. Prior robots developed for endonasal surgery have been used to ensure safety during the initial bone drilling operations needed to expose the surgical site [20], [21]. Robots have also been used to assist in endoscope manipulation [22], [23], and a 4 mm continuum robot has been developed to steer a camera in the sinus cavity for visual inspection [24].

For endonasal robots, the limited space available in the nostril opening, combined with the need to work dexterously within the cavities in the head, implies that instrument shafts must be small in diameter while enabling dexterous motions of the instrument tips. A recently invented robot design that matches these characteristics is the concentric tube robot concept (Fig. 2), which is also known by the name active cannula [25], [26]. Mechanics-based models of these robots have been developed over the past several years (see [25] and [26], and references therein), and the latest models can describe the shape of the device for the general case of arbitrarily many tubes, with arbitrary precurvatures, in the presence of arbitrary external loading. These advanced models lay the foundation for adaptation of concentric tube robots to specific surgical procedures, and progress has been made in applications including cardiac surgery [27], neurosurgery [28], lung interventions [29], and endonasal surgery [30], which is the focus of this paper.

Fig. 2.

An example 3-tube concentric-tube robot. The line drawing inset illustrates the 2n actuatable degrees of freedom for an n tube robot.

B. Contributions

Our current system is unique among robotic systems pre­viously proposed for endonasal surgery [20]–[22], [24] and complements them by providing a novel way to resect tumors and dexterously manipulate tissues after surgical site exposure. To elaborate upon this, a single endonasal surgery could potentially make use of our system while also using all previously suggested robotic approaches for other aspects of the overall surgical procedure. Such a hypothetical surgery would begin with virtual fixture-assisted drilling [20], [21] followed by use of robot-controlled cameras [22], [24] to provide visualization of the end-effectors of the system described in this paper, as the surgeon uses them to resect a skull base tumor.

In this paper, we provide an archival unification of multiple results previously presented in preliminary form at conferences [30]–[32]. Contributions include a description of how clinical considerations informed the design process for our image-guided surgical robot system, computation of the manipulator Jacobian for a concentric tube manipulator using the latest mechanics-based models, a method for using this Jacobian to enable teleoperation, and demonstration of use of the robot to resect anthropomorphic tumor phantoms placed in a cadaver skull. Additional contributions in this manuscript beyond the scope of previous conference publications include computational advancements enabling the model and Jacobian to be computed efficiently enough for real-time control, experiments demonstrating the ability of both surgeons and novice users to complete a laparoscopic training task, and experiments verifying that surgeons can reach anatomical features of interest in skull base surgery in a cadaver using the system.

II. Concentric-Tube Robot Kinematics

In this section we provide a concise review of the previously validated mechanics-based model for the forward kinematics and deflection under loads of a concentric-tube manipulator with n tubes [26]. The inputs to the model consist of a vector q = [α₁,…α_n, β₁, …β_n]^T containing the 2n actuation variables (the angular and translational positions of each tube base, α_i and β_i, respectively), as well as external loads applied.

The output of the model is an arc length parametrized homogeneous transformation g(s) ∈ SE(3) consisting of a rotation matrix R₁(s) ∈ SO(3) and vector p₁(s) ∈ ℝ³ which describe the position and material orientation of the centroidal axis of the device (or more specifically, of the longest and innermost tube, tube 1).

The model itself may be derived from either Cosserat rod theory or from energy methods, and it ultimately consists of a multi-point boundary value problem on a nonlinear set of ordinary differential equations. The general model in [26], [31] is written below for the special case of tubes with piecewise-constant precurvature functions (e.g. ${\mathit{u}}_i^{\ast }={\left[\begin{array}{lll}{k}_i& 0& 0\end{array}\right]}^T$ where k_i is the curvature of tube i, which is zero in sections where tube i is straight), with a point force F and moment L applied at the end-effector. In this case, the model differential equations are written as follows:

$$\begin{array}{l}{\dot{\mathit{p}}}_1=R_1{\mathit{e}}_3\\ {\dot{R}}_1=R_1{\widehat{\mathit{u}}}_1\\ {\dot{\theta }}_i=u_{iz}-u_{1z}\text{for}i=2\dots n\\ {\dot{u}}_{iz}=-\frac{k_i{E}_i{I}_i}{G_i{J}_i}{u}_{iy}\text{for}i=1\dots n\\ {\dot{\mathit{m}}}_{1xy}={(-{\widehat{\mathit{u}}}_1{\mathit{m}}_1-{\widehat{e}}_3{R}_1^T\mathit{F})}_{xy}\end{array}$$ (1)

where m₁(s) is the total internal moment vector carried by the collection of tubes, expressed in R₁ coordinates, and F is expressed in global coordinates for the i^th tube, E_i is Young's modulus, I_i is the second area moment of tube cross section, G_i is the shear modulus, u_i is the curvature vector, θ_i is the axial rotation of the tube relative to tube 1, e₁, e₂, and e₃ are the standard basis for ℝ³. Here, the dot represents a derivative with respect to the arc length along the robot (s ∈ [0,ℓ₁], where s = 0 corresponds to a fixed entry point at the robot base, and ℓ₁ corresponds to the tip of the manipulator), and the ^ denotes conversion of a vector in ℝ³ to a skew-symmetric matrix, as defined in [33].

Intermediate equations needed to compute (1) are:

$$\begin{array}{l}{m}_{1z}=\sum _{i=1}^n{G}_i{J}_i{u}_{iz},\\ {\mathit{u}}_{1xy}=\frac{1}{EI}({\mathit{m}}_{1xy}+\sum _{i=1}^n[\begin{array}{l}cos{\theta }_i\\ sin{\theta }_i\end{array}]E_j{I}_j{k}_j),\\ {\mathit{u}}_{iy}=\left[\begin{array}{ll}sin{\theta }_i& cos{\theta }_i\end{array}\right]{\mathit{u}}_{1xy}.\end{array}$$ (2)

Initial conditions (at s = 0) are known for some of the variables and are specified below:

$$\begin{array}{l}{\mathit{p}}_1(0)={[\begin{array}{lll}0& 0& 0\end{array}]}^T,\\ R_1(0)=\left[\begin{array}{lll}cos({\alpha }_1-{\beta }_1{u}_{1z}(0))& -sin({\alpha }_1-{\beta }_1{u}_{1z}(0))& 0\\ sin({\alpha }_1-{\beta }_1{u}_{1z}(0))& cos({\alpha }_1-{\beta }_1{u}_{1z}(0))& 0\\ 0& 0& 1\end{array}\right],\\ {\theta }_i(0)={\alpha }_i-{\alpha }_1-({\beta }_i{u}_{iz}(0)-{\beta }_1{u}_{1z}(0)).\end{array}$$ (3)

The boundary conditions at the ends of tubes are:

$$\begin{array}{l}{G}_1{J}_1{u}_{1z}({\ell }_1)-{\mathit{e}}_3^T{R}_1^T\mathit{L}=0\\ G_i{J}_i{u}_{iz}({\ell }_i)=0,\text{for}i=2\dots n\\ {\mathit{m}}_{1xy}({\ell }_1)-{\left(R_1^T\mathit{L}\right)}_{xy}=0,\end{array}$$ (4)

where L is expressed in global coordinates.

III. Endonasal Robot System Design

Our robotic system for endonasal surgery (Fig. 3) incorporates two concentric tube manipulators, which can be teleoperated via haptic devices under endoscopic visualization. In this section we address our design methodology for this robot, before proceeding to control, image-guidance, and user studies in subsequent sections.

Fig. 3.

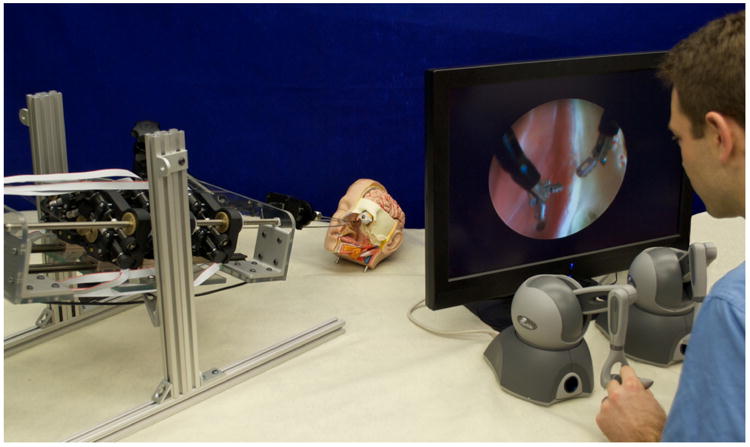
Prototype robot system for transnasal surgery at the skull base. The robot (on the left) actuates two cannulas composed of three tubes each. The cannulas are inserted through the nostril of an anatomical head model. For visualization of the surgical site, an endoscope is held in place by a passive arm. The master console (on the right) shows the endoscope view to the operator. Teleoperation is realized using two haptic input devices.

A. Workspace Characterization

At Vanderbilt University Medical Center, endonasal skull base surgery is typically performed through a single nostril. To characterize the workspace available in pituitary surgery, we manually segmented preoperative computed-tomography (CT) images of an average adult skull base surgery patient. The resulting intranasal space available is shown in Fig. 4, and consists of a nostril opening with dimensions 16×35 mm followed by a passage that widens as it approaches the pituitary gland at the rear of the workspace. The distance from the nostril entrance to the pituitary is about 100 mm. The sella turcica (chamber holding the pituitary gland) in a healthy patient is roughly ellipsoidal with a 8.5 mm major radius and 6 mm minor radius, but is typically much larger in patients with a pituitary tumor.

Fig. 4.

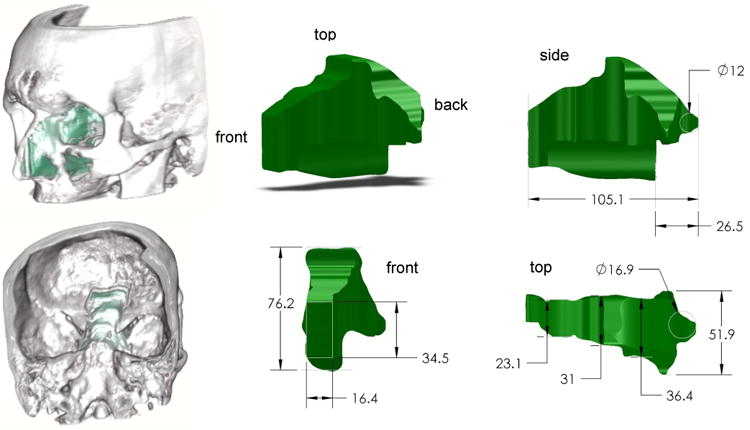
Maximum surgical workspace through a single nostril for endonasal skull base surgery for an average sized human. All dimensions in mm.

B. Concentric Tube Manipulator Design

Concentric tube continuum robots offer a large design space for application-specific customization [27], [28], [30]. Variables that can be selected by the designer include the number of tubes used and the shape of each tube (general space curves can be pre-set into nitinol by a heat treatment process). Tube diameters and wall thicknesses can also be selected to suit end effectors or instruments carried through the central working channel, and also to design the overall stiffness of the robot in various configurations.

Research on customization of concentric tube robots is still in its early stages [27], [28], [30]. Initial approaches have all begun by restricting the design space to a subset of the total space available (e.g. choosing a fixed number of tubes a priori, assuming constant curvature, etc.) to simplify the design problem. Additionally, to speed computation, initial approaches have used simplified models, either using constant curvature arcs (no mechanics-based model) [28], or by using a model that neglects torsional compliance [27]. Similar to prior approaches, in this paper we also make initial choices restricting the space of possible designs to a specific number of tubes and assume straight transmissions followed by sections of constant curvature. However, we use the full mechanics-based model given in Section II, which is desirable because it is known to more accurately represent the shape of the real, physical robot [34]. Another difference between our approach and prior approaches is that we design for reachability over a volume rather than for specific points.

We began the design process by restricting the family of possible individual tube curvatures to those curves with an initial straight section followed by a section of constant curvature at their tips. Next, we defined a concentric tube robot design d as a vector of 3n parameters where n is the number of component tubes. Each component tube i with i ∈ {1,…, n} is described by three parameters: i.e. length of the straight section $L_i^s$, length of the curved section $L_i^c$, and the constant curvature of the curved section κ_i. We restrict our design space to n = 3 tubes and further define the outermost tube to be straight with a length of 100 mm.

The objective of our component tube optimization (Algorithm 1) is to find a design that covers the surgical workspace within the target region, i.e. the pituitary gland approximated by an ellipsoid E as described previously. To determine coverage of E, we discretized the configuration space q of the concentric tube manipulator in 3 mm translational and 45 ° rotational steps and ran the robot model for each combination of discrete actuator values. We then determined the percentage of the ellipsoid covered by a component tube design d as the fraction of volume of the convex hull of all robot tip positions within E and the volume of E. Algorithm 1 describes our objective function in pseudo-code notation. To determine the optimal design d∗, we apply a heuristic search method for minimization of the objective function that uses the Nelder-Mead simplex algorithm, implemented in Matlab using fminsearch.

Algorithm 1 Objective Function f(d) for optimal component tube design

Input:

d: component tube design

a, b, c: radii of ellipsoid E

[x0, y0, z0]T: position of E

VE = (4/3)πabc: Volume of E

Output:

c: uncovered percentage of E for d

list = {} for all discrete actuator positions q do p ← ForwardKinematics(q,d) if $({(\frac{p(x)-x_0}{a})}^2+{(\frac{p(y)-y_0}{b})}^2+{(\frac{p(z)-z_0}{c})}^2)\le 1$ then list.append(p) end if end for VC ← V( ConvexHull (list)) return $1-\frac{V_C}{V_E}$

We applied this optimization method using both a simplified kinematics model assuming the component tubes to be torsion-ally rigid (as reported in [30]), and the full mechanics-based model described in Section II. We determined the component tube parameters in Table I using this approach. The outer diameter (OD) and inner diameter (ID) of the tubes (and thus their stiffnesss) were not part of the optimization and were selected to match the parameters of the physical tubes used in our robot prototype described later. In terms of runtime, the optimization using the torsionless model took about 2.5 min, while the optimization using the mechanics-based model took about 36 h. In both cases, the determination of the configuration space was parallelized on a quad core Intel Core i7 system with 3.4 GHz. We note that while these results are a promising step forward, tube design cannot be considered a solved problem for a variety of reasons, and direct the reader to further comments on this topic in Section VI.

Table I. Optimized Tube Parameters. All Values in mm, κ in mm⁻¹.

Model	torsionless			mechanics-based
Tube	Outer	middle	inner	outer	middle	inner
$L_i^s$	100	119.9	165.1	100	112.3	201.6
$L_i^c$	0	63.1	60.0	0	68.1	74.8
κ	0	0.0083	0.0182	0	0.0109	0.0128
OD	2.32	1.68	1.17	2.32	1.68	1.17
ID	1.87	1.35	0.76	1.87	1.35	0.76

C. Actuation Unit Design

Each component tube is actuated by an individual carrier which grasps the tube at its base and contains two encoded motors (RE 339152, Maxon Inc., Switzerland). On a given carrier, translation is accomplished by one motor using a worm gear to spin a nut that rides on a stationary lead screw. The rotation mechanism on a given carrier also uses a worm gear to spin the spring collet used to grasp the base of its respective tube. Use of a collet closure system permits easy replacement of tubes or changes in tube diameters as needed.

The carriers are affixed to a frelon self-lubricating guide block that rides on an aluminum guide rail. For each three-tube active cannula, three carriers ride on a single guide rail, making up one actuation module. In this design, we have mirrored two modules and placed them next to each other. The modules are affixed to a positioning stage built from aluminum profiles (80/20 Inc., USA). Each actuation module is controlled by a separate control board (DMC-4080, Galil, USA) that provides low level PID control and amplification, and enables interfacing via Ethernet.

D. End-effectors

We outfitted our concentric tube manipulators with both gripper and curette end-effectors (Fig. 6). To create the gripper, we disassembled a flexible grasper (Endo-Jaw, FB-211K, Olympus, Japan) by removing its outer sheath and inserting the gripper control wires through the innermost tube of the concentric tube manipulator. The gripper jaws have a length of 4mm and an opening angle of 110°. The diameter of the stainless steel forceps is 1.4 mm. The diameter of the closed gripper is 1.75 mm. For the curette end-effector, we custom built a ring by bending a steel ribbon into an ellipse (major radius 2 mm, minor radius 1.75 mm) and a height of 1.15 mm. The ring is affixed to a tube which is then glued into the innermost tube of the concentric tube manipulator.

Fig. 6.

End-effectors: Ring curette (left) and gripper (right).

E. Cadaver Setup Trial

To verify the feasibility using a robot of this type in endonasal surgery, we performed a preliminary trial in a human cadaver head. The nasal passages were surgically prepared, the sphenoid sinus exposed, and the anterior wall removed to expose the pituitary gland, as is typically done in clinical practice. The head was placed on an operating table in the typical position used in endonasal surgery. The robot was placed on the operating table at a relative angle of approximately 45° with respect to the bed upon which the head rested. Note that in an eventual clinical system we envision the robot being suspended over the patient on a positioning arm. This arm would replace the support rails visible at the bottom of the robot in Fig. 5. In this setup trial we simply placed these rails on the hospital bed as shown in Fig. 7. A straight endoscope was used for visualization, inserted through one nostril, and manually operated by the surgeon. Both robotic manipulators were inserted through the other nostril. In this way we verified that robot manipulators could reach the pituitary gland. Figure 7 shows the experimental setup and an endoscopic view onto the pituitary gland.

Fig. 5.

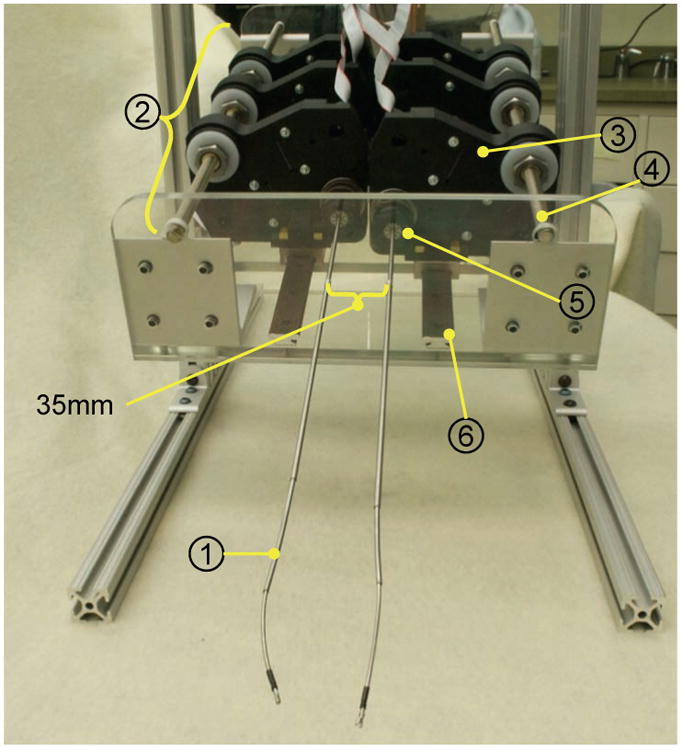
Prototype bimanual active cannula robot. (1) Active cannula gripper end-effector. (2) Actuation module for one cannula. (3) C associated with one tube. (4) Lead screw for translation of the ca (5) Collet closure for grasping one tube. (6) Guide rail.

Fig. 7.

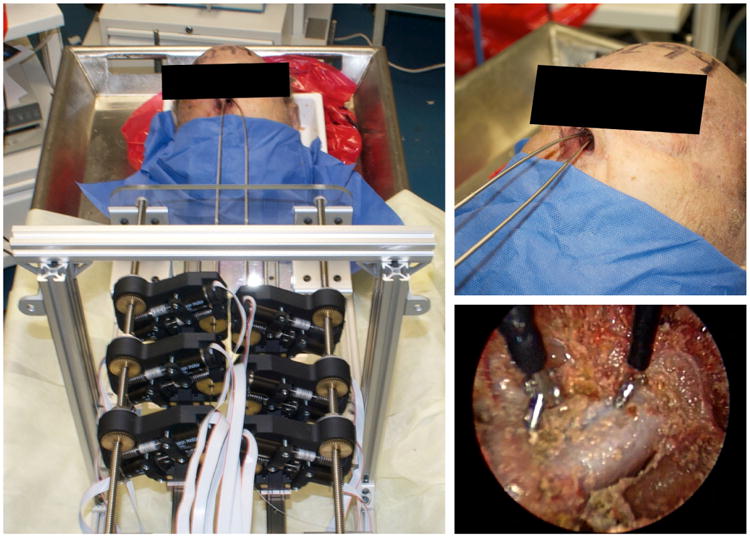
(Left) Setup trial of transnasal skull base surgery robot system in a human cadaver head. (Upper Right) Two concentric tube robot manipulators enter the nasal passage through a single nostril. (Lower Right) Endoscope view on the two gripper end-effectors facing the pituitary gland.

IV. Robot Control

A. Efficient Model Computation

We numerically solve the model of Section II by employing an explicit forward integration scheme (fourth-order Runge-Kutta) and using a shooting method to converge on the correct values for the unspecified initial conditions. We define a vector ${\mathit{y}}_u(0)={[u_{1z}(0),\dots ,u_{nz}(0),{\mathit{m}}_{xy}^{1T}(0)]}^T$ containing these unspecified initial conditions, and a vector b containing the boundary condition residuals (the left-hand sides of (4)) which result from the solution of the initial value problem for a particular guess of y_u(0). The gradients of the boundary condition residuals with respect to the unspecified initial conditions are contained in a matrix $B_u=\frac{\partial \mathit{b}}{\partial {\mathit{y}}_u(0)},$ which we compute by numerically integrating its arc-length derivative (which is obtained analytically, as described below and in [31]) alongside the model equations. Thus, at the end of one forward model integration, a Gauss-Newton algorithm can than be used to compute the next guess of y_u(0) using the residuals and the gradient matrix as shown below:

$${\mathit{y}}_u^{k+1}(0)={\mathit{y}}_u^k(0)-B_u^{-1}{\mathit{b}}^k.$$ (5)

We note that in general, Gauss-Newton iterations are not guaranteed to converge, but we have found this procedure to work well in practice, because close initial guesses are provided by previous solutions.

B. Efficient Jacobian and Compliance Matrix Computation

For the purposes of inverse kinematic control and intrinsic wrench sensing, we also compute the spatial manipulator Jacobian, J^s, and Compliance matrix, C^s. These matrices can be generalized as continuous functions of arc length, and thus describe the motion of the entire robot with respect to changes in the actuator positions or the components of an applied wrench as,

$${(dg(s)g^{-1}(s))}^{\vee }=J(s,\mathit{q},\mathit{w})d\mathit{q}+C(s,\mathit{q},\mathit{w})d\mathit{w}.$$

where w is the end-effector wrench $\mathit{w}={[\begin{array}{ll}{\mathit{F}}^T& {\mathit{L}}^T\end{array}]}^T$, and the operator ˅: so(3) → ℝ³ is defined in [33] (note that as in [33] we also overload this notation to map se(3) → ℝ⁶).

Our approach for computing J^s(s) and C^s(s) is to numerically integrate their arc-length derivatives which we obtain analytically by differentiating the model differential equation with respect to q and w respectively. To do this, we define vectors $\mathit{y}={[{\theta }_2,\dots ,{\theta }_n,u_{1z},\dots ,u_{nz},{\mathit{m}}_{xy}^{1T}]}^T$, and $\mathit{x}={[{\mathit{q}}^T,{\mathit{w}}^T,{\mathit{y}}_u^t(0)]}^T$. We then define matrices V(s) and E(s) and B as,

$$\begin{array}{l}E=[{\left(\frac{\partial g}{\partial x_1}{g}^{-1}\right)}^{\vee }\dots {\left(\frac{\partial g}{\partial x_{3n+8}}{g}^{-1}\right)}^{\vee }],\\ V=\frac{\partial \mathit{y}}{\partial \mathit{x}},\text{and}B=\frac{\partial \mathit{b}}{\partial \mathit{x}},\end{array}$$ (6)

where for a particular vector x, solution of the associated initial value problem provides g, y, and b.

Commuting derivatives allows us to write $\frac{d}{ds}\left(\frac{\partial \mathit{y}(s)}{\partial \mathit{x}}\right)=\frac{\partial \dot{\mathit{y}}}{\partial \mathit{x}}$. Thus, arc-length derivatives for V and E can be derived by differentiating the model differential equations with respect to x, and these new equations can be integrated simultaneously with the model to efficiently compute E, V, and B. Then, as described in [31], the spatial robot Jacobian and Compliance matrix can be calculated as follows

$$J^s(s)=E_q(s)-E_u(s)B_u^{-1}{B}_q$$ (7)

$$C^s(s)=E_w(s)-E_u(s)B_u^{-1}{B}_w.$$ (8)

where subscripts q, w, and u denote the ∂q, ∂w, and ∂y_u(0) columns of a matrix, respectively.

C. Computational Speed

In a series of numerical experiments, we compared the above method for computing the Jacobian and Compliance matrices via direct integration of their analytical derivatives to the standard brute-force finite differences approach, using Matlab to perform all computations. The results showed that the direct method improved computation speed by a factor 20 over the finite differencing method [31]. We have implemented this model in C++ and integrated it into our teleoperation control architecture and hardware setup described in Sections III-C and IV-D. On an Intel Xeon 2.5 GHz quad core system the model currently computes the converged solution to the model boundary value problem (including external loads), as well as the manipulator Jacobian and Compliance matrices, at a rate of approximately 200 to 400 Hz depending on the robot length (we use a fixed integration step-size of 2 mm), and the number of Gauss-Newton iterations required for convergence (typically 1, occasionally 2 or 3).

D. Teleoperation

In our implementation we adapted the generalized damped least squares approach to the differential inverse kinematics problem as proposed by Wampler in [35]. The basic idea is to convert the problem to finding a set of actuator velocities which minimize a custom-built objective function which takes into account several competing goals: accurately tracking the desired trajectory, maintaining stability, limiting actuator velocities, and avoiding actuator limits and other undesirable configurations. The form of our objective function is,

$$F=\frac{1}{2}({(\mathit{J}\dot{\mathit{q}}-{\upsilon }_0)}^{\mathrm{T}}{\mathit{W}}_0(\mathit{J}\dot{\mathit{q}}-{\upsilon }_0)+\sum _{i=1}^m{(\dot{\mathit{q}}-{\upsilon }_i)}^{\mathrm{T}}{\mathit{W}}_i(\dot{\mathit{q}}-{\upsilon }_i)),$$ (9)

where q̇ is the vector of the actuator velocities, W_i is a non-negative symmetric weighting matrix, υ₀ is the desired end-effector velocity vector, and υ_i is a secondary desired actuator velocity vector, which may be set to zero in order to achieve damping, or set to the gradient of a penalty function which penalizes closeness to undesirable configurations or actuator limits. For example, to keep actuators at tube bases far from collisions, the penalty function could be the sum of squared distances between tube bases, and the gradient would be taken with respect to actuator variables. Setting $\frac{\partial F}{\partial \dot{\mathit{q}}}=0$, we find the necessary condition for q̇ to minimize F:

$$\dot{\mathit{q}}={({\mathit{J}}^T{\mathit{W}}_0\mathit{J}+\sum _{i=1}^m{\mathit{W}}_i)}^{-1}({\mathit{J}}^T{\mathit{W}}_0{\upsilon }_0+\sum _{i=1}^m{\mathit{W}}_i{\upsilon }_i).$$ (10)

For our prototype robot, we used m = 1, with υ₁ = 0 to achieve damping, and W₀ and W₁ were diagonal ma­trices whose elements were tuned manually to achieve a qualitatively good tradeoff between tracking and damping. Specifically we used W₀ = diag{10⁶,10⁶,10⁶,82,82, 820} and W₁ = diag{19,19,19,10⁶,10⁶,10⁶}, and expressed all linear variables in units of meters and all rotational variables in units of radians. Increasing the magnitudes of the elements in W₀ relative to those in W₁ leads to faster convergence to the desired pose, while reducing them will lead to smoother motions. In both W₀ and W₁, the first three values listed relate to positions and the latter three to angles, and relative scaling within each group is indicated by the numerical value listed. Note that as with all damped least squares algorithms, some damping is required for numerical stability.

In our discrete implementation, q̇ represents the finite actuator displacements to be commanded in the next time step, and υ₀ represents the desired end-effector displacements. We compute υ₀ as the difference between the commanded end-effector frame g_c and the most recent model-predicted frame g_p by using the first-order approximation of the constant twist solution ${\upsilon }_0={({\mathit{g}}_p^{-1}{\mathit{g}}_c-I)}^{\vee }$.

We obtain the commanded frame g_c from the master input device by first defining a start time t₀, i.e. when the operator “clutches in” by pressing a button on the input stylus. During the movement of the input device stylus, we apply its relative motion to the predicted frame at t₀, such that

$${\mathit{g}}_c={\mathit{g}}_p(t_0){\mathit{g}}_m^{-1}(t_0){\mathit{g}}_m$$ (11)

where g_m is the master device frame. We note that this formulation gives v₀ in coordinates of g_p such that the body-frame Jacobian should be used in 10. The body Jacobian can be computed from the spatial Jacobian by using the standard adjoint transformation described in [33].

To allow the operator to make more precise movements, motion scaling is achieved by altering the commanded relative motion ${\mathit{g}}_m^{-1}(t_0){\mathit{g}}_m$, which appears in (11). The relative position command is simply scaled by a multiplicative factor less than one, and the rotation matrix is scaled by first transforming to axis-angle representation, scaling the angle by the same multiplicative factor, and then transforming back to the rotation matrix representation. The singularity at the identity in the map from rotation matrices to the axis-angle representation is handled by not performing the scaling for very small relative angles.

E. Image-Guidance

To provide image-guidance in a manner analogous to what skull base surgeons typically use (e.g. BrainLab AG, Medtronic Inc.), we integrated image-guidance with our robot system using magnetic tracking and open-source 3D SLICER software [36]. This enables visualization of the robot's tool tip position with respect to pre-operative medical images. Our display shows the typical triplanar medical image view, with a fourth image showing the 3D surface model of the patient (see Fig. 9). Image-guidance interfaces of this type have been shown to reduce surgical duration and complication rates [37].

Fig. 9.

Experimental setup for the anatomical reachability study. The surgeon teleoperated one active cannula within the ex vivo human skull.

Magnetic tracking is enabled by use of an Aurora system from Northern Digital Inc. We place 5 degree of freedom (DoF) 0.8 mm diameter tracking coils near the tip of the inner tube of the cannula. These provide 1.4 mm RMS position and 0.35° RMS orientation 95% confidence intervals, at 30 Hz, as specified by the manufacturer. We infer the 6th degree of freedom not provided by the magnetic tracker (roll about the tool tip axis) from the angular position of the innermost cannula tube (the tracking coil is attached to the inside of this tube, and moves with it). The tracking information is sent to 3D SLICER over Ethernet using the OpenIGTLinkIF module.

Achieving image guidance requires first registering the robot coordinate frame to the world (i.e. magnetic tracker) coordinate frame. We accomplished this using point-based registration [38], generating the two corresponding point sets required by actuating the robot to 81 distinct poses spanning its configuration space and recording magnetic tracker readings at each. Also, as has been observed in prior work [26], [39], a calibration procedure is useful to optimize imprecisely known model parameters. A parameter vector is created by combining robot-world frame parameters and model parameters, which here consist of the nine quantities $(L_i^s,L_i^c,{\kappa }_i)$ with i ∈ {1,…, 3}. We then use the Nelder-Mead simplex algorithm as implemented in Matlab's fminsearch function to optimize all parameters while minimizing the Euclidean tip error between the two point sets. After registration and calibration, RMS error between the 81 magnetic tracker points and the 81 robot forward kinematics points was less than 1.5 mm.

The last step in achieving image guidance is registering medical images to the world (i.e. magnetic tracker) frame. This was performed using the standard clinical practice of surface-based registration. A tracked digitizing probe (Aurora 6 DoF Probe, Northern Digital Inc., Ontario, Canada) was traced over the surface of the physical cadaver skull, providing surface points in magnetic tracker space. Image data was registered to this point set using an iterative closest point (ICP) algorithm [40], after segmentation of the medical images using thresholding and Delaunay triangulation functions included in 3D SLICER.

V. Experimental Demonstration

For the experimental evaluation of our prototype system, we conducted three experiments: (1) a pick and place demonstration task to determine whether users can manipulate objects with the system, (2) an anatomical reachability task to evaluate the potential of the robot to reach anatomical landmarks of interest in pituitary surgery, and (3) an artificial tumor removal to evaluate surgeons' ability to perform a clinically relevant task. The robot component tubes were as described in Table II. Note that these experiments were conducted before the tube curvature optimization results described in Section III-B were available, which explains the differences in tube parameters reported there and those in Table II. Fortunately this is not problematic, since experimental use of suboptimally shaped tubes is conservative, making our experiments more challenging than they would be with optimally shaped tubes.

Table II. Component Tube Parameters for Experimental Evaluation. All Values in mm, κ in (mm⁻¹).

Cannula	Gripper			Curette
Tube	Outer	middle	inner	outer	middle	inner
$L_i^s$	82.4	241.1	417.6	94.6	241.4	435.6
$L_i^c$	68.6	69.9	38.4	53.4	54.6	39.4
κ	0.0032	0.0059	0.0128	0.0035	0.0068	0.0174
OD	2.32	1.68	1.16	2.32	1.68	1.17
ID	1.87	1.35	0.76	1.87	1.35	0.76

A. Experiment 1: Pick and Place Task

The aim of this demonstration experiment was to determine whether users operating the prototype system are able to reliably pick objects up from one location and place them at another location using a gripper end-effector. The experimental setup was as shown in Fig. 8. A peg board (100×64 mm) was rigidly attached in front of the robot. The pegs were arranged in a hexagon pattern on the left side of the board (horizontal distance 35 mm and vertical distance 17.3 mm between pegs) and in a rectangular pattern on the right side of the board (horizontal distance 30 mm and vertical distance 17.3 mm between pegs). The peg board is part of the Fundamentals of Laparoscopic Surgery Skill assessment and training program [41]. Six plastic rings (radius 4.45 mm) were lined up on the pegs on the right side of the board (see Fig. 8 inset).

Fig. 8.

Experimental setup for the pick and place task. The user was asked to pick up a total of six plastic rings on a peg board (see inset) and place them on the free pegs on the left side of the board.

Users were given some time before the experiment to adjust to the robot and set their preferred motion scaling ratio between input device velocities and robot tip velocities, but no formal training procedure was performed. The user was then asked to transfer all plastic rings from the right side of the board to the free pegs on the left side in any order they preferred. Performance metrics measured were the number of rings successfully transferred, the number of rings dropped, and the task completion time. A total of 10 subjects participated in the experiment, a group that included some expert users with experience using this robot, novices who were new to it, and two surgeons who had a moderate amount of experience with the system.

Results of the experiment are shown in Table III. The mean task completion time was 232.4 s with a standard deviation of 33.7 s over all trials. Only one novice user dropped any rings with that single user dropping two. All other subjects successfully transferred all rings with no drops. The experienced surgeons both recorded times lower than the mean completion time. They also verbally expressed that they were satisfied with their ability to control the end effector in light of the requirements of endonasal pituitary surgery. Interestingly, the novice user group actually performed slightly better than the experienced user group in average task completion time (235 s and 245 s, respectively), though this difference is not statistically significant. The fact that experts were not significantly faster suggests that the learning curve for use of the overall system may not be steep.

Table III. Results for Transfer Task User Study.

	User	Time (s)	Drops
Novice	1	187	0
	2	275	2
	3	237	0
	4	241	0
Expert	5	261	0
	6	206	0
	7	270	0
	8	244	0
Surgeon	9	220	0
	10	183	0

B. Experiment 2: Anatomical Reachability

A second set of demonstration experiments was performed to evaluate the potential of users to use the robot to reach anatomical landmarks of interest in skull base surgery, while at the same time experimentally quantifying the robot's workspace within the anatomical constraints of the nasal cavity. This experiment was performed by an experienced skull base surgeon familiar with the system. The experimental setup was as shown in Fig. 9. The nasal cavity of a natural bone human skull (Skulls Unlimited International, Inc., USA) was prepared by the surgeon, exposing the sphenoid sinus, followed by a CT scan (isotropic voxels of 0.4 mm). A 3D surface model of the skull was generated as described previously using 3D Slicer. The skull was placed on a foam cushion which itself was rigidly attached to the benchtop, such that only slight movements of the skull were possible during the actual experiment. The alignment of robot and skull were chosen such that they reflect the intended clinical setup we foresee. A rigid endoscope (30 degree, 2.7 mm diameter, Olympus) was used for visualization and held in place by a clamp, with its images presented to the surgeon using a standard endoscope cart. The image-guidance view described in Section IV-E was presented on an additional monitor beside the endoscope view. Robot tip positions (from magnetic tracking data) were illustrated with a cross on the image-guidance screen's triplanar CT images.

In the first part of this study the surgeon was requested to move the robot tip to five prominent anatomical landmarks: the rostrum, the superior and mid-point of the roof of the inter-sinus septum, and the left and right sphenoid floor. When the surgeon reached the landmark the current endoscope view and the robot's tip location were recorded. After all locations had been reached, the surgeon was then instructed to move the robot within the nasal cavity, accessing as much of it as possible while robot tip positions were recorded in real time using the magnetic tracker. Fig. 10b shows five superimposed endoscopic views of the robot successfully reaching the five desired anatomical locations. Fig. 10c shows the workspace accessed by the surgeon during subsequent teleoperation. The figure illustrates that the entire workspace is accessible to the surgeon through the robot, with no visible workspace gaps.

Fig. 10.

Results of anatomical reachability study. (a) Photograph of the robot tip touching the inter-sinus septum. (b) Five superimposed endoscope images showing the robot tip at five anatomical landmarks in the sphenoid sinus. (c) Recorded robot tip positions visualized with the 3D surface model of the skull (laterally clipped, anterior view in inlay image). The surgeon was asked to move the robot to all locations possible.

C. Experiment 3: Artificial Tumor Removal

The aim of this experiment was to determine whether surgeons could teleoperate the robot to remove a tumor with the curette end-effector. Two experienced skull base surgeons used the robot to resect as much of an artificial pituitary tumor in a phantom skull as possible. First, an anatomical skull model (#A20, 3B Scientific, Germany) was prepared by a surgeon to closely replicate conditions at the start of pituitary tumor resection. Then artificial tumor tissue judged to be qualitatively similar to pituitary tumor tissue by experienced surgeons was created using a 5:1 ratio of water to ballistic test media (SIM-TEST, Corbin Inc., White City, USA). This tissue was formed into the shape of a pituitary tumor and inserted into the sella turcica of the skull. The skull and endoscope were held in place during the experiment, while suction was used periodically to clean the curette. Note that the suction was not at any time used to directly remove the simulated tumor itself; only the robot was used for resection. The evaluation metric measured was the percentage of tumor tissue removed, determined by weighing the skull before insertion of the artificial tumor and after the user finished the resection.

Two simulated tumor removal experiments were conducted. In both cases, all tumor was removed other than a thin film of material on the bone surface and in crevices at the back of the sella. In the first experiment, one surgeon performed the procedure alone from start to finish, with 308 mg of an initial tumor mass of 1400 mg remaining after the procedure (78% resection). In the second, two surgeons collaborated on the resection, taking turns operating the robot with 693 mg of an initial tumor mass of 2100 mg remaining after the procedure (67% resection). While no time limit was suggested or imposed, both were completed in a time period comparable to that of a clinical endonasal pituitary tumor removal.

In assessing these results, it is important to note that no current method exists for measuring residual tumor volume after surgery in live humans. However, it is known that surgeons are rarely (if ever) able to resect 100 % of the tumor using current surgical techniques, yet outcomes remain good for those patients fortunate enough to undergo endonasal surgery rather than traditional procedures. Indeed, one clinical study revealed “definite tumor remnants or at least suspicious findings” in 42 % of patients in postoperative MRI scans [42]. However, the inability to conclusively differentiate tumor boundaries with respect to surrounding healthy tissues precludes image-based volume measurements. But because pituitary tumors are usually benign and slow growing, the goal of the surgery is decompression. This would have been achieved given the resection percentages demonstrated in our experiments.

VI. Discussion & Conclusion

In this paper, we described the design, control, integration of image-guidance, and evaluation of a robotic system for transnasal skull base surgery. This design process illustrates how the mature models for concentric tube robots that have been developed in the past few years can be used to enable model-based design and control of concentric tube robots to meet the needs of a specific surgical procedure. Our experiments indicate that users of widely varying skill levels and backgrounds can successfully use the robot to accomplish laparoscopic training tasks. They also illustrate that experienced surgeons can use the robot to target sites of clinical interest at the skull base, access their desired workspace, and successfully resect simulated pituitary tumors.

Opportunities for future enhancement to the system include the addition of a wrist at the tip of the cannula, which would make dexterous surgical maneuvers deep in the sella easier to accomplish. Our experiments have also led us to believe that haptic feedback may be more useful in skull base surgery than we would have anticipated. Surgeons using our robot indicated that they are used to feeling the contact of their instruments with bone, to identify the extents of the cavity in which they are working. While surgeons felt that they were able to adapt to use of pure vision (i.e. visually observing the deflection of the robot) to identify bone contact, they also felt that haptic feedback would be desirable. Fortunately, continuum robots are capable of deflection-based or “intrinsic” force sensing [43], [44]. Thus, in the future we plan to apply the general continuum robot probabilistic deflection-based force sensing framework of [44], together with our kinematic model that accounts for external loads to estimate the forces applied to the concentric tube robot, with the goal of providing haptic feedback to the surgeon.

Other opportunities for future research include investigation of alternate kinematic mappings for teleoperation and alternate user interfaces. While the Phantom Omni interfaces are a useful first step, it remains unclear how a human can most intuitively and completely specify the shape of a continuum robot, and how much of the robot shape should be left to automatic motion planning algorithms. Motion planning and tube design algorithms are also open areas of research. Advanced tube design algorithms that do not make the restrictive initial choices we made in this work to simplify the design problem would be useful. It will also be important in the future to include energy bifurcations (see [39]) into the design process to either design bifurcation free robots or to avoid bifurcations through control. Accomplishing this will require the development of general methods to predict bifurcations.

Lastly, we believe the work described in this paper, together with other recent results adapting concentric tube robots to cardiac surgery [45], foreshadow a bright future for concentric tube continuum robots. Many clinically useful applications for these robots were foreseen soon after they were invented (see [46] for an overview). But it is only recently, catalyzed by the maturation of mechanics-based models, that the potential of concentric tube robots is beginning to be unlocked in practice.

Biographies

Jessica Burgner received the Diplom (Dipl.-Inform.) in computer science from the University of Karlsruhe (TH), Germany, in 2006 and the Doctorate degree (Dr.-Ing.) in computer science from the Karlsruhe Institute of Technology, Germany, in 2010.

From Sep. 2010 to Oct. 2012 she was postdoctoral research associate in the Medical & Electromechanical Design Laboratory of the mechanical engineering department at Vanderbilt University, Nashville TN. In 2012, she joined the Hannover Centre for Mechatronics at Leibniz Universtaet Hannover in Germany. Her current research interests include surgical robotics and image–guided interventions. She received the Emmy-Noether Young Researcher's Excellence Career Award from the German Research Foundation in 2013.

D. Caleb Rucker (S'07) received the B.S. degree in engineering mechanics and mathematics from Lip-scomb University, Nashville, TN, in 2006. In 2007, he was an Engineer with Jacobs Technology Group, Tullahoma, TN. He received the Ph.D. degree in mechanical engineering from Vanderbilt University, Nashville TN.

His current research interests include medical robotics, continuum robotics, soft-tissue mechanics, control, and sensing.

Hunter B. Gilbert received the B.S. degree in mechanical engineering from Rice University in Houston, TX in 2010. Since then he is a pursuing his Ph.D. in mechanical engineering at Vanderbilt University in Nashville, TN, in the Medical and Electromechanical Design Laboratory. He is currently researching medical robotics and continuum robotics. He received the NSF Graduate Research Fellowship in 2012.

Philip J. Swaney received the B.S. degree in mechanical engineering from The Pennsylvania State University, State College, PA in 2010. He is pursuing his Ph.D. degree in mechanical engineering at Vanderbilt University, Nashville TN. His current research interests include medical robotics, continuum robots, and interface design and control. He received the NSF Graduate Research Fellowship in 2012.

Paul T. Russell III received his MD from Texas Tech University Health Sciences Center School of Medicine, completed his residency at Baylor College of Medicine, and Rhinology Fellowship at Vander-bilt. His patient care emphasis is in rhinology and sinus diseases; he also performs endoscopic anterior skull base surgery and teaches medical students & residents. He is on the VUMC Clinical Development Committee.

Kyle D. Weaver received his B.S. from Duke University in 1988. He then proceeded to obtain his M.D. and completed his neurosurgical training in 2002, both at the University of North Carolina-Chapel Hill. This was followed by completion of a brain tumor fellowship at Johns Hopkins University in Baltimore, M.D. He joined the faculty of the Vanderbilt University Department of Neurological Surgery in 2004 where he is currently Co-Director of the Vanderbilt Pituitary Center and also holds a joint appointment in otolaryngology. He is also active in the Vanderbilt Brain Tumor and Skull Base Programs.

Robert J. Webster III (S' 97 - M' 08) received the B.S. degree in electrical engineering from Clemson University, Clemson, SC, in 2002 and the M.S. and Ph.D. degrees in mechanical engineering from the Johns Hopkins University, Baltimore, MD, in 2004 and 2007, respectively.

In 2008, he joined the Faculty of Vanderbilt University, Nashville, TN, as an Assistant Professor of mechanical engineering, where he currently directs the Medical & Electromechanical Design Laboratory. His current research interests include medical robotics, image–guided surgery, and continuum robotics. Prof. Webster received the IEEE Volz award for PhD thesis impact as well as the NSF CAREER Award in 2011.