Box 1.
Vesicle-shape phase diagram
|
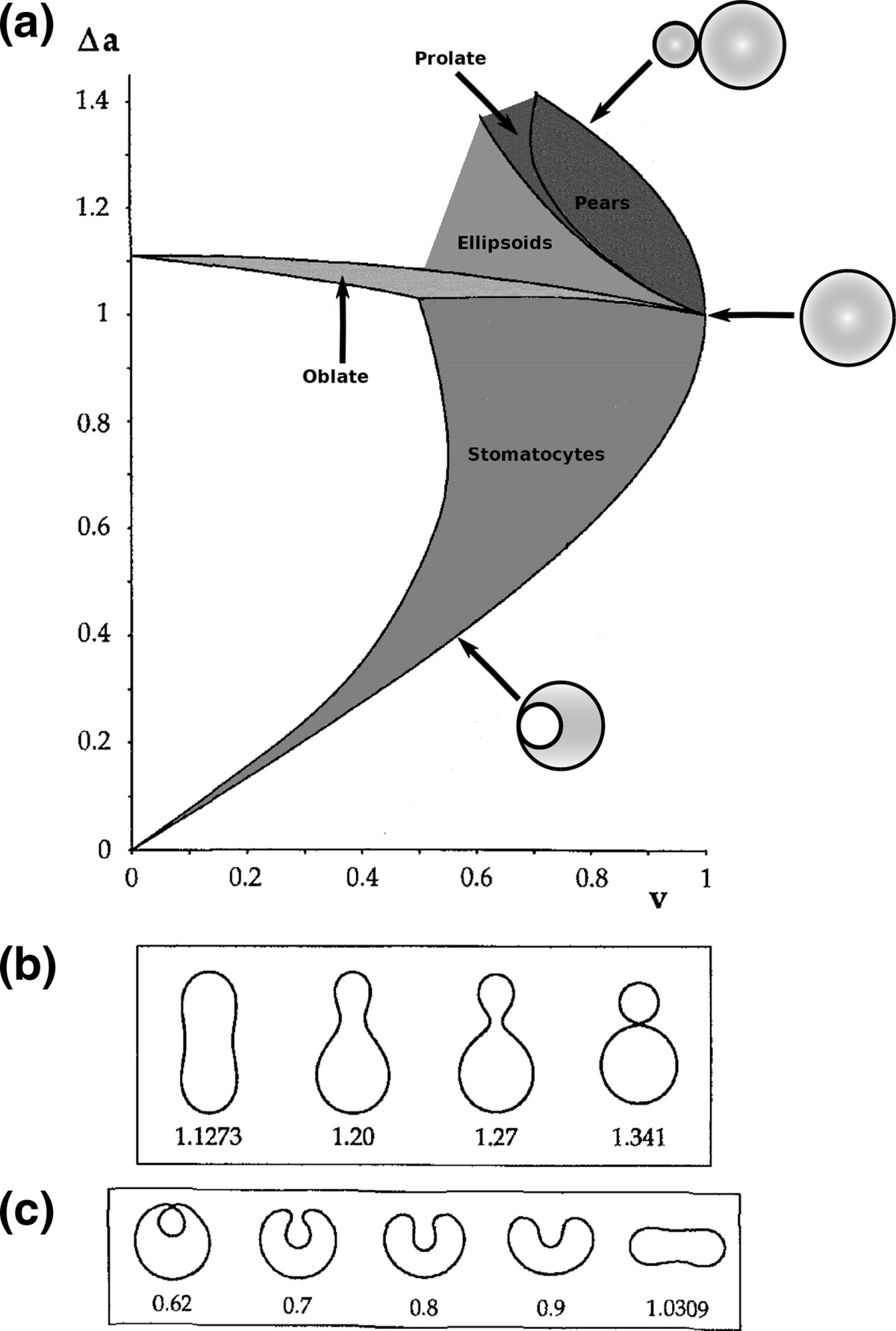
a Phase diagram of the strict-bilayer-coupling model showing different classes of shapes. Areas in white were not explored. Note that a sphere is the point 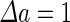 and and 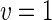 . b Different stable shapes along the shape-trajectory from a prolate to two spheres connected by a narrow neck through the pears class for the line . b Different stable shapes along the shape-trajectory from a prolate to two spheres connected by a narrow neck through the pears class for the line 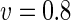 . The value of . The value of 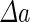 for each shape is stated below it. c Different stable shapes along the shape-trajectory from a prolate to a sphere inside a sphere shape through the stomatocyte class for the line for each shape is stated below it. c Different stable shapes along the shape-trajectory from a prolate to a sphere inside a sphere shape through the stomatocyte class for the line 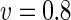 . The value of . The value of 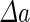 for each shape is stated below it. All panels were modified with permissions from reference Seifert et al. (1991) for each shape is stated below it. All panels were modified with permissions from reference Seifert et al. (1991)  (1991) American Physical Society. Panel a was compiled by the aid of reference Svetina (2009). (1991) American Physical Society. Panel a was compiled by the aid of reference Svetina (2009).Deformation of a 2-D surface embedded in a 3-D space can involve either stretching or bending of the surface. These reversible deformation modes cost elastic energy. Since the exposure of the hydrophobic moieties of the molecules in an amphiphatic membrane to the aqueous environments costs a relatively large amount of energy, the main deformation mode of membranes is bending, that is, changes in the curvature of the membrane. Differential-geometry considerations show that, for a general surface, one can define two principles curvatures, 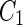 and and 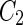 that are associated with the two perpendicular tangents to the surface. Two measures for the curvature of a shape can be constructed from that are associated with the two perpendicular tangents to the surface. Two measures for the curvature of a shape can be constructed from 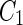 and and 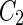 , the mean curvature , the mean curvature 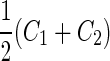 and the Gaussian curvature and the Gaussian curvature 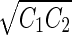 . Form these two measures, one can calculate the bending energy of a piece of surface ( . Form these two measures, one can calculate the bending energy of a piece of surface (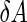 ) as ) as 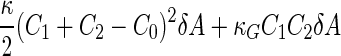 , where , where 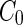 is the local spontaneous curvature and is the local spontaneous curvature and 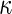 and and 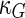 are the mean and Gaussian bending moduli, respectively. The total elastic energy in this case is the integral of these two terms over the whole surface of the vesicle. It was shown, however, that these two terms alone cannot account for the behavior of lipid membranes. The reason is that a lipid bilayer membrane is composed of two leaflets, so that when it bends, one layer is stretched and the other one is compressed. Hence, an additional term is added to the elastic energy that describes the coupling between the two layers. One thus arrives at the so-called, area-difference-elasticity model, where the elastic energy ( are the mean and Gaussian bending moduli, respectively. The total elastic energy in this case is the integral of these two terms over the whole surface of the vesicle. It was shown, however, that these two terms alone cannot account for the behavior of lipid membranes. The reason is that a lipid bilayer membrane is composed of two leaflets, so that when it bends, one layer is stretched and the other one is compressed. Hence, an additional term is added to the elastic energy that describes the coupling between the two layers. One thus arrives at the so-called, area-difference-elasticity model, where the elastic energy (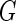 ) equals ) equals |
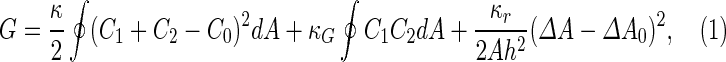
where 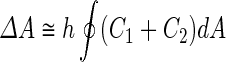 is the area difference between the two leaflets for a given shape, is the area difference between the two leaflets for a given shape, 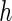 is the width of the membrane, is the width of the membrane, 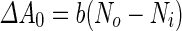 the area difference that is associated with the number of molecules in the outer ( the area difference that is associated with the number of molecules in the outer (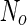 ) and inner ( ) and inner (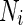 ) leaflets and the preferred area per molecule due to the hydrophobic packing ( ) leaflets and the preferred area per molecule due to the hydrophobic packing (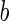 ), and ), and 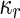 the non-local bending modulus. Since the integral of the Gaussian curvature is topology invariant and changes only when fusion or fission events add or removes holes in a vesicle, it is usually omitted from the calculation. By defining the non-local bending modulus. Since the integral of the Gaussian curvature is topology invariant and changes only when fusion or fission events add or removes holes in a vesicle, it is usually omitted from the calculation. By defining 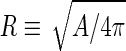 , it is customary to work in reduced dimensionless variables , it is customary to work in reduced dimensionless variables 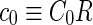 , , 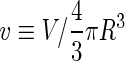 , , 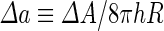 and and 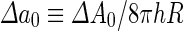 . The ratio . The ratio 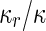 determines the relative contribution of the local and non-local bending terms. For the case determines the relative contribution of the local and non-local bending terms. For the case 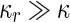 , one can omit the last term of the elastic energy, and impose instead another hard constrain , one can omit the last term of the elastic energy, and impose instead another hard constrain 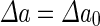 . This limit is called the strict-bilayer-coupling model. The other limit where . This limit is called the strict-bilayer-coupling model. The other limit where 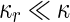 is called the spontaneous-curvature model, and in that case the elastic energy is simply taken to be is called the spontaneous-curvature model, and in that case the elastic energy is simply taken to be 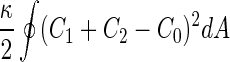 . Interestingly, this limit is identical to the original model that was introduced by Canham Helfrich and Evans for the understanding of the shape of red blood cells and which led to the development of the full area-difference-elasticity model (Canham 1970; Helfrich 1973; Evans 1974). The result of these models is a phase diagram in the . Interestingly, this limit is identical to the original model that was introduced by Canham Helfrich and Evans for the understanding of the shape of red blood cells and which led to the development of the full area-difference-elasticity model (Canham 1970; Helfrich 1973; Evans 1974). The result of these models is a phase diagram in the  (or (or  ) space with a gallery of shapes like spheres, prolates, oblates, pears, cigars and stomatocytes, as can be seen in the figure. For a continuous change in the values of ) space with a gallery of shapes like spheres, prolates, oblates, pears, cigars and stomatocytes, as can be seen in the figure. For a continuous change in the values of  (or (or 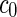 ), the shape of the vesicle changes along a shape-trajectory in the phase diagram ), the shape of the vesicle changes along a shape-trajectory in the phase diagram | |
