Abstract
In Förster resonance energy transfer (FRET) experiments, extracting accurate structural information about macromolecules depends on knowing the positions and orientations of donor and acceptor fluorophores. Several approaches have been employed to reduce uncertainties in quantitative FRET distance measurements. Fluorophore-position distributions can be estimated by surface accessibility (SA) calculations, which compute the region of space explored by the fluorophore within a static macromolecular structure. However, SA models generally do not take fluorophore shape, dye transition-moment orientation, or dye-specific chemical interactions into account. We present a detailed molecular-dynamics (MD) treatment of fluorophore dynamics for an ATTO donor/acceptor dye pair and specifically consider as case studies dye-labeled protein-DNA intermediates in Cre site-specific recombination. We carried out MD simulations in both an aqueous solution and glycerol/water mixtures to assess the effects of experimental solvent systems on dye dynamics. Our results unequivocally show that MD simulations capture solvent effects and dye-dye interactions that can dramatically affect energy transfer efficiency. We also show that results from SA models and MD simulations strongly diverge in cases where donor and acceptor fluorophores are in close proximity. Although atomistic simulations are computationally more expensive than SA models, explicit MD studies are likely to give more realistic results in both homogeneous and mixed solvents. Our study underscores the model-dependent nature of FRET analyses, but also provides a starting point to develop more realistic in silico approaches for obtaining experimental ensemble and single-molecule FRET data.
Introduction
Förster resonance energy transfer (FRET) has become a commonly used approach in structural molecular biology and biophysics to obtain three-dimensional information about the structure of macromolecules in solution (1–7). Theoretically, FRET occurs through the nonradiative transfer of energy between two fluorophores, namely, an electronically excited donor and a ground-state acceptor. The efficiency of energy transfer, E, is strongly distance dependent and is given by
| (1) |
where R is the distance between the fluorophore transition-dipole moments and R0 is the separation at which E is 50%. R0 depends on the spectroscopic characteristics of specific donor-acceptor dye pairs and the spatial relationship between fluorophores (8). In principle, given a theoretical value of R0, Eq. 1 makes FRET a very powerful tool for measuring distances in the range of 1–10 nm (1–6,9–16).
Electronic interactions between the donor and acceptor are normally considered in the weak-coupling limit (17). A number of approximations, including the so-called ideal-dipole approximation (IDA) (18,19), are used to derive a tractable dependence of the energy-transfer rate on the relative orientations of the dye transition-dipole moments (20,21). Nevertheless, independent measurements of the dipole orientation factor, κ2, are rarely available, which leads to widespread replacement of the actual value of this factor with its isotropically averaged value of 2/3 (22–25). The dependence on κ2 is embedded in the value of , given in nm6, by
| (2) |
where ΦD is the quantum yield of the donor fluorophore, J(λ) is the donor-acceptor spectral overlap integral in units of M−1 nm3, NAv is Avogadro’s number, and n is the refractive index of the medium, taken to be that of water at 20°C, 1.333, or 1.4 for water/glycerol mixtures at 20°C. The value of κ2 lies between 0 and 4 and depends on transition-moment dipole orientations through
| (3) |
where θT is the angle between the donor and acceptor transition dipole vectors, , and , respectively, and θD and θA are the respective angles and make with the vector connecting the centers of the donor and acceptor molecules (see Fig. 1). The value κ2 = 2/3 is obtained by spherical averaging over all three of the angles that appear in Eq. 3 (20,22,26,27).
Figure 1.
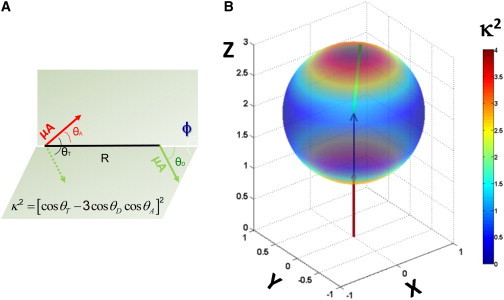
(A) Geometric definition of the dipole-orientation factor, κ2, as a function of the spatial relationship between donor and acceptor transition-dipole moments (green and red arrows, respectively). (B) Three-dimensional heatmap showing the dependence of κ2 on the polar angle between the donor transition moment and the vector between fluorophore centers of mass, . Here, the acceptor transition moment and are coaxial and oriented along the z axis. Under these conditions, κ2 can take on the full range of possible values from 0 to 4. Two extreme cases can clearly be identified in which the donor and acceptor transition moments are parallel (κ2 = 4) or perpendicular (κ2 = 0). (Two columns, 6.50″ W × 4.41″ H.) To see this figure in color, go online.
Despite the technique’s sensitivity and versatility, the analysis of FRET measurements in terms of macromolecular structure remains a challenge. FRET methods typically involve organic fluorophores conjugated to the molecule(s) of interest. These dyes are often bulky and attached by a linker chain of significant length. Although potential restrictions on dye motions are often acknowledged, the assumption of isotropic fluorophore motions is often used nonetheless. This assumption is invalid in many applications (17,28–30), which can prevent FRET from being used as a truly quantitative technique for accurately measuring inter- or intramolecular distances. In addition to the unknown value of κ2, other uncertainties militate against determining accurate distances from E and whether temporal or ensemble averaging of κ2 is appropriate. However, measuring the anisotropy of the donor and acceptor transition-dipole moments sets limits on κ2 and can significantly reduce uncertainties in the calculated distances (20,22,31,32).
Models based on surface accessibility (SA) are widely used to quantify donor-acceptor geometry in FRET (2,33–35). SA models probe the FRET-dye positions with respect to a static molecular structure of interest. These calculations are based on simple geometric sampling algorithms that approximate the dyes by spheres of a given radius, each connected to the macromolecule by isotropically flexible, but possibly inextensible, linkers. A Monte Carlo (MC) search finds all possible dye positions that do not violate the steric and tethering constraints, thereby defining accessible volumes of presumed uniform density occupied by each dye in the system. The SA values of the transfer efficiency, <E>, are subject to many sources of error, including the fact that most dye molecules are not spherical—a steric factor that can contribute to deviations in κ2 from its isotropic value. Although fluorophore emission anisotropy measurements can reduce uncertainties in κ2, interpretation of these data requires assumptions about details of fluorophore motion that are difficult to corroborate experimentally (20,22,31).
Errors in <E> also increase if the molecular environment of the dyes affects either the positional or orientational distribution of the transition dipole moments (23,24,28–30,33,36,37). Although molecular-dynamics (MD) simulations are computationally more expensive, they may be more accurate than SA models of fluorescently labeled macromolecules because they provide more detailed insight into fluorophore behavior at the molecular level and can include details such as fluorophore-macromolecule and fluorophore-solvent interactions. A number of studies have employed MD simulations to examine the behavior of dye pairs used in FRET experiments (23,24,28,38–40). Corry and Jayatilaka (38) used atomistic MD simulations to investigate the mobility of fluorophores conjugated to a protein and its effect on FRET efficiency. In another MD study, Iqbal et al. (39) addressed the effects of dye orientation on FRET data analysis, especially in the case of DNA-conjugated cyanine (Cy) dyes. Recently, Hoefling et al. (41) used a fusion of MC and MD techniques to compute statistical distributions of photon bursts and associated single-molecule FRET-efficiency histograms.
In a recent experimental study (42), we used an SA model to interpret ensemble FRET measurements of target-site synapsis in the Cre recombination system. Although that approach did not depend on interpretation of the FRET signal in terms of absolute distances between donor and acceptor fluorophores, the experimentally measured E value of the synaptic complex was smaller than expected for isotropically averaged fluorophores tethered to crystallographic models of Cre-recombination intermediates. We concluded in that work that the discrepancy could be due to failure of the isotropy assumption, departure of the synaptic-intermediate conformation from the crystallographic structures, or some combination of these factors.
In this work, we compare an SA analysis of donor/acceptor fluorophore distributions with results obtained from more realistic MD simulations for dye pairs in solution and in Cre recombinase-DNA complexes, which serve as a case study. Our main aim here is to investigate the inherent spatial confinement of a donor-acceptor FRET pair in structures of Cre-DNA synaptic complexes using MD simulations. We assess how this confinement and changes in solvent conditions might affect the interpretation of experimental FRET data in this system, particularly with regard to the effects on dye-distance distributions and deviations from isotropic fluorophore motion on submicrosecond timescales. The motions of the donor and acceptor fluorophores (ATTO 594 and ATTO 647N, respectively) used in Shoura et al. (42) are significantly restricted by the dye-accessible volumes within the intermediate complexes. Such restrictions are less severe in free nucleic acid or peptide studies, where the fluorophores are expected to rotate and diffuse to a significant extent, thereby making the isotropically averaged value of κ2 more plausible (23). We emphasize that our simulation timescale is not expected to capture large-scale conformational changes in these large protein-DNA complexes.
Specific enzymatic reaction conditions that include significant concentrations of reagents such as glycerol or polyethylene glycol (PEG) may perturb the interactions of the fluorophores with their immediate environment. In this work, we examined the effect of glycerol on dye-distance distributions and κ2, and hence on distance measurements derived from experimental values of E. It is challenging to maintain adequate conformational sampling in glycerol/water mixtures because of the longer timescale of molecular motion compared with aqueous simulations. Therefore, we used extended trajectories for glycerol/water MD simulations that had up to four times the duration of the corresponding aqueous trajectory (see Table S1 in the Supporting Material). We found that significant concentrations of glycerol substantially altered the balance of dye-dye and dye-macromolecule interactions, leading to dramatic differences between MD and SA dye-distance distributions that were largely uncorrelated with <κ2>. Therefore, our results should prompt a more systematic examination of solvent effects on the behavior of conjugated fluorescent probes. This will provide insights that pertain to FRET-data analysis of large systems beyond examples of labeled macromolecules in mixed solvents (43) such as fluorescent micelles and lipids (44).
Materials and Methods
System specifications
Four different systems were simulated by MD in the course of this work: 1), donor and acceptor fluorophores tethered to fixed points in space by six-carbon linkers; 2), a DNA duplex bearing the loxP sequence in its standard B-DNA form modeling the product of the Cre-recombination reaction in Shoura et al. (42), where donor and acceptor fluorophores are conjugated to C5 positions of adjacent thymine residues on opposing strands; 3), the Cre Holliday-junction intermediate (HJ) complex based on the PDB cocrystal structure 3CRX (45) with fluorophore labels at sites corresponding to the positions used in Shoura et al. (42); and 4), a fluorophore-labeled Cre-mediated synapse of DNA duplexes based on the PDB cocrystal structure 5CRX (46). In keeping with our effort to replicate the experimental system used in Shoura et al. (42) as closely as possible, we used ATTO 647N as the acceptor fluorophore. The structure of ATTO 594, which was used experimentally as the donor fluorophore, remains proprietary. Therefore, we modeled the donor fluorophore using the known structure of ATTO 610, which shares a common conjugated ring system with the 12 published ATTO-dye structures. The isotropic value of R0, R0,iso, for the ATTO 610/647N donor-acceptor pair is 7.3 nm, which is closely comparable to that for the ATTO 594/647N pair (7.5 nm). Finally, we replaced the noncanonical DNA sequence in the lox recombination-site spacer of 3CRX to regenerate the wild-type loxP target site.
MD simulation protocol
Simulations were carried out using the NAMD software package (47) with force-field parameters based on the CHARMM libraries (48). CHARMM 27 parameters were used for nucleic acid and protein moieties, whereas new topology files were created for the fluorophores (ATTO 610/647N) as well as the six-carbon linker chain that connects the fluorophores to the C5 positions of specific thymine residues (see Fig. 2).
Figure 2.
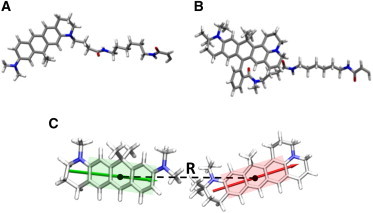
Molecular structures of the fluorophores used in this work. (A) Canonical structure of the donor, ATTO 610, conjugated to a C-6 linker. (B) Structure of the acceptor dye, ATTO 647N, attached to the same linker shown in (A). (C) Geometry-optimized structures of fluorophore ring systems corresponding to the donor excited state and acceptor ground state obtained from ab initio quantum-mechanical calculations. The directions of the transition-dipole moments are indicated (arrows). We define R as the distance between the centers of mass of rigid three-ring conjugated systems corresponding to each dye. (One column; 3.25″ W × 2.34″ H.) To see this figure in color, go online.
Simulation details
In vacuo simulations were run using Langevin dynamics at 300 K under isochoric conditions. Simulations of solvated systems used the TIP3P water model and a constant pressure of 1 atm was maintained using a Nose-Hoover-Langevin piston (49). A time step of 2 fs was used in all simulations in conjunction with the RATTLE/SHAKE algorithm to constrain the bonds between hydrogen and heavy atoms at their equilibrium distances during the dynamics. A nonbonded cutoff of 1.2 nm with a smooth switching function between 1.0 nm and 1.2 nm was used for van der Waals interactions and the short-ranged component of the electrostatic interactions, whereas long-ranged electrostatic interactions were treated using the particle-mesh Ewald method. Pair-neighbor lists were maintained for particles within 1.35 nm of one another.
Simulation procedure and data analysis
Simulations containing protein and/or DNA were performed in three stages. In the first stage, short (∼1 ns) simulations were run in which the atomic positions of the polypeptide and/or nucleic acid backbones were constrained to their initial positions using a soft harmonic constraint of the form
| (4) |
where kH is a harmonic force constant, is the position of a constrained atom, and is the initial (reference) position. The value of kH was set at 5 kcal mol−1 Å−2. In the second stage, the system was allowed to relax with constraints applied only to the terminal basepairs of the DNA structures; this prevents the terminal residues from acting as free ends, which is not the case in experiments. In the third stage, longer simulation times were used. Data were collected only from the third stage of each simulation, where constraints were maintained on the terminal basepairs of the DNA and the systems were taken to be at thermodynamic equilibrium. The minimum trajectory duration exceeded 35 ns for all simulation results reported here.
To monitor the convergence of trajectories for all systems simulated in this study (see Table S1), we used several methods, including block averaging and autocorrelation analysis. Block-averaging analysis consists of reblocking the apparent standard error (SE), σ, of the time average of κ2, <κ2(t)>T, as a function of time over the duration of a given trajectory (50). Here, <f(t)>T denotes , where T is the duration of a trajectory. Block-size-dependent values, σj, are computed sequentially using block sizes of j = 3, 4, 5,…, N frames with N the total number of frames in a trajectory. An estimate of the SE in <κ2(t)>T for the complete trajectory, σ∗, is obtained by fitting σj as a function of j to an exponential growth curve as shown in Fig. S1. This method, though straightforward, leads to a lower bound for σ∗ and is limited by the size of the data set. The dependence of σj on j is not expected to approach a finite value σ∗ if the parameter distribution is not equilibrated. Although we could have run multiple simulations of the same DNA-Cre system using different initial positions for the dyes as a test for convergence, in principle, the ATTO dyes are bulky substituents and are not arbitrarily accommodated within the structure of the protein-DNA complex. As a result, we could not generate two significantly different initial configurations of dyes within the core of the Cre-HJ complex without seriously violating steric and geometric constraints.
We used the dye positions and orientations to compute the time-dependent anisotropy (40), , where is the transition dipole moment at time t and P2 is the second Legendre polynomial, as well as the autocorrelation function for κ2, C(κ2,κ2;τ) = <κ2(t)κ2(t + τ)>T (Figs. S2 and S3). We compared time-averaged dynamic quantities computed from the trajectories, <f(t)>T, with ensemble averages of the same quantities taken over all configurations of the system, <f>. In the limit of an ergodic system in which both the time T and number of systems in the ensemble are arbitrarily large (a condition that is virtually never met in computer simulations), <f(t)>T and <f> are identically equal (51). In the ergodic limit, this equivalence extends to the corresponding experimental quantity, which we specify in our notation by dropping the angle brackets (e.g., the theoretical FRET efficiency <E(t)>T ≃ <E> asymptotically approaches the experimental value, E).
Structure and parameterization of the fluorophores
We assigned the atomic partial charges on the ATTO dyes using the CHARMM convention for all atoms other than nitrogen and atoms belonging to the fluorophore structures. We determined the charges for these atoms by scaling the fitted electrostatic potential (ESP) charges from ab initio quantum-mechanical calculations described below, making sure to conserve the total charge. The equilibrium values of bond lengths and angles were either taken directly from the CHARMM force field for known interactions or iteratively adjusted to match values from ab initio geometry-optimized structures (see below). Force constants for bond stretching and bond-angle displacement were largely assigned by analogy with existing parameters in the CHARMM 27 force field. When suitable parameters were not available from the CHARMM force field, the fully compatible CGenFF force-field parameters were used instead. Parameters for the bond torsions and nonbonded interactions were found in a similar manner.
We note that force-field parameterization may play a considerable role in the observed behavior of the dyes. It is presently unknown what level of theory is necessary to accurately model dye behavior; for example, approaches under development involving polarizable force-field terms (52) or mixed quantum-/molecular-mechanics approaches (53) may give more realistic behavior. Also, interaction parameters that are generated automatically using standard software packages are not always accurate; for example, such parameters do not always capture the aromaticity of conjugated atoms. For the calculations in this work, we checked the final dye parameters against those that were automatically generated through the ParamChem interface and found them to be in good agreement. Detailed force-field parameters for the ATTO dyes are given in topology-file format as an Appendix in the Supporting Material.
Ab initio quantum-mechanical calculations
Hartree-Fock quantum calculations were carried out on the conjugated portions of the donor and acceptor fluorophores that comprised the planar ring system of each dye (38). An initial conformational search was implemented using the OPLS molecular-mechanics force field prior to geometry optimization using a 6-31G∗∗ basis set. Single-point calculations were carried out from these structures using a 6-31+G∗∗ basis set and were used to fit the ESP charges to atomic nuclei. In addition, CIS evaluations were implemented to find the transition-dipole moments of the dyes (see Fig. 2). All ab initio calculations were carried out using the Jaguar software package by Schrödinger (Portland, OR).
Stability of simulated systems
We monitored the van der Waals and electrostatic components of protein-protein and protein-DNA interaction energies in the modified 3CRX structure modeled in these simulations. These calculations were done with and without conjugated dyes. The interaction-energy values serve two main functions: 1), to provide one of several internal checks on the validity of the simulation; and 2), to ensure that the conjugated dyes do not strongly destabilize the 3CRX complex. The results show that there are negligible differences in the total protein-protein and protein-DNA interaction energies for dye-labeled and unlabeled complexes (Fig. S4).
Simulations in glycerol/water mixed-solvent systems
Because of the complexity of simulating a Cre-DNA complex suspended in the actual components of the buffer used in Shoura et al. (42), we chose to approximate the experimental buffer system by using a glycerol/water mixture with a bulk dielectric-constant value similar to that of the experimental buffer. We generated a single, large solvent box containing only the glycerol/water mixture by combining two smaller homogeneous boxes of each component and allowing the solvents to equilibrate (54). Two previously equilibrated simulation cells with dimensions 7.5 × 7.5 × 7.5 nm3, each containing 0.2 M NaCl in either water or glycerol, were merged to obtain a large solvent box of size 15 × 7.5 × 7.5 nm3. The mole fraction of glycerol was 0.39 (2796 glycerol and 4428 water molecules), which approximates that of the nonaqueous components in some experimental Cre-recombination buffers (42,55). We verified that the concentrations of the two solvents were spatially uniform before introducing the solutes. Solvation was performed by superimposing the solute and mixed-solvent simulation boxes; solvent molecules having atoms within 0.15 nm of solute atoms were discarded.
Results and Discussion
Dynamics of tethered ATTO dye pairs
We carried out a series of simulations on solvated donor/acceptor dye pairs in which each dye molecule was tethered by its linker to a fixed point in space (Fig. 3). The tethering points were separated by a distance d along the long central axis of the simulation cell, and the through-space distance between dye centers of mass, R, and the orientation factor, κ2, were monitored for these trajectories. These simulations had the following objectives: 1), to confirm that <κ2> approaches its isotropic value of 2/3 for dyes without restricted rotation; 2), to estimate the minimum length of a trajectory needed to equilibrate the system with respect to sampling of dye orientations; and 3), to investigate the dependence of κ2 on R in aqueous and glycerol/water solvent systems.
Figure 3.
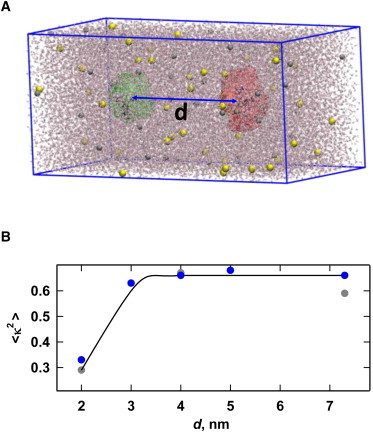
(A) Typical simulation of tethered linker-conjugated fluorophores. A snapshot of a particular configuration of water molecules and ions (0.2 M NaCl; Na+ in gray, Cl− in yellow) is superimposed on the donor (green) and acceptor (red) positions integrated over the course of a 40-ns trajectory. Values of the tethering distance, d, were varied from 2 nm to 7.3 nm (shown). (B) Dependence of <κ2(t)>T on d for MD simulations in aqueous and glycerol/water solvent systems; the continuous curve is merely a guide for the eye. Note that <κ2(t)>T assumes the isotropic value of 2/3 for all but the smallest value of d (2.0 nm). (One column, 3.25″ W × 3.10″ H.) To see this figure in color, go online.
Over the range of d = 3.0–7.3 nm, <κ2(t)>T was found to be 0.66 ± 0.04, which is essentially identical to the isotropically averaged value of 2/3 in both aqueous and glycerol/water simulations. However, this was not the case for d = 2.0 nm, where <κ2 (t)>T = 0.33 for aqueous simulations and 0.29 for glycerol/water. This pronounced decrease in <κ2(t)>T in both solvents is likely due to the increasing strength of dye-dye interactions with decreasing values of d (discussed below) rather than a failure of the system to reach equilibrium.
Short-range interactions similarly affected the relaxation behavior of C (κ2, κ2, τ) for d = 2.0 nm, which converged weakly relative to data for larger values of d. For d ≥ 3 nm, C (κ2, κ2, τ) gave single-exponential decay times between 100 and 175 ps (Fig. S2). These relaxation times are semiquantitatively consistent but slightly larger than those obtained by Deplazes et al. (40) for untethered Alexa dyes, which have smaller ring systems than the dyes examined in this study. As noted in Materials and Methods, force-field parameterization is a critical determinant of simulation accuracy in any MD study. At present, standard parameterization techniques, such as those used here, do not fully take into account important phenomena such as molecular polarizability. The dye dynamics observed here are reassuringly consistent with previous results; however, it remains to be shown that a similar consistency holds in the case of more sophisticated parameterization schemes.
Also, there appears to be a negligible cross correlation of R and κ2 (Fig. S3), which validates the use of Eq. 2 as discussed in Deplazes et al. (40). The relaxation times for C (κ2, κ2, τ) are significantly smaller than the anisotropy decay times of individual dyes in the tethered-dye simulations, which are in the range of 500 ps in water and 1.5 ns in glycerol/water (Fig. S5). The dependence of anisotropy decay times on solvent conditions exactly follows the increment in bulk solvent viscosity (56).
Solvent effects on the tethered fluorophore-linker conformation
Linker groups tethering the fluorophores are expected to be highly flexible. Nonetheless, we find that dye-linker interactions can potentially restrict fluorophore motion. The structure of the ATTO 610/linker moiety in aqueous simulations with d = 4.0 nm alternated between the two conformations shown in Fig. 4, i.e., a fully extended form and a U-shaped conformation. Because this tethering distance is large enough for the dyes to exert a minimal influence on each other, the U-shaped conformation may possibly be stabilized by hydrophobic interactions between the dye and linker. Aqueous conditions slightly favor the U shape (56:44 U-shaped: extended), whereas solvation in glycerol/water inverts this ratio (44:56 U-shaped: extended). This difference in conformational bias evidently has negligible effects on <κ2(t)>T, which had similar values for both solvents (Fig. 3 B). The ATTO 647N linker was predominantly folded into the hairpin structure shown in Fig. 4 D independently of the solvent conditions. This is probably due to the sterically preferred orthogonal orientation of the linker-conjugated, six-membered ring relative to the plane of the main hexacyclic group in the fluorophore (see Movie S1).
Figure 4.
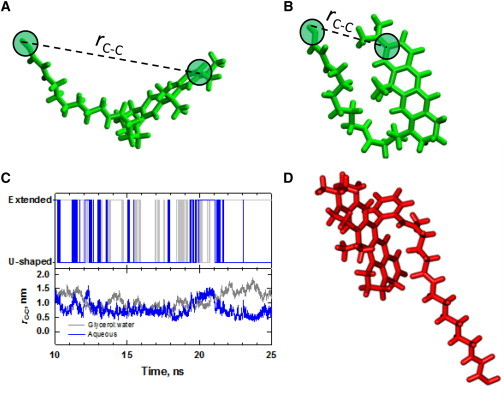
Conformational states of linker-conjugated fluorophores. (A) Extended and (B) U-shaped conformations of the ATTO 610-linker conjugate. This conformational equilibrium can be characterized by examining fluctuations of the distance between the designated carbon atoms, rC−C. (C) Behavior of rC−C over a 15 ns window in aqueous (blue) and glycerol/water (gray) simulations. The lower panel shows the actual time dependence of rC−C, and the upper panel is the result of a binary classifier applied to the continuous rC−C distribution. Here, the dye/linker conformation was scored as extended if rC−C ≥ 1 nm and U-shaped otherwise. (D) Time-averaged structure of linker-conjugated ATTO 647. (Two columns, 6.50″ W × 5.24″ H.) To see this figure in color, go online.
Pair-distance distributions for tethered fluorophores
This MD study was motivated in part by the previous use of simplified models for calculating spatial distributions of fluorophores based on SA (34,35). As discussed above, SA models contain many assumptions, not the least of which is that the dyes interact with one another and with macromolecular components only through hard-sphere repulsive interactions. Possible attractive forces between dyes and other species are not normally considered. We hypothesized that these assumptions needed verification, especially in the case of experiments where details of dye-dye interactions might be altered by solvation conditions.
Previous Cre-mediated DNA synapsis experiments used mixed-solvent buffer conditions to obtain measurable levels of intermolecular Cre recombination (42). The buffer in question consists of 25 mM N-Tris[hydroxymethyl]methyl-3-aminopropanesulfonic acid (TAPS), 180 mM NaCl, and 2 mM MgCl2 plus significant concentrations of glycerol, PEG, and bovine serum albumin (BSA) (55). It is not practical to introduce additional high-molecular-weight species such as PEG and BSA into simulations of systems as large as a Cre-DNA synapse; thus, we sought to approximate the effect of these species on the buffer dielectric constant in the simulation by using a binary mixture of glycerol and water as the solvent. This mixture, which has a glycerol mole fraction of 0.39, yields a bulk dielectric constant similar to that of the original buffer solution used in the recombination experiments (42,55). We compensated for the longer dye correlation times in glycerol/water relative to aqueous conditions (see above) by extending the duration of the mixed-solvent trajectories well beyond those of corresponding aqueous simulations. Thus, the minimum duration of the glycerol/water trajectories for any of the systems studied here was 100 ns.
We found radical differences in the dye-pair distance-distribution functions obtained for MD simulations of tethered fluorophores carried out in water and in glycerol/water, as shown in Fig. 5. Notably, none of the MD distributions bore any resemblance to the near-Gaussian distribution computed using an MC-based SA calculation as described in Shoura et al. (42). Whereas a clear propensity for the dyes to form attractive interactions exists in the aqueous case, there is a measureable tendency for the dyes to repel each other in water/glycerol. Such effects are not taken into account in the MC model; moreover, solvent effects are present in the simulation over a range of separations, d, from 2.0 nm to at least 4.0 nm. The most plausible explanation for the solvent dependence is that dye-dye interactions are mainly driven by hydrophobic forces in aqueous media. The reduced dielectric shielding in glycerol/water mixtures increases the strength of charge-charge interactions. Because both dyes have a single negative charge under these simulation conditions, Coulombic interactions became the dominant force, leading to a net dye-dye repulsion that is not observed in the aqueous case.
Figure 5.
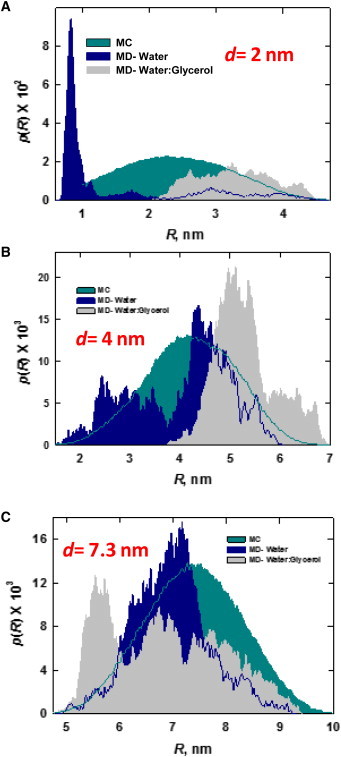
Dye-pair distance-distribution functions for tethered fluorophores as a function of d in aqueous (blue) and glycerol/water (gray) MD simulations. Results of MC SA calculations are shown for comparison in green. Post hoc statistical analysis using the ANOVA/Tukey method yields p < 0.05 for pairwise comparisons of all of the distributions in A and B. Based on this analysis, we can conclude that the differences in SA, MD (aqueous), and MD (glycerol/water) distance distributions for tethered ATTO dyes where d ≤ 4 nm are statistically significant. Differences in the distributions in C, where d = 7.3 nm, are not statistically significant, p = 0.48). (One column, 3.25″W × 6.95″H.) To see this figure in color, go online.
The dependence of <R(t)>T, <κ2(t)>T, and <E(t)>T as a function of tethering distance d is shown for both solvents and also compared with MC values for <R> and <E> in Fig. 6. Note that <E(t)>T is computed from values of R(t) and κ2(t) for each frame. Although this approach is not rigorously correct due to conformational fluctuations that can occur during the lifetime of the donor excited state (41,57), it permits comparisons between a model that takes into account detailed interactions on the atomic scale with simple SA-based models.
Figure 6.
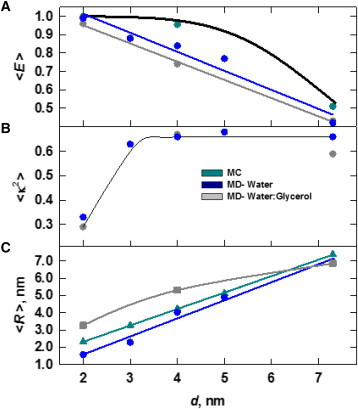
Behavior of <R(t)>T, <κ2(t)>T, and <E(t)>T for tethered ATTO dyes as a function of distance d in aqueous (blue data points) and glycerol/water (gray data points) MD simulations and for the SA model (green data points). The dependence of <E(t)>T on R (Eq. 1, black curve) for R0 = 7.3 nm is in good agreement with the SA data. The middle panel gives the dependence of <κ2(t)>T on d for MD simulations in aqueous and glycerol/water solvent systems; these data are identical to those in Fig. 3B. The bottom panel shows the dependence of <R(t)>T on d. For large values of d (d = 7.3 nm), the effects of solvent on <R(t)>T and <E(t)>T are negligible. Error bars corresponding to ±1 SE are smaller than the data points. (One column, 3.25″ W × 3.89″ H.) To see this figure in color, go online.
As discussed above, the value of <κ2> is not dramatically affected by solvent conditions; we find that <κ2> assumes its isotropic value of 0.67 for all but the smallest value of d investigated (Fig. 6, middle panel). However, there is a systematic trend in the average through-space separation of the dyes, <R>, which is reflected in the computed energy-transfer efficiency <E>. Being largely hydrophobic, interactions of the dye with the less-polar solvent are favored, accompanied by attenuated dye-dye interactions.
For the case in which d = 4.0 nm (Fig. 6 B), <R> for glycerol/water simulations is significantly larger than the value of <R> obtained in aqueous conditions, leading to a reduction in <E> from 0.84 to 0.74. We also note that in the regime where <κ2> deviates significantly from 0.67, <E> is highly insensitive to <κ2>. This is expected to be true for most systems in which the average dye-dye distance is small compared with the isotropic value of R0.
Rotational dynamics of dyes conjugated to DNA and protein-DNA complexes
We carried out MD simulations on protein-DNA complexes based on crystallographic structures available for the Cre antiparallel synapse (PDB: 5CRX) and the Cre-HJ (PDB: 3CRX). Three different DNA structures (loxP duplex, system 2), Cre-loxP synapse (system 3), and Cre-loxP HJ (system 4) (see Fig. 7) were simulated with dyes conjugated to positions corresponding to the locations of the donor and acceptor fluorophores in the putative intermediates and recombination product generated in Shoura et al. (42). Furthermore, we took the mechanistic cleavage-pattern distribution of Cre (58) into account by investigating two distinct strand-cleavage scenarios for each of the Cre synapse and HJ structures. Based on previous experimental studies (45,46,58), we expect that 80% of the complexes are scenario 1 (GC-cleavage) complexes. A minority (20%) of complexes are generated via AT cleavage, which we denote the scenario 2 complex (58). Table 1 shows that the <κ2> value for conjugated dyes in all of these models deviates from the isotropic value of 2/3. This is clearly due to the restricted mobility of the conjugated ATTO dyes, which is also the case for the duplex DNA recombination product (24,39).
Figure 7.
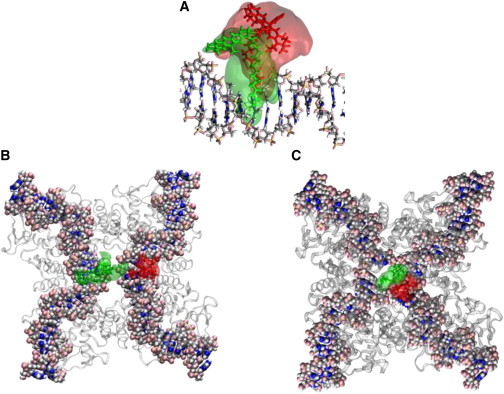
ATTO-DNA systems simulated by MD in the course of this work. (A) DNA duplex modeling the product of the Cre-recombination reaction in (42), in which donor and acceptor fluorophores are conjugated to C5 positions of adjacent thymine residues on opposing strands. (B) A fluorophore-labeled Cre-mediated synapse of DNA duplexes based on the PDB cocrystal structure 5CRX (46,60). (C) The Cre HJ intermediate complex based on the PDB cocrystal structure 3CRX (45,46,60) with fluorophore labels at sites corresponding to the positions used in Shoura et al. (42). Integrated positions of donor (green) and acceptor (red) centers of mass over the course of complete trajectories in aqueous solution are shown. See also Movie S2. (Two columns, 6.5″ W × 5.19″ H.) To see this figure in color, go online.
Table 1.
Values of <κ2(t)>T and <E(t)> for different MD simulations in this study
| System | Solvent | <κ2(t)>T, (± σ∗) | <E(t)> |
|---|---|---|---|
| 5CRX: antiparallel Cre-DNA synaptic complex | aqueous | 0.71 (± 0.13) | 0.98 |
| 5CRX: parallel Cre-DNA synaptic complex | aqueous | 1.17 (± 0.16) | 0.98 |
| 3CRX: Cre-DNA Holliday junction intermediate (scenario 1) | aqueous | 0.28 (± 0.03) | 0.99 |
| 3CRX: Cre-DNA Holliday junction intermediate (scenario 1) | water/glycerol | 0.12 (± 0.02) | 0.96 |
| 3CRX: Cre-DNA Holliday junction intermediate (scenario 2) | aqueous | 0.70 (± 0.12) | 0.99 |
| LoxP duplex | aqueous | 0.36 (± 0.04) | 0.99 |
Lower-bound uncertainties, which were obtained by block averaging (see Fig. S1), are given as ±1 SE (±σ∗).
Differences between MD and experimental FRET efficiencies for the Cre-HJ complex
Previous studies support the notion that the Cre-HJ intermediate is the longest-lived intermediate in the Cre recombination pathway (42,55,59). We therefore focused on the solvent dependence of dye dynamics in the HJ Cre-DNA (PDB: 3CRX) structure. Fig. 8 shows the MD dye-distance distributions for the labeled HJ Cre-DNA complex in water and glycerol/water along with the MC-simulated distribution for the same structure. Clearly, the MD distributions obtained for both solvent systems are radically different from the MC results. Moreover, the same trend in the solvent-dependent MD distance distributions observed in the case of tethered dyes, namely, a larger value of <R> in glycerol/water versus aqueous 0.2 M NaCl, is recapitulated here. Thus, we conclude that repulsive forces between the ATTO dyes dominate the dye-distance distribution in glycerol/water even within the highly restricted environment of the protein-bound HJ. By comparing the present simulation results with experimental results reported in Shoura et al. (42) for the Cre synaptic complex (E = 0.88), we find that the relative reduction in <E> for glycerol/water (0.96) versus aqueous MD simulations (0.99) amounts to about half of the discrepancy between the experimental E (0.88) and the SA/MC value of 0.99 expected for isotropically averaged fluorophores tethered to the crystallographic Cre-HJ intermediate.
Figure 8.
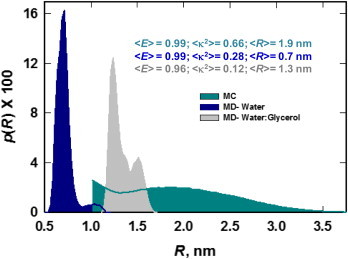
Distance distributions for fluorophores in the DNA-Cre HJ (see Fig. 7C). The MD distributions were computed from aqueous (blue) and glycerol/water (gray) MD simulations; MC SA results are shown in green. The cutoff in the SA results at 1 nm is due to the treatment of donor and acceptor dyes as 1-nm-diameter hard spheres. Post hoc ANOVA/Tukey statistical analysis of pairs of distributions gave confidence intervals of p < 0.05 for all pairs, indicating that differences among the distributions are statistically significant. (One column, 3.25″ W × 2.47″ H.) To see this figure in color, go online.
This small but possibly significant difference (see Fig. 8) points to a potential role of solvent conditions in attenuating energy transfer between dyes. However, we cannot completely rule out the possibility that other factors that were not captured by the MD simulations may have contributed to the experimentally observed E value. These include geometric distortion of the Cre-HJ intermediate relative to its crystallographic structure and/or differences between the proxy dye ATTO 610 and the actual dye used in the experiments (ATTO 594). Thus, a reevaluation of the solvent-dependent interactions between donor and acceptor may be needed when the ATTO 594 structure becomes available. Finally, trajectories approaching a 200 ns duration, which are limited by the size of these systems, are likely still far short of the timescale that is involved in conformational rearrangements of the complex.
Conclusions
Under the right conditions, the distance dependence of energy transfer in FRET experiments is a powerful tool for investigating macromolecular structure and interactions. When donor-acceptor dye pairs are sufficiently close to one another (R << R0), FRET is a reliable reporter of probe-probe proximity because energy transfer depends weakly on the orientation factor, κ2. We exploited this lack of sensitivity in previous studies of the Cre-loxP recombination system (42), in which we used FRET as a binary reporter of the probe-pair distance.
It is challenging to interpret measured energy-transfer efficiency values in terms of fluorophore-fluorophore distances in an intermediate distance regime, not least because of common failure of the isotropic rotation assumption. Many modeling approaches for estimating <R> from <E> rely on probe distributions computed from SA (2,33–35). However, our work suggests that when taking realistic dye properties into account, one should consider that the dye-dye, dye-solvent, and dye-macromolecule interactions make significant contributions to the spatial and orientational distributions of these probes. This conclusion suggests that the use of realistic MD-based modeling incorporating details such as solvent composition can be a powerful adjunct to experimental design strategies for choosing the location and chemical environment of fluorescent probes in future FRET studies. Indeed, it is possible that the FRET experiments in Shoura et al. (42) could have been more highly optimized to extract structural information about the Cre synaptic complex if MD-based modeling results had been available in advance. Ideally, iterative cycles of simulation, experimental design, and laboratory measurements can be a highly effective approach for FRET-based studies of complex macromolecular structures.
Acknowledgments
We thank Stefan Giovan and Blake Wilson for helpful discussions. The use of the High-Performance Computing resources of the Texas Advanced Computing Center at The University of Texas at Austin is gratefully acknowledged.
This work was supported by grants from the National Institutes of Health /National Science Foundation Joint Program in Mathematical Biology (DMS-0800929 to S.D.L.), the SRC Engineering Research Center (to S.O.N.), and the UK Biotechnology and Biological Sciences Research Council (BB/1019294/1 to S.A.H.).
Supporting Material
References
- 1.Mitra R.D., Silva C.M., Youvan D.C. Fluorescence resonance energy transfer between blue-emitting and red-shifted excitation derivatives of the green fluorescent protein. Gene. 1996;173:13–17. doi: 10.1016/0378-1119(95)00768-7. [DOI] [PubMed] [Google Scholar]
- 2.Treutlein B., Muschielok A., Michaelis J. Dynamic architecture of a minimal RNA polymerase II open promoter complex. Mol. Cell. 2012;46:136–146. doi: 10.1016/j.molcel.2012.02.008. [DOI] [PubMed] [Google Scholar]
- 3.Day R.N. Visualization of Pit-1 transcription factor interactions in the living cell nucleus by fluorescence resonance energy transfer microscopy. Mol. Endocrinol. 1998;12:1410–1419. doi: 10.1210/mend.12.9.0168. [DOI] [PubMed] [Google Scholar]
- 4.McKinney S.A., Freeman A.D., Ha T. Observing spontaneous branch migration of Holliday junctions one step at a time. Proc. Natl. Acad. Sci. USA. 2005;102:5715–5720. doi: 10.1073/pnas.0409328102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tan E., Wilson T.J., Ha T. A four-way junction accelerates hairpin ribozyme folding via a discrete intermediate. Proc. Natl. Acad. Sci. USA. 2003;100:9308–9313. doi: 10.1073/pnas.1233536100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bussiek M., Tóth K., Langowski J. Trinucleosome compaction studied by fluorescence energy transfer and scanning force microscopy. Biochemistry. 2006;45:10838–10846. doi: 10.1021/bi060807p. [DOI] [PubMed] [Google Scholar]
- 7.Singleton S.F., Xiao J. The stretched DNA geometry of recombination and repair nucleoprotein filaments. Biopolymers. 2001-2002;61:145–158. doi: 10.1002/bip.10145. [DOI] [PubMed] [Google Scholar]
- 8.Förster T. Experimental and theoretical investigation of the intermolecular transfer of electronic excitation energy. Z. Naturforsch. A. 1949;4:321–327. [Google Scholar]
- 9.Miick S.M., Fee R.S., Chazin W.J. Crossover isomer bias is the primary sequence-dependent property of immobilized Holliday junctions. Proc. Natl. Acad. Sci. USA. 1997;94:9080–9084. doi: 10.1073/pnas.94.17.9080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wozniak A.K., Schröder G.F., Oesterhelt F. Single-molecule FRET measures bends and kinks in DNA. Proc. Natl. Acad. Sci. USA. 2008;105:18337–18342. doi: 10.1073/pnas.0800977105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Margittai M., Widengren J., Seidel C.A. Single-molecule fluorescence resonance energy transfer reveals a dynamic equilibrium between closed and open conformations of syntaxin 1. Proc. Natl. Acad. Sci. USA. 2003;100:15516–15521. doi: 10.1073/pnas.2331232100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ha T., Kozlov A.G., Lohman T.M. Single-molecule views of protein movement on single-stranded DNA. Annu. Rev. Biophys. 2012;41:295–319. doi: 10.1146/annurev-biophys-042910-155351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tomschik M., van Holde K., Zlatanova J. Nucleosome dynamics as studied by single-pair fluorescence resonance energy transfer: a reevaluation. J. Fluoresc. 2009;19:53–62. doi: 10.1007/s10895-008-0379-1. [DOI] [PubMed] [Google Scholar]
- 14.Bönisch C., Schneider K., Hake S.B. H2A.Z.2.2 is an alternatively spliced histone H2A.Z variant that causes severe nucleosome destabilization. Nucleic Acids Res. 2012;40:5951–5964. doi: 10.1093/nar/gks267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.White C.L., Luger K. Defined structural changes occur in a nucleosome upon Amt1 transcription factor binding. J. Mol. Biol. 2004;342:1391–1402. doi: 10.1016/j.jmb.2004.07.080. [DOI] [PubMed] [Google Scholar]
- 16.Gell C., Sabir T., Stockley P.G. Single-molecule fluorescence resonance energy transfer assays reveal heterogeneous folding ensembles in a simple RNA stem-loop. J. Mol. Biol. 2008;384:264–278. doi: 10.1016/j.jmb.2008.08.088. [DOI] [PubMed] [Google Scholar]
- 17.Muñoz-Losa A., Curutchet C., Mennucci B. Fretting about FRET: failure of the ideal dipole approximation. Biophys. J. 2009;96:4779–4788. doi: 10.1016/j.bpj.2009.03.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chang J.C. Monopole effects on electronic excitation interactions between large molecules. I. Applications to energy transfer in chlorophylls. J. Chem. Phys. 1977;67:3901. [Google Scholar]
- 19.Krueger B.P., Scholes G.D., Fleming G.R. Calculation of couplings and energy transfer pathways between the pigments of LH2 by the ab initio transition density cube method. J. Phys. Chem. B. 1998;102:5378–5386. [Google Scholar]
- 20.Dale R.E., Eisinger J., Blumberg W.E. The orientational freedom of molecular probes. The orientation factor in intramolecular energy transfer. Biophys. J. 1979;26:161–193. doi: 10.1016/S0006-3495(79)85243-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Badali D., Gradinaru C.C. The effect of Brownian motion of fluorescent probes on measuring nanoscale distances by Förster resonance energy transfer. J. Chem. Phys. 2011;134:225102. doi: 10.1063/1.3598109. [DOI] [PubMed] [Google Scholar]
- 22.Dale R.E., Eisinger J. Intramolecular distances determined by energy transfer. Dependence on orientational freedom of donor and acceptor. Biopolymers. 1974;13:1573–1605. [Google Scholar]
- 23.Allen L.R., Paci E. Orientational averaging of dye molecules attached to proteins in Förster resonance energy transfer measurements: insights from a simulation study. J. Chem. Phys. 2009;131:065101. doi: 10.1063/1.3193724. [DOI] [PubMed] [Google Scholar]
- 24.Ouellet J., Schorr S., Lilley D.M. Orientation of cyanine fluorophores terminally attached to DNA via long, flexible tethers. Biophys. J. 2011;101:1148–1154. doi: 10.1016/j.bpj.2011.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Van der Meer B.W. John Wiley & Sons, Ltd.; London: 1999. Orientational Aspects in Pair Energy Transfer. [Google Scholar]
- 26.Dale R.E., Eisinger J. Intramolecular energy transfer and molecular conformation. Proc. Natl. Acad. Sci. USA. 1976;73:271–273. doi: 10.1073/pnas.73.2.271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Loura L.M. Simple estimation of Forster resonance energy transfer (FRET) orientation factor distribution in membranes. Int. J. Mol. Sci. 2012;13:15252–15270. doi: 10.3390/ijms131115252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hoefling M., Grubmuller H. In silico FRET from simulated dye dynamics. Comput. Phys. Commun. 2013;184:841–852. [Google Scholar]
- 29.VanBeek D.B., Zwier M.C., Krueger B.P. Fretting about FRET: correlation between kappa and R. Biophys. J. 2007;92:4168–4178. doi: 10.1529/biophysj.106.092650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ranjit S., Gurunathan K., Levitus M. Photophysics of backbone fluorescent DNA modifications: reducing uncertainties in FRET. J. Phys. Chem. B. 2009;113:7861–7866. doi: 10.1021/jp810842u. [DOI] [PubMed] [Google Scholar]
- 31.Ivanov V., Li M., Mizuuchi K. Impact of emission anisotropy on fluorescence spectroscopy and FRET distance measurements. Biophys. J. 2009;97:922–929. doi: 10.1016/j.bpj.2009.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Rothwell P.J., Berger S., Seidel C.A. Multiparameter single-molecule fluorescence spectroscopy reveals heterogeneity of HIV-1 reverse transcriptase:primer/template complexes. Proc. Natl. Acad. Sci. USA. 2003;100:1655–1660. doi: 10.1073/pnas.0434003100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sindbert S., Kalinin S., Seidel C.A. Accurate distance determination of nucleic acids via Förster resonance energy transfer: implications of dye linker length and rigidity. J. Am. Chem. Soc. 2011;133:2463–2480. doi: 10.1021/ja105725e. [DOI] [PubMed] [Google Scholar]
- 34.Muschielok A., Andrecka J., Michaelis J. A nano-positioning system for macromolecular structural analysis. Nat. Methods. 2008;5:965–971. doi: 10.1038/nmeth.1259. [DOI] [PubMed] [Google Scholar]
- 35.Muschielok A., Michaelis J. Application of the nano-positioning system to the analysis of fluorescence resonance energy transfer networks. J. Phys. Chem. B. 2011;115:11927–11937. doi: 10.1021/jp2060377. [DOI] [PubMed] [Google Scholar]
- 36.Milas P., Gamari B.D., Goldner L.S. Indocyanine dyes approach free rotation at the 3′ terminus of A-RNA: a comparison with the 5′ terminus and consequences for fluorescence resonance energy transfer. J. Phys. Chem. B. 2013;117:8649–8658. doi: 10.1021/jp311071y. [DOI] [PubMed] [Google Scholar]
- 37.Spiriti J., Binder J.K., van der Vaart A. Cy3-DNA stacking interactions strongly depend on the identity of the terminal basepair. Biophys. J. 2011;100:1049–1057. doi: 10.1016/j.bpj.2011.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Corry B., Jayatilaka D. Simulation of structure, orientation, and energy transfer between AlexaFluor molecules attached to MscL. Biophys. J. 2008;95:2711–2721. doi: 10.1529/biophysj.107.126243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Iqbal A., Arslan S., Lilley D.M. Orientation dependence in fluorescent energy transfer between Cy3 and Cy5 terminally attached to double-stranded nucleic acids. Proc. Natl. Acad. Sci. USA. 2008;105:11176–11181. doi: 10.1073/pnas.0801707105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Deplazes E., Jayatilaka D., Corry B. Testing the use of molecular dynamics to simulate fluorophore motions and FRET. Phys. Chem. Chem. Phys. 2011;13:11045–11054. doi: 10.1039/c1cp20447e. [DOI] [PubMed] [Google Scholar]
- 41.Hoefling M., Lima N., Grubmüller H. Structural heterogeneity and quantitative FRET efficiency distributions of polyprolines through a hybrid atomistic simulation and Monte Carlo approach. PLoS ONE. 2011;6:e19791. doi: 10.1371/journal.pone.0019791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Shoura M.J., Vetcher A.A., Levene S.D. Measurements of DNA-loop formation via Cre-mediated recombination. Nucleic Acids Res. 2012;40:7452–7464. doi: 10.1093/nar/gks430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zarrabi N., Ernst S., Börsch M. Analyzing conformational dynamics of single P-glycoprotein transporters by Förster resonance energy transfer using hidden Markov models. Methods. 2014;66:168–179. doi: 10.1016/j.ymeth.2013.07.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Thévenin D., Lazarova T. Identifying and measuring transmembrane helix-helix interactions by FRET. Methods Mol. Biol. 2012;914:87–106. doi: 10.1007/978-1-62703-023-6_6. [DOI] [PubMed] [Google Scholar]
- 45.Guo F., Gopaul D.N., van Duyne G.D. Structure of Cre recombinase complexed with DNA in a site-specific recombination synapse. Nature. 1997;389:40–46. doi: 10.1038/37925. [DOI] [PubMed] [Google Scholar]
- 46.Guo F., Gopaul D.N., Van Duyne G.D. Asymmetric DNA bending in the Cre-loxP site-specific recombination synapse. Proc. Natl. Acad. Sci. USA. 1999;96:7143–7148. doi: 10.1073/pnas.96.13.7143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Phillips J.C., Braun R., Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.MacKerell A.D., Jr., Banavali N., Foloppe N. Development and current status of the CHARMM force field for nucleic acids. Biopolymers. 2000-2001;56:257–265. doi: 10.1002/1097-0282(2000)56:4<257::AID-BIP10029>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- 49.Hoover W.G. Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A. 1985;31:1695–1697. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- 50.Flyvbjerg H., Petersen H. Error estimates on average of correlated data. J. Chem. Phys. 1989;91:461–466. [Google Scholar]
- 51.Hill T.L. McGraw Hill; New York: 1956. Statistical Mechanics. Principles and Selected Applications. [Google Scholar]
- 52.Lopes P.E.M., Roux B., Mackerell A.D., Jr. Molecular modeling and dynamics studies with explicit inclusion of electronic polarizability. Theory and applications. Theor. Chem. Acc. 2009;124:11–28. doi: 10.1007/s00214-009-0617-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lin H., Truhlar D. QM/MM: what have we learned, where are we, and where do we go from here? Theor. Chem. Acc. 2007;177:185–199. [Google Scholar]
- 54.Egorov A.V., Lyubartsev A.P., Laaksonen A. Molecular dynamics simulation study of glycerol-water liquid mixtures. J. Phys. Chem. B. 2011;115:14572–14581. doi: 10.1021/jp208758r. [DOI] [PubMed] [Google Scholar]
- 55.Ringrose L., Lounnas V., Stewart A.F. Comparative kinetic analysis of FLP and cre recombinases: mathematical models for DNA binding and recombination. J. Mol. Biol. 1998;284:363–384. doi: 10.1006/jmbi.1998.2149. [DOI] [PubMed] [Google Scholar]
- 56.Shankar P.N., Kumar M. Experimental Determination of the Kinematic Viscosity of Glycerol-Water Mixtures. Proc. R. Soc. Lond., A. 1994;444:573–581. [Google Scholar]
- 57.Speelman A.L., Muñoz-Losa A., Krueger B.P. Using molecular dynamics and quantum mechanics calculations to model fluorescence observables. J. Phys. Chem. A. 2011;115:3997–4008. doi: 10.1021/jp1095344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Lee L., Sadowski P.D. Identification of Cre residues involved in synapsis, isomerization, and catalysis. J. Biol. Chem. 2003;278:36905–36915. doi: 10.1074/jbc.M305464200. [DOI] [PubMed] [Google Scholar]
- 59.Vetcher A.A., Lushnikov A.Y., Levene S.D. DNA topology and geometry in Flp and Cre recombination. J. Mol. Biol. 2006;357:1089–1104. doi: 10.1016/j.jmb.2006.01.037. [DOI] [PubMed] [Google Scholar]
- 60.Gopaul D.N., Guo F., Van Duyne G.D. Structure of the Holliday junction intermediate in Cre-loxP site-specific recombination. EMBO J. 1998;17:4175–4187. doi: 10.1093/emboj/17.14.4175. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


