Equilibrium Conformations of Concentric-tube Continuum Robots

Abstract

Robots consisting of several concentric, preshaped, elastic tubes can work dexterously in narrow, constrained, and/or winding spaces, as are commonly found in minimally invasive surgery. Previous models of these “active cannulas” assume piecewise constant precurvature of component tubes and neglect torsion in curved sections of the device. In this paper we develop a new coordinate-free energy formulation that accounts for general preshaping of an arbitrary number of component tubes, and which explicitly includes both bending and torsion throughout the device. We show that previously reported models are special cases of our formulation, and then explore in detail the implications of torsional flexibility for the special case of two tubes. Experiments demonstrate that this framework is more descriptive of physical prototype behavior than previous models; it reduces model prediction error by 82% over the calibrated bending-only model, and 17% over the calibrated transmissional torsion model in a set of experiments.

1. Introduction

An active cannula is a continuum robot consisting of concentric elastic tubes, each of which has a preset curved shape (see Figure 1). This thin continuum robot design is mechanically simple, and has the ability to reach dexterously into confined or winding environments (Webster et al. 2009). The tubes of the cannula form a single “backbone” that elastically changes shape as they translate and rotate axially. Transmitting moments within the backbone in this way provides an alternative to prior continuum robot designs that use support disks with tendon wires (Dario et al. 2000; Hannan and Walker 2003), elastic sleeves with embedded tendons (Camarillo et al. 2008), flexible push rods (Simaan et al. 2004), or pneumatic actuators (Chirikjian 1995; Jones et al. 2006) to apply bending moments. Despite its mechanical simplicity, computing equilibrium conformations of an active cannula (i.e. the forward kinematics problem) remains a challenge.

Fig. 1.

A prototype active cannula made of four superelastic Nitinol tubes and one central wire (with three tubes and the wire visible).

The idea of deriving dexterity from counter-rotated, precurved concentric tubes was introduced relatively recently. Note that the kinematic conditioning of larger scale robot manipulators (with complex linkages, cabling, and actuation) will typically exceed that of active cannulas, so in the present context “dexterity” simply describes the affordance of multiple degrees of freedom at the tip given only basal actuation. Loser (2002) developed a steerable needle composed of two fully overlapping precurved cannulas whose bases rotate (but do not translate) relative to one another to change needle curvature. Daum (2003) patented a deflectable needle assembly in which a curved “catheter” is deployed through a rigid outer cannula. A similar system is the “Curved Multi-Tube” (CMT) of Furusho et al. (2006), where the tubes do not translate, but are constructed such that a portion of the inner tube lies beyond the end of the outer (Terayama et al. 2007). Initial CMT models required infinite flexural rigidity of every outer tube with respect to the collection of smaller tubes inside it, and infinite torsional rigidity of all tubes.

Recently, the more general active cannula mechanism—telescoping, concentric tubes that both translate and rotate with respect to one another—has emerged, along with beam mechanics models that account for flexural and (limited) torsional elasticity (Webster et al. 2006b; Sears and Dupont 2006, 2007; Webster et al. 2008, 2009). Assuming piecewise-constant precurvature and torsional rigidity in curved sections, these models describe active cannula backbone shape by balancing moments between component tubes. Under these assumptions, the resulting active cannula shape is comprised of a finite sequence of mutually tangent circular arcs.

This new actuation strategy appears to be well suited for applications at the “meso-scale” (≈ 0.1–100 mm) that require thin, dexterous manipulators, including minimally invasive surgical procedures. Specific applications for which active cannulas have been proposed include accessing the lung via the throat (Webster et al. 2008, 2009), transgastric surgery (Webster et al. 2006b), fetal procedures (Furusho et al. 2006), steering needles embedded in tissue (Loser 2002; Sears and Dupont 2006), cardiac procedures (Sears and Dupont 2006), and transnasal skull base access (Webster et al. 2006b). An overview of several specific ways active cannulas might be used in medicine is given in Webster (2007). It is also possible in principle to construct very small active cannulas which may be useful in cell manipulation (Sun and Nelson 2002; Kumar et al. 2003; Ediz and Olgac 2004) and other microsurgical applications. In some of the above applications (e.g. lung), active cannulas will be used in air-filled cavities, and thus the free-space cannula models developed in this paper will apply directly.

When the cannula is embedded in tissue (e.g. when used as a steerable needle), a free-space kinematic model will need to be coupled to a tissue model to predict cannula shape, as has been done for straight needles (Alterovitz et al. 2003; DiMaio and Salcudean 2005; Glozman and Shoham 2007). When used as steerable needles in the tissue embedded case, active cannulas will have both benefits and drawbacks when compared with tip-based steering techniques that utilize tissue interaction forces to steer (Okazawa et al. 2005; Webster et al. 2006a). Benefits include the potential to manipulate tissue intentionally using cannula shaft shape change, and the ability to leave one soft-tissue medium, traverse open space, and enter another. Potential drawbacks include increased complexity of control and the fact that cannula preshaping may impose restrictions on achievable shapes within tissue to which tip-steered needles are not subject. Independent of whether an active cannula is used in tissue or free space (e.g. in the lung), the first step in practical implementation is being able to predict cannula shape in free space as a function of axial rotations and translations of the component tubes, the “joint variables” of the robot.

Prior models neglect torsional effects in curved sections, but a recent model incorporating torsional effects in straight sections of the device (Webster et al. 2006b, 2009) demonstrates the critical role of torsion in describing categorical features of the energy landscape, as well as in accurately predicting tip position (Webster et al. 2008, 2009). For the specific experimental setup reported by Webster et al. (2009), this model predicts the location of the cannula end point with an average accuracy of 3.0 mm. However, the difference between predicted and experimental cannula tip positions is not uniform over the workspace, and is worst (8.76 mm) near the workspace boundary. Moreover, in this region, the model of Webster et al. (2009) indicates that torsion in the straight section is at its highest. This suggests that, although neglected by this “lumped-parameter” model, there may be high torsional moments in the curved sections. Support for this was found in the first model that accounted for torsion in curved sections of a two-tube cannula with circular precurvatures, an initial version of which is available in Rucker and Webster (2008), and an enhanced presentation of which can be found in Section 4. A subsequent presentation of the closed-form two-tube solution appeared in Dupont et al. (2009). Derivation of the multi-tube case with variable curvature and torsion that we present in this paper has also been developed concurrently and independently and presented simultaneously in Rucker and Webster (2009a) and Dupont et al. (2009), where different analytical methods are applied to achieve the same final equations. Thus, it has come to be known that torsion in curved sections is a significant phenomenon that should be modeled. This motivates the generalized free-space model we present in this paper, which accounts for both bending and torsion throughout a multi-tube cannula, and enables use of cannulas incorporating variable precurvature.

Significant progress toward such a general model for wire-driven continuum robots with a single flexible backbone has been made in recent years. A general formulation for the energy stored in a deformed elastic backbone is given and minimized using variational calculus in Chirikjian and Burdick (1995), and used for wire driven continuum robots in Gravagne and Walker (2000) and Gravagne (2002). In this paper, we adopt a similar strategy to describe the equilibrium conformations of multiple precurved concentric tubes. Other recent related work has considered slender beam deformation from a group theoretic perspective (Selig and Ding 2001). There, a model was derived that can predict beam deflection due to an applied wrench, which reduces in the 2D pure bending case to classical results. This work shows the feasibility of approaching beam mechanics problems via group theory.

In this paper, we present a coordinate-free formulation for the energy stored within an active cannula. With arc length (rather than time) taken as the independent variable, the stored elastic energy in the backbone is analogous to the kinetic energy of a free rigid body. This formulation explicitly accounts for both bending and torsion throughout the cannula. It also accounts for general (non-circular) precurvatures of component tubes. We present several specific examples that illustrate how the Euler–Lagrange and Euler–Poincaré equations can be applied to derive a set of differential equations, a solution to which corresponds to the minimum energy conformation of the cannula.

Furthermore, we show that, with appropriate assumptions, our formulation includes prior models as special cases. We also present an analysis of the shape of curved, concentric tubes under both bending and torsion, deriving an analytical solution for the two-tube case, and demonstrating that the resultant cannula shape will be non-circular. The experimental contribution of this paper is a demonstration that the new modeling framework can reduce model prediction error by 82% over the prior bending-only model, and 17% over the prior transmissional torsion model in a simple set of experiments with a prototype active cannula. These results were obtained with calibrated model parameters in all three cases.

2. Formulating the Energy Functional

We begin by formulating an energy functional which describes the total elastic energy due to bending and torsion stored in all tubes of a general n-tube cannula. We first provide a convention for describing the curves which define the shape of the individual tubes and the overall cannula shape. We then describe the total elastic (strain) energy stored in a single tube. The general energy functional can then be obtained by summing these individual tube energies.

2.1. Assumptions

The energy formulation in this section is performed under the standard assumptions of Kirchhoff rod theory, a special case of Cosserat rod theory (see Antman (2005) for an in-depth treatment of both). Kirchhoff theory assumes inextensibility and neglects transverse shear strain, which are generally regarded as good assumptions for long thin rods like the tubes that make up our active cannula. We also neglect gravitational effects in this analysis, because they have little effect at the scales and stiffnesses involved in our work. This can be seen from standard cantilever beam theory, which predicts a tip deflection caused by gravity of only 60 µm for a single straight, horizontally cantilevered tube 100 mm long, with an outer diameter (OD) of 1.6 mm, an inner diameter (ID) of 1.3 mm, and a Young’s modulus of 50 GPa. Note that this is a highly conservative calculation because (1) the actual cannula will consist of several concentric tubes and thus have a higher bending stiffness, (2) it will not generally be straight, (3) it will not generally be horizontally cantilevered, and (4) the elastic modulus may actually be up to 75 GPa (the manufacturer, NDC, Inc., quotes a range of 41–75 GPa). Thus, while it will certainly be useful in future work to develop models that take into account external loading (e.g. to enable force control of cannulas interacting with tissue), it does not appear to be necessary to consider gravitational loading in free-space models such as we derive in this paper. Similarly, we neglect friction as has been done in all active cannula models to date. Qualitatively the authors have observed some frictional hysteresis in prototypes with tightly packed tubes, but do not observe any discernible hysteresis in the prototype described in the experimental section of this paper. It is likely that frictional effects will be complex functions of a number of parameters including curvature functions, arc lengths, tolerances between tubes, surface smoothness, lubrication, etc., and a detailed study of all such effects is left to future work. Quantitatively, the suitableness of all of the assumptions listed above can be tested by comparing model predictions with experimental tip positions. We provide such a comparison in the experimental section of this paper.

2.2. Parameterization of Curves and Notation

Suppose that each tube in isolation is described by an arc-length-parameterized space curve t_i (s) for s ∈ [0, 1], with t_i (0) = 0. Let us attach a reference frame at each value of arc length, s, with the local z-axis pointing along the tangent to the curve, ṫ_i = dt_i/ds, and with the origin of the reference frame at t_i (s). Furthermore, let us establish the local x and y axes in any canonical way. For example, we can use the Frenet–Serret apparatus, or use Bishop’s frames (Bishop 1975), etc., as reviewed by Chirikjian and Kyatkin (2001). In any case, this will mean that a set of reference frames g_i (s) ∈ SE(3) will be defined, one for each tube as

$$g_i(s)=\left[\begin{array}{cc}\hfill R_i(s)\hfill & \hfill {\mathbf{t}}_i(s)\hfill \\ \hfill {\mathbf{0}}^{\mathrm{T}}\hfill & \hfill 1\hfill \end{array}\right],$$ (1)

where R_i (s) ∈ SO(3) is the rotation of the frame at the point s along the curve relative to the base frame at s = 0 and

$${\mathbf{t}}_i(s)={\int }_0^s{R}_i(\sigma ){\mathit{e}}_{3}d\sigma$$ (2)

is the translation of the frame.

Let us assume that the only degrees of freedom required to describe the conformations of each tube under all possible deformations due to moderate forces are bending and twisting. In other words, if $R_i^{*}(s)$ defines the precurved shape then the only admissible deformations will be of the form $R_i^{*}(s)\to R_i(s)\in \mathrm{S}\mathrm{O}(3)$. In this model, arc length is not changed by deformation (implying that each cannula tube behaves as an inextensible rod), and the relationship between position and orientation in (2) applies to the deformed parameters t_i (s), R_i (s) as well as the original parameters ${\mathbf{t}}_i^{*}(s),R_i^{*}(s),$ (implying that there is no shear strain in the deformations).

In general, R(s)^T Ṙ(s) ∈ 𝔰𝔬(3) is a 3 × 3 skew symmetric matrix, that can be parameterized by a three-vector. The isomorphism ℝ³ ≃ 𝔰𝔬(3) is defined by

$$^:\left[\begin{array}{c}\hfill {\omega }_1\hfill \\ \hfill {\omega }_2\hfill \\ \hfill {\omega }_3\hfill \end{array}\right]\mapsto \left[\begin{array}{ccc}\hfill 0\hfill & \hfill -{\omega }_3\hfill & \hfill {\omega }_2\hfill \\ \hfill {\omega }_3\hfill & \hfill 0\hfill & \hfill -{\omega }_1\hfill \\ \hfill -{\omega }_2\hfill & \hfill {\omega }_1\hfill & \hfill 0\hfill \end{array}\right],$$ (3)

where 𝔰𝔬(3) is the Lie algebra of SO(3). For Ω = ω̂ ∈ 𝔰𝔬(3), the inverse is given by ^∨ : Ω ↦ [ω₁ ω₂ ω₃]^T. The unit vectors e₁, e₂, e₃ ∈ ℝ³ are the standard basis.

2.3. The Kinetic Analogy

Throughout this paper we employ the well-known kinetic analogy from the mechanics literature, which enables one to discuss concepts from mechanics using language that is perhaps more familiar in the robotics community. For a review of the kinetic analogy see Kehrbaum and Maddocks (1997). In the context of this paper, use of the kinetic analogy has implications for interpretation of ω(s), which denotes a vector of arc-length-parametrized curvatures. For example, using any frame convention with its z-axis tangent to the curve (which we do exclusively in this paper¹), ω(s) is a vector of three elements, the first two of which denote curvatures about the x- and y-axes, and the last of which denotes the torsion about the z-axis. Equivalently, from the perspective of the kinetic analogy, ω(s) can be viewed as the angular velocity (parametrized by arc length rather than time) of a coordinate frame that travels along the centerline curve of the cannula. This distinction has no bearing on the mathematical equations presented in the remainder of this paper—the equations can be understood equally well from both perspectives.

2.4. Elastic Energy Stored in a Collection of Tubes

The deformation energy for an inextensible and shearless linearly elastic rod is given by

$$E=\frac{1}{2}{\int }_0^L{[\mathit{\omega }(s)-{\mathit{\omega }}^{*}(s)]}^{\mathrm{T}}K(s)[\mathit{\omega }(s)-{\mathit{\omega }}^{*}(s)]ds,$$ (4)

where ω*(s) = (R*(s)^T Ṙ*(s))^∨ is the local curvature (in the kinematic analogy the body “angular velocity” of the preshaped, unloaded tube frame g(s), with arc length as the independent variable rather than time) and ω(s) = (R(s)^T Ṙ (s))^∨ is the local curvature after deformation. Equation (4) is an expression for the strain energy due to bending and torsion in a rod under the assumption of the Bernoulli–Euler constitutive law in which the internal moment is proportional to the change in curvature. It is also invariant to frame assignment, meaning that use of Frenet–Serret frames, Bishop’s frames, or another frame convention will yield the same total energy. A very similar formulation of elastic energy in a Kirchhoff rod can be found in Bergou et al. (2008), and a more general formulation (for a tendon-driven continuum robot) which includes extensibility and shear is available in Gravagne (2002). In general, the symmetric stiffness matrix in (4) depends on the material properties of the tube, its geometry, and the way in which the reference frame is attached. For example, if the local x- and y-axes of the reference frame are attached according to the Frenet–Serret apparatus, and in this system K(s) is diagonal (and possibly also independent of s), then in another reference system, such as a Bishop’s frame which evolves along the backbone with minimal total orientational change, then K̃(s) = Q^T (s)K(s)Q(s) where Q(s) = exp {ê₃θ(s)} ∈ SO(3) is the relative rotation between these two systems of backbone reference frames around the z-axis. However, in the special case that

$$K=\left[\begin{array}{ccc}\hfill k_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill k_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill k_3\hfill \end{array}\right]$$ (5)

is constant in one such coordinate system (i.e. when the tube has an annular cross section), then K̃(s) = K. Thus, the stiffness matrix will be independent of the local orientation about the z-axis of the coordinate systems, and thus the energy will be also. For a cylindrical tube of constant cross-sectional inertia, I, and polar moment, J, then k₁ = EI and k₃ = GJ, where E denotes the Young’s modulus and G denotes the sheer modulus. Note that K can never be a scaled identity for cylindrical tubes, since

$$EI=GJ\Rightarrow \frac{E}{G}=\frac{J}{I}=2\Rightarrow 2(1+\nu )=2\Rightarrow \nu =0,$$

and, for physical materials, ν ≠ 0.

For a general n-tube cannula, we assume that all tubes overlap continuously for s ∈ [0, L]. Then, the stored elastic energy in entire device will be the sum of the energies stored in the individual tubes:

$$E=\frac{1}{2}\sum _{i=1}^n{\int }_0^L{[{\mathit{\omega }}_i(s)-{\mathit{\omega }}_i^{*}(s)]}^{\mathrm{T}}{K}_i(s)[{\mathit{\omega }}_i(s)-{\mathit{\omega }}_i^{*}(s)]ds,$$ (6)

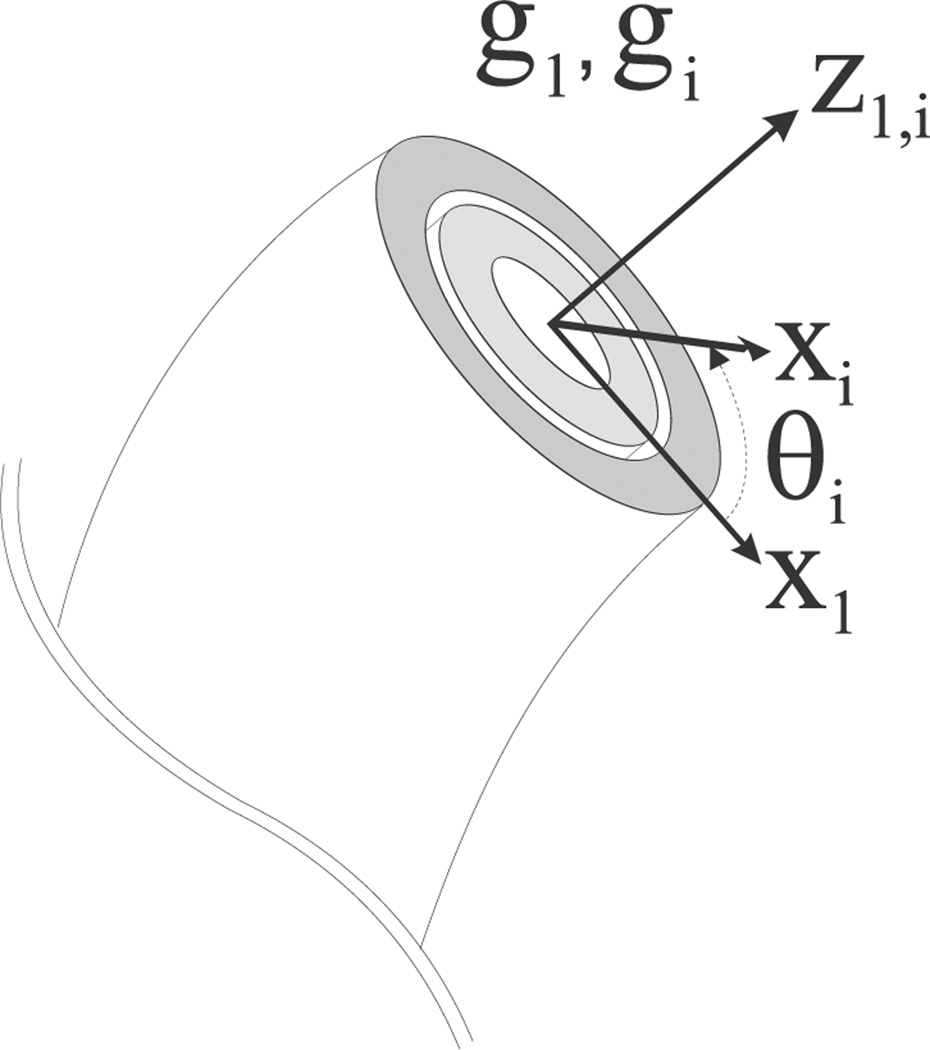
where ${\mathit{\omega }}_i^{*}(s)={(R_i^{*}{(s)}^{\mathrm{T}}{Ṙ}_i^{*}(s))}^{\vee }$ is the preshaped curvature and ω_i (s) = (R_i (s)^T Ṙ_i (s))^∨ is the equilibrium curvature for tubes i = 1, …, n. The tubes are concentric (and, thus, constrained to follow a common trajectory in space), implying t_i (s) = t₁(s). Hence, there are only 2 + n independent degrees of freedom to account for in the final deformed cannula. Specifically, suppose that the first tube is deformed via $R_1^{*}(s)\to R_1(s)$ (or, equivalently, ${\mathit{\omega }}_1^{*}(s)\to {\mathit{\omega }}_1(s)$, since $R_i^{*}(0)=R_i(0)=I$). This requires three degrees of freedom since ω₁ ∈ ℝ³. As can be seen from (2), all subsequent tubes must share the same z-axis, namely R_i (s)e₃ = R₁ (s)e₃, to ensure that t_i (s) = t₁ (s) for i = 2, …, n. This leaves only one extra degree of freedom per tube: a rotation around the z-axis. Thus, the final conformation of each tube can be parameterized with a rotation θ_i ∈ 𝕊¹ = ℝ mod 2π, namely R_i (s) = R₁ (s) exp {ê₃ θ_i (s)}, s ∈ [0, L], i = 2, …, n. Figure 2 illustrates how θ_i (s) relates g₁ (s) to g_i (s).

Fig. 2.

The coordinate frames for the first and the ith tubes at an arbitrary cross section of the active cannula. They differ by an angular rotation of θ about their z-axes, which are both tangent to the curve. The curvatures, ω and ω_i, of the frames are not pictured, since they may in general lie in any direction with respect to the coordinate frames.

The curvatures of coordinate frames along these subsequent tubes will be related to that of the first tube via

$${\mathit{\omega }}_i(s)=e^{-{\mathit{ê}}_3{\theta }_i(s)}{\mathit{\omega }}_1(s)+{\mathrm{\theta ̇}}_i(s){\mathit{e}}_3,i=2,\dots ,n.$$ (7)

Note that the energy functional (6) is invariant under actions of SO(3): the rotation R₁ does not appear in the expression. The objective of this paper is to minimize (6) over all paths

$$({\mathit{\omega }}_1(s),{\theta }_2(s),{\mathrm{\theta ̇}}_2(s),\dots ,{\theta }_n(s),{\mathrm{\theta ̇}}_n(s))\in {ℝ}^3\times T{𝕋}^{n-1}$$ (8)

on the interval s ∈ [0, L], where 𝕋^k = 𝕊¹ × ⋯ × 𝕊¹ (k times) denotes a k-torus, and T𝕋^k ≃ 𝕋^k × ℝ^k denotes its tangent bundle. Here, ℝ³ is identified with the tangent space of SO(3) via left translation, i.e. TSO(3) ∋ (R, Ṙ) ↦ (R, R^T Ṙ) ↦ (R, ω) ∈ SO(3) × ℝ³.

3. Two Special Cases

We now examine two special cases of the minimization of (6) using a variational approach, and show that for these cases, the variational approach reduces to “pointwise” minimization of the integrand in (6). We begin with a simple illustrative example of two tubes with co-planar precurvature. The result is the same as that obtained for circular curves in Webster et al. (2009), but here we generalize to variable planar curvature. We then consider the case where the two planar curves are rotated axially with respect to one another, but are infinitely torsionally rigid. Again, the result presented here for general curvatures agrees with previous results for piecewise constant curvatures, assuming no torsion (Sears and Dupont 2006; Webster et al. 2006b, 2009). It is also possible to include torsion in the straight transmission alone for piecewise constant curvature (Webster et al. 2009) in a straightforward manner. Therefore, we generalize in Section 4 and present the solution to the case in which any number of arbitrarily preshaped tubes are rotated axially at their bases with respect to one another, and undergo torsional deformation along the length of the curves. Unlike the special cases discussed in this section, solution to the general case requires a variational approach.

3.1. Planar Theory: A Degenerate Case

In the planar case, we can assume without loss of generality that all curvatures are of the form ω(s) = κ(s)_e1 where κ(s) is the curvature. The energy in this case will be

$$E=\frac{1}{2}{\int }_0^L\{k_1{(\kappa (s)-{\kappa }_1^{*}(s))}^2+k_2{(\kappa (s)-{\kappa }_2^{*}(s))}^2\}ds,$$ (9)

where k_i = E_i I_i. If we minimize this integrand pointwise with respect to κ(s), the result is

$$\kappa (s)=\frac{k_1{\kappa }_1^{*}(s)+k_2{\kappa }_2^{*}(s)}{k_1+k_2}.$$ (10)

This result is true independent of whether or not the stiffnesses depend on s, and it is also true independent of whether planar tube precurvatures are circular.

Note also that the same result can be obtained via variational methods. To see how this is true, simply replace κ with the equivalent θ̇, where θ is the counterclockwise-measured angle that the tangent to a curve makes with respect to a fixed line, and apply the Euler–Lagrange equation. In this case, the Euler–Lagrange equation reduces to ∂f/∂θ̇ = c where c is an arbitrary constant. This gives a result identical to (10) up to the constant of integration c. One can then determine c by substituting the result back into the original energy functional and noting that if there are no constraints on θ̇, then E is minimized when c = 0. Thus, the pointwise and variational minimization approaches produce the same result.

3.2. The Three-dimensional Case with No Torsion

Next, consider an active cannula with two tubes that are infinitely torsionally rigid. That is, tube cross sections are not able to rotate relative to one another about their common z-axes along their lengths, namely θ₂ = 0. This was the assumption in Webster et al. (2009) and Sears and Dupont (2006) for sections of the active cannula in which ${\mathit{\omega }}_1^{*}(s)\ne 0$ for any of the overlapping tubes. With a proper choice of coordinate frames, this reduces the variables over which we are minimizing (8) to ω = ω₁ = ω₂.

We seek the rotation matrix R(s) (or, equivalently, the curvature ω = (R^T Ṙ)^∨ since R(0) = I is known), and from this the corresponding curve defined by (2), such that the following energy is minimized:

$$E=\frac{1}{2}\sum _{i=1}^2{\int }_0^L{[\mathit{\omega }(s)-{\mathit{\omega }}_i^{*}(s)]}^{\mathrm{T}}{K}_i[\mathit{\omega }(s)-{\mathit{\omega }}_i^{*}(s)]ds.$$ (11)

Completing the square inside the integrand, we have

$$E=\frac{1}{2}{\int }_0^L{(\mathit{\omega }(s)-\mathit{\alpha }(s))}^{\mathrm{T}}K(\mathit{\omega }(s)-\mathit{\alpha }(s))+C(s)ds=\frac{1}{2}{\int }_0^L{(\mathit{\omega }(s)-\mathit{\alpha }(s))}^{\mathrm{T}}K(\mathit{\omega }(s)-\mathit{\alpha }(s))ds+\text{constant},$$

where

$$K=K_1+K_2,\mathit{\alpha }(s)=K^{-1}(K_1^{*}{\mathit{\omega }}_1(s)+K_2{\mathit{\omega }}_2^{*}(s)),\text{and}C(s)={\mathit{\omega }}_1^{*T}{K}_1{\mathit{\omega }}_1^{*}+{\mathit{\omega }}_2^{*T}{K}_2{\mathit{\omega }}_2^{*}-{\mathit{\alpha }}^{\mathrm{T}}K\mathit{\alpha }.$$

Here, C(s) is independent of ω, and its definite integral is a strictly positive constant. This can be seen by noting that the integrand in (11) is always non-negative, so when ω = α, the only piece of the integrand remaining is C(s), which must be greater than or equal to zero. Thus, ω(s) = α(s) provides the global energy minimum by minimizing the integrand in a “pointwise” fashion. This is the curvature that minimizes the energy, and is identical to the solution determined in Webster et al. (2006b, 2009) and Sears and Dupont (2006) for piecewise constant curvature tubes. One could also employ a variational approach to derive the energy minimum, as we will in the general case of the next section, namely the Euler–Poincaré equations.

4. The Many-tube Case with Torsion

We now turn our attention to the general problem of an active cannula with any number of tubes that are flexible in both bending and torsion. Here torsional deformation is allowed in the curved sections, unlike in prior work.

The stored elastic energy is given by (6). By using (7), the variables over which we are minimizing reduce to the set given in (8). To simplify notation, let ω(s) = ω₁ (s) denote the deformed curvature of the first tube and let t(s) = t_i (s). Denoting R_θ = e^ê₃θ(s), then from (7) we have ${\mathit{\omega }}_i=R_{{\theta }_i}^{\mathrm{T}}\mathit{\omega }+{\mathrm{\theta ̇}}_i{\mathit{e}}_3$.

Substituting (7) into (6), we have

$$E=\frac{1}{2}{\int }_0^L{[\mathit{\omega }-{\mathit{\omega }}_1^{*}]}^{\mathrm{T}}{K}_1[\mathit{\omega }-{\mathit{\omega }}_1^{*}]+\sum _{i=2}^n{[R_{{\theta }_i}^{\mathrm{T}}\mathit{\omega }+{\mathrm{\theta ̇}}_i{\mathit{e}}_3-{\mathit{\omega }}_i^{*}]}^{\mathrm{T}}{K}_i[R_{{\theta }_i}^{\mathrm{T}}\mathit{\omega }+{\mathrm{\theta ̇}}_i{\mathit{e}}_3-{\mathit{\omega }}_i^{*}]ds=\frac{1}{2}{\int }_0^L{\mathit{\omega }}^{\mathrm{T}}{K}_1\mathit{\omega }-2{\mathit{\omega }}^{\mathrm{T}}{K}_1^{*}{\mathit{\omega }}_1+{\mathit{\omega }}_1^{*T}{K}_1^{*}{\mathit{\omega }}_1+\sum _{i=2}^n({\mathit{\omega }}^{\mathrm{T}}{K}_i\mathit{\omega }+2{\mathit{\omega }}^{\mathrm{T}}{K}_i{\mathrm{\theta ̇}}_i{\mathit{e}}_3-2{\mathit{\omega }}^{\mathrm{T}}{R}_{{\theta }_i}{K}_i{\mathit{\omega }}_i^{*}+{\mathit{\omega }}_i^{*T}{K}_i{\mathit{\omega }}_i^{*}-2{\mathit{\omega }}_i^{*T}{K}_i{\mathrm{\theta ̇}}_i{\mathit{e}}_3+{\mathrm{\theta ̇}}_i^2{\mathit{e}}_3^{\mathrm{T}}{K}_i{\mathit{e}}_3)ds.$$ (12)

Since we are concerned with the case of tubes with annular cross sections, K_i is diagonal with its first two elements equal, and so

$${\mathit{\omega }}^{\mathrm{T}}{R}_{{\theta }_i}{K}_i{R}_{{\theta }_i}^{\mathrm{T}}\mathit{\omega }={\mathit{\omega }}^{\mathrm{T}}{K}_i\mathit{\omega }\text{and}{\mathit{\omega }}^{\mathrm{T}}{R}_{{\theta }_i}{K}_i{\mathrm{\theta ̇}}_i{\mathit{e}}_3={\mathit{\omega }}^{\mathrm{T}}{K}_i{\mathrm{\theta ̇}}_i{\mathit{e}}_3.$$ (13)

To simplify the above expression, let

$${\mathit{\omega ̅}}_i^{*}=R_{{\theta }_i}{\mathit{\omega }}_i^{*}-{\mathrm{\theta ̇}}_i{\mathit{e}}_3,K=\sum _{i=1}^n{K}_i,\mathit{\alpha }=K^{-1}(K_1{\mathit{\omega }}_1^{*}+\sum _{i=2}^n{K}_i{\mathit{\omega ̅}}_i^{*}),C={\mathit{\omega }}_1^{*T}{K}_1{\mathit{\omega }}_1^{*}+\sum _{i=2}^n{\mathit{\omega ̅}}_i^{*T}{K}_i{\mathit{\omega ̅}}_i^{*}-{\mathit{\alpha }}^{\mathrm{T}}K\mathit{\alpha },$$ (14)

Here, C = C(θ₂, θ₃, …, θ_n, θ̇₂, θ̇₃, …, θ̇_n) is a leftover non-negative constant as before, but now it depends on the state variables, as does α = α(θ₂, θ₃, …, θ_n, θ̇₂, θ̇₃, …, θ̇_n). As with the no torsion case of Section 3.2, we can complete the square:

$$E=\frac{1}{2}{\int }_0^L{(\mathit{\omega }-\mathit{\alpha })}^{\mathrm{T}}K(\mathit{\omega }-\mathit{\alpha })+Cds.$$ (15)

In our approach, one applies the Euler–Poincaré equations on the integrand of (15) with respect to the Lie group SO(3) × 𝕋ⁿ. For a derivation and review of the Euler–Poincaré equations see Kim and Chirikjian (2006) and Chirikjian (2011). This gives a system of differential equations in the variables ω, θ, θ̇:

$$K(\mathit{\omega ̇}-\mathit{\alpha ̇})+\mathit{\omega }\times (K(\mathit{\omega }-\mathit{\alpha }))=0$$ (16)

$$\frac{\partial f}{\partial {\theta }_i}-\frac{d}{ds}\left(\frac{\partial f}{\partial {\mathrm{\theta ̇}}_i}\right)=0.$$ (17)

For illustrative purposes, we note that (15) can be minimized pointwise by setting ω = α; this happens to be the trivial solution to (16).

Also, the application of static equilibrium conditions gives the same result (Rucker and Webster 2008). Writing a moment balance at an arbitrary cross section of the cannula and applying (7) and the definition of α, we have

$$K_1(\mathit{\omega }-{\mathit{\omega }}_1^{*})+\sum _{i=2}^n{R}_{{\theta }_i}{K}_i({\mathit{\omega }}_i-{\mathit{\omega }}_i^{*})=0\Rightarrow \mathit{\omega }=\mathit{\alpha }.$$ (18)

The algebraic relation ω = α provides ω in terms of θ₂, θ₃, …, θ_n and θ̇₂, θ̇₃, …, θ̇_n, so we apply (17) (which is also the classical Euler–Lagrange equation), to the functional in (15) n − 1 times, once with respect to each θ_i.

Below, we apply Euler–Lagrange before substituting in the relationship ω = α. Substituting before applying Euler–Lagrange is equivalent to assuming that ω = α is a holonomic constraint (Murray et al. 1994). This constraint turns out to be holonomic, which is verified by the fact that our result in the next section can be obtained by substituting before or after applying Euler–Lagrange. To apply the Euler–Lagrange equation to our functional f, we begin by first expanding f to obtain

$$f={\mathit{\omega }}^{\mathrm{T}}K\mathit{\omega }-2{\mathit{\omega }}^{\mathrm{T}}K\mathit{\alpha }+{\mathit{\omega }}_1^{*T}{K}_1{\mathit{\omega }}_1^{*}+\sum _{i=1}^n{\mathit{\omega ̅}}_i^{*T}{K}_i{\mathit{\omega ̅}}_i^{*}.$$ (19)

Based on this, the terms we need for the Euler–Lagrange equation are

$$\frac{\partial f}{\partial {\theta }_i}=-2{\mathit{\omega }}^{\mathrm{T}}K\frac{\partial \mathit{\alpha }}{\partial {\theta }_i}+2{\mathit{\omega ̅}}_i^{*T}{K}_i\frac{\partial {\mathit{\omega ̅}}_i^{*}}{\partial {\theta }_i},\text{and}\frac{\partial f}{\partial {\mathrm{\theta ̇}}_i}=-2{\mathit{\omega }}^{\mathrm{T}}K\frac{\partial \mathit{\alpha }}{\partial {\mathrm{\theta ̇}}_i}+2{\mathit{\omega ̅}}_i^{*T}{K}_i\frac{\partial {\mathit{\omega ̅}}_i^{*}}{\partial {\mathrm{\theta ̇}}_i}.$$ (20)

Then, noting that

$$\frac{\partial \mathit{\alpha }}{\partial {\theta }_i}=K^{-1}{K}_i\frac{\partial {\mathit{\omega ̅}}_i}{\partial {\theta }_i},\frac{\partial \mathit{\alpha }}{\partial {\mathrm{\theta ̇}}_i}=K^{-1}{K}_i\frac{\partial {\mathit{\omega ̅}}_i}{\partial {\mathrm{\theta ̇}}_i},\text{and}\frac{d}{dt}\left(\frac{\partial {\mathit{\omega ̅}}_i}{\partial {\mathrm{\theta ̇}}_i}\right)=0,$$ (21)

we can simplify the Euler–Lagrange equation to

$${(\mathit{\omega }-{\mathit{\omega ̅}}_i^{*})}^{\mathrm{T}}{K}_i=\frac{\partial {\mathit{\omega ̅}}_i^{*}}{\partial {\theta }_i}-{(\mathit{\omega ̇}-{\dot{\overline{\mathit{\omega }}}}_i^{*})}^{\mathrm{T}}{K}_i\frac{\partial {\mathit{\omega ̅}}_i^{*}}{\partial {\mathrm{\theta ̇}}_i}=0$$ (22)

for i = 2, …, n. Then applying ω = α, we have a set of n − 1 differential equations describing θ₂, …, θ_n,

$${(\mathit{\alpha }-{\mathit{\omega ̅}}_i^{*})}^{\mathrm{T}}{K}_i\frac{\partial {\mathit{\omega ̅}}_i^{*}}{\partial {\theta }_i}-{(\mathit{\alpha ̇}-{\dot{\overline{\mathit{\omega }}}}_i^{*})}^{\mathrm{T}}{K}_i\frac{\partial {\mathit{\omega ̅}}_i^{*}}{\partial {\mathrm{\theta ̇}}_i}=0,$$ (23)

where the boundary conditions are θ_i (0) = θ_i0 and θ̇_i (ℓ) = 0 for i ∈ {2, …, n}.

We note that using the Euler–Poincaré equations provided a simple one-step way to obtain the governing equations, whereas the method of a static equilibrium balance combined with the Euler–Lagrange equation provided the same result via a more circuitous route. This becomes important as the complexity of the model increases. Since the Euler–Poincaré equations are simpler to apply and require less physical intuition, they may be particularly advantageous in future work which may include, for example, the effects of shear and extension.

4.1. Model Evaluation

Numerical evaluation of active cannula models has been addressed previously by Rucker and Webster (2009a) and Rucker and Webster (2009b). For completeness, we provide a brief review of these results here. In general, one can solve this system numerically for θ₂, …, θ_n. The expression (23) can be expanded in terms of precurvatures and stiffness matrices as follows,

$${\mathit{e}}_3^{\mathrm{T}}(\sum _{j=2}^n{\mathrm{\theta ̈}}_j{K}_j{K}^{-1}-{\mathrm{\theta ̈}}_i)K_i{\mathit{e}}_3={\mathit{\alpha }}^{\mathrm{T}}{K}_i\frac{\partial R_{{\theta }_i}}{\partial {\theta }_i}{\mathit{\omega }}_i^{*}.$$ (24)

In the case of n = 2 and constant curvature $({\mathbf{\omega }}_i^{*}={\kappa }_{xi}{\mathit{e}}_1)$ this expression reduces to the differential equation derived in Rucker and Webster (2008). Equation (24) can be reformulated into a format amenable to numerical integration by first writing it in matrix form as

$$\mathit{\theta ̈}={\mathit{T}}^{-1}\mathit{f}({\theta }_2,\dots ,{\theta }_n),$$ (25)

where T = [t_i,j] is an n − 1 × n − 1 symmetric torsional stiffness matrix given by

$$t_{i,j}=\{\begin{array}{cc}\frac{-J_{i+1}{G}_{i+1}{\sum }_{k=1,k\ne i+1}^n{J}_k{G}_k}{{\sum }_{k=1}^n{J}_k{G}_k}\hfill & i=j,\hfill \\ \frac{J_{i+1}{G}_{i+1}{J}_{j+1}{G}_{j+1}}{{\sum }_{k=1}^n{J}_k{G}_k}\hfill & i\ne j.\hfill \end{array}$$ (26)

Here,

$$\mathit{\theta ̈}={\left[\begin{array}{ccc}\hfill {\mathrm{\theta ̈}}_2\hfill & \hfill \dots \hfill & \hfill {\mathrm{\theta ̈}}_n\hfill \end{array}\right]}^{\mathrm{T}},\text{and}\mathit{f}({\theta }_2,\dots ,{\theta }_n)={\left[\begin{array}{ccc}\hfill f_1\hfill & \hfill \dots \hfill & \hfill f_{n-1}\hfill \end{array}\right]}^{\mathrm{T}},$$ (27)

where

$$f_i={\mathit{\alpha }}^{\mathrm{T}}{K}_i\frac{\partial R_{{\theta }_i}}{\partial {\theta }_i}{\mathit{\omega }}_i^{*}.$$ (28)

One can use the standard state definition procedure to write (25) in the form of a first-order system ẋ = f(x) by augmenting the vectors on each side of the equation. Let x_i = θ_i+1 for 1 ≤ i ≤ n − 1 and let x_i = θ̇_i−n+2 for n ≤ i ≤ 2n − 2. The augmented first-order system is then

$$\mathit{ẋ}=\left[\frac{{[x_n,x_{n+1},\dots ,x_{2n-2}]}^{\mathrm{T}}}{{\mathit{T}}^{-1}\mathit{f}(x_1,x_2,\dots ,x_{n-1})}\right].$$ (29)

This system may now be solved with any of a number of numerical techniques for solving boundary value problems with mixed boundary conditions, for example Matlab’s bvp4c function, or a shooting method which iteratively converges on the proper initial conditions to satisfy the boundary conditions. Since all of the tubes are the same length here, the boundary conditions will be x_i (0) = θ_i+1 (0) for 1 ≤ i ≤ n − 1 and x_i (ℓ) = θ̇_i−n+2 (ℓ) = 0 for n ≤ i ≤ 2n − 2.

Equation (29) governs the behavior of a single section of overlapping tubes. It is straightforward to apply this to an active cannula with multiple regions of overlap, where tubes end at different arc lengths. One can consider each unique region of tube overlap (between arc lengths where tubes end) separately. In each region, the variables obey (29) for the particular combination of tubes in that section. All that must be done to join these separate systems together is to enforce continuity of the boundary conditions at the junctions between systems and shift each distal end boundary condition to the end of its particular tube. This procedure is mathematically equivalent to defining a new system similar to (29), but which is piecewise defined by a separate system for each unique region of tube overlap. However, this piecewise-defined differential equation will be discontinuous at points where curved sections begin and where tubes end. So, an adaptive step size numerical solver may unnecessarily attempt to refine the mesh around these points when integrating through them. Thus, for reasons of numerical efficiency and repeatable accuracy, we recommend the process of integrating each continuous section one at a time in series while algebraically enforcing continuity across the boundary from one section to the next.

Once one has solved (29) numerically to obtain all θ_i (s) and θ̇_i (s), the result can be used to obtain ω algebraically from (18). The resulting backbone trajectory of the cannula can be calculated by integrating Ṙ(s) = R^T (s)ω̂(s) to get R(s) and then integrating (2) to obtain t(s). There exist a number of numerical integration methods that preserve the structure of SE(3), which can be used to obtain R(s) from ω(s). For a review of these techniques we refer the reader to Park and Chung (2005).

In the remainder of this paper, we provide an analytical solution for an important special case of (23), where the active cannula consists of two circularly precurved tubes. A version of this analytical solution was first presented in Rucker and Webster (2008), and subsequently discussed further in Dupont et al. (2009). This special case is interesting because an analytical solution exists, and because despite the fact that many-tube active cannula prototypes have been built, all experimental inquiries to date into active cannula behavior have addressed exclusively this particular case (see e.g. Webster et al. (2009) and Dupont et al. (2009). Our general model (23) and more specifically the analytical solution of the special case, provides the first means for exploring the effects of torsion on active cannula shape.

4.2. Analytical Solution for Two Circular Tubes with Torsion

While (23) can be solved numerically for any number of component tubes, much insight into the fundamental behavior of active cannulas can be gained buy considering the case of an active cannula composed of two circularly precurved tubes, for which an analytical solution can be found. Without loss of generality, one can define the two tube frames such that ${\mathit{\omega }}_1^{*}={[{\kappa }_1\mathrm{0\; 0}]}^{\mathrm{T}}$ and ${\mathit{\omega }}_2^{*}={[{\kappa }_2\mathrm{0\; 0}]}^{\mathrm{T}}$. Expanding (23) in this case yields

$$\frac{G_1{J}_1{G}_2{J}_2}{G_1{J}_1+G_2{J}_2}\mathrm{\theta ̈}-{\kappa }_1{\kappa }_2\frac{E_1{I}_1{E}_2{I}_2}{E_1{I}_1+E_2{I}_2}\text{sin}\theta =0,$$ (30)

where θ₂ has been replaced with θ. Under the assumption that the two tubes have the same value of ν, Poisson’s ratio, this equation reduces to

$$\mathrm{\theta ̈}-{\kappa }_1{\kappa }_2(1+\nu )\text{sin}\theta =0,$$ (31)

however, we will not make this assumption here, for the sake of generality. Let

$$a={\kappa }_1{\kappa }_2\frac{E_1{I}_1{E}_2{I}_2(G_1{J}_1+G_2{J}_2)}{G_1{J}_1{G}_2{J}_2(E_1{I}_1+E_2{I}_2)},$$ (32)

so that

$$\mathrm{\theta ̈}-a\text{sin}\theta =0.$$ (33)

The appropriate boundary conditions here are the initial angle determined by the relative angular position of the tube bases, θ(0) = θ₀, and the natural boundary condition at the free end, θ̇(L) = 0. This natural boundary condition can be intuitively understood by considering that θ̇(s) ∝ axial torque applied at s. At L there is no torque being applied to the distal end of either tube. Thus, θ̇(L) = 0.

Note that (33) has the same form as the differential equation which describes a simple pendulum. Fortunately, this equation arises often, and it has a known analytical solution in terms of Jacobi’s elliptic functions. We solve it following the solution procedure similar to the method described in Ames (1968), which begins by multiplying both sides of (33) by θ̇, and integrating once. Applying the boundary condition θ̇_L = 0 then yields

$${\mathrm{\theta ̇}}^2+2a\text{cos}\theta =2a\text{cos}{\theta }_L.$$ (34)

Rearranging (34), we obtain

$$s=\pm \frac{1}{\sqrt{2a}}{\int }_{{\theta }_0}^{\theta (s)}\frac{d\theta }{\sqrt{\text{cos}{\theta }_L-\text{cos}\theta }}.$$ (35)

Now we use cos(θ + π(1 + 2n)) = − cosθ for all n ∈ Z, and cos 2θ = 1 − 2 sin² θ, to write this in terms of incomplete elliptic integrals of the first kind as follows. First let

$$\gamma =\theta +\pi (1+2n),k=\text{sin}\frac{{\gamma }_L}{2}=\sqrt{\frac{1-\text{cos}{\gamma }_L}{2}},$$ (36)

and let Φ be defined by

$$\text{cos}\gamma =1-2k^2{\text{sin}}^2\mathrm{\Phi }.$$ (37)

Then we have

$$\text{cos}\gamma -\text{cos}{\gamma }_L=2k^2{\text{cos}}^2\mathrm{\Phi }\text{and sin}\gamma =2k\text{sin}\mathrm{\Phi }{(1-k^2{\text{sin}}^2\mathrm{\Phi })}^{1/2}.$$ (38)

So that (35) becomes

$$s=\pm \sqrt{\frac{1}{a}}{\int }_{\mathrm{\Phi }(0)}^{\mathrm{\Phi }(s)}\frac{d\mathrm{\Phi }}{\sqrt{1-k^2{\text{sin}}^2(\mathrm{\Phi })}}=\pm \sqrt{\frac{1}{a}}(F(\mathrm{\Phi }(s),k)-F(\mathrm{\Phi }(0),k)),$$ (39)

where F(Φ, k) is the elliptic integral of the first kind with amplitude Φ and modulus k. We can now use the Jacobi amplitude functions, sn and cn which are the sine and cosine of the inverse function of F defined by the identities

$$\mathrm{s}\mathrm{n}(F(\mathrm{\Phi },k),k)=\text{sin}\mathrm{\Phi }\text{and}\mathrm{c}\mathrm{n}(F(\mathrm{\Phi },k),k)=\text{cos}\mathrm{\Phi }$$ (40)

to obtain the following solutions:

$$\theta (s)=2{\text{sin}}^{-1}(k\mathrm{s}\mathrm{n}(F(\mathrm{\Phi }(0),k)\pm \sqrt{a}s,k))-\pi (1+2n)\mathrm{\theta ̇}(s)=\pm 2k\sqrt{a}\mathrm{c}\mathrm{n}(F(\mathrm{\Phi }(0),k)\pm \sqrt{a}s,k).$$ (41)

The ± signs in (41) and take the same sign as θ_L − θ₀, and n is chosen such that γ_L takes on a value in the range −π ≤ γ_L ≤ π.

4.3. Examples

In order to illustrate how to use the solution described above to obtain the shape of an active cannula, and to investigate the phenomena of multiple solutions and non-circular equilibrium shapes, we provide the following example. Consider a tube and a wire with properties given in Table 1. The long curved lengths of L₁ = 200 mm and L₂ = 140 mm for the inner wire and the outer tube, respectively, make the interaction of the curved portions pronounced and thus more easily visualizable. The boundary condition at the proximal end, where s = 0, is θ(0) = θ₀ = α₂ − α₁, where α₂ and α₁ are the base rotation angles applied by the actuators at the tube bases. The boundary condition at the free distal end where the outer tube ends (s = L₂) is θ̇_L2 = 0, which was already implicitly enforced on our solution in Equation (34). The analytical solution (41) contains the unknown constant, θ_L2 within k, so we need to find a solution for θ_L2 which satisfies the proximal boundary condition θ₀ = α₂ − α₁. We can then think of “starting at the distal end” and use the change of variables σ = L₂ − s to rewrite (41) in terms of θ_L2 as

$$\theta (\sigma )=2{\text{sin}}^{-1}(k\mathrm{s}\mathrm{n}(F(\mathrm{\Phi }(L_2),k)\pm \sqrt{a}(\sigma ),k))-\pi (1+2n),$$ (42)

so that θ_L2 must be determined to satisfy

$${\alpha }_2-{\alpha }_1-2{\text{sin}}^{-1}(k\mathrm{s}\mathrm{n}(F(\mathrm{\Phi }(L_2),k)\pm \sqrt{a}(L_2),k))-\pi (1+2n)=0.$$ (43)

This can be done using standard non-linear root finding techniques such as MatLab’s fzero. Once θ_L is found, the analytical solution (41) is used to obtain θ(s), which enables us to obtain each tube’s deformed curvature from (18) and (7). Then, the resulting shape of each tube can be obtained by numerically integrating Ṙ_i (s) = R_i (s)e^ω̂(s)_i and using (2) to determine t(s).

Table 1.

Physical Properties of the Tube and Wire used in the Simulation

	Outer tube	Inner wire
Young’s modulus (GPa)	58	58
Shear modulus (GPa)	21.5	21.5
Inner diameter (mm)	2.01	0
Outer diameter (mm)	2.39	1.60
Length (mm)	140	200
Curvature (mm−1)	0.0099	0.0138

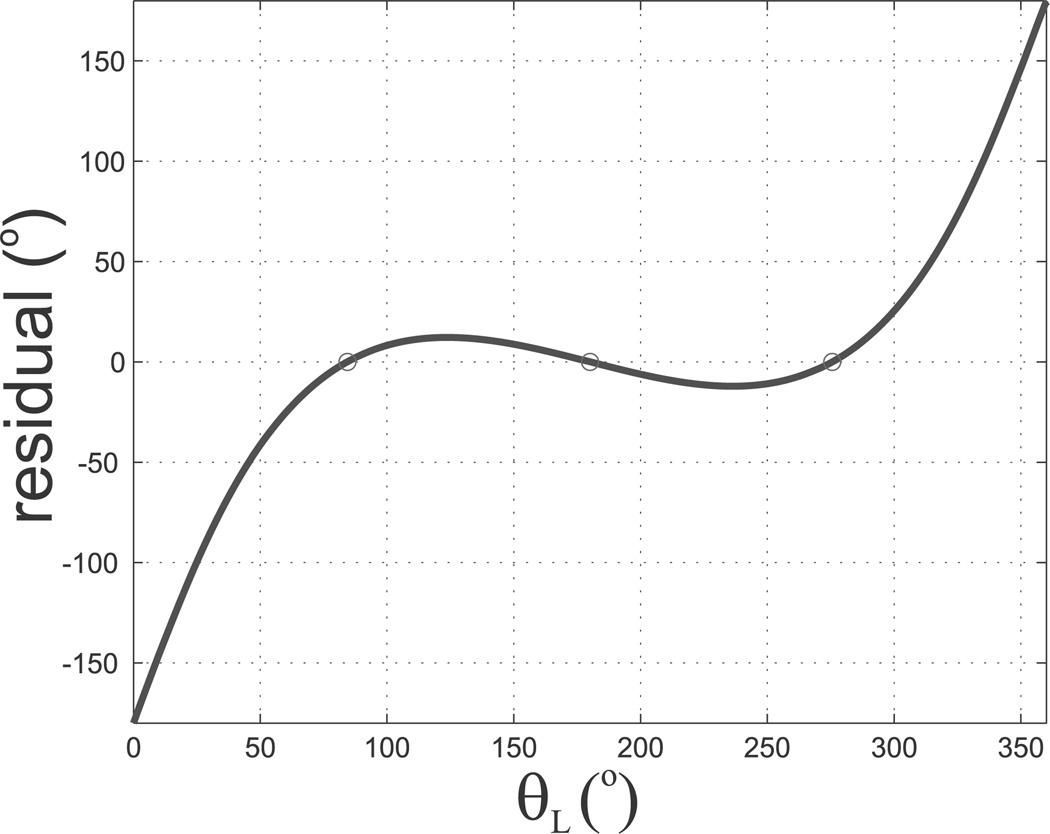
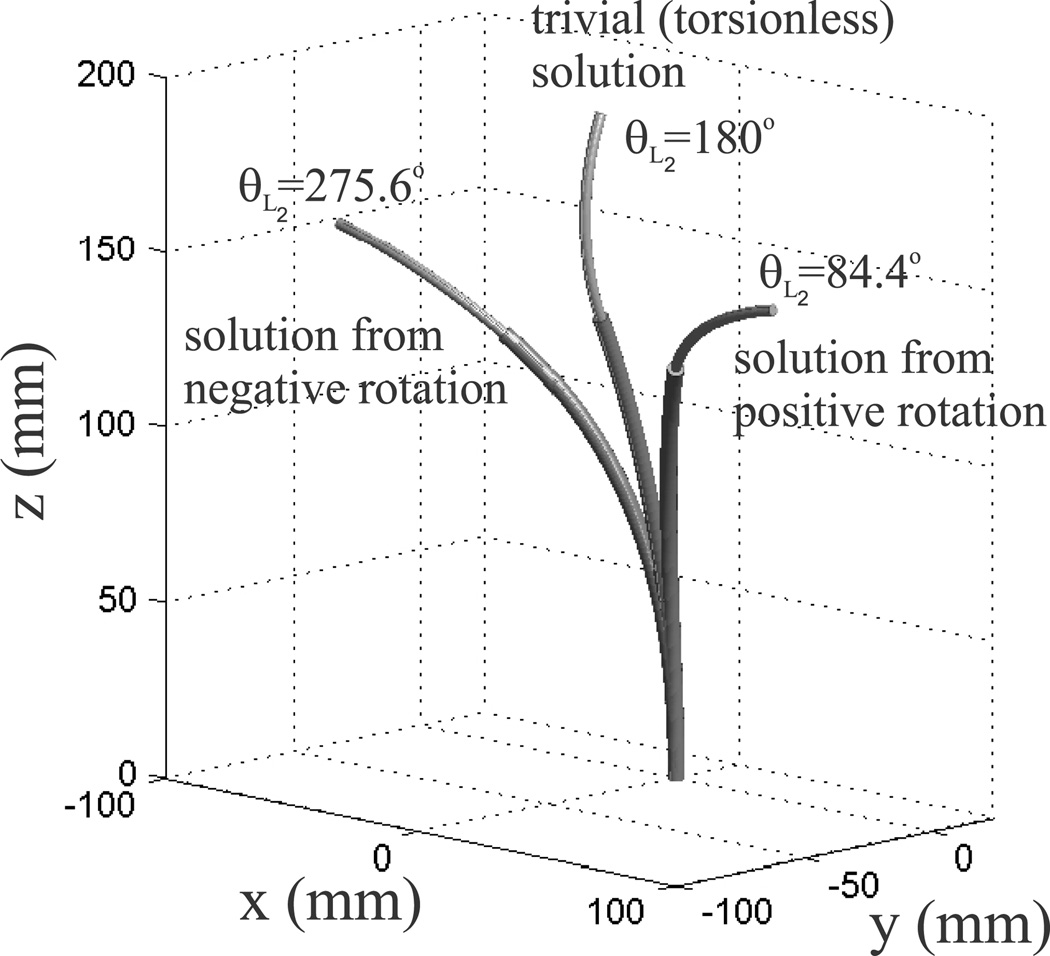
Webster et al. (2009) considered torsion in straight transmission sections of a cannula. It was shown that in this case, multiple solutions (local minimum energy configurations) can emerge. We see the same phenomenon here. In general, there can be more than one value of θ_L which satisfies (43). The particular root which the algorithm converges to is dependent on the initial guess. As noted by Webster et al. (2009) the particular configuration (solution) taken by the cannula will depend on actuator history. We illustrate this phenomenon in our example below. The inner wire is rotated to an angle of α₁ = −180°, while the outer tube stays at α₂ = 0°, making θ₀ = 180°. The left-hand side of Equation (43) is depicted in Figure 4 with respect to θ_L2. Note that there are three places where the graph crosses the x-axis, representing three different solutions to (43), and corresponding to the three different configurations shown in Figure 3. The solution at θ_L2 = 180° is a trivial solution to the differential equation, representing the case where neither tube undergoes any torsion (a torsionally rigid model would produce this result). This is an unstable configuration in that the cannula will snap to one of the other solutions if perturbed slightly. The cannula will reach the θ_L2 = 84.4° solution if the actuator starts at α₁ = 0° and increases α₁ continuously until α₁ = 180°. If the actuator decreases continuously from α₁ = 0° to α₁ = −180°, the solution θ_L2 = −84.4° will be reached, which corresponds to the α_L2 = 275.6° solution for α₁ = 180°. In order to solve (43) for the value of θ_L2 which corresponds to the actual configuration of the cannula, it is helpful to start simulating at a known configuration for which there is only one solution (e.g. θ₀ = 0). Then, by undergoing incremental changes in θ₀, the solution for θ_L at the previous step can be used as the initial guess for the current configuration. This results in the simulation portraying the same solution as the physical cannula until a bifurcation in the cannula energy is reached (where the current solution vanishes, see Webster et al. (2009)) and the cannula “snaps around” to a new solution.

Fig. 4.

Plot of the left-hand side of Equation (43) versus θ_L for the tubes in Table 1 and θ₀ = 180°. Solutions for θ_L satisfying (43) are shown at θ_L = 180°, θ_L = 84.4°, and θ_L = 275.6°.

Fig. 3.

Simulation of the tubes given in Table 1 with the inner wire rotated to a base angle of α₁ = −180° so that θ₀ = 180°. Three equilibrium conformations are shown corresponding to the three boundary condition solutions shown in Figure 4. The solution with θ_L2 = 84.4° is reached by rotating α₁ in the negative direction to α₁ = −180°, and the solution θ_L2 = 275.6° is be reached by rotating α₁ in the positive direction to α₁ = 180°. The solution with θ_L = 180° is the trivial (unstable) solution, with the tubes undergoing no torsion.

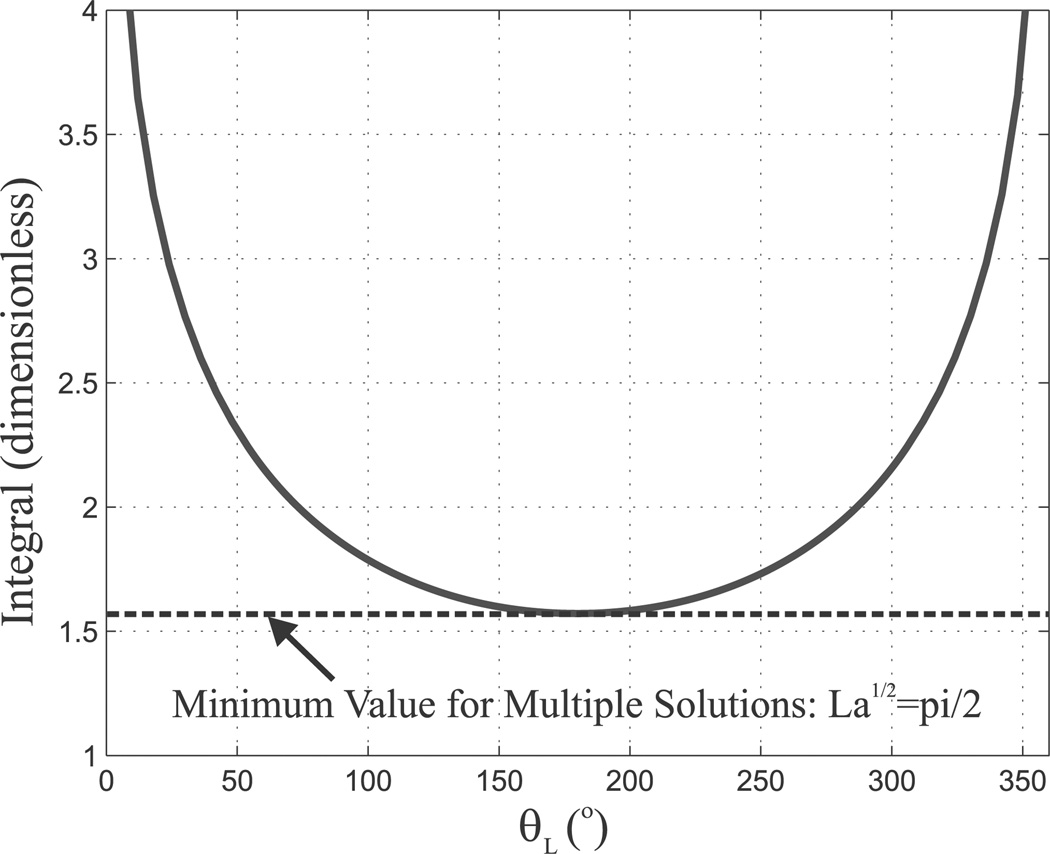
For the a simple, two-tube, circular precurvature case we are currently considering, it is possible to predict analytically when multiple solutions will exist (see Dupont et al. (2009) for an alternate derivation of the following result). For θ₀ = 180° (the angular input where multiple solutions will first exist) we can examine the integral in Equation (39) to determine whether multiple solutions are possible. If θ_L = 180°, the integral is zero by definition, which means cannulas of any overlapped length have a solution θ_L = 180°. For θ_L ≠ 180°, the integral has a lower bound of π/2, which can be seen in Figure 5 and is shown in (44). Thus, by rearranging (39) and applying this inequality, it can be seen that for cannulas with a value of $L\sqrt{a}<\pi /2$, only the trivial solution exists. On the other hand, if $L\sqrt{a}\ge \pi /2$, two non-trivial solutions also exist, symmetric about θ_L = 180°. Thus, as shown in (45), the dimensionless parameter $L\sqrt{a}$, which is composed of the overlapped length, stiffness, and curvature of the tubes, can be used to predict whether a two tube cannula will exhibit multiple solutions and thus have the potential to “snap” from one stable solution to another.

Fig. 5.

For θ₀ = 180° the value of the integral in (44) is shown in blue as a function of θ_L ranging from 0° to 360°. Because it is lower bounded by π/2, the dimensionless parameter $L\sqrt{a}$ can be used to predict when multiple solutions can occur.

To summarize our multiple solutions discussion above, we have the inequality

$$\pi /2\le \left|{\int }_0^{\mathrm{\Phi }(L)}\frac{d\mathrm{\Phi }}{\sqrt{1-k^2{\text{sin}}^2(\mathrm{\Phi })}}\right|\text{for all}{\theta }_L\ne 180°,$$ (44)

which when combined with (39) yields the conditions:

$$L\sqrt{a}<\pi /2\to \text{only one solution},L\sqrt{a}\ge \pi /2\to \text{multiple solutions exist}.$$ (45)

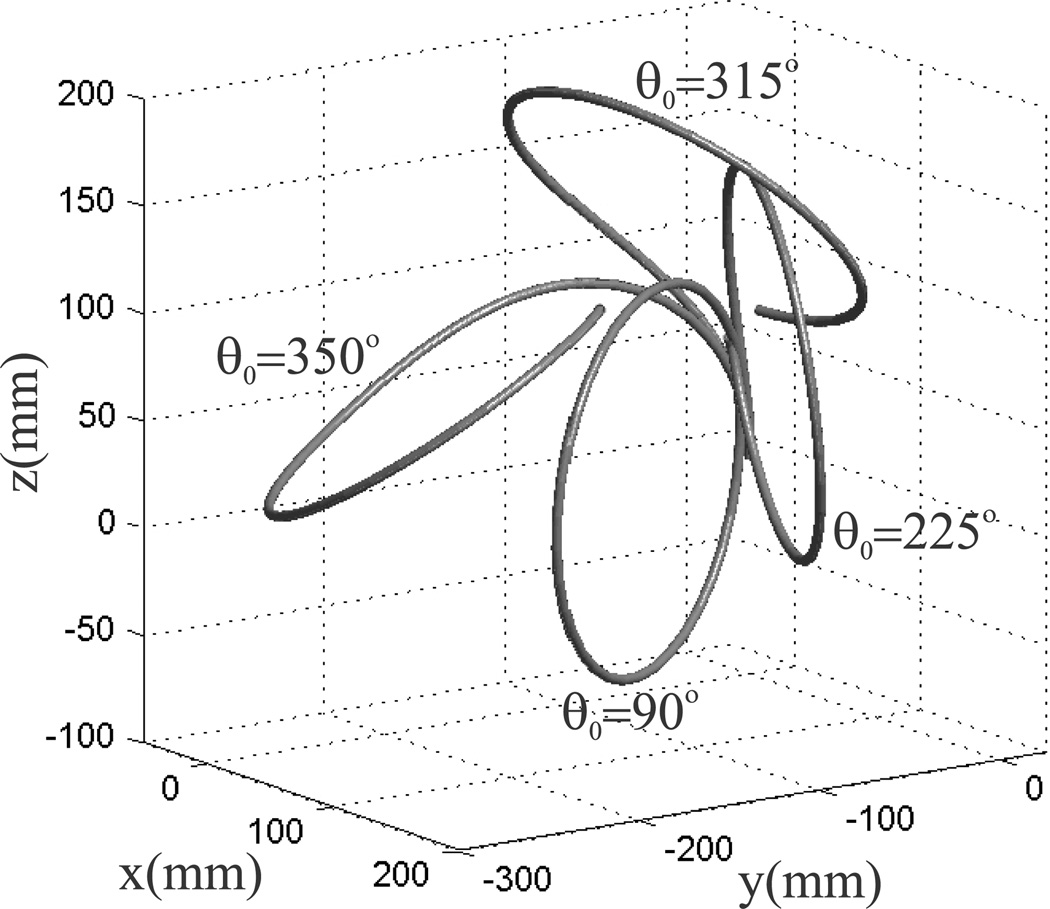
As shown in Figure 3, the two solutions with torsion are significantly different than the no torsion solution. Thus, torsion in the overlapping curved section can be very important for determining overall shape. Still, it would appear that each section is very close to circular, suggesting that some kind of adjustment to a piecewise circular model could be an effective way to compensate for torsion in the curved sections. Modeling the individual sections of an active cannula as circular arcs leads to very convenient kinematic formulations that have been widely exploited in prior work (e.g. Webster et al. (2009), Furusho et al. (2006), Sears and Dupont (2006), etc., see also Webster and Jones (2010) for an overview of piecewise constant curvature kinematics for continuum robots). However, the presence of torsion can, in some cases, lead to curved shapes that are qualitatively different and which cannot be approximated well by circular arcs. If the overlapped arc length is long or the curvatures are large, torsional relaxation makes it possible to obtain highly non-circular shapes from two circularly precurved tubes. To illustrate this, we extend the curved portions of both tubes used in our first example to 636.5 mm (corresponding to one full circle of the outer tube) and rotate the inner wire from α₁ = 0° to α₁ = 350°. The resulting shape is shown in Figure 6, where the inner wire has been rotated in the positive direction to angles of 90°, 225°, 315°, and 350° at the base. It is clear from Figure 6 that the resulting shape cannot be well approximated by a circle. However, for cannulas of sufficiently short curved overlap and sufficiently small curvature, piecewise circular models are reasonably accurate at predicting cannula shape. Such was the case for many prior prototypes (e.g. Webster et al. (2009) and Sears and Dupont (2006)).

Fig. 6.

Four configurations of a simulation of two fully precurved, fully overlapping tubes, whose material properties are given in Table 1. Both tubes have a longer arc length of 636.5 mm (equal to one full circle of the outer tube). The inner wire is rotated in the positive direction to angles of 90°, 225°, 315°, and 350° at the base. It is evident that in extreme cases, circular tubes with precurvature can form highly non-circular shapes when combined due to the effects of torsion.

5. Experimental Validation of the Analytical Model

The range of possible diameters for active cannula robots is defined by the diameters of elastic tubes that can be manufactured, shaped, and actuated. The prototype used in this study is composed of superelastic Nitinol tubes, but any material with a high recoverable strain that can be appropriately shaped (e.g. plastics) may be used. Nitinol tubes can be shape-set by heat treatment or plastic deformation, and are available in stock sizes ranging from 0.2 to 8.0 mm (see www.nitinol.com). Furthermore, the dexterity of the design improves with miniaturization because smaller tubes can sustain higher precurvatures (Webster et al. 2006b).

In this section we compare the predictions of three available models for active cannula shape with a set of experiments on a prototype cannula. The three models are the “bending only” model (Sears and Dupont 2006), the “transmissional torsion” model (Webster et al. 2006b, 2008, 2009), and the model provided in Section 4, a preliminary version of which was presented in Rucker and Webster (2009a). The experimental data set used here is the same as that provided in Webster et al. (2009).

5.1. Model Implementation

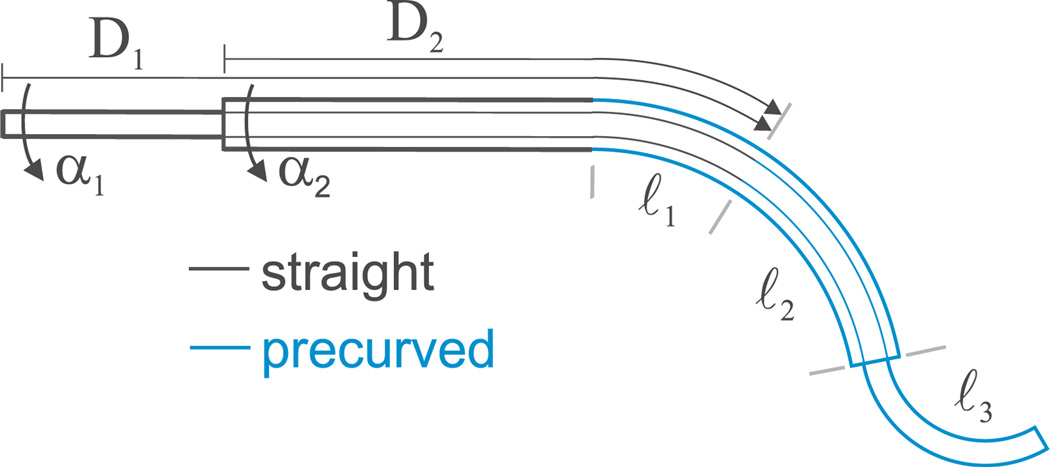
As described in Webster et al. (2009), these experiments use an active cannula constructed of one tube and one wire, each of which has an initial straight transmission, followed by a circularly curved section near its tip. Thus, as shown in Figure 7, this prototype can be considered to have four distinct regions or “links”, which begin and end where tubes begin and end, or where tubes transition from straight to curved. For example, beginning at the base of the cannula, the links will often be as follows: (1) a link where both tubes are straight, (2) a link where one tube is curved and the other is straight, (3) a link where both tubes are curved, and (4) a link where only one tube is present and curved.

Fig. 7.

Diagram of tube overlap configuration with variables from (46) shown.

Since our experimental prototype contains straight transmission segments that connect the actuators to the start of the curved tube sections, our model implementation must account for the torsional compliance of the transmission in addition to that of the curved sections. In order to use the general model directly as derived in Section 2, we (without loss of generality) consider s = 0 to refer to the point where both tubes become curved (the beginning of link 2, labeled ℓ₂, in Figure 7). We need to modify the boundary condition given by (43) to account for the straight length of each tube before it becomes curved. We know that the angle of twist for both tubes varies linearly with arc length in the sections which have at least one straight tube (the trivial solution of (6) with n = 2). Using this and the fact that the moments about the z-axes to achieve α₁ and α₂ must balance, we can obtain

$${\mathrm{\theta ̇}}_0-({\theta }_0-{\alpha }_1+{\alpha }_2)\frac{G_1{J}_1+G_2{J}_2}{G_1{J}_1{D}_2+G_2{J}_2{D}_1}=0,$$ (46)

thus (46) is to be satisfied instead of (43) where θ₀ and θ̇₀ are expressed as functions of the unknown value θ_L2 as follows

$${\theta }_0({\theta }_{L_2})=2{\text{sin}}^{-1}(k\mathrm{s}\mathrm{n}(F(\mathrm{\Phi }(L_2),k)\pm \sqrt{a}(L_2),k))-\pi (1+2n){\mathrm{\theta ̇}}_0({\theta }_L)=\pm 2k\sqrt{a}\mathrm{c}\mathrm{n}(F(\mathrm{\Phi }(L_2),k)\pm \sqrt{a}(L_2),k),$$ (47)

where D₁ and D₂ are the arc lengths between the actuators and the link in which both tubes are curved, and α₁ and α₂ are the tube base input angles as shown in Figure 7.

5.2. Experimental Dataset

Here, we summarize the experimental data set (the dataset from Webster et al. (2009)) which was used to compare the model given in Section 2 with the transmissional torsion model. In these experiments, an outer tube and an inner wire were arranged in two different translational positions and a range of input angles were applied. The two translational positions were referred to as the “full overlap case” and the “partial overlap case”. In the full overlap case, the tube and wire were arranged so that the link lengths were as follows: ℓ₁ = 10 mm (tube curved, wire straight), ℓ₂ = 82.3 mm (both curved), and ℓ₃ = 2.7 mm (only wire present). For the full overlap case, data was recorded for 15 different input angles ranging from 0° to 280° in 20° increments. In the partial overlap case, the tube and wire were arranged so that the link lengths were as follows: ℓ₁ = 48 mm, ℓ₂ = 44.3 mm, and ℓ₃ = 40.7 mm. For this overlap configuration, data was recorded for 11 different input angles ranging from 0° to 200° in 20° increments. The workspace range covered by these actuation inputs is depicted in Figure 9.

Fig. 9.

Configuration space covered in experiments. Left: partial overlap case. Right: full overlap case.

5.3. Procedure and Model Calibration

Each of the above configurations were input to the base of the cannula tube and wire using the manual actuation unit shown in Figure 8. For each, the resultant overall shape of the cannula was recorded via a calibrated pair of stereo cameras (Sony XCD-X710 firewire cameras with a resolution of 1,024 × 768 pixels). The fiducial markers shown in the inset image in Figure 8 enabled determination of point correspondences for stereo triangulation, after they had been identified in image coordinates by manually clicking on the center of the black bands in video frames. One source of error in this data collection procedure is the accuracy of manual point selection in images, which is estimated to be approximately 2 pixels or 0.6 mm. Another is fiducial size (they are not infinitesimal points), causing small differences in intended selection locations. We estimate that fiducial dimensions introduce error of approximately the diameter of the wire itself (1.6 mm). Based on these, our overall vision system measurement error is approximately 2.2 mm, in a worst-case sense.

Fig. 8.

Manual actuation mechanism used in the experiments. In this apparatus, both tube and wire are affixed to circular acrylic input handles at their bases, which are etched to encode rotation. The support structure is etched with a linear ruler to encode translation. Spring pin locking mechanisms lock the input disks at desired linear and angular input positions. The inset image of a striped cannula on a white background is an example of an image captured using one of our calibrated stereo cameras. The black bands seen are electrical tape and allow for point correspondences to be identified for stereo triangulation. The red circles indicate the locations at which Euclidean errors were calculated. Calibration of model parameters was done to minimize the sum of these errors over all experiments.

The nominal physical properties of the tube and wire used in our experiments are given in Table 2.We compare the model of Section 4 with the prior transmissional torsion model using both the nominal values given in Table 2 and calibrated parameters (a calibration procedure for the transmissional torsion model is provided in Webster et al. (2009)). Examining the equations in Section 4, we see that the stiffness coefficients in Equations (18) and (33) can be expressed in terms of the three dimensionless parameters

$$c_1={\nu }_1,c_2={\nu }_2,\text{and}{c}_3=\frac{E_1{I}_1}{E_1{I}_1+E_2{I}_2}.$$ (48)

Table 2.

Measured and Assumed Physical Quantities for the Experimental Tube and Wire

	Outer tube	Inner wire
Young’s modulus (GPa)	58	58
Shear modulus (GPa)	21.5	21.5
Inner diameter (mm)	2.01	0
Outer diameter (mm)	2.39	1.60
Straight length (mm)	93.5	218.5
Curved length (mm)	92.3	85
Curvature (mm−1)	0.0099	0.0138

Poisson’s ratio is often taken to be approximately 0.35 for Nitinol. It has also been noted that plastic deformation can increase Poisson’s ratio for Nitinol to 0.5 (White 2001). Since we preshaped our tubes via plastic deformation, we assume a range of 0.30–0.50. An expected range for c₃ can be deduced from the uncertainty in each quantity upon which it depends. Nitinol dimensions are specified by the manufacturer (Nitinol Devices and Components, Inc.) to ±0.0010 inch, while the elastic modulus E is reported as 41–75 GPa. Applying standard error propagation, the expected range for parameter c₃ is 0.143–0.431. These ranges provide a basis for comparison with fitted parameter values produced by the parameter fitting procedure. To calibrate the parameters, we minimize the sum of the positional errors at the tip of the wire, the tip of the tube, and the measured point nearest the base, as shown in Figure 8. Matlab’s fmincon function was used to optimize the values of the three dimensionless parameters given in (48) with upper and lower bounds set to the expected ranges of the parameters. As described in Webster et al. (2009), the transformation between the stereo camera coordinate frame and a frame fixed at the base of the cannula was first estimated using point cloud registration (Arun et al. 1987). Images of a 15-mm checkerboard pattern (with corners at known physical locations with respect to the cannula base frame) were captured. Sixteen corners on the checkerboard were triangulated with the stereo vision system. This registration was only expected to provide a rough estimate of the frame transformation. Thus, six “nuisance parameters” (a three-vector for position and a three-vector for orientation with magnitude of rotation encoded as length) describing the cannula base frame were included in the calibration procedure and initialized with the results from the point cloud registration. Nuisance parameters showed only small changes during optimization, with cannula base frame moving only 0.5 mm, and rotating through X–Y–Z Euler Angles of α = 0.9°, β = 0.3°, and γ = 4.0°.

5.4. Results

The calibrated parameter values are given alongside their nominal values in Table 3, and we note that they fall well within their expected ranges and converge to near the same values for initial guesses in a range within ±5% of the optimal values. In Webster et al. (2009), calibration led to one of the parameters falling outside its expected range, which illustrates that the model presented in this paper captures the underlying mechanics more completely. Note that the unmodeled presence of friction would have a similar effect on our data as lowering the torsional rigidity of the tubes, namely increasing torsional windup. Thus, the calibration process would tend to increase c₁ and c₂ to compensate for frictional effects. This may account for the slightly high values of c₁ and c₂, but they are nevertheless still within their expected ranges.

Table 3.

Nominal and Calibrated Dimensionless Parameters

Parameter	Nominal value	Calibrated value
c1	0.350	0.451
c2	0.350	0.449
c3	0.287	0.341

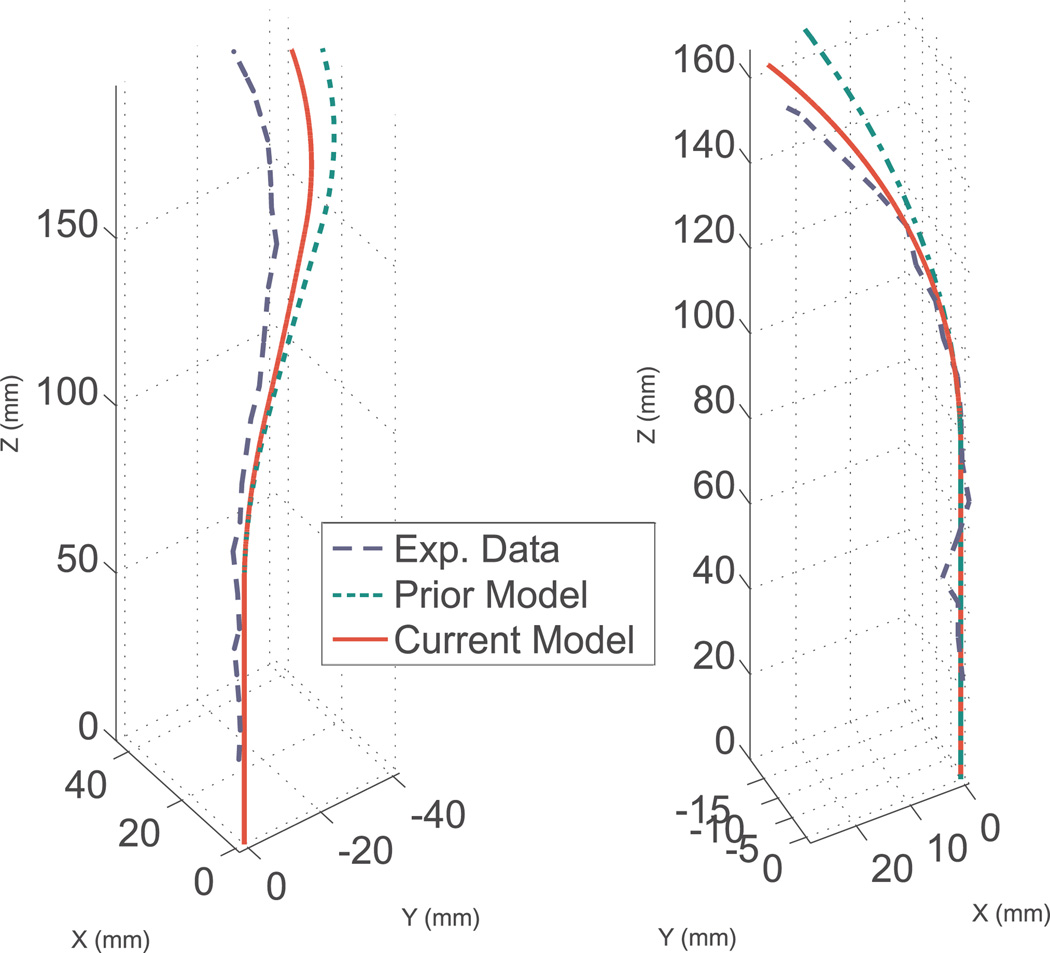
This is also supported by the data in Table 4. When using nominal parameters from data sheets, the model of Section 4 is significantly more accurate than the transmissional torsion model. Specifically, the model of Section 4 results in an average tip error of only 4.72 mm as opposed to 10.1 mm for the transmissional model. Figure 10 shows the experimental data and the predictions of both models using nominal parameters for the two worst experimental cases, where angular input angle differences are at the edge of the workspace and torsion is most significant. These are 280° in the full overlap case, and 200° in the partial overlap case.

Table 4.

Uncalibrated Tip Error Statistics for the Current Model Compared with Prior Models

	Mean tip error (mm)	Maximum tip error (mm)
Bending only model	24.8	54.3
Transmissional torsion model	10.1	22.1
Model of Section 4	4.7	12.7

Fig. 10.

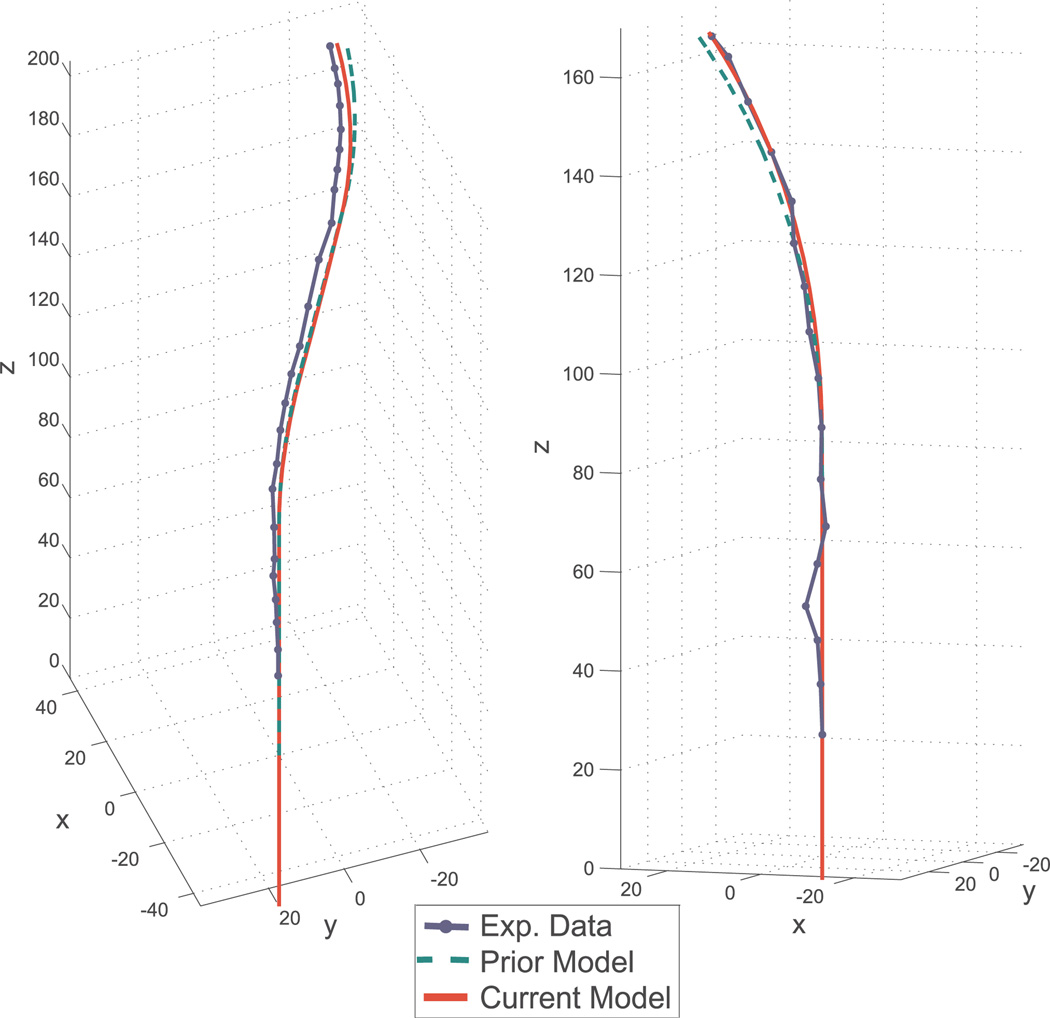
Comparison of shape for the transmissional torsion model (green – dotted line) with nominal parameters, the model given in Section 4 (red – solid line) with nominal parameters, and experimental data (blue – dashed line) for configurations near the edge of the active cannula workspace. Note that the model given in Section 4 produces predictions closer to experimentally observed cannula shape. Left: partial overlap case. Right: full overlap case.

Quantitatively, the model of Section 4 with calibrated parameters exhibits a mean tip error of 2.5 mm across all experiments with a maximum tip error of 7.1 mm, as shown in Table 5). In comparison, the calibrated transmissional torsion model exhibits a mean of 3.0 mm and a maximum of 8.8 mm, and the bending only model a mean of 13.6 mm and a maximum of 31.5 mm. With calibrated parameters, the model of Section 4 improves the mean tip error 82% over the bending only model, and 17% over the transmissional torsion model.

Table 5.

Calibrated Tip Error Statistics for the Current Model Compared with Prior Models

	Mean tip error (mm)	Maximum tip error (mm)
Bending only model	13.6	31.5
Transmissional torsion model	3.0	8.8
Model of Section 4	2.5	7.1

Plots of the experimental data and the predictions of both models using calibrated parameters are shown in Figure 11, picturing the same two “worst-case” experiments shown in Figure 10. The behavior pictured is common to all experimental positions using either calibrated or uncalibrated parameters, namely that the prediction of the model of Section 4 lies nearer the experimental data than the transmissional torsion model prediction. Note also that the predictions of the bending only model are not shown for clarity, since they are sufficiently far from the experimental data that they would obscure the differences between the other two models. As discussed by Webster et al. (2009), the bending only model neglects the torsional windup that occurs in an active cannula, so its predictions become increasingly structurally incorrect as the angle input difference increases.

Fig. 11.

Comparison of shape for the transmissional torsion model (green – dotted line) with calibrated parameters, the model given in Section 4 (red – solid line) with calibrated parameters, and experimental data (blue – dashed line) for configurations near the edge of the active cannula workspace. Note that the model given in Section 4 produces predictions closer to experimentally observed cannula shape. Left: partial overlap case. Right: full overlap case.

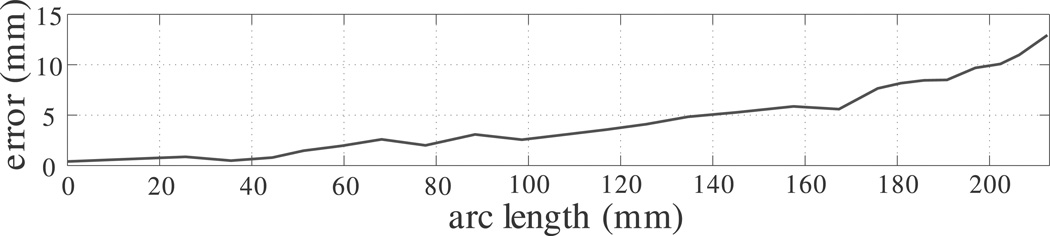
To demonstrate the fact that tip error is a good metric to use, we give the error between the model prediction with nominal parameters and the experimental backbone location in Figure 12 as a function of arc length for the worst experimental case (the left-hand case in Figure 11). It shows the common characteristic that the positional error increases with arc length.

Fig. 12.

Error versus arc length for the 200° partial overlap case with nominal parameter values using the model of Section 4. The general increase in error from base to tip is characteristic of all experiments, and thus tip error provides a reasonable metric for our experimental dataset.

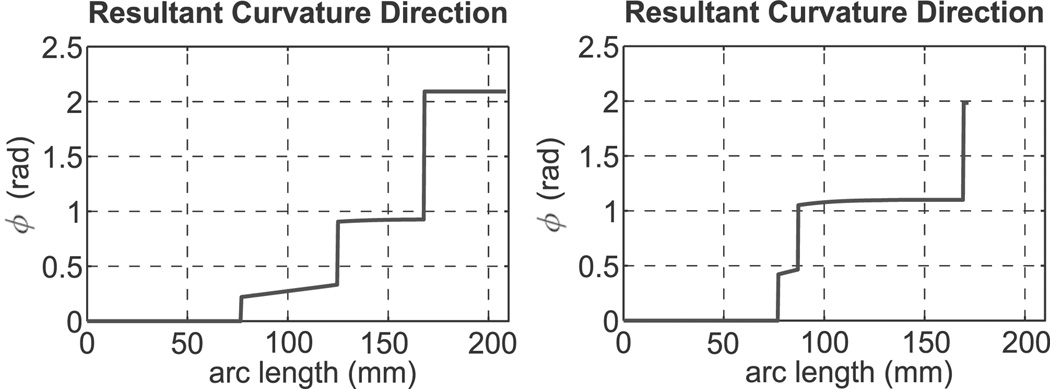
Using the model of Section 4, Figure 13 shows the angle defining the plane of curvature of the experimental cannula as a function of arc length. The plot shows that while this angle is not exactly piecewise constant, it is approximately so. This illustrates why previous studies (e.g. Webster et al. (2006b) and Sears and Dupont (2006)) have successfully used models which imply piecewise constant curvature. The out-of-plane motion was small enough that it was not obvious experimentally, and cannula shape was approximately piecewise circular. These quantitative results also indicate that the general modeling framework is providing enhanced predictive ability by reducing tip error, and thus may expand the range of medical procedures to which active cannulas can be applied.

Fig. 13.

Angle ϕ of that defines the resulting instantaneous plane of curvature of the active cannula. Left: partial overlap case. Right: full overlap case.

6. Conclusions

We have presented a general coordinate-free energy formulation for modeling the shape of concentric tube continuum robots known as active cannulas. This formulation is able to account for precurvatures and stiffnesses that vary along the length of component tubes, and to explicitly model torsion throughout the device. Further, previous models are special cases of this new general modeling framework, and we showed that the moment balance equations assumed in prior work arise naturally within our new modeling framework. In this work we also showed via simulation and experiments that the new model described in this paper captures the underlying mechanics of the cannula more accurately than prior models. This was illustrated in simulation by the fact that tubes with circular precurvatures can combine to form a dramatically different shape if torsion is allowed in curved sections. In the experiments it was shown that the calibrated parameter values fell within their expected ranges, which was not the case for the model with only transmissional torsion.

This new model may have significant implications for active cannula applications in both medicine and industry. In this paper we have not addressed design guidelines for active cannulas, a discussion of which can be found in Webster et al. (2009) and Webster (2007). Rather, we have provided the model necessary to simulate possible designs and judge their merits in comparison to design goals. Explicitly accounting for torsion throughout the cannula can significantly enhance the model, enabling active cannulas to be used in more demanding applications. Furthermore, active cannulas with variable precurvatures will be able to reach further and through more complex trajectories while using fewer tubes. This new model also facilitates future studies on patient-specific preshaping of active cannula component tubes, so that one may match the capabilities of the device to the particular location and entry trajectory required by a specific patient. An important area for future work is the development of active cannula models that consider external loading. This may be accomplished through use of the Euler–Poincaré approach, or by application of Cosserat rod theory. As suggested by Mahvash and Dupont (2008) and partially explored by Rucker et al. (2010), such a future model will be useful for determining cannula shape when it is interacting with tissue, using the cannula itself as a force sensor (by sensing shape), and implementing force controllers. If it becomes necessary in future models to take into account the effects of shear and elongation or other complicating factors, the Euler–Poincaré approach may be particularly valuable.