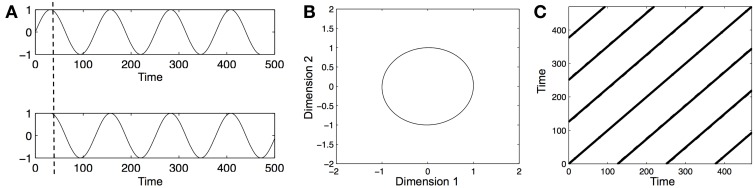
Figure 1.

Illustration of time series embedding, phase-space reconstruction, and recurrence plot analysis. (A) A sine wave over several periods (top panel) and a delayed copy of that time series. The original time series and its time-delayed copy are plotted against each other to yield a 2-dimensional phase-space. (B) Phase-space portrait of a sine-wave. The circular shape of the profile shows that the sine-wave is highly stable and repetitive, repeating itself perfectly along a single circular path. Please note that the labeling of the dimensions as 1 and 2 is arbitrary. (C) Recurrence plot (RP) of the phase-space portrait. In a RP, time at lag0 runs along the central diagonal. The presence of the diagonal line states the simple fact that a time series is always the same with itself at lag0. The striped pattern that repeats itself off the diagonal toward the upper left and the lower right indicates that the time series is perfectly repeating itself, and the distance between the stripes (i.e., the white spaces between them) indicates the lag at which the time series repeats itself, and is equal to the period of the sine-wave. Since all recurrent points fall onto diagonally adjacent lines, the %DET values = 99.9% (as the sine-wave is perfectly deterministic, the values should be 100%, but spurious individual recurrence points can appear on the edges of the RP, leading to the negligible deviation from the expected value).