Probing the Mechanical Properties of Magnetosome Chains in Living Magnetotactic Bacteria

Abstract

The mechanical properties of cytoskeletal networks are intimately involved in determining how forces and cellular processes are generated, directed, and transmitted in living cells. However, determining the mechanical properties of subcellular molecular complexes in vivo has proven to be difficult. Here, we combine in vivo measurements by optical microscopy, X-ray diffraction, and transmission electron microscopy with theoretical modeling to decipher the mechanical properties of the magnetosome chain system encountered in magnetotactic bacteria. We exploit the magnetic properties of the endogenous intracellular nanoparticles to apply a force on the filament-connector pair involved in the backbone formation and stabilization. We show that the magnetosome chain can be broken by the application of external field strength higher than 30 mT and suggest that this originates from the rupture of the magnetosome connector MamJ. In addition, we calculate that the biological determinants can withstand in vivo a force of 25 pN. This quantitative understanding provides insights for the design of functional materials such as actuators and sensors using cellular components.

The mechanical properties of cells are of primary importance for the understanding of force transduction, which in turn impacts physiological and pathological states.¹ Cytoskeletal proteins are typically involved in cellular substructures that are associated with the sensing and transmission of mechanical signals² with impact on cellular processes including cell shape, division, polarity, and motility.^3,4 Therefore, considerable efforts have been spent on characterizing the mechanical properties of cytoskeletal filaments. However, determining such properties for molecular complexes in vivo has proven to be difficult.

In vitro measurements are typically performed on purified cell components such as, e.g., cytoskeletal proteins by rheometry,⁵ atomic force microscopy,⁶ optical microscopy,⁷ or some combination of them.⁸ However, in vitro studies only give semiquantitative information about cytoskeletal filaments since the measurements involve interaction with extra-cellular objects⁷ or because the fabricated filaments lack the scaffolding complexity and might therefore not fully reflect the complexity observed in vivo.⁶ In vivo measurements rely on bead addition⁹ or use a spatially unresolved application of stress.¹⁰ In particular, magnetic beads were one of the first probes used for the in vivo determination of mechanical properties of macromolecular scaffolds.¹¹ Meanwhile, magnetic nanoparticles have emerged as promising tools to tune molecular responses such as, e.g., microtubule assembly¹² or cell death.¹³

However, synthetic nanoparticles can have detrimental effects on, e.g., intracellular tension and cellular migration.¹⁴ Thus, an unbiased characterization technique or a proper biological system for the probing of such molecular forces in vivo remains to be found. In the meantime, magnetotactic bacteria provide a unique opportunity for studying cell mechanics since they biomineralize endogenous magnetite nanoparticles called magnetosomes, which are organelles produced for the navigation in aquatic habitats along magnetic field lines.¹⁵ Magnetosomes comprise membrane-enveloped, nanosized crystals that are intracellularly organized in chains.¹⁶ The molecular players involved in the chain formation have been largely unraveled in the magnetospirilla,¹⁷⁻²³ for which genetic modifications are possible, and therefore have established as generic model systems in magnetotactic bacteria. MamK, a member of the actin family, forms the magnetosome filament to which magnetosome vesicles attach with the help of MamJ, the magnetosome connector. The alignment of bacteria in an external magnetic field is based on a mechanically stable MamJ/MamK interaction in order to effectively rotate the cells. If MamK is also present in other strains, this is not the case of MamJ.²⁴ Since no genetic systems are established for these strains, much less is known about the molecular players involved in biomineralization, but other proteins might play a similar role as it has, e.g., been shown that LimJ can play a redundant function to MamJ in Magnetospirillum magneticum AMB-1.²¹ Magnetic nanoparticles are thus naturally present within these microorganisms and are bound to a well characterized macromolecular scaffold. Therefore, the magnetospirillum system represents an ideal model for the testing of intracellular mechanical forces in vivo without the need of additional exogenous reporter particles. Moreover, with the recent success in expressing the magnetotactic genes in a foreign organism,²⁵ this approach to mechanical probing of the cells may become more widely applicable.

Here, we present a study of the mechanical properties of the magnetosomes particles attached to the magnetosome filament via the magnetosome connector. We make use of the magnetic properties of the magnetosomes to exert a force on the filament–connector couple by rotating an external magnetic field around mechanically fixed living bacteria. We use a combination of optical and electron microscopy, synchrotron-based X-ray diffraction (XRD) and theoretical calculations to show that the magnetosome chains are mechanically extremely stable since they remain unaffected by external magnetic field of strength lower than 30 mT, which is about 500 times the strength of the Earth magnetic field of 50 to 60 μT. We finally identify the magnetosome connector MamJ as the weakest part of the network and calculate that the proteineous material can withstand a force of 25 pN, a measure obtained in a living system.

Potential Effect of Magnetic Field Rotation around Magnetotactic Bacteria

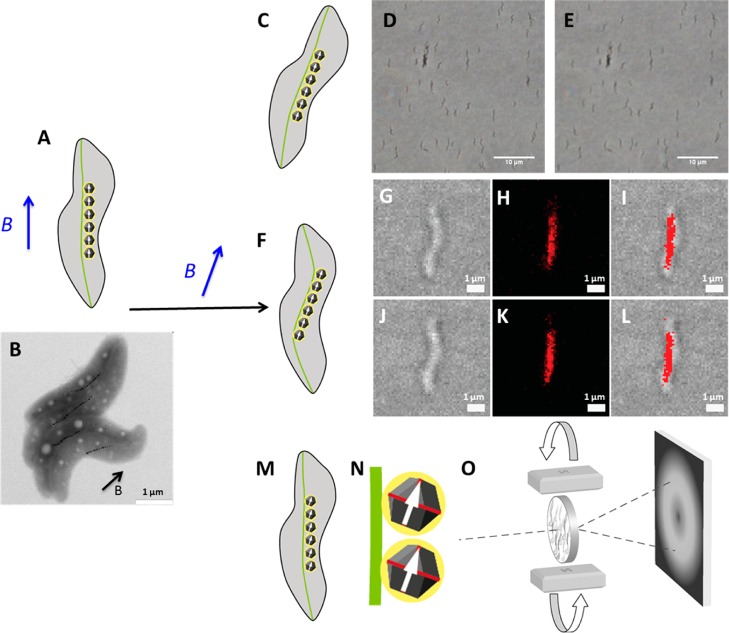
Magnetotactic bacteria passively align in external magnetic fields thanks to their magnetosome chain (Figure 1A,B). In this study, we aim at preventing this alignment to probe the inner substructures of the cell with forces arising from an external magnetic field. Therefore, a fixing method is required, rigid enough to hold the bacteria but soft and hydrating enough not to kill them. If so, rotation of a magnet around the cells exerts forces directly on intracellular substructures. It is, however, not clear at what level these forces affect the magnetosome chain. The magnetosome filament is either deformed so that the whole chain aligns with the field (Figure 1F) or the magnetosomes themselves are turned (Figure 1M,N). These different cases are studied and presented below.

Figure 1.

Possible effects of rotating a magnetic field B (in blue) around a magnetotactic bacterium. Cell, chain, and particle are initially aligned with the external field (A, scheme; B, transmission electron microscope (TEM) image of cells aligned on a grid). While the direction of the field is changed, the whole bacterium will rotate in the absence of any support (C). The bacteria are fixed if embedded in an agarose gel as shown by optical microscopy: bacteria in the presence of a magnetic field of 150 mT in different field directions (before and after rotation of the field by 90° in, respectively, D and E). The bacteria do not align with the external field in this case. Another possibility for fixed bacteria is that the magnetosome chain rotates as a single entity (F). Optical microscopic transmission (G,J), fluorescence (H,K), and overlay (I,L) images of fixed mCherry-MamK labeled cells before (G, H, and I) and after (J, K, and L) perturbation by changes in the field orientation show no evident displacement of the magnetosome filament. Finally, the individual magnetosome particles could turn (M, and larger view in N), which we studied by X-ray diffraction (O).

We used commercially available low melt agarose, which gels at 24–28 °C, to immobilize living bacteria.²⁶ Briefly, the bacteria are placed in an agarose solution cooled at 30 °C. By placing the suspension in a magnetic field of 150 mT, the bacteria aligned with the field. The fixation of the bacteria is obtained by cooling the sample to 4 °C. After such a treatment, the bacteria are no longer able to move when the external field orientation is changed (Figure 1D,E) but remain alive.

Magnetosome Filament Does Not Show High Flexibility

We then tested the properties of the magnetosome filament and thus performed the same experiment as above but using a genetically engineered strain (Figure 1F). mCherry-MamK exhibits fluorescence around the magnetosome filament as the related MamK-GFP strain.²⁷ If the magnetosome chain, which is usually depicted as a single magnetic dipole,^28,29 rotates as a whole, possibly with some deformation due to its confinements within the cell, the field rotation should be reported at the filament level. However, the fluorescent signal is independent of the magnetic field direction (Figure 1G–L). We note that small changes in the filament position cannot be detected due to the resolution limit of fluorescence microscopy of about 250 nm. Nevertheless, this observation indicates that the magnetosome filament, made of the actin-like protein MamK, is not easily deformed by the torque exerted on the magnetosomes by the external magnetic field.

Organized Magnetotactic Bacteria Display Textured XRD Pattern

The crystal orientation of magnetite particles inside dried bacteria can be followed by 2D XRD.³⁰ We proceed similarly with our immobilized cells. The living bacteria are mounted in a way that the direction of alignment is perpendicular to the beam (Figure 1N). The obtained 2D diffraction shows an amorphous halo, originating from the water in the agarose. Apart from this signal, several diffraction rings are detected. After azimuthal integration, the position of the rings (the peaks in the diffractogram I (Q)) can be assigned to magnetite³¹ (Figure S1B, Supporting Information). Furthermore, a fiber texture is observed, i.e., the intensity distribution along the Debye rings is nonuniform.³² The intensity variations of the Debye rings along the azimuth angle I(γ), evaluated by radial integration and local background subtraction of the 2D pattern (see methods), reveals a [111] fiber axis, meaning that the magnetite crystals have one of their [111] directions parallel to each other.

Magnetosome Crystals Rotate with Large External Magnetic Field Strength, Not with Small Ones

The magnetosome crystal orientation is that of the observed fiber axis. Thus, if the direction of the fiber axis ψ shifts within the plane perpendicular to the beam, a shift of the azimuthal intensity variation I(γ) is observed. By analyzing the shift of the I(γ + ψ), the direction of the fiber axis ψ can be measured and thereby the orientation of magnetite crystals (Figure S1C-E, Supporting Information).

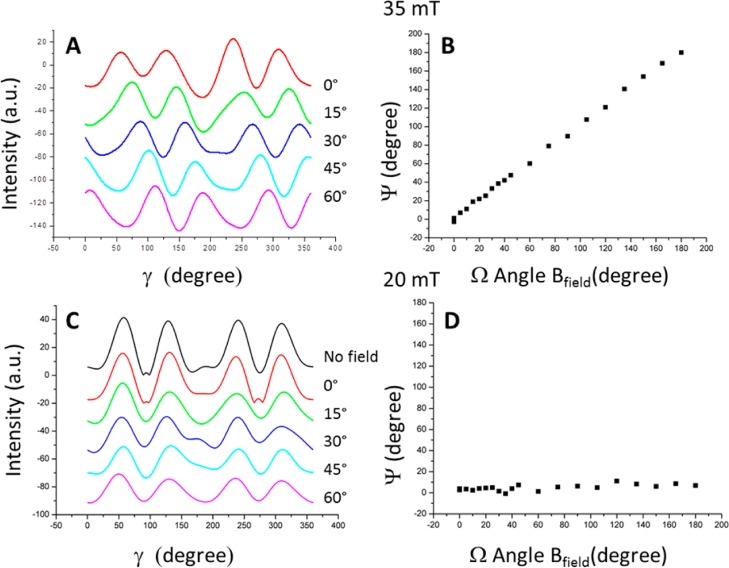
As described above, we observe a textured intensity profile for all XRD measurements. In the case of the rotation of a strong magnetic field with a strength of 35 mT or larger (Figure 2A,B), a change of the angle of the applied magnetic field (Ω) leads to a change of the texture in the 2D X-ray pattern. In particular, the profiles look similar for different field angles (Figure 2A), and the shifts are strongly correlated with the angle of the external field (Figure 2B). Plotting the angle of the fiber axis ψ against the angle of the magnetic field Ω indeed yields a linear dependence (slope 1.004 ± 0.007, R² = 0.992). This shows that the orientation of the crystals follow the direction of the magnetic field.

Figure 2.

Influence of external magnetic fields with different field strengths. In fields stronger than 30 mT (A,B), the crystals rotate with the applied field. Below 30 mT (C,D), the crystals are maintained in their original orientation. Ψ is the direction of the measured fiber axis, and Ω is the angle of the applied magnetic field.

Reducing the field strength to 30 mT or below, the effect of changing the external field direction is dramatically different (Figure 2C,D). The direction of the fiber axis ψ of the texture profile is no longer following the direction of the external field Ω. The direction of the majority of the crystals does not rotate with the field but stays at or close to its initial position of 0° (Figure 2D). Thus, for these field strengths, the crystals withstand the torque exerted by the external field and maintain their original orientation.

Magnetic Interparticle Interactions Alone Cannot Explain the Observed Pattern of Rotation

A theoretical framework is thus developed to understand the effect of the field strength on crystal orientation. We describe the magnetosome chain as N freely rotating interacting magnetic dipoles with fixed positions in space and consider the energy contributions of the magnetic interactions between magnetosomes (internal field) and of the external magnetic field exerted by the rotating magnets. The energy is written

1

For a chain of N magnetosomes with individual dipole moment of m, the interaction with the external field results in

2

The approximation originates from the assumption that all dipoles have the same magnetic moment m and the same angle α with respect to the chain axis (Figure S3, Supporting Information).

The internal field experienced by a given magnetosome within the chain is composed of the influence of the field of all the other magnetic dipoles of the chain. This energy contribution is calculated by the dipole–dipole interactions (see methods/Supporting Information). With the same approximation that all magnetosomes have the same angle with respect to the chain axis, it can be written as

3

Here B_int characterizes the field strength that one dipole experiences due to the presence of the other dipoles in the chain and depends on the geometric parameters (particle radius and separation) as well as on material parameters (see methods). The energetically most favorable state is obtained by minimizing the total energy with respect to α. In Figure 3A this angle is shown as a function of the angle of the external field Ω for 3 different field strengths (20, 35, and 150 mT). For the calculations, a chain of 20 crystals with a crystal radius of 20 nm and an interparticle distance of 10 nm is used, in agreement with literature values,¹⁵ leading to an internal field strength B_int ≈ 15 mT.

Figure 3.

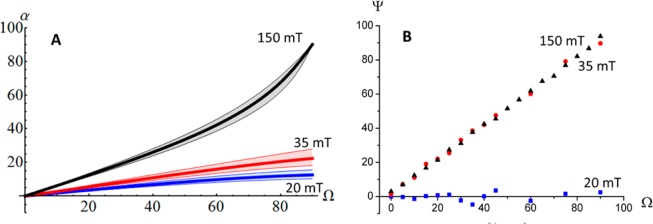
(A) Calculated orientation (angle α) of the dipole moments of crystals arranged in a chain dependent manner with an external field at an angle Ω. Different field strengths are shown (black, 150 mT; red, 35 mT; blue, 20 mT). The crystal radius is r = 20 nm, the interparticle distance d = 10 nm (d/2r = 0.25), and the number of crystals N = 20 for the thick lines. The light areas represent an error zone where the d/2r values are changed from 0.34 (upper line, representative value of d = 10 nm and r = 15 nm) to 0.17 (lower line, d = 10 nm and r = 30 nm). Angles are denoted with respect to the chain axis. (B) Experimentally measured orientation of the [111] direction of magnetosome crystals in magnetotactic bacteria (which corresponds to the direction of the magnetization) at the corresponding field strengths (same colors as in panel A). The large discrepancies obtained for 35 mT are explained in the text.

The theoretical model we developed presents a steady increase of α with increasing Ω (Figure 3A). At low field strength, the particles are nearly not following the external field, even for high angles (e.g., α(Ω = 90°, B = 20 mT) ≈ 15°) because the internal forces are larger than the external forces. The interactions between the magnetic moments of the magnetosomes stabilize the crystal orientation in its initial position. At high field strength, the particle orientation is nearly matching that of the external field (α(Ω = 90° ,B = 150 mT) ≈ 90°). In this case, the external forces become larger, and the interaction between the magnetosome dipole is no longer strong enough to hold them in place. In both cases, the theoretical results are only qualitatively similar to the experimental ones (the angles differ up to ca. 10°). For intermediate field strength (35 mT), a discrepancy of more than 70° is observed for Ω = 90°. Moreover, the change in the pattern of rotation that we observe experimentally appears to be abrupt rather than gradual as predicted by the model. While the magnetosomes follow almost exactly the rotation of the external field for a field strength of 35 mT, no rotation at all is seen for a field strength of 20 mT (Figure 3B) and even for 30 mT (see below).

To analyze the source of this discrepancy (Figure S4, Supporting Information), we used the internal magnetic field B_int as a fitting parameter. Quantitative agreement (with difference <5°) for B_ext = 150 mT is obtained if B_int is smaller than∼4 mT. Such a small value of B_int is obtained when the separation between neighboring magnetosomes is comparable to their diameter, a distance considerably larger than that observed in electron micrographs (Figure 1B). An opposing requirement is obtained for a good fit to the data for B_ext = 20 mT, namely, B_int > 40 mT. This value is not only considerably larger than the estimated value based on the EM images, but even exceeds B₀ ≈ 30 mT, which is the highest possible value within our model. These observations suggest two conclusions: (i) The torque opposing the rotation of the magnetosomes at weak external fields is probably not only of magnetic origin. Taking our original estimate of B_int ≈ 15 mT suggests a nonmagnetic contribution corresponding to an additional 25 mT, i.e., comparable to or even larger than the torque resulting from magnetic interactions. (ii) The opposing requirements for weak and strong fields suggest that there are structural differences in the arrangement or the molecular interactions of the magnetosome when the system is probed with different field strengths. A potential explanation is that the chain structure is disrupted by the field, e.g., breaking at least part of the molecular complexes responsible for this assembly. The abrupt change in the rotation behavior at about 30–35 mT suggests that the disruption happens at a critical field strength in this range.

Strong Fields Break the Magnetosome Chains

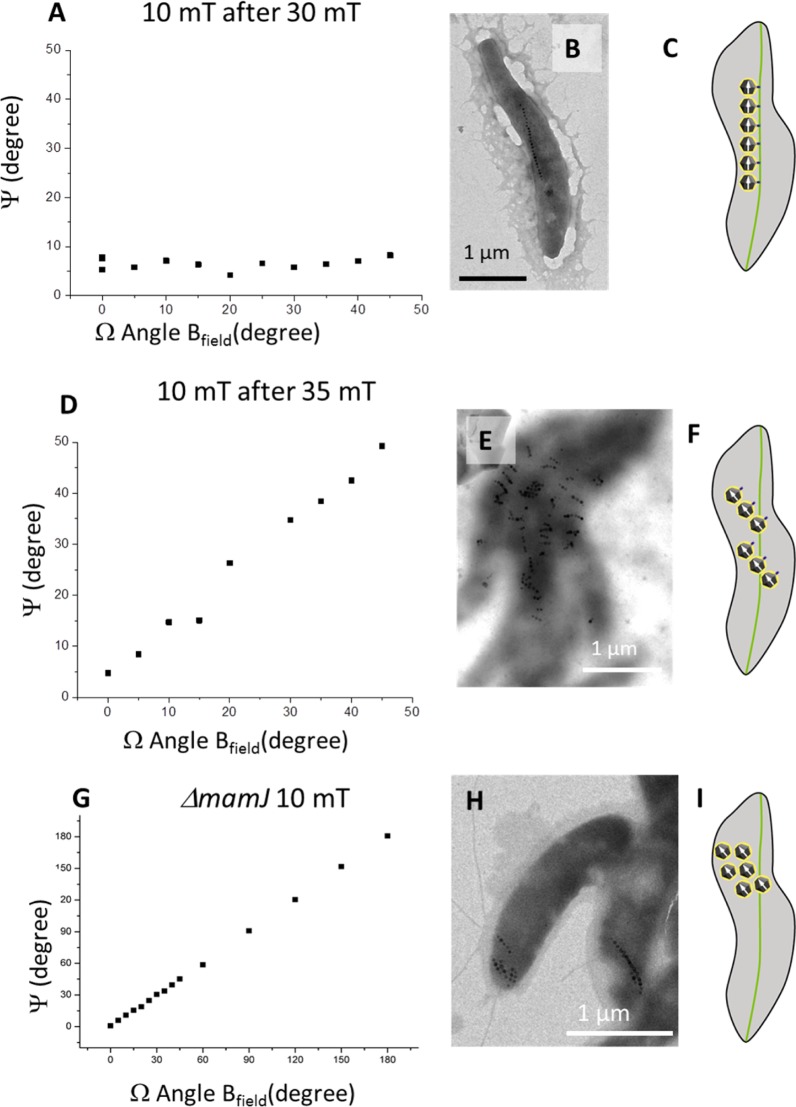
We performed a set of two consecutive experiments with different field strengths to test if strong fields disrupt magnetosome chains. After the cells are exposed to rotating fields with strengths either larger or smaller than 30 mT, a weak magnetic field (10 mT) is rotated around the sample (Figure 4). When an initial field weaker or equal to 30 mT is used, the orientation of the magnetosomes in their natural alignment remains unchanged during the whole process, and no rotation is observed when subsequently using a field strength of 10 mT (Figure 4A). By contrast, when we initially use 35 mT, a field strength at which we showed a compliance of the magnetic particle orientation with respect to field direction, we also observe a rotation when subsequently using 10 mT (Figure 4D). As shown before, 10 mT is initially not sufficient to change the magnetosome orientation.

Figure 4.

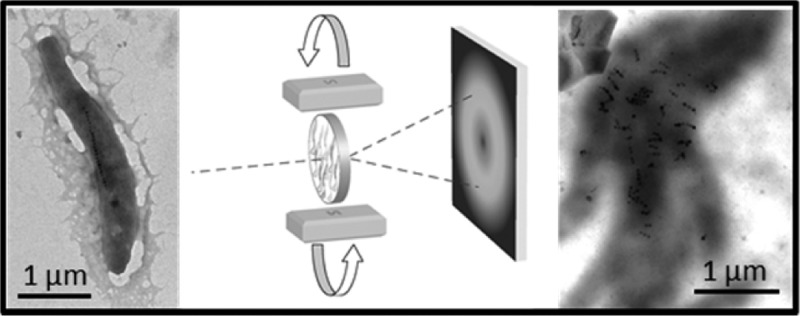
Measured angle of orientation of the magnetosomes as a function of the angle of the external field at 10 mT. When the initial experiment was performed at 30 mT (A), the magnetosome orientation is unchanged during the process. In this case, the TEM image shows that the chain has remained intact (B). Scheme of the observed situation in the wild-type cells: the magnetosomes are attached to the MamK filaments by the MamJ proteins (in blue) (C). When the initial field of 35 mT was used (D), the magnetosomes reorient and follow the external field. After cross-linking of the biological macromolecules, broken chains are observed (E). In this case, the interaction between MamJ and MamK is putatively disturbed as depicted in the scheme (F). For the ΔmamJ mutant, the magnetosomes reorient and follow the external field even directly at 10 mT (G). In addition, multiple, possibly short, chains not oriented along the long axis of the bacteria are observed (H) similar to what is imaged when chains of WT cells are broken (E) . The scheme (I) depicts the absence of MamJ and thereby the fact that the magnetosomes displacement is no longer restricted by the mamJ/MamK interaction, even at low field.

This confirms the hypothesis of a structural change, which is irreversible on the time scale of the experiment. We interpret this observation such that the magnetosome chains are destroyed after treatment with field strength above 30 mT. Indeed, if the magnetic coupling between the magnetosomes in the chain is absent, field strengths smaller than the initially observed 30 mT might suffice to rotate individual magnetosomes not stabilized by neighboring particles.

The bacteria are then imaged by EM after cross-linking of their internal structure by the addition of paraformaldehyde inside the gel, before (Figure 4B) and after (Figure 4E) treatment with a field strength of 35 mT applied at 90°. In the absence of treatment, the bacteria exhibit the usual chain alignment (Figure 4B). After treatment, however, the long magnetosome chains are absent (Figure 4E). Instead, small, fragmented chains of about 3 to 6 magnetosomes are observed, which are dispersed in the cells and oriented perpendicular to the long axis of the cell and thus parallel to the externally applied field. The electron micrographs clearly show that at least part of the molecular complexes responsible for the assembly are disrupted. However, if the bacteria are not cross-linked after such treatment, WT-like pattern are observed rather than fragmented chains, suggesting that the macromolecular scaffold is dynamic enough to rapidly reform. Fluorescence images of mCherry-MamK did not show any broken filamentous structure (Figure 1G,H). Thus, we conclude that the weakest link of the substructure is not MamK.

ΔmamJ Mutant Crystals Are Oriented by a Field of Low Strength

Next, we used a ΔmamJ mutant of MSR-1, which lacks the ability to assemble the magnetosomes in chains and form clusters instead.^33,34 XRD experiments with this mutant result in the orientation of the crystals in the direction of the applied field even at low field strength (Figure 4G). Therefore, the X-ray patterns of the mutants are similar to those obtained with wild-type cells either at high magnetic field strength or at low field after the application of a high field. In addition, EM images confirm that the mutants exhibit features similar to those of cells with broken chains after treatment at high field (Figure 4H). This suggests that disruption of MamJ or at least of the interaction between MamJ and MamK is responsible for the pattern observed in our experiment with wild-type cells (Figure 4F,I).

Mechanical Implications

Our observation of a threshold field strength around 30 mT can be used to obtain an estimation of the mechanical properties of the underlying biological determinant MamJ. Indeed, the torque applied by a magnetic field on a magnetic dipole is given by

4

The magnetic moment of a magnetosome particle with a radius of 20 nm is m = 1.6 × 10^–17 Am². Assuming a chain of 20 particles, the magnetic moment of the chain sums up to 3.2 × 10^–16 Am². A field of 30 mT results in a torque on the chain of τ_chain = 1 × 10^–17 Nm. At this field strength, the rotation of the crystals is altered, and no change in the localization of the filament is detected. This suggests that the filamentous backbone inside living magnetotactic bacteria is strong enough to resist such a torque.

The strong change from restricted rotation of the magnetosomes to complete alignment occurs between 30 and 35 mT. The torque generated on the magnetosomes by fields of 35 mT is sufficient to break MamJ or at least its interaction with MamK. The torque generated by a field of 30 mT on a single magnetosome is about τ = 4.9 × 10^–19 Nm. With τ = F × r, the torque can be converted into a force applied on the surface of the particle. In this case, a force of F = 24.5 pN is obtained. This value is comparable, but slightly lower than the reported rupture forces (of 40–80 pN) for the interaction of the actin-binding proteins filamin and α-actinin to actin that were obtained in vitro.⁷

In summary, we have studied the mechanical properties of the macromolecular complex involved in the magnetosome chain stabilization in magnetotactic bacteria in vivo. The inherent hierarchical structuring of the microorganisms enables the synthetic-reporter-free analysis of the system. Indeed, the magnetosomes take over the role of natural internal reporters. Elucidating the mechanical properties of such assemblies will pave the way toward the understanding of mechanical signaling and in this case even possibly of magnetoreception in higher organisms.

In addition, 1D magnetic devices have potential application in actuators, sensors, and electronics.^35,36 Specifically, magnetosomes and magnetosome chains represent a paradigm of biological 1D magnetic nanostructures and have therefore numerous bio- and nanotechnological applications.^37,38 Understanding the interaction between the magnetite crystals and their support is thus of primary importance since it allows the understanding of the physical forces and interactions exerted between crystals and biological components. This knowledge in turn is necessary for the design of hierarchical and multifunctional materials.

Supporting Information Available

Detailed experimental methods, additional theoretical considerations, supplementary figures, and author’s contributions. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^⊥ Universität Bayreuth, Lehrstuhl für Mikrobiologie, Universitätssstraße 30, 95447 Bayreuth, Germany.

The authors declare no competing financial interest.