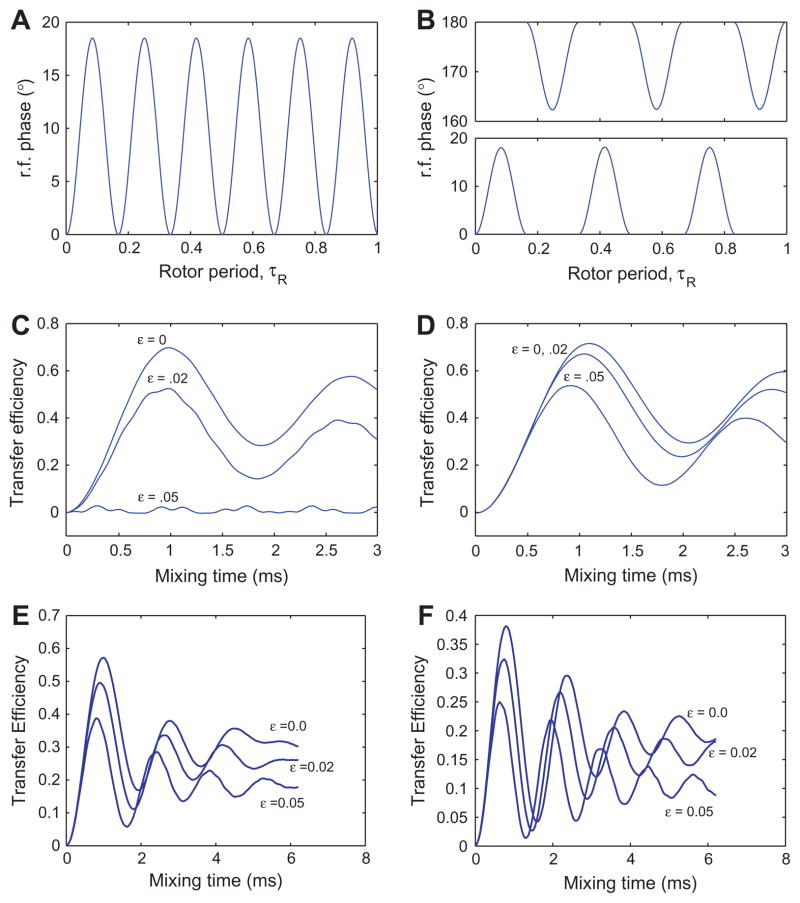
Fig. 1.
The top two panels show the phase of the rf irradiation as a function of time (in the units of τR) for the CMRR (A) and PAMORE (B) pulse sequences when C = 6ωr. The bottom two panels show numerical simulations of the transfer efficiency for the 13C–13C spin-pair, 1.52 Å apart in a powder sample subject to 8 kHz MAS, an external magnetic field corresponding to a 360 MHz (Larmor frequency for 1H) spectrometer and nominal rf-field strength on the 13C channel of 48 kHz, for the CMRR (C) and PAMORE (D) pulse sequences, for three different values of rf-inhomogeneity parameter, ε(0, .02, .05). Simulations use C = 6ωr, giving τc = 125/6 μs and rf-power of . The efficiency is reduced with increasing ε. In panel C at ε = .05, there is almost no transfer. Simulations were done with SPINEVOLUTION software [14]. In Fig. C and D, we assume spins on resonance with no CSA. In Fig. E and F, we simulate the performance of the PAMORE pulse sequence with phase modulation implemented as constant phases over interval of .2 (as in C and D) and 1.3 μs respectively. The later correspond to experimental realization shown in Figs. 3 and 5. The simulated transfer is for Iy → Sy, where I and S spins are Cα and CO, respectively. Carrier is placed on CO resonance with Cα and CO resonances at 35 and 170 ppm respectively. Chemical shift ansiotropy of 19.3 and 70.2 ppm and asymmetry parameter η = 1.225 and η = 1.05 are used for Cα and CO spins respectively. The Euler angles (α, β, γ) relating the chemical shielding tensors to the principle axis system of the dipolar tensor are and [12].