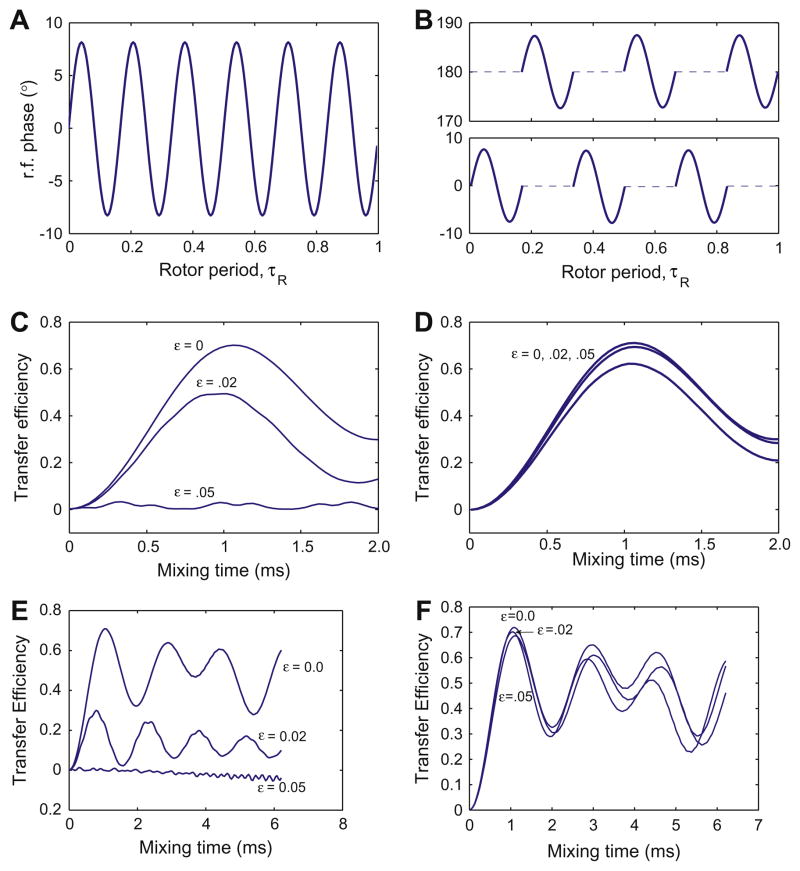
Fig. 4.

Panel A and B show the phase of the rf irradiation as a function of time (in the units of τ_R) for the Z-PAMORE recoupling element with and without phase alternation, respectively, when C = 6ω_r. In (5), this corresponds to θ = 0. Panel C and D show numerical simulations of the transfer efficiency, $\frac{\langle S_z\rangle }{\langle I_z\rangle }$, for the ¹³C–¹³C spin-pair, 1.52 Å apart in a powder sample subject to 8 kHz MAS, an external magnetic field corresponding to a 360 MHz (Larmor frequency for ¹H) spectrometer and nominal rf-field strength on the ¹³C channel of 48 kHz, for the phase modulations as shown in figure A and B respectively, for three different values of rf-inhomogeneity parameter, ε(0, .02, .05). Simulations use C = 6ω_r, giving τ_c = 125/6 μs and rf-power of ${\omega }_{rf}^C/2\pi =48\text{kHz}$. The efficiency is reduced with increasing ε much more rapidly in the absence of phase alternation. Simulations were done with SPINEVOLUTION software [14] and Fig. C and D, assume an ideal two spin system with no isotropic and anisotropic shifts. In Fig. E and F, we simulate the performance of the ZPAMORE pulse sequence without and with phase alternation with the carrier placed midway between C_α and CO resonances at 35 and 170 ppm respectively. The simulated transfer is for I_z → S_z, where I and S spins are C_α and CO respectively. Chemical shift ansiotropy of 19.3 and 70.2 ppm and asymmetry parameter η = 1.225 and η = 1.05 are used for C_α and CO spins respectively. The Euler angles (α, β, γ), relating the chemical shielding tensors to the principle axis system of the dipolar tensor are ${\mathrm{\Omega }}_{PC}^{{\mathrm{C}}_{\alpha }}=(-33.7,-95.3,48.92)$ and ${\mathrm{\Omega }}_{PC}^{\text{CO}}=(154.32,-2.9250,-106.8)$ [12]. Phase modulation is discretized over intervals of .2 μs.