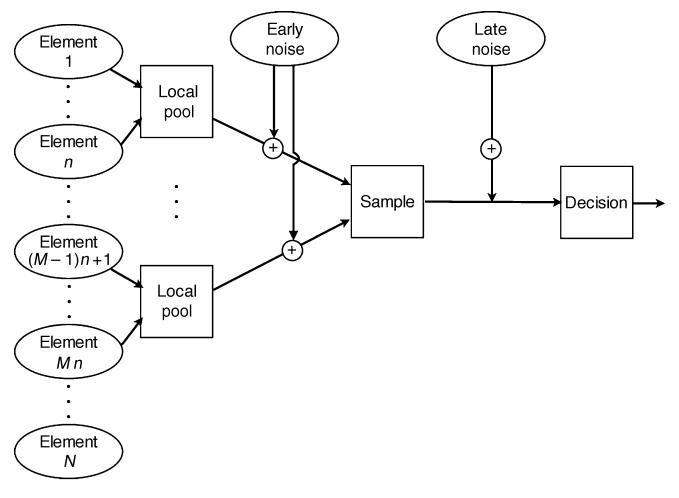
Figure 1. The inefficient, noisy estimator of texture statistics.

Intuition suggests that the visual noise added to neighboring, crowded elements is more likely to be correlated than that added to distant elements. This possibility is approximated here by pooling stimulus values (e.g., orientation or size) from n neighboring elements in an effectively noise-free way. An independent, identically distributed sample of “early” Gaussian noise is then added to each pool. M pools contribute to the observer’s decision statistic, which is also subject to perturbation by Gaussian noise (i.e., “late noise”). When, as in both the current study and Solomon (2010), texture elements are demonstrably uncrowded, we can assume n = 1, and efficiency can be defined as M/N. In this case, the “local pools” effectively compute local averages, but it is conceivable that they could compute some other statistic when n ≥ 2. Both the sample size M and the late noise may vary with the observer’s task, but—by definition—early noise may vary only with the stimulus. When combined, the two sources of noise comprise the total “equivalent noise” for the observer’s task, so called because its effects can be mimicked by perturbing the stimulus itself (Pelli, 1990).