Significance
The control of electron spin transport in molecular systems has been receiving lots of attention among different scientific communities because of possible applications in spintronics and understanding of the spin effects in biological systems. Recent experiments have demonstrated that α-helical protein acts as an efficient spin filter and the chiral-induced spin selectivity may be a general phenomenon. However, no spin selectivity was measured in single-stranded DNA above the experimental noise. In the present study, we propose a physical model to rationalize the above phenomena, and provide an unambiguous physical mechanism for spin-selective phenomenon observed in α-helical protein and for the contradictory behaviors between protein and single-stranded DNA. These results may facilitate engineering of chiral-based spintronic devices.
Keywords: spintronics, biological molecules, chirality, multiple transport pathways, spin-filtering effect
Abstract
We report on a theoretical study of spin-dependent electron transport through single-helical molecules connected by two nonmagnetic electrodes, and explain the experiment of significant spin-selective phenomenon observed in α-helical protein and the contradictory results between the protein and single-stranded DNA. Our results reveal that the α-helical protein is an efficient spin filter and the spin polarization is robust against the disorder. These results are in excellent agreement with recent experiments [Mishra D, et al. (2013) Proc Natl Acad Sci USA 110(37):14872–14876; Göhler B, et al. (2011) Science 331(6019):894–897] and may facilitate engineering of chiral-based spintronic devices.
Spintronics is a multidisciplinary field that manipulates the electron spin transport in solid-state systems and has been receiving much attention among the physics, chemistry, and biology communities (1–4). Recent experiments have made significant progress in this research field, finding that double-stranded DNA (dsDNA) molecules are highly efficient spin filters (5–7). This chiral-induced spin selectivity (CISS) is surprising because the DNA molecules are nonmagnetic and their spin-orbit couplings (SOCs) are small. Additionally, the CISS effect opens new opportunities for using chiral molecules in spintronic applications and could provide a deeper understanding of the spin effects in biological processes. For the above reasons, there has been considerable interest in the spin transport along various chiral systems including dsDNA (8–11), single-stranded DNA (ssDNA) (12–15), and carbon nanotubes (16). However, no spin selectivity was measured in the ssDNA above the experimental noise (5).
Very recently, spin-dependent electron transmission and electrochemical experiments were performed on bacteriorhodopsin—an α-helical protein of which the structure is single helical—embedded in purple membrane which was physisorbed on a variety of substrates (17). It was reported by means of two distinct techniques that the electrons transmitted through the membrane are spin polarized, independent of the experimental environments, implying that this α-helical protein can exhibit the ability of spin filtering. Meanwhile, a chiral-based magnetic memory device was fabricated by using self-assembled monolayer of another α-helical protein called polyalanine (18). All of these results seem to be inconsistent with previous experiments’ conclusions that the single-stranded helical molecules, such as ssDNA, may not polarize the electrons (5). We note that the electron transport/transfer has been widely investigated in many proteins (19–26). However, to our knowledge, the underlying physics is still unclear for spin-selective phenomenon observed in the α-helical protein and for the contradictory behaviors between the protein and the ssDNA.
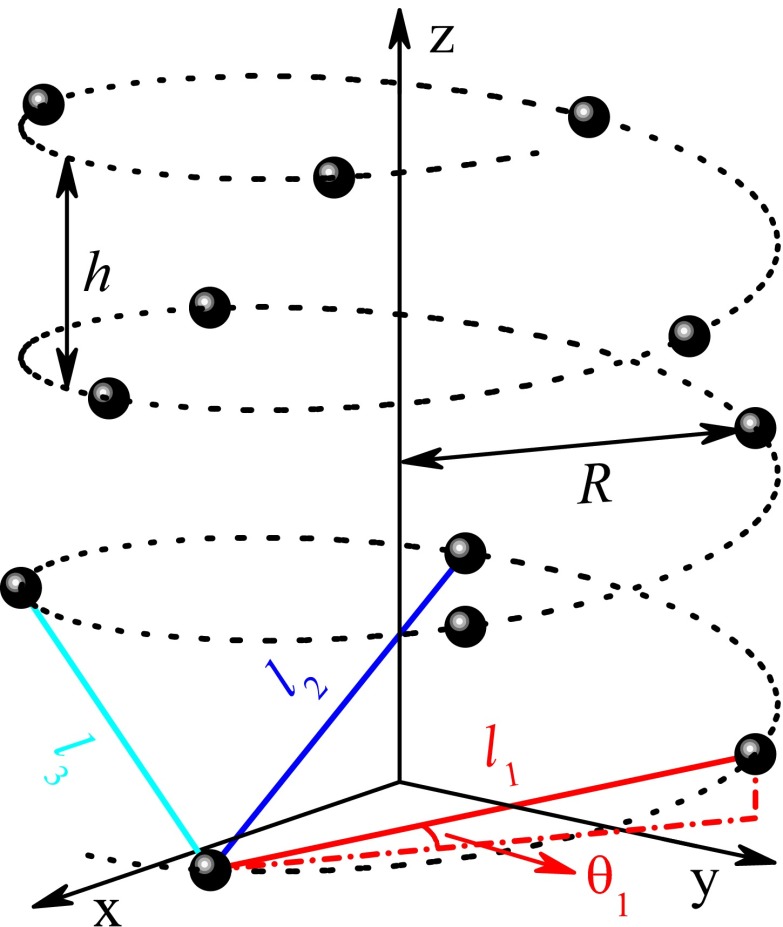
In this paper, we propose a model Hamiltonian to explore the spin transport through single-helical molecules connected by two nonmagnetic electrodes, and provide an unambiguous physical mechanism for efficient spin selectivity observed in the protein and for the contrary experimental results between the protein and the ssDNA. Our results reveal that the α-helical protein is an efficient spin filter, whereas the ssDNA presents extremely small spin filtration efficiency with the order of magnitude being 10−5, although both molecules possess single-helical structure as illustrated in Fig. 1, where the circles represent the amino acids (nucleobases) for the protein (ssDNA). The underlying physics is attributed to the intrinsic structural difference between the two molecules that the distance lj of the jth neighboring sites (e.g., sites n and n + j) increases much slower with increasing j for the protein than for the ssDNA, because the stacking distance Δh between the nearest neighbor (NN) sites is shorter in the protein. This can be seen from Table 1, which lists structural parameters including lj (j ≤ 6) for the α-helical protein and the regular B-form DNA. Then, the difference lj − l1 of j > 1 is much smaller in the protein. Consequently, for the protein, the long-range hopping, such as the second NN hopping and the third one, is comparable to the NN hopping, and the electrons can transport along the molecule via multiple pathways, while for the ssDNA, the long-range hopping is much weaker than the NN one and the electrons mainly move by NN hopping. This discrepancy leads to completely different spin-selective phenomena between the protein and the ssDNA.
Fig. 1.
Single-helical molecule with radius R and pitch h, where the circles (sites) denote the amino acids for protein and the nucleobases for DNA. Because of the electron wave function overlap, the electrons can hop between two neighboring sites with the Euclidean distance lj. Here, with Δφ and Δh being the twist angle and the stacking distance between the nearest neighbor sites, respectively. The space angle between the solid line and the x−y plane is defined as θj = arccos[2R sin (jΔφ/2)/lj].
Table 1.
Structural parameters of the α-helical protein and the regular B-form DNA
| Molecule | l1 | l2 | l3 | l4 | l5 | l6 | R | h | Δφ | Δh |
| Protein | 4.1 | 5.8 | 5.1 | 6.2 | 8.9 | 10.0 | 2.5 | 5.4 | 5π/9 | 1.5 |
| DNA | 5.5 | 10.7 | 15.2 | 19.0 | 22.0 | 24.4 | 7.0 | 34.0 | π/5 | 3.4 |
The distance (angle) is in unit Å (rad).
Results and Discussion
The spin transport along two-terminal single-helical molecules can be simulated by the Hamiltonian:
| [1] |
where , and and are, respectively, the kinetic and potential energies of the electrons at the molecular region, with the momentum operator and m the electron mass. The second term, , is the SOC Hamiltonian with c the speed of light and the Pauli matrices.
In what follows, we discretize and on the basis set constructed by the amino acids (nucleobases) with the amplitude of the electron wave function being ψn at site n. Then, the discretized form of is
| [2] |
where is the creation operator at site n of the molecule whose length is N; is the potential energy and is the jth neighboring hopping integral. It is reasonable that the wave function ψn decays exponentially on the distance in the potential barrier, i.e., , with l the distance from site n and lc the decay exponent. Then, by integrating tj along the straight line between two neighboring sites n and n + j (see Fig. 1), we obtain , which is similar to the Slater–Koster scheme, and lc can be determined by matching to first-principles calculations (27). Similarly, by calculating , the SOC Hamiltonian can be written as
| [3] |
where is the renormalized SOC, , and ; φn = nΔφ is the cylindrical coordinate of site n, and Δφ is the twist angle between the NN sites. We stress that in the case of small Δφ and the NN approximation, Eqs. 2 and 3 are reduced to our previous model (8).
Finally, describes the left (n < 0) and right (n > N) semiinfinite real electrodes and their couplings to the molecule. is the Hamiltonian of dephasing that occurs naturally in the experiments. For instance, the dephasing processes can be caused by the electron–phonon interaction and the electron–electron interaction. The electrons will also be scattered from the nuclear spins and the adsorbed impurities. In fact, previous works have clearly demonstrated the decoherence in the proteins (28–30). Such inelastic scatterings lead to the loss of phase memory of the electrons and can be simulated by connecting each site of the molecule to a Büttiker’s virtual electrode (8). Then, under the boundary condition that the net current across each virtual electrode is zero, the spin-up conductance G↑ and the spin-down one G↓ can be calculated by combining the Landauer–Büttiker formula and the nonequilibrium Green’s function (31). The spin polarization is defined as Ps = (G↑ − G↓)/(G↑ + G↓).
For the single-helical molecule, the potential energy is set to εn = 0 without loss of generality, the NN hopping integral t1 is taken as the energy unit, and the renormalized NN SOC is chosen as s1 = 0.12t1. Then, the NN SOC s1 cos(Δφ/2) of the protein and the ssDNA is 0.077t1 and 0.11t1, respectively, which are one order of magnitude smaller than the NN hopping integral. The absolute values of t1 and s1 may differ from one sample to another. The decay exponent is evaluated to be lc = 0.9 Å, which is close to the B-form DNA (27). For the real electrodes, the retarded self-energy can be calculated numerically with tm = 4t1 and τ = 2t1 (32). Because of the coupling to the virtual electrodes, the dephasing strength is taken as Γd = 0.06t1. As discussed below, the spin-filtering effect of the protein is significant in a very wide range of model parameters.
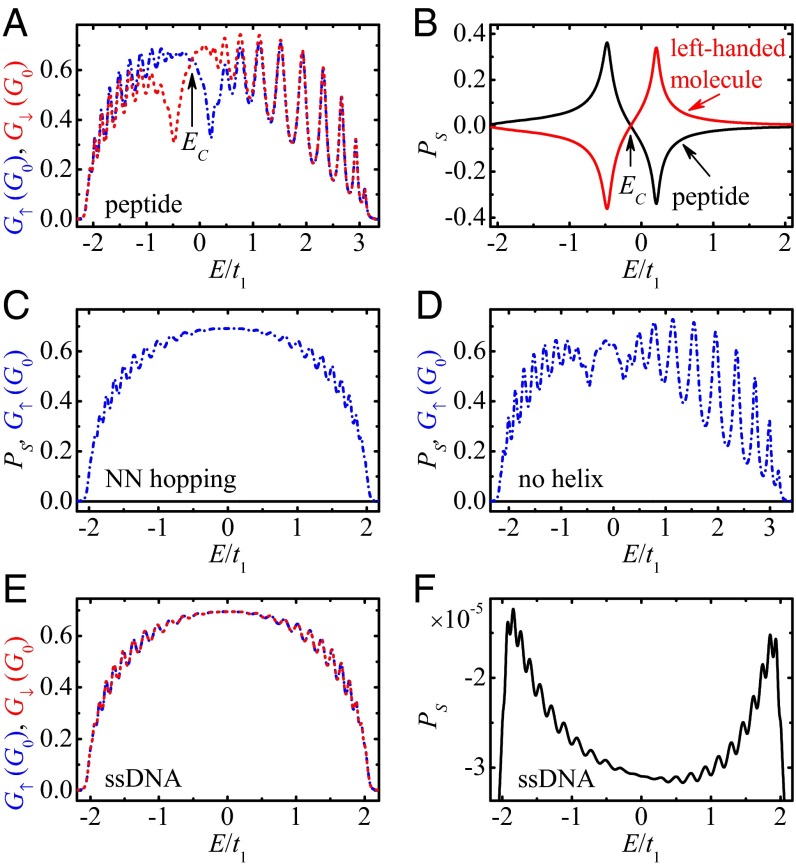
Fig. 2A displays the spin-up conductance G↑ (dash-dotted line) and the spin-down one G↓ (dashed line) vs. the Fermi energy E for the α-helical peptide whose length is N = 30, which approaches the height of the molecule patch (17). One can identify some important features. (i) Several sharp peaks are found in the transmission spectra for both spin-up and spin-down electrons (holes) due to the coherence of the system. (ii) Both G↑ and G↓ are asymmetric with respect to the line E = 0, because the long-range hopping breaks the electron–hole symmetry and shifts the “band center” Ec, below which the number of the electronic states equals that above Ec. As a result, the energy range of nonzero conductance is wider for E > Ec than for E < Ec. (iii) More importantly, G↑ is different from G↓, except for the band center Ec where G↑ = G↓. Consequently, the spin polarization Ps is nonzero for the peptide, as seen from the black line in Fig. 2B. The spin polarization of the peptide can reach the value 36.2%, which is larger than that measured in the experiment (17). Besides, Ps is positive for E < Ec, which refers to the electrons, and becomes negative for E > Ec, which corresponds to the holes. When the holes are propagating along the positive z axis (see Fig. 1), this process can be regarded as the electrons transmitting along the opposite direction, and hence the sign of is changed. Furthermore, by using the reflection symmetry, the right-handed peptide is transformed into the left-handed molecule, and the twist and space angles are changed from Δφ to −Δφ and from θj to π − θj while fixing the other model parameters. In this situation, the spin-up and spin-down conductances exchange with each other and Ps is reversed exactly, i.e., Ps(−Δφ, π − θj) = −Ps(Δφ, θj) (see the red line in Fig. 2B).
Fig. 2.
(A) Energy-dependent spin-up conductance G↑ (dash-dotted line), spin-down one G↓ (dashed line) and (B) spin polarization Ps (black line) for the peptide in realistic situation, where the red line denotes Ps for the left-handed molecule. Ps (solid line) and G↑ (dash-dotted line) in the absence (C) of the long-range hopping and (D) of the helical symmetry. (E) G↑, G↓ and (F) Ps for the ideal ssDNA. Here, G0 = e2/h is the quantum conductance. The model parameters are N = 30, s1 = 0.12t1, lc = 0.9 Å, and Γd = 0.06t1. The peptide can be an efficient spin filter, whereas the ideal ssDNA exhibits extremely small Ps.
To explore the underlying physics of high Ps found in the peptide, we consider the spin transport in the absence of the long-range hopping and of the helical symmetry, respectively, where the other parameters are the same as in Fig. 2A. Fig. 2C shows Ps and G↑ without any long-range hopping, i.e., tj = sj = 0 if j > 1. In this case, there exists only one transport pathway, called the NN hopping, in the system. Then, by using a unitary transformation (8), the Hamiltonian can be switched into a spin-independent one and hence Ps is exactly zero, regardless of the other parameters. In contrast, in the presence of the long-range hopping, the electrons can transport along single-helical molecules via multiple pathways, such as the NN hopping and the second NN hopping. In the protein, the difference lj − l1 is quite small, so some long-range electronic parameters are comparable to the NN ones, e.g., t2 ∼ 0.16t1, t3 ∼ 0.32t1, s2 ∼ 0.16s1, and s3 ∼ 0.32s1. This indicates that in the protein, there exist multiple transport pathways, which is similar to the dsDNA, where the electrons can propagate not only along the single-helical chain but also within the base pairs (8). In this situation, the spin precession induced by the SOC varies for different transport pathways, and high Ps could appear in the peptide (Fig. 2B). Fig. 2D shows Ps and G↑ in the absence of the helical symmetry, i.e., Δφ = 0 and θj = π/2. One can see that Ps is strictly zero here, for whatever the values of the SOC, the long-range hopping, and the dephasing. These indicate that both the helical symmetry and the long-range hopping are key ingredients for nonzero spin polarization observed in the peptide.
Since the helical symmetry is a key factor to yield spin-selective electron transmission, we first focus on the ideal case that the ssDNA still holds the regular B-form structure. Fig. 2 E and F show, respectively, G↑/↓ and Ps for the ideal ssDNA. Since the distance difference lj − l1 is much larger in the ssDNA, the long-range electronic parameters, which decay exponentially with lj − l1, are much smaller than the NN ones, i.e., tj ≪ t1 and sj ≪ s1, and the electrons mainly propagate via the NN hopping, and the spin transport property will present distinct features compared with the peptide. (i) The transmission peaks are smoother in the ssDNA, because almost all of the electrons experience the inelastic scattering from each site and the dephasing effect will be more pronounced. (ii) There is no observable difference between G↑ and G↓ of the ssDNA, and Ps is very small, with the order of magnitude being 10−5. Notice that the ssDNA does not possess a well-defined secondary structure. Thus, the distorted ssDNA with twist angle disorder is also discussed by considering the rigid sugar-phosphate backbone (see SI Text), where both the radius R and the NN distance l1 are fixed (8, 33). When the twist angle disorder is incorporated, the ssDNA deviates from the regular B-form structure and its helicity can somewhat be destroyed. In this situation, Ps remains about 10−5 (SI Text and Fig. S1B). This value of Ps is too small to be detected experimentally, and the ssDNA cannot act as a spin filter, in excellent agreement with the experiment (5) and the theoretical work (8).
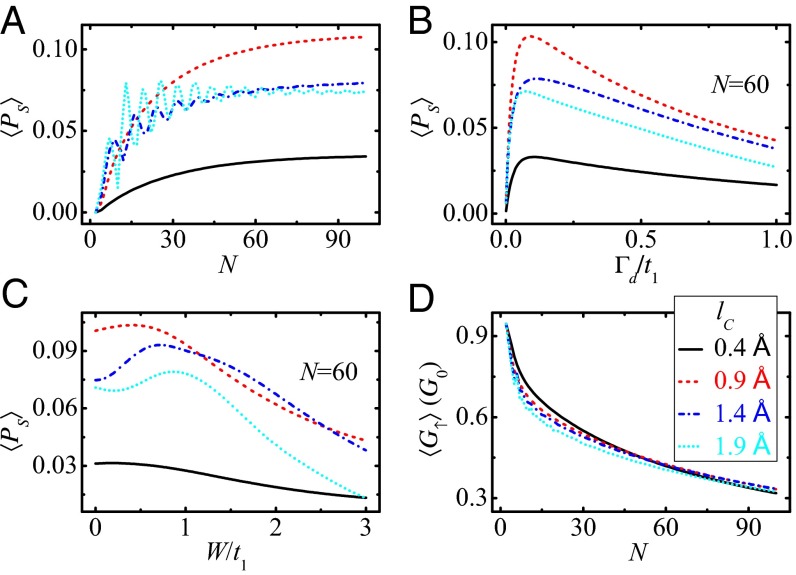
In what follows, we investigate the spin transport properties of the peptide in a wide range of model parameters by calculating the averaged spin polarization 〈Ps〉, which is obtained by averaging Ps over the lower energy band of E < Ec. Fig. 3A plots the length-dependent 〈Ps〉 for several values of the decay exponent lc. In the region of small lc, 〈Ps〉 increases with N and the rising slope is gradually declined (see the solid and dashed lines in Fig. 3A), while in the region of large lc, 〈Ps〉 presents oscillating behavior as N is enhanced, and the oscillation amplitude is reduced by increasing N or by decreasing lc (see the dash-dotted and dotted lines in Fig. 3A).
Fig. 3.
Averaged spin polarization 〈Ps〉 and averaged conductance 〈G↑〉 of the peptide as functions of different model parameters. (A) 〈Ps〉 vs. the length N, (B) 〈Ps〉 vs. the dephasing strength Γd with N = 60, (C) 〈Ps〉 vs. the diagonal disorder strength W with N = 60, and (D) 〈G↑〉 vs. N. The different lines denote different lc, and the other parameters are the same as those in Fig. 2A. The spin-filtering effect of the peptide is significant in a wide range of model parameters.
Fig. 3B plots 〈Ps〉 vs. the dephasing strength Γd. A crossover is observed in all curves of 〈Ps〉–Γd that 〈Ps〉 increases with Γd at first and is then slowly declined by further increasing Γd, irrespective of lc. Actually, the dephasing has two effects that compete with each other. On the one hand, in the presence of the dephasing, each site of the molecule is connected to a Büttiker’s virtual electrode and the two-terminal device is switched into multiterminal one naturally. In other words, the dephasing promotes the openness of the system and can generate the spin filtering (8, 34). One expects that nonzero Ps could also be found in the peptide by connecting to multiple real electrodes in the absence of the dephasing, because the real electrode is similar to the Büttiker’s virtual one. On the other hand, the dephasing leads to the loss of the electron phase memory and reduces the spin polarization. Consequently, 〈Ps〉 decreases with Γd in the strong dephasing regime and tends to zero when Γd → ∞.
We then study the influence of disorder on the spin transport along the peptide, where the disorder may originate from distinct amino acids and is simulated by considering stochastic on-site potential energies that are uniformly distributed in [−W/2, W/2], with W the disorder strength. Fig. 3C shows 〈Ps〉 vs. W. Here, the results are obtained from a single disorder configuration and are similar for other disorder configurations. One can see that the spin selectivity is very robust against the disorder. 〈Ps〉 can increase slightly with W for W < t1 and is then slowly decreased for W > t1. When the disorder strength is W = 3t1, 〈Ps〉 ∼ 4.3% for the peptide of lc = 0.9 Å. Fig. 3D shows the averaged conductance 〈G↑〉 vs. N. With increasing N, the electrons experience more inelastic scattering and thus 〈G↑〉 decreases with N. Nevertheless, 〈G↑〉 is still very large for N = 100. Therefore, we conclude that the α-helical peptide/protein can be an efficient spin filter not only for large Ps and G↑ but also for the robustness against the disorder.
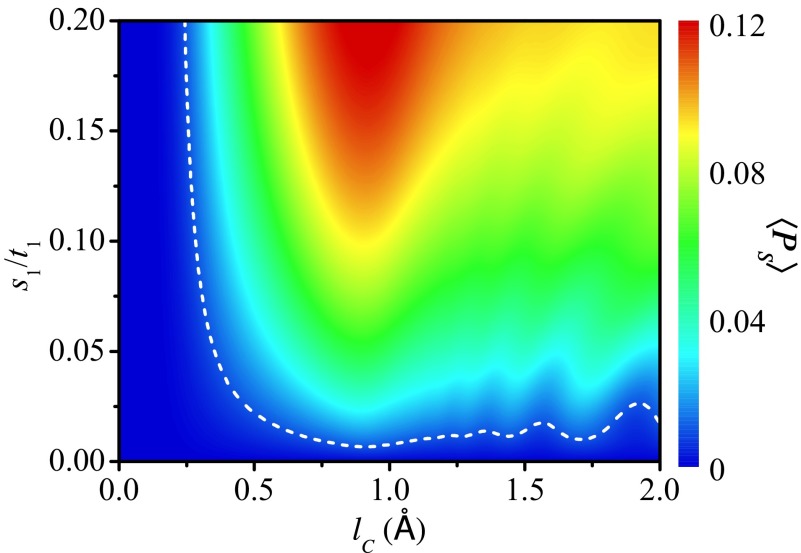
Fig. 4 displays the 2D plot of 〈Ps〉 as functions of lc and s1, where the dashed line of 〈Ps〉 = 1.0% is shown for reference. One notices that the spin-filtering effect is pronounced in a wide range of lc and s1, even in the region of weak SOC. For example, when Å and s1 = 0.02t1, Ps can be 22.5% and 〈Ps〉 ∼ 2.7%; when lc = 0.5 Å and s1 = 0.12t1, Ps can be 8.8% and 〈Ps〉 ∼ 5.0%. Even for very small values of s1 = 0.004t1 and 0.007t1, Ps can be 6.4% and 10.6%, respectively (SI Text and Fig. S2A). Since the SOC is a driving force of spin polarization, 〈Ps〉 is exactly zero when s1 = 0 and is increased by increasing s1. In the region of small lc, the long-range hopping is very weak and there exists only one dominant transport pathway. In this case, the spin polarization is too small to be detected experimentally, just like the ssDNA. By increasing lc, the long-range hopping becomes comparable with the NN hopping such that there exist multiple transport pathways, and the spin-filtering effect will be enhanced. In the region of very large lc, the long-range hopping becomes dominant. Then, a considerable part of the electrons will be scattered by only a few sites of the molecule, i.e., the effective length of the molecule for these electrons is very short. As a result, the spin polarization will be slightly weakened. The optimal range of lc to observe high Ps may be [0.6, 3.0] Å for the peptide of N = 60.
Fig. 4.
A 2D plot of the averaged spin polarization 〈Ps〉 vs. the decay exponent lc and the renormalized NN SOC s1 for the peptide with N = 60 and Γd = 0.06t1. The dashed line represents 〈Ps〉 = 1.0%. The spin selectivity of the peptide is also significant in a wide range of lc and s1, even in the region of weak SOC.
Conclusions
In summary, a model Hamiltonian is proposed to explore the spin transport along two-terminal single-helical molecules and the contrary experimental results between the α-helical protein and the single-stranded DNA are elucidated. Our results indicate that the α-helical peptide/protein is an efficient spin filter, whereas the single-stranded DNA exhibits very small spin polarization. The spin-filtering effect of the protein is significant in a very wide range of model parameters and is very robust against the diagonal disorder and the dephasing. This model is also suitable for describing the electron and spin transport properties of other single-helical molecules.
Supplementary Material
Acknowledgments
This work was financially supported by National Basic Research Program of China under Grant 2012CB921303, National Natural Science Foundation of China under Grant 11274364, and Postdoctoral Science Foundation of China under Grant 2013M540153.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. J.R.W. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1407716111/-/DCSupplemental.
References
- 1.Žutić I, Fabian J, Das Sarma S. Spintronics: Fundamentals and applications. Rev Mod Phys. 2004;76(2):323–410. [Google Scholar]
- 2.Sanvito S. Molecular spintronics. Chem Soc Rev. 2011;40(6):3336–3355. doi: 10.1039/c1cs15047b. [DOI] [PubMed] [Google Scholar]
- 3.Sinova J, Žutić I. New moves of the spintronics tango. Nat Mater. 2012;11(5):368–371. doi: 10.1038/nmat3304. [DOI] [PubMed] [Google Scholar]
- 4.Naaman R, Waldeck DH. Chiral-induced spin selectivity effect. J Phys Chem Lett. 2012;3(16):2178–2187. doi: 10.1021/jz300793y. [DOI] [PubMed] [Google Scholar]
- 5.Göhler B, et al. Spin selectivity in electron transmission through self-assembled monolayers of double-stranded DNA. Science. 2011;331(6019):894–897. doi: 10.1126/science.1199339. [DOI] [PubMed] [Google Scholar]
- 6.Xie Z, et al. Spin specific electron conduction through DNA oligomers. Nano Lett. 2011;11(11):4652–4655. doi: 10.1021/nl2021637. [DOI] [PubMed] [Google Scholar]
- 7.Senthil Kumar K, Kantor-Uriel N, Mathew SP, Guliamov R, Naaman R. A device for measuring spin selectivity in electron transfer. Phys Chem Chem Phys. 2013;15(42):18357–18362. doi: 10.1039/c3cp53089b. [DOI] [PubMed] [Google Scholar]
- 8.Guo AM, Sun QF. Spin-selective transport of electrons in DNA double helix. Phys Rev Lett. 2012;108(21):218102. doi: 10.1103/PhysRevLett.108.218102. [DOI] [PubMed] [Google Scholar]
- 9.Guo AM, Sun QF. Enhanced spin-polarized transport through DNA double helix by gate voltage. Phys Rev B. 2012;86(3):035424. [Google Scholar]
- 10.Rai D, Galperin M. Electrically driven spin currents in DNA. J Phys Chem C. 2013;117(26):13730–13737. [Google Scholar]
- 11.Eremko AA, Loktev VM. Spin sensitive electron transmission through helical potentials. Phys Rev B. 2013;88(16):165409. [Google Scholar]
- 12.Yeganeh S, Ratner MA, Medina E, Mujica V. Chiral electron transport: Scattering through helical potentials. J Chem Phys. 2009;131(1):014707. doi: 10.1063/1.3167404. [DOI] [PubMed] [Google Scholar]
- 13.Gutierrez R, Díaz E, Naaman R, Cuniberti G. Spin-selective transport through helical molecular systems. Phys Rev B. 2012;85(8):081404. [Google Scholar]
- 14.Medina E, López F, Ratner MA, Mujica V. Chiral molecular films as electron polarizers and polarization modulators. EPL. 2012;99(1):17006. [Google Scholar]
- 15.Gersten J, Kaasbjerg K, Nitzan A. Induced spin filtering in electron transmission through chiral molecular layers adsorbed on metals with strong spin-orbit coupling. J Chem Phys. 2013;139(11):114111. doi: 10.1063/1.4820907. [DOI] [PubMed] [Google Scholar]
- 16.Diniz GS, Latgé A, Ulloa SE. Helicoidal fields and spin polarized currents in carbon nanotube-DNA hybrids. Phys Rev Lett. 2012;108(12):126601. doi: 10.1103/PhysRevLett.108.126601. [DOI] [PubMed] [Google Scholar]
- 17.Mishra D, et al. Spin-dependent electron transmission through bacteriorhodopsin embedded in purple membrane. Proc Natl Acad Sci USA. 2013;110(37):14872–14876. doi: 10.1073/pnas.1311493110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ben Dor O, Yochelis S, Mathew SP, Naaman R, Paltiel Y. A chiral-based magnetic memory device without a permanent magnet. Nat Commun. 2013;4:2256. doi: 10.1038/ncomms3256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jin Y, Friedman N, Sheves M, He T, Cahen D. Bacteriorhodopsin (bR) as an electronic conduction medium: Current transport through bR-containing monolayers. Proc Natl Acad Sci USA. 2006;103(23):8601–8606. doi: 10.1073/pnas.0511234103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Prytkova TR, Kurnikov IV, Beratan DN. Coupling coherence distinguishes structure sensitivity in protein electron transfer. Science. 2007;315(5812):622–625. doi: 10.1126/science.1134862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schlag EW, Sheu SY, Yang DY, Selzle HL, Lin SH. Distal charge transport in peptides. Angew Chem Int Ed Engl. 2007;46(18):3196–3210. doi: 10.1002/anie.200601623. [DOI] [PubMed] [Google Scholar]
- 22.Beratan DN, Balabin IA. Heme-copper oxidases use tunneling pathways. Proc Natl Acad Sci USA. 2008;105(2):403–404. doi: 10.1073/pnas.0711343105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cordes M, Giese B. Electron transfer in peptides and proteins. Chem Soc Rev. 2009;38(4):892–901. doi: 10.1039/b805743p. [DOI] [PubMed] [Google Scholar]
- 24.Arikuma Y, Nakayama H, Morita T, Kimura S. Electron hopping over 100 Å along an α helix. Angew Chem Int Ed Engl. 2010;49(10):1800–1804. doi: 10.1002/anie.200905621. [DOI] [PubMed] [Google Scholar]
- 25.Gao J, et al. Electron transfer in peptides: The influence of charged amino acids. Angew Chem Int Ed Engl. 2011;50(8):1926–1930. doi: 10.1002/anie.201003389. [DOI] [PubMed] [Google Scholar]
- 26.Sepunaru L, Friedman N, Pecht I, Sheves M, Cahen D. Temperature-dependent solid-state electron transport through bacteriorhodopsin: Experimental evidence for multiple transport paths through proteins. J Am Chem Soc. 2012;134(9):4169–4176. doi: 10.1021/ja2097139. [DOI] [PubMed] [Google Scholar]
- 27.Endres RG, Cox DL, Singh RRP. Colloquium: The quest for high-conductance DNA. Rev Mod Phys. 2004;76(1):195–214. [Google Scholar]
- 28.Morita T, Kimura S. Long-range electron transfer over 4 nm governed by an inelastic hopping mechanism in self-assembled monolayers of helical peptides. J Am Chem Soc. 2003;125(29):8732–8733. doi: 10.1021/ja034872n. [DOI] [PubMed] [Google Scholar]
- 29.Skourtis SS, Balabin IA, Kawatsu T, Beratan DN. Protein dynamics and electron transfer: electronic decoherence and non-Condon effects. Proc Natl Acad Sci USA. 2005;102(10):3552–3557. doi: 10.1073/pnas.0409047102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Giese B, Graber M, Cordes M. Electron transfer in peptides and proteins. Curr Opin Chem Biol. 2008;12(6):755–759. doi: 10.1016/j.cbpa.2008.08.026. [DOI] [PubMed] [Google Scholar]
- 31.Datta S. Electronic Transport in Mesoscopic Systems. Cambridge, UK: Cambridge Univ Press; 1995. [Google Scholar]
- 32.Lee DH, Joannopoulos JD. Simple scheme for surface-band calculations. II. The Green’s function. Phys Rev B. 1981;23(10):4997–5004. [Google Scholar]
- 33.Gore J, et al. DNA overwinds when stretched. Nature. 2006;442(7104):836–839. doi: 10.1038/nature04974. [DOI] [PubMed] [Google Scholar]
- 34.Sun QF, Xie XC. Spontaneous spin-polarized current in a nonuniform Rashba interaction system. Phys Rev B. 2005;71(15):155321. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.