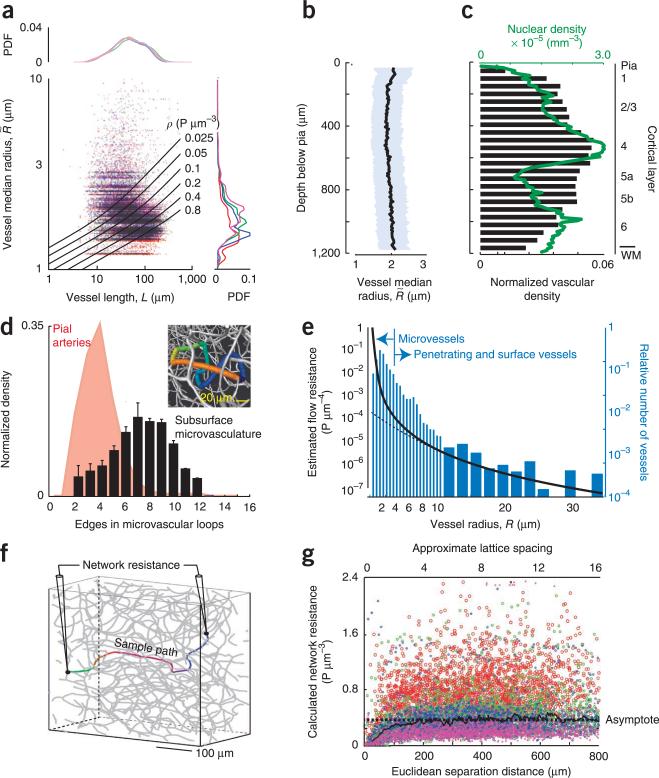
Figure 2.

Analysis of the local geometry and topology of the microvasculature. (a) Scatter plot as a function of the total length of each vessel, defined as $L_{mn}={\sum }_k{l}_{mn}^{\left(k\right)}$, and the median radius, denoted as R_mn. The lines are plots of constant fluid resistance (equation in Edge resistance of Online Methods). Data are from 101,992 edges across four brains. The line plots are probability distribution functions (PDFs) for different brains, found by projecting the data across all lengths (right) or radii (top). (b) Plot of the mean radius across all segments in an axial slice as a function of depth. (c) Plot of the density of the microvasculature and neuronal density as a function of depth. The vascular density in an axial slice was defined as the fractional length of all edges in an axial slice. WM, white matter. (d) PDF of the number of branches in different microvascular loops. Data are from 59,909 loops across four brains. The bars denote 1 s.d. For comparison, the distribution of branches in the surface pial network is reproduced⁵. The inset is a close up of a section of a vectorized network showing only the microvascualture. The colored edges highlight a loop that consists of eight branches, each with a distinct color. (e) Plot of the flow resistance per unit length as a function of vessel radius; the total resistance is found by multiplying by the length, in micrometers. Note the marked increase in resistance for radii below ~5 μm, where the Hagen-Poiseuille law (dashed line) no longer holds. The concurrent histogram shows the distribution of vessel radii for all vessels. (f) Schematic of the numerical probe of total resistance between two vertices in the network. (g) Scatter plot of the resistance between pairs of vertices (1,000 pairs per brain across four brains) as a function of the Euclidian distance between the vertices. The asymptote highlights the constant value averaged across all data sets, indicative of a three dimensional lattice. The slope, (3.0 ± 4.4) × 10⁻⁵ (mean ± 95% confidence interval, found with robust linear regression), was not significant.