Multi-Surgeon, Multi-Site Validation of a Trajectory Planning Algorithm for Deep Brain Stimulation Procedures

Abstract

Deep brain stimulation, which is used to treat various neurological disorders, involves implanting a permanent electrode into precise targets deep in the brain. Reaching these targets safely is difficult because surgeons have to plan trajectories that avoid critical structures and reach targets within specific angles. A number of systems have been proposed to assist surgeons in this task. These typically involve formulating constraints as cost terms, weighting them by surgical importance, and searching for optimal trajectories, in which constraints and their weights reflect local practice. Assessing the performance of such systems is challenging because of the lack of ground truth and clear consensus on an optimal approach among surgeons. Due to difficulties in coordinating inter-institution evaluation studies, these have been performed so far at the sites at which the systems are developed. Whether or not a scheme developed at one site can also be used at another is thus unknown. In this article, we conduct a study that involves four surgeons at three institutions to determine whether or not constraints and their associated weights can be used across institutions. Through a series of experiments, we show that a single set of weights performs well for all surgeons in our group. Out of 60 trajectories, our trajectories were accepted by a majority of neurosurgeons in 95% of the cases and the average acceptance rate was 90%. This study suggests, albeit on a limited number of surgeons, that the same system can be used to provide assistance across multiple sites and surgeons.

I. Introduction

Deep brain stimulation (DBS) procedures, which are widely used to treat patients suffering from neurological disorders such as Parkinson’s disease, tremor, or dystonia [1], require placing a permanent four contact electrode in specific deep brain nuclei. Multiple studies have indicated that precise planning of the trajectory is necessary to avoid psychological and motor side effects or complications such as hemorrhage. Comprehensive reviews of risks associated with the procedure can be found in [2–3]; the latter reports a risk of hemorrhage ranging from 0.3% to 10% per patient, depending on the site at which the procedure is performed. At leading clinical sites, a 1% risk of intracranial hemorrhage associated with permanent neurological deficit is currently considered to be the norm. Planning the procedure is thus a task that requires expertise, and a review of the literature shows that a number of approaches have been proposed over the years to assist surgeons in selecting trajectories for neurosurgery in general and for DBS procedures in particular. In 1997, Vaillant et al. [4] quantified the risk of a candidate trajectory using a weighted sum of the voxel costs manually assigned according to the tissue significance along a trajectory. A decade later, Brunenberg et al. [5] approached the problem again. They evaluated the risk of an automatic trajectory using the maximum voxel cost, defined as the minimum distance to vessels and ventricles. The set of all possible trajectories that satisfied the cost criteria defined as distance thresholds to each structure was then displayed to surgeons for them to choose from. This was followed by the work of Navkar et al. [6], who attempted to facilitate the path selection process by overlaying color-coded risk maps on a rendered surface of the patient’s head. Shamir et al. [7] proposed to account for both the weighted sum of voxel costs and the maximum voxel cost with respect to vessels and ventricles along the trajectory, and combined the individual costs of each structure with risk levels defined by surgeons. In a more comprehensive framework, Essert et al. [8] formalized various surgical rules as separate geometric constraints and aggregated them into a global cost function for path optimization. Following a similar idea, Bériault et al. [9] defined constraints using multi-modality images and modeled the trajectory as a cylinder.

While these methods suggest the feasibility of developing reliable computer-assisted planning systems, assessing their performance remains challenging, as no universal ground truth exists. Qualitative evaluations have involved user-experience questionnaire about effectiveness of the interactive path selection software by neurosurgeons [5–6]. Recently, Shamir et al. [7] and Essert et al. [8] have quantitatively compared the safety of automatic trajectories with manual ones using their distances to critical structures. Essert et al. [8] also reported the global and individual costs between those two types of trajectories on 30 cases, which, as stated in the paper, may favor the automatic approach that is designed to minimize these cost values. Bériault et al. [9] performed not only a quantitative evaluation similar to others [7–8], but also a qualitative validation where the automatic trajectories were rated against one set of manual trajectories by two neurosurgeons for 14 cases retrospectively. More recently, Bériault et al. [10] tested their method prospectively on 8 cases in a study where the system proposed five trajectories in the first round. If none of these were found acceptable, the system was initialized interactively by surgeons up to three times to compute a local optimal trajectory each time. The surgeon could then choose either one of the system-generated trajectories or a trajectory selected manually in the normal delivery of care. Out of these 8 cases on which this method was evaluated, one of the five initial system-generated solutions was selected for five cases, a manually initialized but automatically computed solution was selected for one case, one case was planned manually by the surgeon and for the last case both solutions were deemed equivalent.

Importantly, even though all the current automatic trajectory computation algorithms involve a cost function with multiple terms modeling surgical constraints and the selection of weights for each of these terms, no study has explored whether or not individual surgeon preferences would necessitate the adjustment of weights or even the constraints. It is thus not known whether one could develop a system that could be used by a multitude of surgeons at multiple sites or if some type of training would be required when a system is fielded at a new site. In this article, we report on a number of experiments we have performed as an extension of previous work [11] to begin answering these questions both retrospectively and pseudo-prospectively. In the rest of the article, we first provide details about the data, the cost function, and the training method we have used. The various experiments we have performed to study whether or not one could capture surgeon preferences and if these were of clinical significance are described next. This is followed by a description of pseudo-prospective studies we have performed with 3 experienced movement disorder surgeons (one affiliated with our institution, one with Wake Forrest University, and one with Stanford University) who collectively perform in excess of 200 cases a year. We subsequently present the results we have obtained for each of these experiments. These results are discussed and avenues for future investigations are presented in the last section of this article.

II. Methods

A. Data

Thirty DBS patients with bilateral implantations in the subthalamic nucleus (STN) are included in this study, for a total of 60 distinct trajectories. All subjects provided informed consent prior to enrollment. For each subject, our dataset includes MR T1-weighted images without and with contrast agent (MR T1(-C)), and the target position at which the implant has been surgically placed. The MRIs (TR: 7.9 ms, TE: 3.65 ms, 256×256×170 voxels, with voxel resolution 1×1×1 mm³) were acquired using the SENSE parallel imaging technique from Philips on a 3T scanner. The MR T1-C is rigidly registered to the MR T1 prior to trajectory optimization with a standard intensity-based technique that uses Mutual Information [12–13] as its similarity measure.

B. Trajectory Planning

Our approach involves formulating surgical constraints as individual cost terms and finding the optimal trajectory in a limited search space based on a cost function that aggregates those cost terms.

1) Formulation of Surgical Constraints

We gathered a number of constraints expressed as rules through extensive discussions with the two experienced movement disorder neurosurgeons affiliated with our institution. These rules are based on factors including safety, esthetic, and lead orientation with respect to the target structures and are similar but not identical to constraints used by others. For example, constraints such as minimizing the path length [8], minimizing overlap with caudate [9] and maximizing the orientation of the electrode depending on target shape [8], were not considered significant by our surgeons and thus not included in our system. Some of these rules cannot be violated while others lead to trajectories that are less desirable when violated. Using these rules we designed a cost function that contains hard constraints, i.e., constraints that cannot be violated, and soft constraints, i.e., constraints that penalize the trajectories more as the extent to which they are violated increases.

a) Rule 1 (Burr hole)

The entry point should be posterior to the hairline for czosmetic reasons and anterior to the motor cortex to avoid side effects.

This is incorporated in our algorithm by limiting the generation of candidate trajectories within an allowable bounding box defined on a skin-air interface mesh.

b) Rule 2 (Vessels)

The trajectory should stay away from vessels to minimize the risk of hemorrhage.

This is modeled as a soft constraint that penalizes trajectories that are closer than 3 mm from a vessel, with the corresponding cost term f₂ defined as follows:

$$f_2=\{\begin{array}{cc}\hfill (3-d_2)/(3-d_{2_{\text{min}}})\hfill & \hfill \text{if}{d}_2<3\hfill \\ \hfill 0\hfill & \hfill \text{if}{d}_2\ge 3\hfill \end{array}$$ (1)

where d₂ is the Euclidean distance from the trajectory to the vessels and d_2min is the minimum value of d₂ over the set of trajectories being evaluated for one case. A hard constraint is also defined which sets the total cost of a trajectory to be maximum if it penetrates a vessel.

c) Rule 3 (Ventricle)

Ventricles are structures that should not be perforated by the trajectory, while it is desirable to stay close to them to favor approaches that maximizes the coverage of the region of interest in the STN.

This is modeled through both a soft constraint that penalizes trajectories that are further than 2 mm to the ventricles, and a hard constraint that sets the total cost of a trajectory to be maximum if it is closer than 2 mm. The corresponding cost term f₃ for the soft constraint is defined as follows:

$$f_3=(d_3-2)/d_{3_{\text{max}}}-2),\text{if}{d}_3\ge 2$$ (2)

where d₃ is the Euclidean distance to the ventricles and d_3max is the maximum value of d₃ over the set of trajectories being evaluated for one case.

d) Rule 4 (Sulci)

It is unsafe to cross sulci because small vessels that are invisible on preoperative imaging are often present at the base of the sulci.

This is modeled as a soft constraint that penalizes trajectories that intersect the cortical surface at the base of the sulci. The cost term for this constraint, f₄, is defined as follows:

$$f_4=(d_{4_{\text{max}}}-d_4)/(d_{4_{\text{max}}}-d_{4_{\text{min}}})$$ (3)

where d₄ is a distance quantity to the sulci, and d_4min, d_4max are the minimum and maximum value of d₄ over the set of trajectories being evaluated respectively. The search area defined by the bounding box in Rule 1 is large enough to cover both sulcal and gyral regions, so that trajectories with f₄ approaching 1 intersect with sulci and trajectories with f₄ approaching 0 intersect with gyri. Further details on the computation of d₄ are provided later in this section.

e) Rule 5 (Suture)

Some neurosurgeons prefer the entry point to be near the coronal suture. This is modeled as a soft constraint that penalizes entry points that are located posteriorly or anteriorly from the middle of our allowable entry region, which is used as an approximation of the coronal suture. The cost term for this constraint, f₅, is defined as follows:

$$f_5=d_5/d_{5_{\text{max}}}$$ (4)

where d₅ is the Euclidean distance from the entry point of a trajectory to the suture, and d_5max is the maximum value of d₅ among all trajectories being evaluated.

f) Rule 6 (Thalamus)

Intersecting the lateral edge of the thalamus is desired by some surgeons when targeting the STN because it can be used as an electrophysiological landmark before reaching the target (this was expressed as a desirable trajectory property by one of the two surgeons at our institution).

This is modeled as a soft constraint that penalizes trajectories passing through the thalamus for less than one millimeter, with the corresponding cost f₆ defined as follows:

$$f_6=\{\begin{array}{cc}\hfill 1-d_6\hfill & \hfill \text{if}{d}_6<1\hfill \\ \hfill 0\hfill & \hfill \text{if}{d}_6\ge 1\hfill \end{array}$$ (5)

where d₆ is the length of the trajectory passing through the thalamus.

Cost function

The overall cost function, f_total, is a weighted sum of the individual cost terms associated with each of the soft constraints 2–6 we have defined. It also contains the hard constraints that are part of Rule 2 and Rule 3:

$$f_{\text{total}}=\{\begin{array}{cc}\hfill {\sum }_{i=2}^6{w}_i{f}_i\hfill & \hfill \text{if}{d}_2\ge 0\cap d_3\ge 2\hfill \\ \hfill 1\hfill & \hfill \text{otherwise}\hfill \end{array}\text{s.t.}\{w_i\}\ge 0,{\sum }_{i=2}^6{w}_i=1$$ (6)

where {d_i} are the distance quantities discussed above, and {w_i} are the values used to weigh the relative importance of each cost term. The method we use to obtain those weights is described in detail in the next section. All cost terms {f_i} are normalized, and the {w_i} are forced to be positive and their sum equal to 1. The overall cost f_total thus ranges from 0 to 1. If a trajectory hits a vessel, i.e., when d₂ < 0, or if a trajectory is closer than 2 mm to the ventricles, i.e., when d₃ < 2, then f_total is set to its maximum value. Otherwise, f_total is equal to the weighted sum of the cost terms.

2) Path Optimization

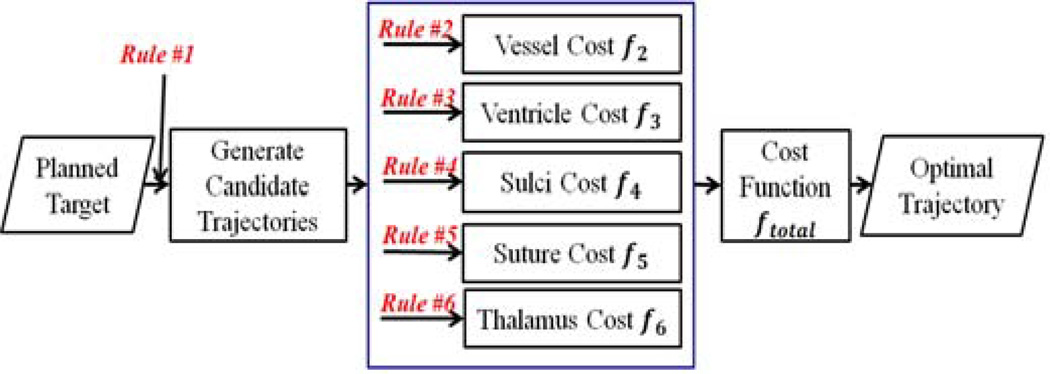
The path optimization process is an exhaustive search that consists of generating all candidate trajectories in a specific search space, computing the cost for each trajectory based on the cost function described above and finding the trajectory with the lowest cost, as illustrated in Fig. 1.

Fig. 1.

Overview of the path optimization process.

a) Path Generation

Each trajectory is modeled as a linear segment with a common target point and can be uniquely represented by its entry point located on the skin-air interface. This interface is a dense triangulated mesh with vertices representing possible entry points, and is obtained automatically by extracting the isosurface of the patient’s MR T1 after smoothing using the marching cubes algorithm [14] and then filtering out extraneous components.

The allowable entry region specified by Rule 1 is determined by projecting 4 points that have been selected manually by one neurosurgeon on one T1-weighted reference volume onto the patient’s head surface. This reference volume is registered to the corresponding patient volume using non-linear registration and the transformation that registers these volumes is used to project the points. Those four points defines a tetrahedron that bounds the region, and all vertices within this region on the skin-air interface are considered to be candidates. This set of candidate entry points typically consists of 2000 points separated by an average distance of 1 mm and serves as the constrained search space in which the optimal solution is found.

b) Cost Computation

Several rules (2, 3, 4 and 6) involve anatomical structures therefore their segmentations are required to compute the cost function. Vessels were identified by thresholding the difference image created by subtracting the MR T1 from T1-C within the skull region. Ventricles and thalamus were segmented by combining atlas-based segmentations from four atlases using STAPLE [15]. From those segmentations distance maps were computed with a fast marching method algorithm [16]. These were then used to calculate the distance between a trajectory and the various structures using the technique described by Noble et al. [17]. All non-rigid registrations were performed with the Adaptive Bases Algorithm [18].

The distance to the sulci, d₄, is computed in several steps, as illustrated in Fig. 2. First, the cortical surface is extracted using the LongCruise tool [19] (represented schematically by the colored curve). Then the deepest intersection point of the trajectory with this surface is found (shown as a star in Fig. 2). Vertices on the surface mesh that fall within N neighbor edge connections from this point are identified (indicated by dots in the same figure) and projected onto the trajectory to compute a signed distance from the intersection point to the projected points (positive inside the cortex, negative outside). The distance d₄ is a weighted average of those distance values, where the weights are defined to be the reciprocal of the number of points with the same neighbor edge connections so that points with approximately equal geodesic distance to the intersection point contribute equally. As can be seen in Fig. 2, d₄ is negative when intersecting a valley (i.e., a sulcus), is around zero when intersecting neither a peak nor valley, and is positive when intersecting a peak (i.e., a gyrus). Thus, f₄ is minimized when a trajectory intersects the cortical surface once through the top of a gyrus.

Fig. 2.

A 2D illustration of d₄. The curve represents the cortical surface and the lines represent candidate trajectories, all color coded by this sulci distance, d₄, where blue and red indicate lower and higher values respectively. The intersection points are indicated by stars and neighbor points by dots. From left to right, the average projection distance for each trajectory is negative, nearly zero, and positive, respectively.

III. EXPERIMENTS

We conducted a set of experiments, first retrospectively and internally with two surgeons at our institution and then pseudo-prospectively with two additional surgeons at external institutions. In this article, we define a pseudo-prospective experiment to be the selection of a trajectory as it would be done in clinical practice but without actually performing the procedure (more details on the way the experiments were performed are provided below). All experiments have been performed with the research version of the FDA cleared surgical planning system used clinically by all four neurosurgeons called WayPoint Navigator that is distributed by FHC, Inc. Bowdoin, ME, USA.

A. Retrospective, internal studies

The retrospective studies were performed by the two co-author neurosurgeons affiliated with our institution and subsequently referred to as surgeons A and B. Surgeon-specific weighting parameters were learned prior to any evaluation experiments using two sets of training volumes, one set per surgeon. To do this, we collected 10 pairs of images (T1 and T1-C) of patients operated on by surgeon A and another 10 operated on by surgeon B, all with bilateral implantation. For each of these volumes, the planned trajectories of both left and right sides selected by the surgeons in the normal delivery of care were available. These images and trajectories constitute the training sets, leading to 20 training trajectories from 10 patients per surgeon. Surgeon-dependent weights for our algorithm were determined heuristically and iteratively as follows. First, initial weight values were set according to the relative importance of the constraint, as stated by the surgeon. Then, automatically generated and manually selected trajectories were presented simultaneously in the surgical planning system to the surgeons who were blind to the way the trajectories were generated. The surgeons were asked to compare the trajectories using a four level comparative scale. If the trajectory being evaluated was chosen, i.e., if it better matched the surgeon’s preferences than the one chosen manually, it was classified as “Excellent”. If the surgeon was not able to determine which one was superior, e.g., if they were too close to each other, it was rated as “Equivalent”. If the trajectory under evaluation was not chosen but could still be used clinically, i.e., it was considered to be safe, it was classified as “Acceptable”, and otherwise was classified as “Rejected”. A computed trajectory was considered to be successful if rated “Acceptable” or better. Based on this surgeon’s feedback, weights were manually adjusted and the experiment repeated until each surgeon ranked all his training trajectories as at least acceptable, i.e., safe. This required four iterations. Once these parameters were estimated, they were fixed and used for all evaluation experiments.

To test our method with weights obtained in the training phase, we acquired another 10 image sets of patients operated on by surgeon B, all with bilateral implantation, for which the planned trajectories selected by surgeon B in the normal delivery of care were available. To obtain manual trajectories on the same set of image volumes, surgeon A was asked to select a trajectory manually on both sides of each of these volumes as if performing the procedure. These 10 volumes as well as both surgeons’ manual trajectories constitute the testing set, leading to 20 testing trajectories per surgeon. These manual trajectories were used in the various experiments described below. Evaluation of a trajectory in these experiments is achieved as described in the training session, i.e., the surgeons were asked to rate the trajectory against their own manual one without knowing the trajectories’ provenance with the four-level comparative rating scale described earlier.

The goals of our retrospective validation experiments were threefold. First, test whether or not we could estimate surgeon-specific parameter values that would lead to acceptable trajectories for the surgeon for whom the parameters were tuned. Second, evaluate whether or not surgeon-specific weighting parameters were indeed necessary. Third, test whether or not one surgeon would prefer trajectories generated automatically or by another surgeon, i.e., would automatic trajectories appear any different to a surgeon than trajectories selected manually by another experienced surgeon. The following experiments were performed to answer these questions.

1) Experiment 1: evaluation of the trajectories computed based on surgeons’ own preferences

The goal of the first experiment is to assess the degree to which the weighting factors optimized for each neurosurgeon effectively capture their preferences. The surgeon is asked to evaluate the trajectories computed by our method using his own preferences against his own clinical ones.

2) Experiment 2: evaluation of the trajectories computed based on other surgeons’ preferences

The goal of the second experiment is to assess the benefit of using surgeon-specific parameters. The surgeon is asked to evaluate the trajectories computed by our method using the weight values estimated for the other surgeon against his own clinical ones.

Results of experiment 1 and 2, detailed in the next section, led us to the conclusion that the set of weights optimized for surgeon B, could be used to pursue our validation study. Thus the computed trajectories evaluated in the following experiments are all generated by this set of weights.

3) Experiment 3: evaluation of the trajectories manually picked by other surgeons

The goal of the third experiment is to assess if automatically generated trajectories are distinguishable from trajectories manually selected by another surgeon. Each surgeon was presented with a choice between his trajectory and the trajectory manually selected by the other surgeon. The results of this experiment are compared to the results of the experiments in which each surgeon is presented with a choice between the automatically generated trajectory and his manual trajectory. The automatically generated trajectories for surgeon A are the same as those generated for him in experiment 2 and trajectories computed for surgeon B are the same as those evaluated in experiment 1, because, as discussed above, the weight values optimized for surgeon B were used for both surgeons in this experiment.

B. Pseudo-prospective studies

We define the pseudo-prospective scenario as putting the surgeons in the same conditions as a prospective scenario but using retrospective cases, i.e., we ask the surgeon to redo plans on patients that already underwent the surgery. Because in this study we focus on evaluating the trajectories, we fix the target point to be the clinical target point chosen during the real plan. To be more specific, for each case, surgeons were provided with a single trajectory. If they thought the trajectory was adequate to be used clinically, it was labeled as “Acceptable”; otherwise, it was labeled as “Rejected”. In this case, the surgeons would adjust it to make it useable and provide cause(s) for rejection. The two surgeons at our site evaluated and interacted with the trajectories on a laptop running the planning system as they would clinically. This typically involves checking the trajectory along its length in orthogonal views and in a “bird’s eye view”, i.e., in slices that are reformatted to be perpendicular to the trajectory. Surgeons were allowed to modify the trajectory to check whether or not a better one could be found. The surgeons at remote sites followed the same process but the computer was accessed remotely and its desktop shared. Although the goal of our pseudo-prospective study is to test in clinical conditions whether or not our algorithm could be used to assist the surgeon in selecting an optimal trajectory, we first investigate whether or not surgeons behave differently when choosing between two trajectories or when deciding to accept or reject a single trajectory. We do this by presenting surgeons A and B with the automatic trajectories they were presented in experiment 2 for surgeon A and in experiment 1 for surgeon B. We then extend our analysis to the multisite evaluation using a larger dataset.

4) Experiment 4: evaluation of the computed trajectories in pseudo-clinical setting within internal site

In this experiment, we put surgeons A and B into clinical conditions to test the automatic trajectories computed with surgeon B’s weights. We present each surgeon with 20 trajectories computed for the volumes in the testing set and ask them to either accept or reject the trajectories. These trajectories are the same as those presented to surgeon A in experiment 2 and surgeon B in experiment 1.

5) Experiment 5: evaluation of the computed trajectories in pseudo-clinical setting among multi-institutional surgeons

In this last experiment, we tested the automatic algorithm on the complete set of patients, i.e., on 60 trajectories. These trajectories were evaluated by one surgeon affiliated with Vanderbilt University, one with Stanford University, and one with Wake Forest University. Because the weights used to generate these trajectories were estimated to capture surgeon B’s preferences, he was completely eliminated from this pseudo-prospective experiment to avoid any bias.

As several constraints are based on the distance to specific structures, their under- or over-segmentation could affect our results. To avoid this potential confounding factor and because the focus of this paper is not on the validation of the segmentation algorithms, prior to experiment 5, we verified the segmentations of structures including ventricles and veins around the ventricles and refined them if needed.

IV. RESULTS

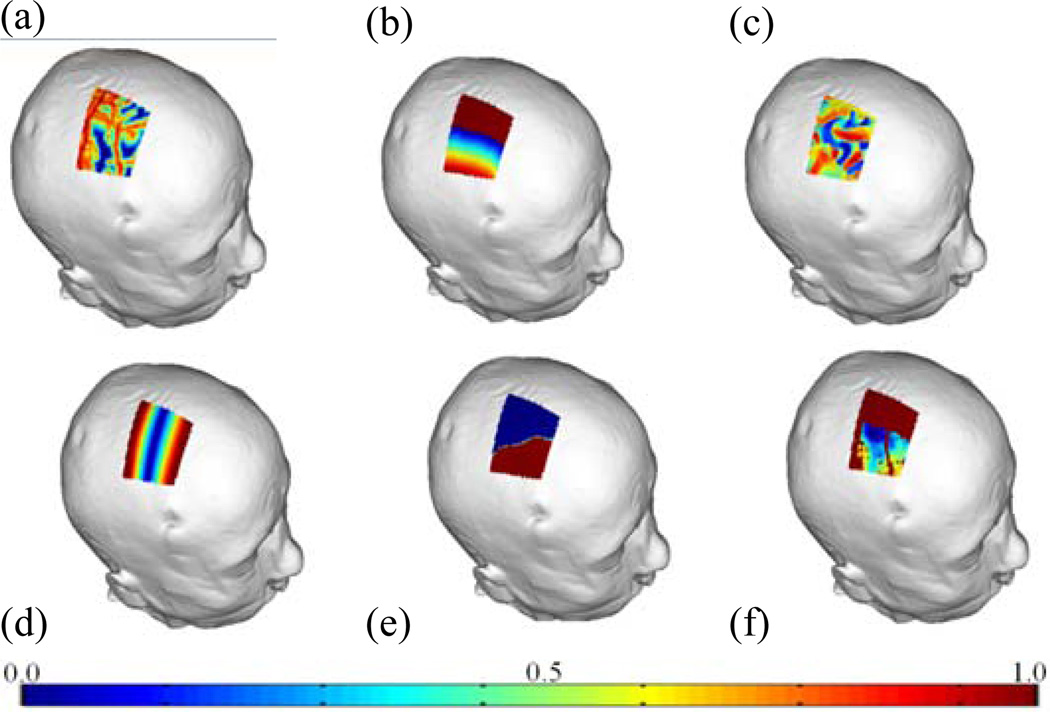
Parameter selection was carried out internally for surgeons A and B. For surgeon A, weighting parameters were chosen through the training process to be 0.18 for f₂, 0.18 for f₃, 0.35 for f₄, 0.24 for f₅, 0.05 for f₆. For surgeon B, weighting parameters were 0.20 for f₂, 0.27 for f₃, 0.40 for f₄, 0.13 for f₅, 0.00 for f₆. For illustration purposes, Fig. 3 shows for one case color maps that convey the costs associated with entry points within the allowable search region (blue = low cost, red = high cost). Panels (a)–(e) show individual costs and (f) shows the overall cost. Fig. 4 shows a manual trajectory (green) and two computed trajectories rated against this manual one for one case, with one rated as excellent (blue), and the other rejected (red). The rejected trajectory is closer to the sulcus, which is the reason for rejection. The trajectory rated as excellent is further away from vessels compared to the manual trajectory.

Fig. 3.

Color maps showing the cost for (a) f₂, the vessel cost; (b) f₃, the ventricle cost; (c) f₄, the sulci cost; (d) f₅, the suture cost; (e) f₆, the thalamus cost; (f) f_total, the total cost. (blue = low cost, red = high cost)

Fig. 4.

Manual trajectory (green), trajectory rated as excellent (blue), and trajectory rated as rejected (red), both being rated against the manual one. The surrounding structures include the ventricles (yellow), vessels (cyan), and the cortical surface (magenta). (a) a global view; (b) zoomed in view around the ventricular surface; (c) zoomed in view around the cortical surface.

Results for experiment 1 in which we assess the degree to which these weighting factors effectively capture the neurosurgeon’s preferences are presented in Fig. 5. For surgeon A, 25% of the 20 available test cases are rated as excellent, 50% as equivalent, 15% as acceptable, and 10% as rejected, while for surgeon B, 25% are rated as excellent, 10% as equivalent, 50% as acceptable, and 15% as rejected. Acceptance rates of 90% and 85% for surgeons A and B suggest that the surgeon’s preferences were reasonably captured in the weighting parameters.

Fig. 5.

Rating distribution of the trajectories computed using the surgeon's own set of weights for surgeons A (left) and B (right). Red represents the percentage of cases being rejected and light, medium, dark blue represents the percentage of cases rated as acceptable, equivalent, and excellent respectively.

Results for experiment 2 in which we assess the benefit of using surgeon’s specific parameters are shown in Fig. 6. This figure shows the results of the rating experiments conducted with surgeons A (left) and B (right). The light blue columns represent rating scores for the trajectories computed using the same surgeon’s set of weights and dark red for those computed using the other surgeon’s set of weights. For each surgeon, 15 out of the overall 20 cases ended up having the same rating scores between the trajectories computed using the two sets of weights. Only cases when these two rating scores were different are shown in this figure. The left panel shows that surgeon A consistently prefers trajectories computed using surgeon B’s weights and rated all of those trajectories better than the ones computed using his own weights. In the right panel, the plot shows that surgeon B rejected several trajectories computed using surgeon A’s weights and in general prefers his own set of weights. This suggests that the set of weighting parameters chosen for surgeon B is acceptable for both surgeons. Results obtained with this experiment led us to continue our analysis with only the set of weights optimized for surgeon B.

Fig. 6.

Pairwise comparison of rating scores. Left: experiment conducted by surgeon A; right: experiment conducted by surgeon B. Light blue represents the rating for the trajectory computed using the same surgeon’s set of weights and dark red indicates the rating for the trajectory computed using the other surgeon’s set of weights. Only cases that resulted in different rating between the two trajectories are shown.

The results of experiment 3 in which we assess whether or not a surgeon has a preference for automatically generated trajectories over trajectories selected manually by another surgeon are shown in Fig. 7. Results obtained with surgeon A are plotted in the left panel and those obtained with surgeon B in the right panel. For each surgeon we show the distribution of ratings for the other surgeon’s manual trajectories on the left and the distribution of ratings for the trajectories computed using surgeon B’s weights on the right. This figure shows that surgeon A tends to prefer the automatic trajectories over surgeon B’s manual trajectories and surgeon B rejected fewer automatic trajectories than trajectories produced manually by surgeon A. As is the case for our pseudo-prospective study (see below), the most frequent reason for rejecting an automatic trajetory is its position relative to the sulci.

Fig. 7.

Rating distributions of trajectories evaluated by surgeons A (left) and B (right). For each surgeon the ratings of the other surgeon’s manual trajectories are shown in the left and those of computed trajectories are shown in the right. Red represents the percentage of cases being rejected and light, medium, dark blue represents the percentage of cases rated as acceptable, equivalent, and excellent respectively.

To quantitatively evaluate automatic trajectories against manual ones, we compare vessel, ventricle, sulci, suture, and overall cost values obtained with each approach as well as the distances to the vessels and ventricles as was done in [7–9]. Table I reports means, standard deviations, minima and maxima for these quantities. To test whether or not differences are statistically significant, we also perform a Wilcoxon paired two-sided signed rank test and we report p values. Results show that automatically generated trajectories are further away from the vessels, as desired. For the ventricles, the automatic method leads to lower cost values even though the mean distance is lower for surgeon A than for the automatic approach. This is because several of surgeon A’s manal trajectories are closer to the ventricles than the 2 mm specified in Rule 3. This violates the hard constraint, thus raising the cost. This hard constraint is also violated for one automatic trajectory because in these experiments trajectories were computed with the automatic segmentations but the statistics are computed with the manually validated and edited segmentations. Automatically generated trajectories lead to lower cost for the sulci and lower suture costs for surgeon B. The overall cost is also statistically significantly lower for the automatic approach. However, as noted by Bériault et al. [9], these numbers have to be interpreted with care. Indeed, they only show that an automatic method is generally better at finding a minimum in an analytically defined function than a human operator. They do not show whether or not this function truly captures the decision-making process of a trained neurosurgeon. Ultimately, the safety and clinical acceptability of automatically generated trajectories needs to be assessed by asking experienced surgeons to review and rate each of them, which is done in experiments 4 and 5.

TABLE I.

DISTANCES TO VESSELS AND VENTRICLES AND ALL THE COST TERMS FOR TRAJECTORIES COMPUTED WITH SURGEON B’s WEIGHTS AND MANUAL TRAJECTORIES BY SURGEONS A AND B

		Vessel distance	Vessel cost	Ventricle distance	Ventricle cost	Sulci cost	Suture cost	Total cost
Automatic	Mean ± STD	4.50 ± 3.86	0.08 ± 0.13	3.80 ± 1.80	0.28 ± 0.29	0.10 ± 0.08	0.22 ± 0.27	0.17 ± 0.29
	[Min, Max]	[0.24, 15.14]	[0.00, 0.68]	[0.46, 7.05]	[0.01, 1.00]	[0.00, 0.26]	[0.01, 1.00]	[0.00, 1.00]
A’s Manual	Mean ± STD	3.38 ± 4.13	0.29 ± 0.33	3.69 ± 2.90	0.46 ± 0.36	0.35 ± 0.21	0.16 ± 0.12	0.48 ± 0.40
	[Min, Max]	[−0.19, 15.22]	[0.00, 1.00]	[−3.98, 8.91]	[0.01, 1.00]	[0.11, 0.73]	[0.03, 0.50]	[0.06, 1.00]
B’s Manual	Mean ± STD	3.67 ± 4.10	0.23 ± 0.29	4.30 ± 1.62	0.34 ± 0.26	0.24 ± 0.15	0.24 ± 0.15	0.29 ± 0.31
	[Min, Max)	[−0.44, 15.31]	[0.00, 1.00]	[0.46, 7.31]	[0.07, 1.00]	[0.00, 0.56]	[0.00, 0.56]	[0.01, 1.00]
Automatic V.S. A’s p-value		0.0089	0.0081	0.5372	0.1092	0.0001	0.4186	0.0029
Automatic V.S. B’s p-value		0.0925	0.0533	0.2111	0.3659	0.0029	0.2276	0.0063

Top three rows: mean, standard deviations, minima, and maxima of all the testing cases; bottom two rows: p values of the statistical tests performed between the automatic trajectories and manual trajectories. P values that are smaller than 0.05 are marked in red bold.

In experiment 4, where the surgeons were asked to either accept or reject the trajectory they were presented with, surgeon A rejected 3 trajectories and surgeon B 7. Fig. 8 shows the rating scores obtained for these rejected trajectories in experiments 1 and 2 when surgeons were evaluating the trajectories against their own manual selections. Over the trajectories that were rejected in this experiment, only 2 were rejected in the retrospective studies.

Fig. 8.

Rating scores of the cases rejected by surgeons under the pseudo-prospective scenario, evaluated by surgeons A (left) and B (right).

Table II presents the results of experiments 5. It shows that, on average, 90% of the automatic trajectories were accepted in our pseudo-prospective experiment using 60 trajectories. Fig. 9 reports the percentage of trajectories that were accepted by all three surgeons, by two surgeons, and by one surgeon as well as the fraction of trajectories rejected by all surgeons.

TABLE II.

ACCEPTANCE RATE FOR INDIVIDUAL NEUROSURGEONS (A, C, D) AND OVERALL IN EXPERIMENT 5

Surgeon A	Surgeon C	Surgeon D	Average
95.00%	83.33%	91.67%	90.00%
(57 / 60)	(50 / 60)	(55 / 60)	(54 / 60)

Fig. 9.

Voting distribution according to the trajectory’s acceptation/rejection status, i.e., accepted by all, two, one, or rejected by all neurosurgeons, in experiment 5.

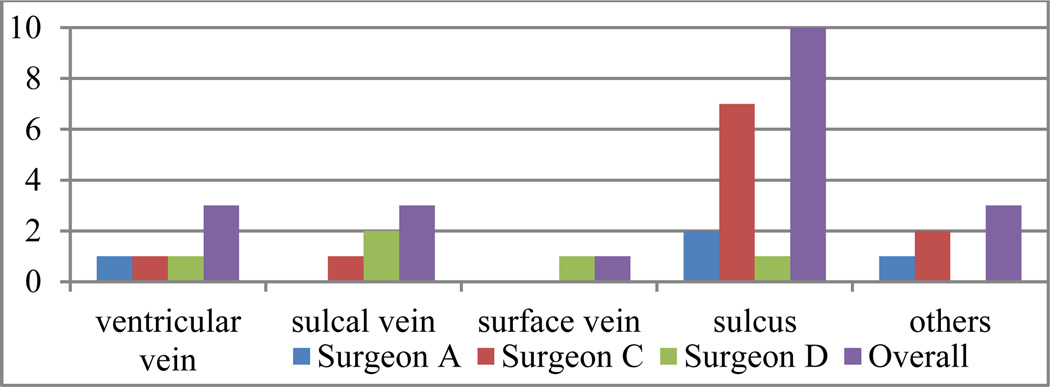
Fig. 10 shows the reasons for which the trajectories were rejected and the number of times each surgeon cited a particular reason. The cause for rejection is typically proximity to critical structures, including the sulci, veins/vessels around the ventricles (referred to as ventricular vein), veins/vessels around sulci (referred to as sulcal vein), and veins/vessels around the skull (it may either be in dural matter or in cortical zones, referred to as surface vein), or some other issues (too medial or too lateral). Trajectories rejected for multiple reasons were counted multiple times. As can be seen in the figure, the main reason for rejection is related to sulci.

Fig. 10.

Distributions of trajectories rejected by surgeons according to different rejection reasons in experiment 5.

For the trajectories that are rejected, we calculate the angle between the computed trajectories and the ones modified by the surgeons. The average value for this angle is 7.38° and its standard deviation is 6.23°.

V. DISCUSSION AND CONCLUSION

The selection of safe trajectories is an important component of DBS procedures and one that requires considerable expertise. In this article, we build on our own and the work of others to investigate whether or not computer-assistance would be valuable and whether or not systems need to be adapted for each surgeon to capture his/her preferences. Our institution is only one of a few in the US where two neurosurgeons perform DBS surgeries. Based on informal conversations with these surgeons, we started our study with the belief that different sets of weights would be necessary. Experiment 1 shows that our training mechanism, albeit heuristic, can capture surgeon preferences. The results we obtained with experiment 2 were unexpected and suggest that, in fact, the same set of weights could be used to compute trajectories for both surgeons at our institution. Experiment 3 shows that the clinical acceptance of automatic trajectories is comparable to the acceptance of trajectories manually selected by the other surgeon at our institution. Results obtained in experiment 4 show that when presented with only one trajectory and asked to rate it as acceptable or not as is the case in our pseudo-prospective study, surgeons are more selective than when comparing two trajectories without knowing their provenance as is the case in experiments 1 and 2. Indeed, most of the cases rejected pseudo-prospectively in experiment 4 were previously rated acceptable or better. The main difference between the pseudo-prospective and retrospective experiments is that in the former the surgeon knows unequivocally that the trajectory is computed. In the latter the trajectories’ provenance is unknown. Even though the reason for this difference could not be elucidated with our experiments, the fact that the surgeons were stricter in the pseudo-prospective situation only reinforces the value of the results we have obtained in experiment 5. This experiment is the largest we know of and the only one that has been conducted with neurosurgeons expert in DBS procedures at three different institutions. One surgeon has 17 years of experience with DBS procedures and has implanted more than 1140 leads, one has 16 years of experience and has implanted more than 1000 leads, one has 8 years of experience and has implanted more than 640 leads, and one has 4 years of experience and has implanted more than 122 leads. The results we have obtained with three of these surgeons and with 60 trajectories suggest that using a single set of weights may be adequate for multiple surgeons. The results also show that automatically computed trajectories were accepted 95% of the time by a majority of the neurosurgeons in our group and 76.67% unanimously. Acceptance rates by individual surgeons for these trajectories ranged between 83.33% and 95%, which indicate that computer-assisted assistance may be a valuable addition to DBS planning software. In our experience, eliciting priorities or even preferences from surgeons is not a straightforward task. For instance, one of the two surgeons at our institution mentioned that he likes to select trajectories that intersect the lateral edge of the thalamus (Rule 6). After training, the weight estimated for this rule for surgeon A was small. It ended up not being used in our pseudo-prospective study because surgeon B’s weights were used and he did not utilize this rule. As shown in our experiments, surgeon A ended up preferring the weights selected for surgeon B, suggesting, as discussed earlier, that surgeon A was not as critical as surgeon B during the training phase, thus further illustrating the difficulty of capturing surgeon preferences. This was also reported by Essert et al. [8] and Bériault et al. [9]. If larger studies performed at more sites confirm the fact that the same weights can be used across institutions, it may help standardize the procedure and assist surgeons who do not have years of experience with DBS procedures. Given enough training trajectories, an alternative would be to learn surgeon preferences algorithmically.

Constraints reported in the literature but not included in our model, such as minimizing the path length as done by Essert et al. [8] or the overlap with caudate as done by Bériault et al. [9], were not listed as reasons to reject a single trajectory. However, a recent study by Witt et al. [20] reports that trajectories that intersect with caudate nuclei may increase the risk of a decline in global cognition and memory performance; Benabid et al. [3] also suggest selecting trajectories that do not intersect the caudate. Other sites may thus have different preferences and several cost functions may have to be designed to reflect this variability, further suggesting the need for larger studies. We also note that our study focuses on STN targeting. We are now beginning to capture rules that are used for other targets such as ventrointermediate nucleus (VIM) and globus pallidus interna (GPi). We will then follow a procedure similar to the one described herein to determine whether or not automatic trajectory planning would also be useful for these targets.

As shown in Fig. 10, the main reason for trajectory rejection is the spatial proximity to the sulci. A close inspection of the rejected trajectories shows that these penetrated the brain at the top of a gyrus, as desired, but were too close to the bottom of a sulcus. Our current approach only detects an intersection with the cortical surface and tries to determine if this intersection happens in a sulcal or gyral area, but does not penalize trajectories that are close to a sulcus once they have penetrated a gyrus. We are currently addressing this issue by localizing sulci and computing distance maps from these. We will then modify our sulcus-related cost term accordingly. In the current study, we decouple the segmentation and the path computation components by validating the segmentation visually. About 20% of the volumes required some minor editing, e.g., displacement of the ventricular boundary or enlargement of ventricular veins. Our vessel segmentation method is simple but we have compared it to the technique proposed by Frangi et al. [21] and have obtained similar results. When available, additional MR volumes acquired with sequences such as susceptibility weighted imaging (SWI) or time-of-flight (TOF) MRI as proposed by Bériault et al. [9] would facilitate the segmentation of the vasculature.

Finally, integrating our solution in our clinical solution (CRAVE) [22] for a full prospective study still requires a few improvements. Here, the target point was known and fixed. In the system in place at Vanderbilt, targets are predicted automatically and optimal trajectories can be computed for these. But, when the plan is finalized by the surgeons, the target position may be modified, which may also invalidate the pre-computed trajectory and necessitate re-computation. We are currently investigating the sensitivity of the solution to the position of target point, which is rarely moved by more than 1.5 mm. If it is very sensitive to the target point, clinical implementation may require pre-computing a series of solutions or constraining the search space to produce new solutions in clinically acceptable time.

Ultimately, computer assistance should help the surgical team in selecting a safe trajectory. Precomputing an optimal solution and presenting it to the end user focuses him/her on what the system determines to be the safest entry point but the system also needs to permit easy interactive validation. Providing visual feedback in the form of segmented structures, risk values, distance to critical structures, or color-coded maps as others have done [4–10] and as shown in Fig. 3 and 4 would also assist the surgeons in selecting an alternative entry point that may not be in the immediate vicinity of the suggested one should it be rejected.

As implemented, extracting the cortical surface takes about 2 hours to compute, segmenting the other structures 10 minutes, pre-computing the sulci cost for every entry point in the search region 10 minutes, and computing an optimal trajectory once all the pre-computations have been done a few seconds.