Skip to main content
. Author manuscript; available in PMC: 2014 Aug 25.
Published in final edited form as: J Mol Biol. 1996 Jun 7;259(2):249–263. doi: 10.1006/jmbi.1996.0317

Figure 1.

Figure 1

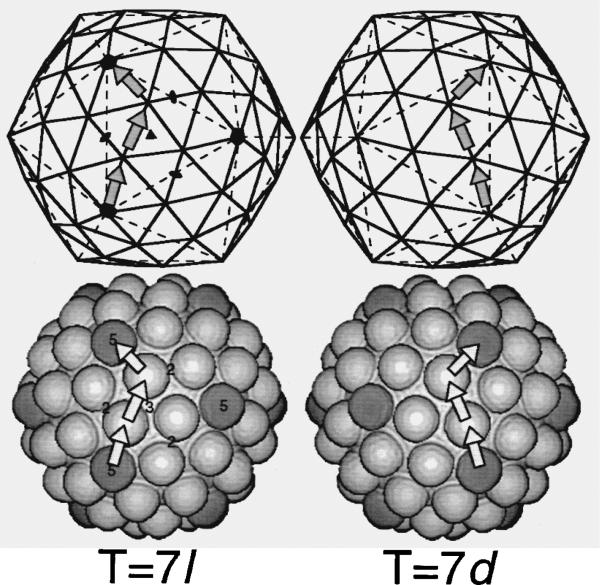
Icosahedra with a triangulation number of seven (T = 7) are left (T = 7laevo) or right (T = 7dextro) handed. Here, T = 7l and T = 7d lattices (top row, continuous lines) and computer-generated models (bottom row) are displayed. Vertices in the lattices are replaced by spheres in the models. For the papovaviruses, each sphere represents a pentameric capsomere. Three adjacent, 5-fold-symmetry axes (filled pentagons, top left) define the vertices of one of the 20 triangular faces in the basic, T = 1 icosahedron (broken lines, top row). Both 2-fold and 3-fold symmetry elements (filled ovals and triangle, respectively) are depicted also within this triangular face. (Filled symbols are replaced by numbers in the lower left figure.) A T = 7 lattice has 72 vertices or lattice points that define the corners of 140 smaller triangles. The 12 pentavalent vertices at the 5-fold axes are each surrounded by five hexavalent vertices, giving a total of 60 hexavalent lattice points (three in each face of the T = 1 lattice). Each hexavalent lattice point is surrounded by one pentavalent and five hexavalent points. Pentava-lent spheres in the computer models (bottom row) are shaded dark grey to distinguish them from hexavalent spheres. The absolute hand of a T = 7 lattice is defined by the arrangement of lattice points between neighboring pentavalent points, analogous to the moves a knight makes in the game of chess. Thus, in a T = 7l lattice (top left) or structure (bottom left) the path between adjacent pentavalent lattice points or capsomeres consists of two “steps” forward onto adjacent hexavalent points followed by one step to the left (arrows). Similarly, a T = 7d lattice (top right) or structure (bottom right) exhibits a “two steps forward followed by one to the right” pattern. The lattices and computer models are enantiomorphs (i.e. mirror related). However, if all spheres in each model were replaced by chemically identical, chiral, pentameric capsomeres as are found in all papovaviruses, the resulting T = 7l and T = 7d structures would not be an enantiomorphic pair.