Two-axis control of a singlet–triplet qubit with an integrated micromagnet

Significance

Qubits, the quantum-mechanical analog of classical bits, are the fundamental building blocks of quantum computers, which have the potential to solve some problems that are intractable using classical computation. This paper reports the fabrication and operation of a qubit in a double-quantum dot in a silicon/silicon–germanium (Si/SiGe) heterostructure in which the qubit states are singlet and triplet states of two electrons. The significant advance over previous work is that a proximal micromagnet is used to create a large local magnetic field difference between the two sides of the quantum dot, which increases the manipulability significantly without introducing measurable noise.

Abstract

The qubit is the fundamental building block of a quantum computer. We fabricate a qubit in a silicon double-quantum dot with an integrated micromagnet in which the qubit basis states are the singlet state and the spin-zero triplet state of two electrons. Because of the micromagnet, the magnetic field difference ΔB between the two sides of the double dot is large enough to enable the achievement of coherent rotation of the qubit’s Bloch vector around two different axes of the Bloch sphere. By measuring the decay of the quantum oscillations, the inhomogeneous spin coherence time ${\mathit{T}}_{\mathbf{2}}^{\text{*}}$ is determined. By measuring ${\mathit{T}}_{\mathbf{2}}^{\text{*}}$ at many different values of the exchange coupling J and at two different values of ΔB, we provide evidence that the micromagnet does not limit decoherence, with the dominant limits on ${\mathit{T}}_{\mathbf{2}}^{\text{*}}$ arising from charge noise and from coupling to nuclear spins.

Fabricating qubits composed of electrons in semiconductor quantum dots is a promising approach for the development of a large-scale quantum computer because of the approach’s potential for scalability and for integrability with classical electronics. Much recent progress has been made, and spin manipulation has been demonstrated in systems of two (1–5), three (6, 7), and four (8) quantum dots. A great deal of attention has focused on the singlet–triplet qubit in quantum dots (1, 2, 9–18), which consists of the S_z = 0 subspace of two electrons, for which the basis can be chosen to be a singlet and a triplet state. Full two-axis control on the Bloch sphere is achieved by electrical gating in the presence of a magnetic field difference ΔB between the two dots. In previous experiments (2, 9–14), ΔB arises from coupling to nuclear spins in the material, and slow fluctuations in these nuclear fields lead to inhomogeneous decoherence times that, without special nuclear state preparation, typically are shorter than the period of the quantum oscillations. In III–V materials, ΔB is large, so fast oscillation periods of order 10 ns are achievable, but the inhomogeneous dephasing time is also ∼10 ns, so that oscillations from ΔB are overdamped, ending before a complete cycle is observed (2). The fluctuations of the nuclear spin bath can be mitigated to some extent (10), but inhomogeneous dephasing times in III–V materials are short enough that high-fidelity control is still very challenging. Coupling to nuclear spins in silicon is substantially weaker, leading to longer coherence times, but also smaller field differences and hence slower quantum oscillations (14, 19).

Here, we report the operation of a singlet–triplet qubit in which the magnetic field difference ΔB between the dots is imposed by an external micromagnet (20, 21). Because the field from the micromagnet is stable in time, a large ΔB can be imposed without creating inhomogeneous dephasing. We present data demonstrating underdamped quantum oscillations, and, by investigating a variety of voltage configurations and two ΔB configurations, we show that the micromagnet indeed increases ΔB without significantly increasing inhomogeneous dephasing rates induced by coupling to nuclear spins.

A top view of the double-quantum dot device, which is fabricated in a Si/SiGe heterostructure, is shown in Fig. 1A; fabrication techniques are discussed in Materials and Methods, and an optical image of the micromagnet can be found in SI Appendix. The charge occupation of the two sides of the double dot is determined by measuring the current through a quantum point contact (QPC) next to one of the dots, as shown in Fig. 1A. Fig. 1B shows a charge stability diagram, obtained by measuring the current through the QPC as a function of gate voltages on the left plunger (LP) and right plunger (RP); the number of electrons on each side of the dot is labeled. The qubit manipulations are performed in the (1, 1) region (detuning ε > 0), and initialization and readout are carried out in the (0, 2) region (ε < 0). Fig. 1C shows the energy-level diagram at small but nonzero magnetic field. The three triplet states T₋ = |↓↓〉, $T_0=\left(|\uparrow \downarrow \rangle +|\downarrow \uparrow \rangle \right)/\sqrt{2}$, and T₊ = |↑↑〉 are split from each other by the Zeeman energy E_Z = gμ_BB_ave, where g is the gyromagnetic ratio, μ_B is the Bohr magneton, and B_ave is the average of the total magnetic field. A difference in the transverse magnetic fields on the dots, either from the external micromagnet or from nuclear hyperfine fields, mixes the singlet S and triplet T₋ states and turns the S-T₋ crossing into an anticrossing. This avoided crossing enables the observation of a spin funnel where the S-T₋ mixing is fast (2) as well as quantum oscillations between S and T₋ (22). The spin funnel is shown in Fig. 1E, and the S-T₋ oscillations are shown in Fig. 1 F and G. The applied pulse in Fig. 1E is a simple one-stage pulse along the detuning direction with fixed amplitude (shown in Fig. 1C, Inset), repeated at a rate of 33 kHz, which is slow enough for spin relaxation to reinitialize to the singlet before application of the next pulse (23, 24). The lever arm α, the conversion between detuning energy ε and gate voltage V_ε, is 35.4 μeV/mV. See SI Appendix for methods used to extract α and convert the measured QPC current to the probability of being in the S state at the end of the applied pulse. The spin funnel is obtained by sweeping along the detuning direction (i.e., sweeping V_ε) with the pulse on, and stepping the external magnetic field B_ext. When the pulse tip reaches the S-T₋ anticrossing, a strong resonance signal is observed, corresponding to strong mixing of S-T₋ states. Because right at the anticrossing E_Z ≃ J, we can map out J at small ε by sweeping the magnetic field. The center of the spin funnel occurs when the applied field cancels out the average field from the micromagnet, which indicates B_ave ≃ 2.5 mT. The tunnel coupling t_c ∼ 3.4 μeV is estimated from the dependence of the location of the spin funnel on magnetic field (2). The pulse rise time of 10 ns ensures nearly adiabatic passage over the S(0, 2) to S(1, 1) anticrossing, with a nonadiabatic transition probability <0.1% (25).

Fig. 1.

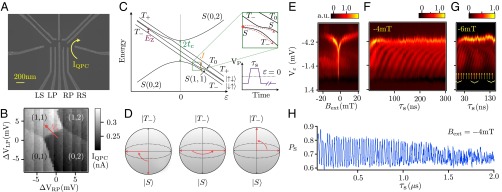
(A) Scanning electron micrograph of a device identical to the one used in the experiment before deposition of the gate dielectric and accumulation gates. An optical image of a complete device showing the micromagnet is included in SI Appendix. Gates labeled left side (LS) and right side (RS) are used for fast pulsing. The curved arrow shows the current path through the QPC used as a charge sensor. (B) I_QPC measured as a function of V_LP and V_RP yields the double-dot charge stability diagram. Electron numbers in the left and right dot are indicated on the diagram. The red arrow denotes the direction in gate voltage space $V_{\epsilon }=\sqrt{\mathrm{\Delta }{V}_{LP}^2+\mathrm{\Delta }{V}_{RP}^2}$ that changes the detuning ε between the quantum dots. (C) Schematic energy diagram near the (0, 2) to (1, 1) charge transition, showing energies of singlet S and triplet T states as functions of ε. The exchange energy splitting J between S and T₀, the Zeeman splitting E_Z between T₋ and T₀, and the tunnel coupling t_c are also shown. At large ε, in the presence of a field difference between the two dots, S and T₀ mix, and the corresponding energy eigenstates are |↑↓〉 and |↓↑〉. At small ε, the small transverse field from the micromagnet and the nuclear fields turns the S-T₋ crossing into an anticrossing (zoom in). Pulsing through this anticrossing with intermediate velocity transforms S into a superposition of S and T₋, leading to Landau–Stückelberg–Zener oscillations at the frequency corresponding to the S-T₋ energy difference (22). The pulse used to observe the spin funnel and S-T₋ oscillations shown in E is also shown, where the pulse voltage V_P is applied along the detuning axis. (D) Bloch sphere representation of π rotation of S and T₋ states with 50% initialization into each state. (E) Spin funnel (2) measurement of the location of the S-T₋ anticrossing as a function of external magnetic field B_ext and V_ε. The data were acquired by sweeping along the detuning direction with the pulse on, with the vertical axis reporting the value of the detuning at the base of the pulse. The spin funnel occurs when S-T₋ mixing is fast, which locates the relevant anticrossing. (F and G) S-T₋ oscillations acquired at different external B fields. The oscillation frequency increases with increasing B_ext. The slower oscillations in G with period ∼80 ns and labeled with the curly brackets are S-T₀ oscillations, which are investigated in more detail in Figs. 2 and 3. The S-T₋ oscillations in G are labeled with arrows. (H) Singlet probability as a function of pulse duration τ_s at external magnetic field B = −4 mT and base detuning V_ε ≃ −2.8 mV.

By increasing the rise time of the pulse, so that it is slower than that used to observe the spin funnel, the voltage pulse can be used to cause S to evolve into a superposition of the S and T₋ states. In this case, the pulse remains adiabatic with respect to the S(0, 2)–S(1, 1) anticrossing; it is, however, only quasi-adiabatic with respect to the S-T₋ anticrossing, enabling use of the Landau–Zener mechanism to initialize a superposition between states S and T₋ (Fig. 1C, Inset) (22, 26–28). Because the voltage pulse takes these states to larger detuning, an energy difference arises between the pair of states, and there is a relative phase accumulation between them. The return pulse leads to quantum interference between these two states and to oscillations in the charge occupation as a function of the acquired phase. Fig. 1D illustrates the ideal case, in which the rising edge of the pulse transforms S into an equal superposition of S and T₋, followed by accumulation of a relative phase difference of π after pulse duration τ_S. Fig. 1F shows S-T₋ oscillations at B_ext = −4 mT, obtained by applying a pulse with a rise time of 45 ns. Fig. 1H reports a line scan of the singlet probability for S-T₋ oscillations measured at B_ext = −4 mT; for this measurement, the tip of the voltage pulse reaches large enough detuning that $E_{S{T}_{-}}$ is essentially constant and independent of detuning. From this data we extract a dephasing time of 1.7 μs by fitting the oscillation amplitude to a Gaussian decay function of the pulse duration τ_S. The S-T₋ oscillations observed here are longer-lived than those observed in GaAs (22), presumably in part because Si has weaker hyperfine fields (29). However, the visibility here is similar to that in GaAs, indicating that decoherence is still important in limiting the ability to tune the pulse rise time to achieve equal amplitude in the S and T₋ branches of the Landau–Zener beam splitter (22, 26–28). Fig. 1G shows a similar measurement for which we used a slightly faster (16 ns) rise time for the pulse, the effect of which is to increase the overlap of the wavefunction with the singlet state S; as a result, both S-T₋ oscillations and S-T₀ oscillations are visible in this plot, which was acquired at B_ext = −6 mT. The faster oscillations with period 10 ns, marked with the small arrows in Fig. 1G, are the S-T₋ oscillations. The slower oscillations, marked with the curly brackets, are the S-T₀ oscillations. As we discuss below, these latter oscillations can be made dominant by further modifications of the manipulation pulse, and for these oscillations the micromagnet plays a critical role in enhancing the rotation rate on the S-T₀ Bloch sphere.

We investigate the S-T₀ oscillations, which correspond to a gate rotation of the S-T₀ qubit, in more detail by changing the applied magnetic field B_ext to −30 mT, and by working with faster pulse rise times. Here the S-T₋ anticrossing occurs at negative ε, as shown in Fig. 2A, making it easier to pulse through that anticrossing quickly enough so that the state remains S. In this situation, the relevant Hamiltonian H for ε > 0, in the S-T₀ basis, is

$$H=\left[\begin{array}{cc}-J\left(\mathit{ϵ}\right)& h/2\\ h/2& 0\end{array}\right].$$ [1]

Here, J is the exchange coupling and h = gμ_BΔB is the energy contribution from the magnetic field difference. The angle θ between the rotation axis and the z axis of the Bloch sphere satisfies tanθ = h/J, and the rotation angular frequency $\omega =\sqrt{h^2+J^2}/\mathit{\hslash }$. Both θ and ω depend on ε, because J varies with ε.

Fig. 2.

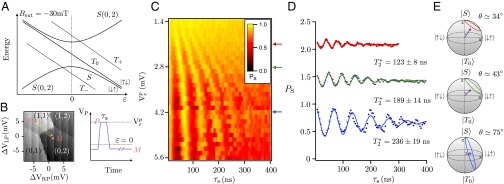
(A) Schematic energy level diagram near the (0, 2)–(1, 1) charge transition at external field B_ext = −30 mT. (B) Pulse sequence used to observe S-T₀ oscillations. Starting at point M in the S(0, 2) ground state, a fast adiabatic pulse into (1, 1) is applied [it is adiabatic for the S(0, 2)–S(1, 1) anticrossing and sudden for the S(1, 1)-T₀ anticrossing], to point P, where the exchange coupling J is comparable to or less than h, the energy from the magnetic field difference. The speed and axis of the rotation on the Bloch sphere during the pulse of duration τ_S depend on both J and h. Readout is performed by reversing the fast adiabatic pulse, which converts S(1, 1) to S(0, 2) but does not change the charge configuration of T₀. (C) Probability P_S of being in state S as a function of the detuning voltage at the pulse tip, $V_{\epsilon }^{\text{p}}$, and the pulse duration τ_s. Here, the measurement point M in the (0, 2) charge state is fixed while $V_{\epsilon }^{\text{p}}$ and τ_s are varied. (D) P_S as a function of τ_s, extracted from the data in C at three different values of V_ε. Each trace is fit to the product of a cosine and a Gaussian (30, 31), with amplitude, frequency, phase, and decay time as free parameters (solid curves). The decay time ${\mathit{T}}_{\mathrm{2}}^{\text{*}}$ is listed for each trace. Each trace is offset by 0.6 for clarity. (E) Bloch spheres showing the rotations corresponding to each trace in D. The angle θ between the rotation axis and the z axis is labeled for each case.

Rotations around the x axis of the Bloch sphere (the “ΔB gate”) are implemented using the simple one stage pulse shown in Fig. 2B, starting from point M in the (0, 2) charge state. The pulse rise time of a few nanoseconds is slow enough that the pulse is adiabatic through the S(0, 2) to S(1, 1) anticrossing. As ε increases, the eigenstates transition from S(1, 1) and T₀ to other combinations of |↑↓〉 and |↓↑〉, and in the limit of ε → ∞, the eigenstates become |↑↓〉 and |↓↑〉. The voltage pulse applied is sudden with respect to this transition in the energy eigenstates, so that immediately following the rising edge of the pulse the system remains in S(1, 1). At large detuning, J ≤ h, and S-T₀ oscillations are observed following the returning edge of the pulse. These oscillations arise from the x component of the rotation axis and have a rotation rate that is largely determined by the magnitude of h. Fig. 2C shows the singlet probability P_S plotted as a function of the detuning voltage at the pulse tip, $V_{\epsilon }^{\text{p}}$, and pulse duration τ_S. The data in the top one-third of the figure were acquired with a pulse rise time of 2.5 ns, and the data shown in the bottom two-thirds of the figure were acquired using a 5-ns rise time. As is clear from Fig. 2 C and D, J decreases as ε increases, so the oscillation angular frequency becomes smaller and approaches h/ℏ as J → 0. The visibility of the oscillations is largest at large $V_{\epsilon }^{\text{p}}$, because in that regime the rotation axis is closest to the x axis, as shown in Fig. 2E. By fitting traces from Fig. 2C to the product of a cosine and a Gaussian (30), we extract the inhomogeneous dephasing time ${\mathit{T}}_{\mathrm{2}}^{\text{*}}$ as a function of ε. Based on the rotation period at large ε, we estimate h ∼ 60.5 neV, which corresponds to an X-rotation rate of 14 MHz. The rotation rate we observe here is much faster than the X-rotation rate achievable without micromagnets in Si, which is ∼460 kHz (14); micromagnets closer to the quantum dots offer the potential for even faster rotation rates than those reported here. Using feedback to prepare the nuclear spins in GaAs quantum dots, X-rotation rates of 30 MHz have been reported (18), comparable but slightly faster than the rates we achieve here without such preparation.

Fig. 3 shows oscillations around the z axis of the Bloch sphere, obtained by applying the exchange pulse sequence pioneered in (2). Starting from point M in S(0, 2), we first ramp from M to N at a rate that ensures fast passage through the S(0, 2)-T₋ anticrossing, converting the state to S(1, 1), and then ramp adiabatically from N to P, which initializes to the ground state in the J < h region. The pulse from P to E increases J suddenly so that it is comparable to or bigger than h, so that the rotation axis is close to the z axis of the Bloch sphere. Readout is performed by reversing the ramps, which projects |↓↑〉 into the S(2, 0) state, enabling readout. Fig. 3C shows the singlet probability P_S as a function of τ_S and the detuning of the exchange pulse $V_{\epsilon }^{\text{ex}}$ (point E in Fig. 3B) in a range of ε where J ≳ h. As $V_{\epsilon }^{\text{ex}}$ decreases, the oscillation frequency increases, because J is increasing. The oscillation visibility also increases as the rotation axis moves toward the z axis, as shown in Fig. 3 D and E. The inhomogeneous dephasing time ${\mathit{T}}_{\mathrm{2}}^{\text{*}}$, extracted by fitting the time dependence of P_S in Fig. 3D to the product of a Gaussian and a cosine function, decreases as J increases, which we argue is evidence that charge noise is limiting coherence in this regime (see below and Fig. 4).

Fig. 3.

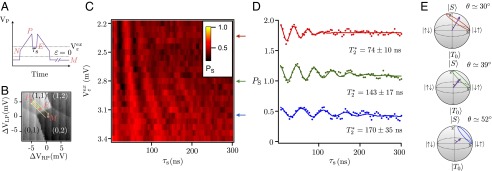
(A and B) Pulse sequence used to observe S-T₀ oscillations when J > h. We initialize into the S(1, 1) state by preparing the S(0, 2) ground state at point M and ramping adiabatically through the (0, 2)–(1, 1)S anticrossing to an intermediate point N and then to P, where the singlet and triplet states are no longer energy eigenstates. Decreasing ε suddenly brings the state nonadiabatically to a value of the detuning where J is comparable or greater than h, inducing coherent rotations. The Bloch vector rotates around the new axis for a time τ_s. Reversing the sequence of ramps projects the state into S(0, 2) for readout. (C) Probability P_S of observing the singlet as a function of the detuning voltage of the exchange pulse $V_{\epsilon }^{\text{ex}}$ and pulse duration τ_s with the measurement point M fixed in the (0, 2) charge state. (D) P_S as a function of τ_s, extracted from the data in C at three different values of $V_{\epsilon }^{\text{ex}}$. Each trace is offset by 0.7 for clarity. Solid curves are fits to the product of a cosine and a Gaussian (30), with amplitude, frequency, phase, and decay time as free parameters. (E) Bloch spheres showing rotations around the axes corresponding to each trace in D. The angle θ between the rotation axis and the z axis is labeled for each case.

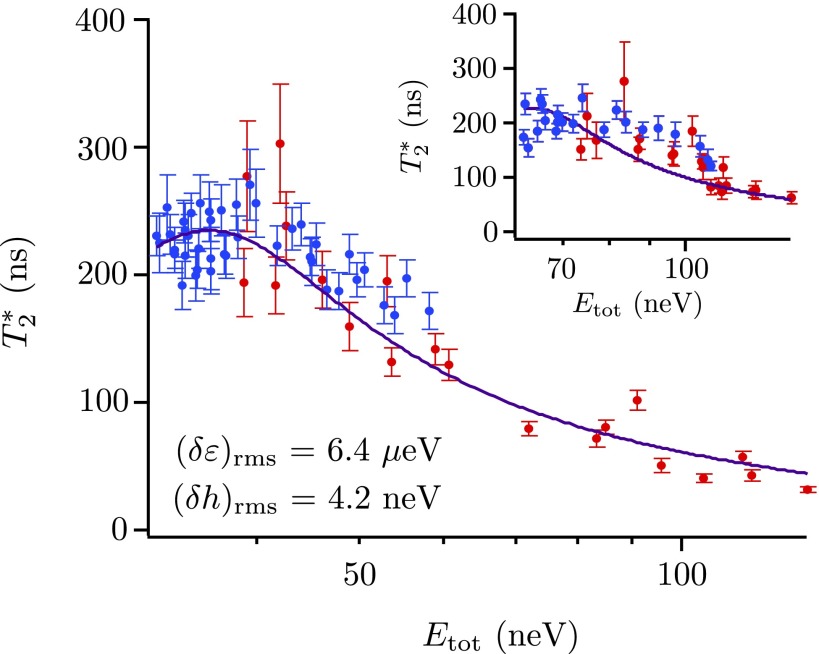
Fig. 4.

Dependence of the inhomogeneous dephasing time ${\mathit{T}}_{\mathrm{2}}^{\text{*}}$ on rotation energy $E_{\mathrm{t}\mathrm{o}\mathrm{t}}=\sqrt{J^2+h^2}$, where J is the exchange coupling and h is the energy corresponding to the magnetic field difference between the dots. (Inset) Plot of the extracted values of ${\mathit{T}}_{\mathrm{2}}^{\text{*}}$ for h ≃ 60.5 neV. Red data points are ${\mathit{T}}_{\mathrm{2}}^{\text{*}}$ values obtained using the exchange pulse sequence (Fig. 3), and blue data points are ${\mathit{T}}_{\mathrm{2}}^{\text{*}}$ values obtained using the ΔB pulse (Fig. 2). Main panel: ${\mathit{T}}_{\mathrm{2}}^{\text{*}}$ plotted vs. E_tot for h ≃ 32 neV, extracted from data shown in SI Appendix, Fig. S3. Red data points are obtained using the exchange pulse sequence (SI Appendix, Fig. S3B), and blue data points are obtained using the ΔB pulse (SI Appendix, Fig. S3A). The solid lines in the main panel and in Inset are plots of Eq. 2 with the same values of δε, the rms fluctuation in the detuning, and δh, the rms fluctuation of the magnetic field difference, which were obtained by fitting the data for ${\mathit{T}}_{\mathrm{2}}^{\text{*}}$ as function of E_tot at h ≃ 32 neV to Eq. 2. The good agreement of the same form with both data sets is strong evidence that the inhomogeneous dephasing is dominated by charge noise and hyperfine fields and does not depend on the magnetization of the micromagnet.

We also implemented both the ΔB and exchange gate sequences after performing a different cycling of the external magnetic field, which resulted in a different value of ΔB, corresponding to h ≃ 32 neV. The results obtained are qualitatively consistent with those shown in Figs. 2 and 3 (data shown in the SI Appendix, Fig. S3).

We now present evidence that the inhomogeneous dephasing is dominated by detuning noise and by fluctuating nuclear fields, and that it does not depend on the field from the micromagnet. Following ref. 18, we write $1/{\mathit{T}}_{\mathrm{2}}^{\text{*}}=\sqrt{\langle {\left(\delta E_{\text{tot}}\right)}^2\rangle }/\left(\sqrt{2}\mathit{\hslash }\right)$, where δE_tot = δJ(∂E_tot/∂J) + δh(∂E_tot/∂h), with δE_tot the fluctuation in E_tot, δJ the fluctuation in J, and δh the fluctuation in h. We assume that the fluctuations in h and J are uncorrelated. If fluctuations in J are dominated by fluctuations in the detuning, δε, then δJ ∼ δε(dJ/dε), and if fluctuations in h are dominated by nuclear fields, then δh is independent of ε, leading to

$$\sqrt{2}\hslash T_2^{\text{*}-1}={\left({\left(\frac{J}{E_{\text{tot}}}\frac{dJ}{d\epsilon }\delta {\epsilon }_{\text{rms}}\right)}^2+{\left(\frac{h}{E_{\text{tot}}}\delta h_{\text{rms}}\right)}^2\right)}^{\frac{1}{2}},$$ [2]

with δε_rms and δh_rms both independent of E_tot as well as h. We use the measured E_tot vs. ε to extract J(ε), which is well-described by an exponential, J(ε) ≃ J₀exp(−ε/ε₀), consistent with ref. 18 in the same regime (SI Appendix). In Fig. 4 we fit ${\mathit{T}}_{\mathrm{2}}^{\text{*}}$ using the experimentally determined dJ/dε, the measured E_tot, and constant values δε_rms = 6.4 ± 0.1 μeV and δh_rms = 4.2 ± 0.1 neV. The fit is good, and the values of δε_rms and δh_rms agree well with previous reports of charge noise and fluctuations in the nuclear field in similar devices and materials (14, 29, 30, 32–34). Fig. 4 Inset, which shows data obtained at a larger h, demonstrates that ${\mathit{T}}_{\mathrm{2}}^{\text{*}}$ is well-described by Eq. 2 with the same δε_rms and δh_rms, providing evidence that changing the magnetization of the micromagnet does not significantly affect the qubit decoherence. Eq. 2 and Fig. 4 also make it clear that ${\mathit{T}}_{\mathrm{2}}^{\text{*}}$ is larger for larger detunings, because charge noise has much less effect away from the primary anticrossing.

In summary, we have demonstrated coherent rotations of the quantum state of a singlet–triplet qubit around two different directions of the Bloch sphere. Measurements of the inhomogeneous dephasing time at a variety of exchange couplings and two different field differences demonstrate that using an external micromagnet yields a large increase in the rotation rate around one axis on the Bloch sphere without inducing significant decoherence. Because the materials fabrication techniques are similar for both quantum dot-based qubits and donor-based qubits in semiconductors (35), it is reasonable to expect micromagnets also should be applicable to donor-based spin qubits (36–38). Micromagnets allow a difference in magnetic field to be generated between pairs of dots that does not depend on nuclear spins, and thus offer a promising path toward fast manipulation in materials with small concentrations of nuclear spins, including both natural Si and isotopically enriched ²⁸Si.

Materials and Methods

All measurements reported in this manuscript were made on a double-quantum dot device fabricated in an undoped Si/Si_0.72Ge_0.28 heterostructure with a 12-nm-thick Si quantum well located 32 nm below the heterostructure surface. The double-quantum dot is defined using two layers of electrostatic gates (39–44). The lower layer of depletion gates is shown in Fig. 1A. The upper and lower layer of gates are separated by 80 nm of Al₂O₃ deposited via atomic layer deposition. The upper layer of gates is positively biased to accumulate a 2D electron gas in the Si well. The micromagnet, a rectangular thin film of cobalt, is deposited via electron-beam evaporation on top of the gate structure, 1.78 μm from the double-dot region (SI Appendix). A uniform in-plane magnetic field B_ext is applied, and cycling B_ext to relatively large values is used to change the magnetization of the micromagnet. All measurements were made in a dilution refrigerator with an electron temperature of ∼120 mK, as determined using the method of ref. 45.