Significance
Influenza hemagglutinin (HA), a viral surface glycoprotein, undergoes a critical and large conformational rearrangement to promote fusion of the viral membrane with the host membrane. Unlike the variable receptor binding domain HA1, the coiled-coil domain HA2 is highly conserved, making HA2 a promising target for therapeutics. Furthermore, the structural similarity between influenza HA2 and other viral fusion proteins, including that of HIV, makes HA2 a valuable model system. We build a model using information from only the prefusion and postfusion configurations of HA2 and use molecular dynamics simulations to characterize the structural ensembles found during the conformational transition. We find that local unfolding facilitates interaction of HA2 with the host membrane and enables a quasi-stable asymmetric intermediate during the transition.
Keywords: protein folding, structure-based model
Abstract
Influenza hemagglutinin (HA), a homotrimeric glycoprotein crucial for membrane fusion, undergoes a large-scale structural rearrangement during viral invasion. X-ray crystallography has shown that the pre- and postfusion configurations of HA2, the membrane-fusion subunit of HA, have disparate secondary, tertiary, and quaternary structures, where some regions are displaced by more than 100 Å. To explore structural dynamics during the conformational transition, we studied simulations of a minimally frustrated model based on energy landscape theory. The model combines structural information from both the pre- and postfusion crystallographic configurations of HA2. Rather than a downhill drive toward formation of the central coiled-coil, we discovered an order-disorder transition early in the conformational change as the mechanism for the release of the fusion peptides from their burial sites in the prefusion crystal structure. This disorder quickly leads to a metastable intermediate with a broken threefold symmetry. Finally, kinetic competition between the formation of the extended coiled-coil and C-terminal melting results in two routes from this intermediate to the postfusion structure. Our study reiterates the roles that cracking and disorder can play in functional molecular motions, in contrast to the downhill mechanical interpretations of the “spring-loaded” model proposed for the HA2 conformational transition.
Hemagglutinin (HA) is a viral receptor-binding and membrane-fusion glycoprotein involved in the invasion of influenza virions into host cells (1). Structural rearrangements of HA during membrane fusion are crucial for the delivery of the viral genome. The postfusion conformation of HA shows considerable similarity to other viral fusion proteins and eukaryotic membrane receptors involved in intracellular vesicle trafficking (2), suggesting there may be common mechanisms in the function of these proteins. Therefore, HA may serve as a model system, allowing characterization of the molecular and energetic details that underlie its conformational transition to provide insights into general principles of membrane fusion (3).
HA is a homotrimer consisting of two domains connected by disulfide bonds (4): a globular receptor binding domain (HA1), and a coiled-coil membrane-fusion domain anchored to the viral membrane (HA2). Recognized by the sialic acid receptor of a host cell, the intact virus enters the cell via endocytosis. Low pH in a late endosome then induces the dissociation of HA1 from HA2 (1) and an irreversible conformational transition of HA2. Experimentally, this conformational change can be triggered by either low pH, high temperature, or urea denaturation (5).
Structures of HA in pre- and postfusion pH conformations have been solved by X-ray crystallography. The structure of the prefusion ectodomain contains both HA1 and HA2, and was purified from influenza virions (4). A postfusion conformation of HA1 and HA2 were obtained from prefusion viral HA that was sequentially treated with low pH and trypsin (6, 7). Comparison of these two structures shows no structural changes in HA1, but a major rearrangement in HA2, including secondary, tertiary, and quaternary structural changes. The N-terminal domain of HA2, initially adjacent to the transmembrane region in the prefusion configuration, undergoes a large movement (over 100 Å) during the transition. The C-terminal domain of HA2 changes from a globular structure to three extended loops packed against the central coiled-coil.
Although experiments have probed the fusion mechanism through mutation (8) and provided measures of fusion kinetics (9), there is a lack of structural information about how HA2 transitions from the prefusion to postfusion conformations. Theoretical models have been suggested to describe the fusion mechanism based on the available experimental kinetic data (10–12). However, because of the large scale of the HA2 rearrangement, only limited computational techniques, such as targeted molecular dynamics (13), have been applied to study the molecular details of the transition.
In this study we applied the principles of the energy landscape theory as developed in the context of protein folding (14–16) to examine structural details of the HA2 conformational transition. We used a structure-based model (SBM) (17, 18) built with a dual-funneled landscape (19, 20) that has both the pre- and postfusion structures as explicit minima. The HA2 landscape has at least two competing basins of attraction, corresponding to the pre- and postfusion structures of HA2, respectively. HA1 dissociation sterically enables HA2 to explore beyond the prefusion local free-energy minimum and to diffuse toward the postfusion configuration. The long-length scale and extensive shuffling of secondary and tertiary structures is reminiscent of protein folding, but distinct in that both ends of the HA2 transition can be described by ensembles of structurally similar configurations. Just as in protein folding, there may be free-energy barriers and structural intermediates along the HA2 transition caused by the imperfect cancellation of energy and entropy. These intermediate ensembles may be interesting candidates for drug design to inhibit HA function.
Previously, a “spring-loaded” model has been applied to describe the mechanism for the HA2 transition (21). This model suggested a downhill mechanical transition of the N-terminal region of HA2 into an ordered helical structure that orients the fusion peptides away from the virus and toward the host membrane. Our simulations expand this view by showing that the conformational change of the N-terminal domains is associated with an entropic barrier and the unfolding of the C-terminal region is associated with the major energetic barrier during the HA2 conformational transition. Kinetic competition between these two events creates a long-lived metastable intermediate that allows for two dominant routes. The first route (the “sequential route”) resembles the spring-loaded model, and the second route (the “cooperative route”) involves cooperative interactions between the N-terminal and C-terminal domains in forming the central coiled-coil. The presence of these distinct routes suggests multiple mechanisms for HA2 rearrangement and membrane fusion.
Results
Subscripts I and F are used to denote either the prefusion (I, initial) or the postfusion (F, final) basin. For example, the prefusion and postfusion states of the full HA2 trimer are denoted HA2I and HA2F throughout this paper, with similar notations being given to individual protein domains SI and SF. The HA2 trimer is partitioned into five segments, S1 to S5 (Fig. 1), identified from these crystal structures as regions with distinct structural changes during the transition (6, 22). We also highlight Loop3-4, a subset of S4 that becomes a loop connecting S3 and S4 in the postfusion structure. S1 (residues 33–56 in each monomer) undergoes rearrangement of tertiary structure, which brings the fusion peptides (not represented in the simulation) away from the viral membrane. S2 (residues 57–74 in each monomer) has both secondary and tertiary changes, transitioning from extended loops to α-helices. S3 (residues 75–106 in each monomer), a triple-stranded coiled-coil, is the only region that is structurally conserved between the HA2I and HA2F crystal structures. S4 (residues 107–127 in each monomer) partially reorganizes to orient itself antiparallel to the central coiled-coil S3. Loop3-4 (residues 107–112 in each monomer) undergoes a helix-to-coil transition. S5 (residues 128–175 in each monomer), an initially globular region near the viral membrane, breaks into three loops that pack into the grooves of the central helices in the HA2F configuration. Because of the trimeric nature of HA, the rearrangement also changes the quaternary structure of several sections. For example, S5 transitions from a configuration with many S5-S5 quaternary interactions in HA2I to a configuration with none in HA2F. The fusion peptides and their linkers to S1 (residues 1–32 in each monomer) initially have their N-termini buried in a cavity surrounded by S4. These residues do not exist in the postfusion structure, nor in our simulations.
Fig. 1.
Influenza hemagglutinin X-ray crystal structures. (Left) Receptor binding domain HA1 and membrane fusion domain HA2 oriented with respect to a cartoon membrane. A pH drop after endocytosis dissociates HA1 from the HA2 trimer, sterically allowing the conformational transition. (Right) The crystal structures of prefusion and postfusion HA2 (PDB IDs 2HMG and 1QU1) sectioned and colored by different regions from S1 to S5 (defined in the text). Open and filled circles denote the N and C termini, respectively.
In the case of protein folding, the number of atom pairs that form native contacts Q is often used as a reaction coordinate to characterize the folding dynamics (23, 24). Here, an atom pair was considered to be in contact if the pair existed as a native contact in one of the two crystal structures and the spatial distance between the atoms was less than 1.5 times their distance in the crystal structure (17). The reaction coordinate QX/Y was introduced to quantify the number of interface contacts between section X and Y. Because contacts unique to one conformation could be broken without a compensating contact unique to the other formed, the Q for either HA2F or HA2I individually cannot serve as a reaction coordinate to monitor the overall transition progress. Rather, we chose a difference of Q between HA2F and HA2I configurations: ΔQX/Y = QX/Y(HA2F) − QX/Y(HA2I), where Q(x) means Q relative to structure x. Accordingly, three reaction coordinates were selected: ΔQS123/S45 quantifies the number of interfacial contacts between subunits S1-3 and S4-5 and is a measure of global progression of the transition, whereas ΔQS1/S1 and ΔQS5/S5 measure both interfacial and intramonomer contacts within S1 and S5 and serve to distinguish between the two major routes observed in this transition. Finally, ΔQtrans = ΔQS123/S45 + ΔQS1/S1 was used to avoid a spurious backtracking along the coordinate ΔQS123/S45 (SI Appendix). All reaction coordinates were normalized to range from 0 to 1 (Fig. 2).
Fig. 2.
Two-dimensional kinetic probability distribution of the HA2 structural transition at T = 0.8Tm, the melting temperature of HA2 (Top). ΔQtrans = QS123–S45 + QS1–S1, ΔQS1–S1, and ΔQS5–S5 are used as the reaction coordinates and combine data from 1,000 independent trajectories. The deepest local minima are labeled as basins A–H and representative structures for each are shown below. (A) Thermal fluctuations about the HA2I crystal structure. (B) Arms (S1-2) of HA2 come off and fusion peptides are exposed. (C) HA2 bends resulting in a broken trimeric symmetry. (D and E) Same as B and C except that two helices in S1 have associated with each other. (F) All three helices in S1 associated. Note that by the time all three helices in S1 associate, HA has already bent in over 99% of the simulations, so the basin to the left of F is scarcely populated. (G) An intermediate state where the overall structural transition is complete except for one unit of S5, which is likely caused by asymmetry in the HA2F crystal structure. (H) Thermal fluctuations around the HA2F structure. Basins A–E represent the common “fast phase,” and the bifurcation from basin E distinguishes two transition routes. The Inset shows complete sampling for a single-basin HA2I model of HA2. (Middle) Average QS1–S1 (black) and QS5–S5 (red) for the two routes bifurcating from basin E. The two coordinates increase concommitantly in the cooperative route.
Experimentally, the HA2 transition has been found to be irreversible (1), implying that HA2F is much more stable than HA2I and only the I-to-F transition is of interest. The greater energetic stability of HA2F is captured within this model by the higher number of atom-atom native contacts in the HA2F structure (∼4,500) than in the HA2I structure (∼3,000). Accordingly, we characterized the kinetic intermediates along the transition using simulations that were initiated in the HA2I conformation and were terminated once they reached the HA2F ensemble (Fig. 2). In these simulations, we find that the dynamics within any HA2 transition can be separated into a fast and a slow phase based on the rate of events relative to that of S5I unfolding. Once S5I unfolds, the protein rapidly adopts the HA2F configuration.
Competing Interactions Drive the HA2 Transition.
The biological function of HA2 is to introduce and insert the fusion peptides into the host membrane. Fusion peptide insertion must occur before the C-terminal domains (S5) melt from the HA2I configuration and adopt the HA2F configuration (Discussion). Without a local energetic bias toward the HA2I configuration, S5I would immediately melt. Therefore, any model of functional HA2 must contain stabilizing interactions from both the HA2I and HA2F crystal conformations, necessitating at minimum a two-basin representation (Materials and Methods).
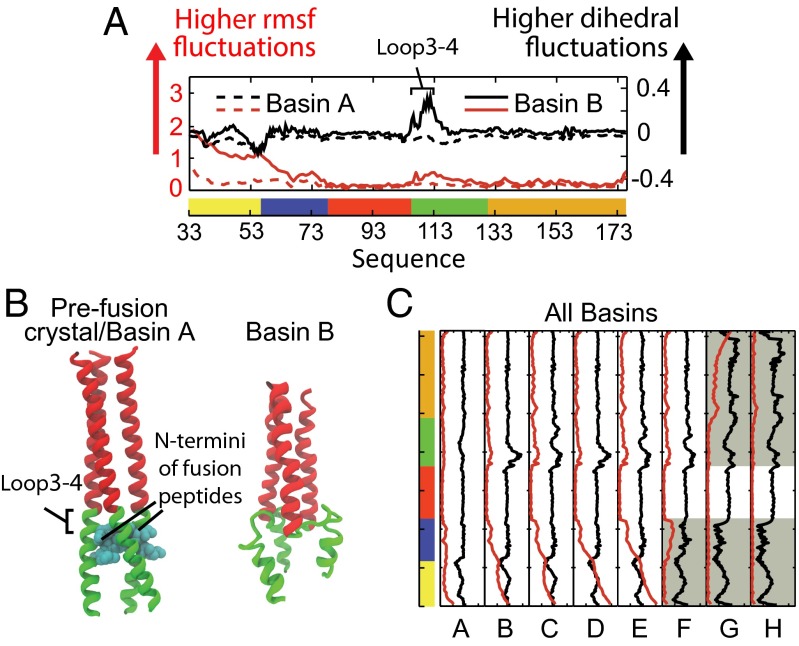
The dual-basin implementation sheds insights on the driving force for the HA2 conformational transition. Simulations using a single-basin model for HA2I exhibit local fluctuations about Basin A (Fig. 2, Inset), but unfolding is never observed. The dual-basin potential destablizes Loop3-4 (Fig. 3) through local interactions with the HA2F Hamiltonian and allows HA2 to leave basin A. Furthermore, in a dual-basin model (upon removal of HA1) the HA2I configuration is no longer a stable minimum on the free-energy surface, and the mean time spent in basin A τA is only 1% of the overall mean transition time τtrans (i.e., τA/τtrans = 0.011).
Fig. 3.
Disorder during the HA2 conformational change. (A) Initial cracking event (basins A and B) in the HA2 S3/S4 interface (Loop3-4). Red curves show RMSF for each residue averaged over the three monomers. RMSF values are calculated as an average over each structure within a basin in all trajectories. The RMSF of S3 is virtually equivalent with respect to either reference. Black curves show a local dihedral disorder measure. This disorder measure quantifies the similarity between the dihedral angle distribution for a particular dihedral and a uniform distribution (fully disordered state) relative to fluctuations about HA2I, and is bounded between −1 and 1. A larger value means more overlap with a uniform distribution and thus more disorder, with a value of zero indicating that dihedral fluctuations are equivalent to those about the single-basin HA2I structure (SI Appendix). Notably, Loop3-4 undergoes an order to disorder transition from basin A to B, coinciding with the location that the N termini of the fusion peptides bury in the prefusion structure. (B) Representative structural picture showing that the disorder in Loop3-4 destroys the burial site for the fusion peptides. (C) RMSF and dihedral disorder data for all basins A–H. RMSF fluctuations are given relative to HA2I where the background is white, HA2F where shaded (minimum of the two fits is used). Threefold symmetry breaking in the fast phase (basins B to C, D to E) returns some local dihedral order in Loop3-4.
Fast Phase: Disorder, Cracking, and Threefold Symmetry Breaking.
In all simulations, the HA2 transition initiates with two rapid events. The helical residues in Loop3-4 locally disorder (Fig. 3B) from a combination of low helical propensity (effected from HA2F Hamiltonian) and an inherent lack of stability because of the cavity left behind when the fusion peptides move from their initial burial sites (Fig. 3A). Additionally, global torsion of HA2 helps the “arms” (S1 and S2) to break their native interdomain contacts (Fig. 2, basin B). This torsion is consistent with previous predictions by normal mode analysis (25). This combination of events allows the arms (and their attached fusion peptides) to extend away from their previously restrained positions. For the remainder of the fast phase (Fig. 2, basins B–E), the arms broadly sweep out the configuration space, reflected in their large root mean-square fluctuation (RMSF) with respect to either reference crystal structure (Fig. 3C).
The local disorder transition in Loop3-4 has additional consequences beyond allowing the arms to dissociate. One monomer of S4 bends antiparallel to the central trimeric coil as it refolds to its HA2F structure (Fig. 2, basins C and E). S5I is a relatively stable trimeric unit, and although fully folded, geometrically precludes two of the three S4 monomers from adopting their HA2F conformation. This leads to an asymmetric HA2 configuration, where the central coil is bent sideways and packed against one side of S5. The S4 monomer that bends antiparallel forms most of its HA2F contacts, causing a concurrent increase in Loop3-4 dihedral order as the symmetry is broken (Fig. 3, basins B to C, D to E).
A transient increase in local disorder that facilitates a conformational transition (Fig. 3, basins A to B), known as “cracking,” has been previously shown in other protein systems (26–28). Here, the conformational change from basin A to B has features similar to cracking; local disorder in S4 lowers the barrier of the transition by breaking S1I interfacial contacts. Although this mechanism seems unlike previously studied examples of cracking because S4 returns to a configuration that is structurally dissimilar to S4I, the configurations at either end of the transition are more ordered than the intermediate ensemble. Thus, we do not consider this to be a distinct mechanism from cracking.
Slow Phase: Conformational Transition Follows Two Dominant Routes.
From basin E, the protein proceeds via one of two routes to complete the transition (shown by the two arrows leaving basin E in Fig. 2). The first is a sequential route, where the S1 monomers associate before the S5I trimeric interface breaks. This route may appear to resemble the spring-loaded intermediate, but remains distinct in that the threefold symmetry of HA2 is broken and S2 often does not form a well-packed helical bundle before S5I breaks. The second is a cooperative route, where the S5I trimeric interface is broken before S1 domains overcome the entropic barrier to association. As S5 folds into its postfusion conformation, it forms interdomain contacts with S1-S4, cooperatively pushing the arms together. The unfolding of S5I, which is common to both routes, is the rate-limiting step in the HA2 transition.
Comparison of RMSF between basins E and F (Fig. 3) shows that S1 undergoes a disorder-to-order transition along the sequential route, suggesting that there may be a substantial entropic barrier to the formation of the helical trimeric interface. Additionally, comparisons of RMSF values between basins F and G show that S2 can remain disordered until tertiary contacts with S5 are formed, even if S1 has fully adopted the trimeric postfusion conformation. In the sequential route, S1 and S2 must overcome this entropic barrier with a conformational search, reflected in their high RMSF in basin E (Fig. 3). However, in the cooperative route, local guidance from interactions with S5 lowers the free-energy barrier to formation of the S1-S2F coiled-coil.
The two dominant routes share similar kinetic characteristics, except for the relative order of events between them (Fig. 2, Middle). The sequential route spends a relatively longer time at around Qtrans = 0.4, corresponding to basin F in Fig. 2. Here, the association of S1F happens before S5I breaks apart, whereas in the cooperative route, S1 and S5 move to their final conformations concurrently. In both the sequential and cooperative route, the breaking of S5I and subsequent formation of S5F interface contacts are the final events in the HA2 conformational transition.
Qualitative Transition Features Are Robust to Parameterization.
We calculated the folding routes and kinetics for four different Hamiltonians at varying temperatures (Table 1). Although in every case the conformational transition follows one of the same two previously discussed folding routes, the population of each route depends on the rate of the central coiled-coil formation (S1F association) relative to the rate of S5I melting. In particular, the type of threefold symmetry breaking observed in the fast phase of the vanilla model is extremely robust to changes in the Hamiltonian and is always observed. The melting of S5I is similar to unfolding a globular protein, where increasing temperature lowers the barrier to unfolding and thus lowers the unfolding time for S5I . Because the cooperative route is defined by S5I melting before S1F formation, the population of transitions through the cooperative route increases with temperature. Also, because S5I melting is the rate-limiting step in the transition, the overall rate of the transition increases with temperature.
Table 1.
Effects of changing model parameters on the transition route
| Model | T ∼ 0.8Tm | T ∼ 0.9Tm | T ∼ Tm |
| Homogeneous* | |||
| % Seq | 27 | 11 | 0 |
| 14 | 5.8 | 3.4 | |
| 42 | 19 | 55 | |
| 17 | 4.7 | 1.0 | |
| Increased S2 helicity† | |||
| % Seq | 83 | 38 | 0 |
| 5.5 | 3.1 | 2.4 | |
| 5.2 | 4.2 | 23 | |
| 17 | 3.6 | 1.3 | |
% Seq is the percentage of trajectories that go through the sequential route. and give the mean first passage times for the formation of S1F and the breaking of S5I, respectively. measures the first passage time for S1F formation independent of S5 cooperation (i.e., with immobilized S5I). Times are measured in units of at Tm. Values are averages over ≥100 independent trajectories for each parameter set.
The dual-basin SBM with both structures equally weighted.
Single-basin HA2F dihedral potential for S2.
Previous experimental studies (21) and secondary structure predictors (29) have both suggested that the S2 monomer has high helical propensity. Because this propensity may be underestimated by the dual-basin modeling of S2 that gives equal weight to backbone torsions of the loop configuration, we tested a Hamiltonian that has secondary-structure propensity only to the S2F configuration (fully helical). This perturbation reduces the time until S1F formation by limiting the conformational search time of S1 monomers. Smaller with a constant also means higher sequential route population. Finally, when HA2 is represented in its biological context of being anchored to the viral membrane, the transition shows qualitatively similar features (SI Appendix).
Discussion and Conclusion
A key step in the biological function of HA is insertion of fusion peptides into the host membrane (30). Our simulations focused on the conformational transition of HA2 that facilitates the interaction between fusion peptides and the host membrane leading to subsequent pore formation. Based on the kinetic intermediates observed in the HA2 simulations, a possible membrane-fusion mechanism is summarized in Fig. 4. Endocytosis is followed by a drop in pH, which causes HA1 to dissociate (31), allowing HA2 to subsequently undergo four refolding stages. (i) Loop3-4 cracks and the arms (S1 and S2) detach from the central helices of HA2, releasing the fusion peptides. (ii) One S4 monomer forms an antiparallel structure with respect to the central helices (S3), causing HA2 to bend toward the viral membrane and breaking the threefold symmetry. (iii) After reaching this asymmetric intermediate ensemble, the dynamics of HA2 can diverge into one of two routes, both of which may be energetically accessible. In the sequential route, S1 first adopts its final trimeric arrangement, leading to a configuration where all fusion peptides can be inserted into the host membrane. In the cooperative route, one or two fusion peptides may insert into the viral membrane and the remaining into the host membrane. (iv) In the last stage of both routes, the C-terminal domain (S5I) melts and wraps HA2 into its final compact configuration. This step is likely very important for fusion because the viral transmembrane domains are attached to S5. Thus, in the HA2F configuration the fusion peptides are in the same (presumably fused) membrane as the transmembrane domains. If at any point S5I breaks before at least one fusion peptide is inserted in the host membrane, the conformational change may sterically restrict the fusion peptides near the viral surface, likely leading to an inactive HA2. The dual-funneled landscape of HA2 has evolved to avoid this fate (Fig. 5). Influence from the HA2F funnel encourages cracking that expedites HA2 reaching a fusogenic configuration. The HA2I funnel kinetically traps S5I to provide sufficient time delay for insertion of the fusion peptides into a membrane.
Fig. 4.
Cartoon illustrating the HA2 conformational transition with respect to viral and host membranes. The sections and color scheme applied here is the same as that in Fig. 1. Three black curves represent linkers connecting S5 to transmembrane anchors, depicted as three thicker black lines in the viral membrane. After dissociation of HA1, S4 cracks, releasing S1 and S2 from the central stalk. This is followed by a break in the threefold symmetry of HA2. The stochastic search of the arms can lead to all three fusion peptides inside the host membrane. However, because of the broken symmetry, they may also be closely apposed to and, as a result, inserted into the viral membrane. During the entire process, if S5 breaks before any fusion peptide reaches the host membrane, the conformational change will pin the fusion peptides to the viral membrane and invert HA2 with respect to its initial orientation, thus rendering it unable to participate in fusion.
Fig. 5.
Schematic picture of the HA dual-funneled energy (Upper, solvent-averaged energy) and free-energy (Lower, solvent-averaged energy plus conformational entropy) landscape. Microscopic Hamiltonian mixing means equally considering all contacts from HA2I and HA2F at all times. This has two main consequences: (i) the energy landscape contains a local energetic minimum with S5I and S1F formed (basin F in Fig. 2), and (ii) the kinetic barrier to leaving the HA2I basin is reduced by cracking induced by competition between HA2I and HA2F contacts (detailed in Fig. 3). On such a landscape, the unfolding of S5I becomes decoupled from forming the HA2F coiled-coil, allowing the S5I unfolding barrier to delay the transition. We hypothesize that a delay is functionally important because the fusion peptides require sufficient time to interact with and insert into a membrane.
A previously suggested “spring-loaded” model of HA function explains that HA1 removal releases HA2 from a metastable compact fold and that formation of the extended coiled-coil enthalpically drives HA2 toward a conformation that facilitates interaction with the host (21). Our presented mechanism shares similarities with this picture. First, the HA2I conformation is observed to be metastable because HA1 removal causes an immediate structural rearrangement of HA2. Second, an extended coiled-coil kinetic intermediate has significant population (basin F in Fig. 2). The key difference lies in the molecular mechanism of the transition. Instead of the coil-to-helix transition of S2 mechanically driving the molecule away from the HA2I structure in the “spring-loaded” model, our simulations suggest that the disorder in Loop3-4 (Fig. 3) and subsequent symmetry breaking of S4 (Fig. 2, basins C, E, and F) disrupts the binding sites for the fusion peptides and expedite their release. Here, the dual-basin nature of S2 does not provide a strong bias toward the coiled-coil S2F structure, leading to a kinetic intermediate where the HA2 arms (S1 and S2) are disordered (basin E in Fig. 2). In this intermediate, the symmetry breaking in S4 bends HA2 toward the viral membrane, localizing fusion peptides more closely to the viral membrane. The threefold symmetry breaking has been previously proposed as the last stage of conformational transition for HA2 and other retrovirus fusion proteins, which serves to bring the host and viral membranes closer together (3, 32). However, our results indicate that this event occurs earlier in the conformational transition than previously suggested. Coupled with previous work, which suggests that the fusion peptides are able to insert into both the host and viral membrane (11, 33, 34), this allows a fusogenic configuration of HA2 where the three fusion peptides are divided between the viral and host membranes. When S5I breaks, the refolding of S5F cooperatively aids in formation of the HA2F coiled-coil. This cooperative route is especially interesting when considering that the free energy released during the HA2 conformational transition can be used to assist in the subsequent membrane fusion (22). Because the HA2F coiled-coil is not formed when S5I breaks in the cooperative route, the free energy gained by forming its well-packed hydrophobic core can still be available during fusion. This is why we distinguish between the sequential and cooperative route: any free energy gained by refolding S5 is always available for fusion, but it can also be cooperatively added to the free energy gained by formation of the coiled-coil.
Our description leads to predictions that can be experimentally tested. For example, the increase of temperature will contribute to increased fusion activity until a point where the timescale of S5I dissociation is comparable to the timescale of fusion peptide insertion into the host membrane. As previously mentioned, S5I breaking apart before any fusion peptide has inserted into the host can lead to an HA2 with its fusion peptides pinned to the viral membrane, which is likely inactive. Therefore, we expect fusion activity to level off—or even decrease—as the temperature is increased beyond this threshold. The stability of S5 can also be tuned with denaturants, and addition of denaturant may be a more accessible experimental parameter. Mutagenesis of S5 to yield S5I of different stabilities can also be used to modulate the rate of S5I unfolding. The simulations highlight a subset of contacts that, when broken, are causally related to the unfolding of S5I (SI Appendix). Additionally, either single molecule or ensemble FRET could be used to examine the kinetics of S1 coiled-coil formation. In our suggested scenario, there would be a double exponential distribution for the rate of S1 association, one representing the S1 trimer forming in a spring-loaded manner, and another representing S1 association assisted by interactions with S5.
In conclusion, we have presented a minimally frustrated all-atom model to explore the extensive conformational rearrangement of influenza HA2. The dual-basin landscape of HA2 shows that native interactions from the HA2F crystal structure cause metastability of the HA2I conformation. Local disorder transitions in Loop3-4 present a mechanism for the release of the fusion peptides, which shows HA2 to be another example where local disorder enables a biomolecular functional motion (28). The interplay between the energetic stability of the S5I trimer and the entropic barrier toward S1F creates a quasi-stable kinetic intermediate, which in turn allows for parallel routes in the HA2 conformational transition: a sequential route and a cooperative route, where the latter suggests a similar role for the HA2 coiled-coil as in membrane fusion by the SNARE complexes. This understanding provides new insight into the function of influenza HA and other class I viral fusion proteins, which are thought to operate by a similar mechanism (35).
Materials and Methods
To study the transition, the principles of energy landscape theory were implemented through a structure-based model (SBM) (i.e., explicitly encoding the HA2I and HA2F crystal structures as deep energetic minima in the simulation Hamiltonian). An SBM reduces the complexity of molecular interactions by setting interactions between atoms that are close in the crystal structure as attractive and ignoring all others. The Hamiltonians for the two structures can be combined into a multibasin SBM through a global (macroscopic) mixing function (26) or combined locally (microscopic) by including all interactions present in both structures simultaneously (19, 36, 37). We adopted the local model for two reasons: (i) the endpoints are so disparate that in a macroscopic mixing model the barrier would be insurmountable, and (ii) we find that locally competing contacts serve as the driving force to facilitate the transition. The set of native contacts, atom pairs that are in proximity in the native structure, is called a contact map and uniquely defines the atom pairs given attractive interactions. Here, we used the “Shadow” criterion to define native contact maps for both the HA2I and HA2F structures (38). The dual-basin SBM contact map was created by combining all native contacts from both conformations and giving each contact equal strength (19). All other pair interactions were modeled as hard spheres to maintain excluded volume. Langevin dynamics was used to sample the SBM. A complete description of the dual-basin SBM and simulation protocols is given in the SI Appendix.
HA1 was not represented in the simulations, despite the disulfide bond that anchors it to HA2. Our rationale is based on the observation that the primary role of HA1 during the conformational transition is simply to prevent HA2 from undergoing premature conformational change. It is known that the HA2 trimer without HA1 forms the postfusion structure (22, 39) and that HA1 undergoes no conformational change at low pH (7). The tendency for HA1 to dissociate at low pH can be easily understood from the high isoelectric point of the HA1 (pI∼8) compared with HA2 (pI∼5) (40). Therefore, for simplicity, we removed HA1 from the model.
Supplementary Material
Acknowledgments
This work was supported by the Center for Theoretical Biological Physics sponsored by the National Science Foundation (Grant PHY-1427654); NSF-MCB-1214457; Welch Foundation Grant C-1792; National Science Foundation CAREER Award Grant MCB-1350312 (to P.C.W.); National Institutes of Health Grant R01-AI067839 (to Q.W.); the Welch Foundation (Q-1826) (to Q.W.); the Gillson-Longenbaugh Foundation (Q.W.); National Institutes of Health Grant R01-GM067801 (to J.M.); National Science Foundation Grant MCB-0818353 (to J.M.); and the Welch Foundation (Q-1512) (to J.M.). J.N.O. is a Cancer Prevention Research Institute of Texas Scholar in Cancer Research sponsored by the Cancer Prevention and Research Institute of Texas.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1412849111/-/DCSupplemental.
References
- 1.Skehel JJ, Wiley DC. Receptor binding and membrane fusion in virus entry: The influenza hemagglutinin. Annu Rev Biochem. 2000;69:531–569. doi: 10.1146/annurev.biochem.69.1.531. [DOI] [PubMed] [Google Scholar]
- 2.Skehel JJ, Wiley DC. Coiled coils in both intracellular vesicle and viral membrane fusion. Cell. 1998;95(7):871–874. doi: 10.1016/s0092-8674(00)81710-9. [DOI] [PubMed] [Google Scholar]
- 3.Hughson FM. Enveloped viruses: A common mode of membrane fusion? Curr Biol. 1997;7(9):R565–R569. doi: 10.1016/s0960-9822(06)00283-1. [DOI] [PubMed] [Google Scholar]
- 4.Wilson IA, Skehel JJ, Wiley DC. Structure of the haemagglutinin membrane glycoprotein of influenza virus at 3 A resolution. Nature. 1981;289(5796):366–373. doi: 10.1038/289366a0. [DOI] [PubMed] [Google Scholar]
- 5.Carr CM, Chaudhry C, Kim PS. Influenza hemagglutinin is spring-loaded by a metastable native conformation. Proc Natl Acad Sci USA. 1997;94(26):14306–14313. doi: 10.1073/pnas.94.26.14306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bullough PA, Hughson FM, Skehel JJ, Wiley DC. Structure of influenza haemagglutinin at the pH of membrane fusion. Nature. 1994;371(6492):37–43. doi: 10.1038/371037a0. [DOI] [PubMed] [Google Scholar]
- 7.Bizebard T, et al. Structure of influenza virus haemagglutinin complexed with a neutralizing antibody. Nature. 1995;376(6535):92–94. doi: 10.1038/376092a0. [DOI] [PubMed] [Google Scholar]
- 8.Park HE, Gruenke JA, White JM. Leash in the groove mechanism of membrane fusion. Nat Struct Biol. 2003;10(12):1048–1053. doi: 10.1038/nsb1012. [DOI] [PubMed] [Google Scholar]
- 9.Melikyan GB, Niles WD, Cohen FS. The fusion kinetics of influenza hemagglutinin expressing cells to planar bilayer membranes is affected by HA density and host cell surface. J Gen Physiol. 1995;106(5):783–802. doi: 10.1085/jgp.106.5.783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bentz J. Minimal aggregate size and minimal fusion unit for the first fusion pore of influenza hemagglutinin-mediated membrane fusion. Biophys J. 2000;78(1):227–245. doi: 10.1016/S0006-3495(00)76587-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bentz J. Membrane fusion mediated by coiled coils: A hypothesis. Biophys J. 2000;78(2):886–900. doi: 10.1016/S0006-3495(00)76646-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bentz J, Mittal A. Architecture of the influenza hemagglutinin membrane fusion site. Biochim Biophys Acta. 2003;1614(1):24–35. doi: 10.1016/s0005-2736(03)00160-3. [DOI] [PubMed] [Google Scholar]
- 13.Madhusoodanan M, Lazaridis T. Investigation of pathways for the low-pH conformational transition in influenza hemagglutinin. Biophys J. 2003;84(3):1926–1939. doi: 10.1016/S0006-3495(03)75001-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Onuchic JN, Wolynes PG. Theory of protein folding. Curr Opin Struct Biol. 2004;14(1):70–75. doi: 10.1016/j.sbi.2004.01.009. [DOI] [PubMed] [Google Scholar]
- 15.Bryngelson JD, Wolynes PG. Spin-glasses and the statistical-mechanics of protein folding. Proc Natl Acad Sci USA. 1987;84(21):7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Leopold PE, Montal M, Onuchic JN. Protein folding funnels: A kinetic approach to the sequence-structure relationship. Proc Natl Acad Sci USA. 1992;89(18):8721–8725. doi: 10.1073/pnas.89.18.8721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Whitford PC, et al. An all-atom structure-based potential for proteins: Bridging minimal models with all-atom empirical forcefields. Proteins. 2009;75(2):430–441. doi: 10.1002/prot.22253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Noel JK, Whitford PC, Sanbonmatsu KY, Onuchic JN. SMOG@ctbp: Simplified deployment of structure-based models in GROMACS. Nucleic Acids Res. 2010;38(Web Server issue):W657–W661. doi: 10.1093/nar/gkq498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Noel JK, et al. Mirror images as naturally competing conformations in protein folding. J Phys Chem B. 2012;116(23):6880–6888. doi: 10.1021/jp212623d. [DOI] [PubMed] [Google Scholar]
- 20.Lammert H, Schug A, Onuchic JN. Robustness and generalization of structure-based models for protein folding and function. Proteins. 2009;77(4):881–891. doi: 10.1002/prot.22511. [DOI] [PubMed] [Google Scholar]
- 21.Carr CM, Kim PS. A spring-loaded mechanism for the conformational change of influenza hemagglutinin. Cell. 1993;73(4):823–832. doi: 10.1016/0092-8674(93)90260-w. [DOI] [PubMed] [Google Scholar]
- 22.Chen J, Skehel JJ, Wiley DC. N- and C-terminal residues combine in the fusion-pH influenza hemagglutinin HA(2) subunit to form an N cap that terminates the triple-stranded coiled coil. Proc Natl Acad Sci USA. 1999;96(16):8967–8972. doi: 10.1073/pnas.96.16.8967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cho SS, Levy Y, Wolynes PG. P versus Q: Structural reaction coordinates capture protein folding on smooth landscapes. Proc Natl Acad Sci USA. 2006;103(3):586–591. doi: 10.1073/pnas.0509768103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Best RB, Hummer G, Eaton WA. Native contacts determine protein folding mechanisms in atomistic simulations. Proc Natl Acad Sci USA. 2013;110(44):17874–17879. doi: 10.1073/pnas.1311599110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Isin B, Doruker P, Bahar I. Functional motions of influenza virus hemagglutinin: A structure-based analytical approach. Biophys J. 2002;82(2):569–581. doi: 10.1016/S0006-3495(02)75422-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Okazaki K, Koga N, Takada S, Onuchic JN, Wolynes PG. Multiple-basin energy landscapes for large-amplitude conformational motions of proteins: Structure-based molecular dynamics simulations. Proc Natl Acad Sci USA. 2006;103(32):11844–11849. doi: 10.1073/pnas.0604375103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Miyashita O, Onuchic JN, Wolynes PG. Nonlinear elasticity, proteinquakes, and the energy landscapes of functional transitions in proteins. Proc Natl Acad Sci USA. 2003;100(22):12570–12575. doi: 10.1073/pnas.2135471100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Whitford PC, Sanbonmatsu KY, Onuchic JN. Biomolecular dynamics: Order-disorder transitions and energy landscapes. Rep Prog Phys. 2012;75(7):076601. doi: 10.1088/0034-4885/75/7/076601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Buchan DWA, Minneci F, Nugent TCO, Bryson K, Jones DT. Scalable web services for the psipred protein analysis workbench. Nucleic Acids Res. 2013;41(Web Server issue):W349–W357. doi: 10.1093/nar/gkt381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gething MJ, Doms RW, York D, White J. Studies on the mechanism of membrane fusion: Site-specific mutagenesis of the hemagglutinin of influenza virus. J Cell Biol. 1986;102(1):11–23. doi: 10.1083/jcb.102.1.11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Godley L, et al. Introduction of intersubunit disulfide bonds in the membrane-distal region of the influenza hemagglutinin abolishes membrane fusion activity. Cell. 1992;68(4):635–645. doi: 10.1016/0092-8674(92)90140-8. [DOI] [PubMed] [Google Scholar]
- 32.Weissenhorn W, Dessen A, Harrison SC, Skehel JJ, Wiley DC. Atomic structure of the ectodomain from HIV-1 gp41. Nature. 1997;387(6631):426–430. doi: 10.1038/387426a0. [DOI] [PubMed] [Google Scholar]
- 33.Weber T, et al. Evidence for H(+)-induced insertion of influenza hemagglutinin HA2 N-terminal segment into viral membrane. J Biol Chem. 1994;269(28):18353–18358. [PubMed] [Google Scholar]
- 34.Wharton SA, et al. Electron microscopy of antibody complexes of influenza virus haemagglutinin in the fusion pH conformation. EMBO J. 1995;14(2):240–246. doi: 10.1002/j.1460-2075.1995.tb06997.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.White JM, Delos SE, Brecher M, Schornberg K. Structures and mechanisms of viral membrane fusion proteins: Multiple variations on a common theme. Crit Rev Biochem Mol Biol. 2008;43(3):189–219. doi: 10.1080/10409230802058320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Singh JP, Whitford PC, Hayre NR, Onuchic J, Cox DL. Massive conformation change in the prion protein: Using dual-basin structure-based models to find misfolding pathways. Proteins. 2012;80(5):1299–1307. doi: 10.1002/prot.24026. [DOI] [PubMed] [Google Scholar]
- 37.Lu Q, Wang J. Single molecule conformational dynamics of adenylate kinase: Energy landscape, structural correlations, and transition state ensembles. J Am Chem Soc. 2008;130(14):4772–4783. doi: 10.1021/ja0780481. [DOI] [PubMed] [Google Scholar]
- 38.Noel JK, Whitford PC, Onuchic JN. The shadow map: A general contact definition for capturing the dynamics of biomolecular folding and function. J Phys Chem B. 2012;116(29):8692–8702. doi: 10.1021/jp300852d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Chen J, et al. A soluble domain of the membrane-anchoring chain of influenza virus hemagglutinin (HA2) folds in Escherichia coli into the low-pH-induced conformation. Proc Natl Acad Sci USA. 1995;92(26):12205–12209. doi: 10.1073/pnas.92.26.12205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lu Y, Welsh JP, Swartz JR. Production and stabilization of the trimeric influenza hemagglutinin stem domain for potentially broadly protective influenza vaccines. Proc Natl Acad Sci USA. 2014;111(1):125–130. doi: 10.1073/pnas.1308701110. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.