Skip to main content
. 2014 Jun 20;16(5):925–937. doi: 10.1208/s12248-014-9632-5

Fig. 2.

Fig. 2

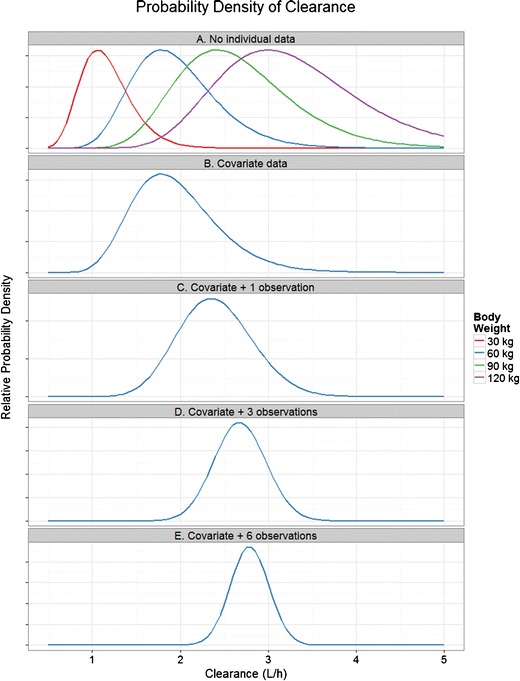
An example of the contribution of individual data to Bayes forecasts. The example uses a simple one parameter, one covariate model for the steady-state drug concentration (C ss) of a chronically administered drug: C ss = DoseRate/(CL × (WT/70)0.75). CL is a log-normally distributed population parameter with a population value of 2 L/h and a between-subject variability of 25%. WT is a covariate for body weight affecting CL via an allometric relationship, where the standard body weight is 70 kg. DoseRate is the average steady-state dose rate—set at 10 mg/h, proportional residual error for the model was 20%. We wish to forecast the clearance of the drug (so that individual C ss can be estimated). Panel A shows the probability densities for CL for the case where no individual information is known about the patient (densities are normalized to the same peak value for clarity). There are a variety of possible distributions for CL, depending on the unknown body weight of the patient. Panel B shows the distribution of CL with covariate data. The patient has a weight of 60 kg, eliminating other candidate distribution curves. Panel C shows the distribution of CL with covariate data and a single observation of C ss in the patient (C ss was found to be 4 mg/L, lower than the expected value of 5.6 mg/L for a 60 kg subject). The distribution has therefore moved to the right, reflecting higher individual clearance and has become narrower, reflecting more certainty about the individual value of CL. Panels D and E show the distribution of CL with covariate data and 3 and 6 observations of C ss in the patient. Note that as more individual data are available, the uncertainty in the distribution of CL reduces (i.e., the distributions are narrower)