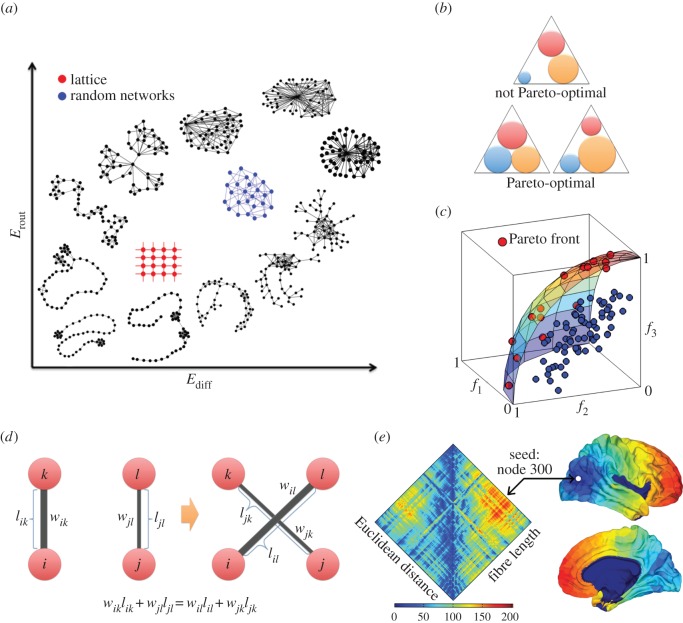
Figure 1.

(a) Diagram of a communication-efficiency morphospace for toy-networks; the location of a toy-network within this morphospace of abstract networks can be associated with specific aspects of network structure that favour two distinct communication schemes: diffusion-based communication (E_diff) and routing-based communication (E_rout). (b) Geometric example of Pareto optimality: the area of three circles represents three objectives to be maximized; circles are constrained to be contained within an equilateral triangle and cannot overlap with each other. There are several solutions to the problem; the top triangle shows a solution that could be improved by increasing the area of the blue circle; thus, it is not Pareto-optimal. The two bottom triangles show solutions in which the area of none of the circles can be increased without having to decrease the area of another circle; therefore, the solutions are Pareto-optimal [45]. (c) Example of a Pareto front, where three objective functions are to be maximized. All the points in the plot represent feasible solutions; however, only the red points belong to the Pareto front. (d) Rewiring rule: the weights of the edges {i, l} and {j, k} are randomly selected, provided that the total wiring cost is preserved. (e) Matrix of Euclidean distances (left side) and interpolated fibre lengths (right side) between all pairs of nodes of the LAU1 dataset. The colour map on the human cortex images represents the fibre lengths after interpolation between node 300 (whose location is indicated with a white circle) and all other nodes of the LAU1 network.