Figure 2.

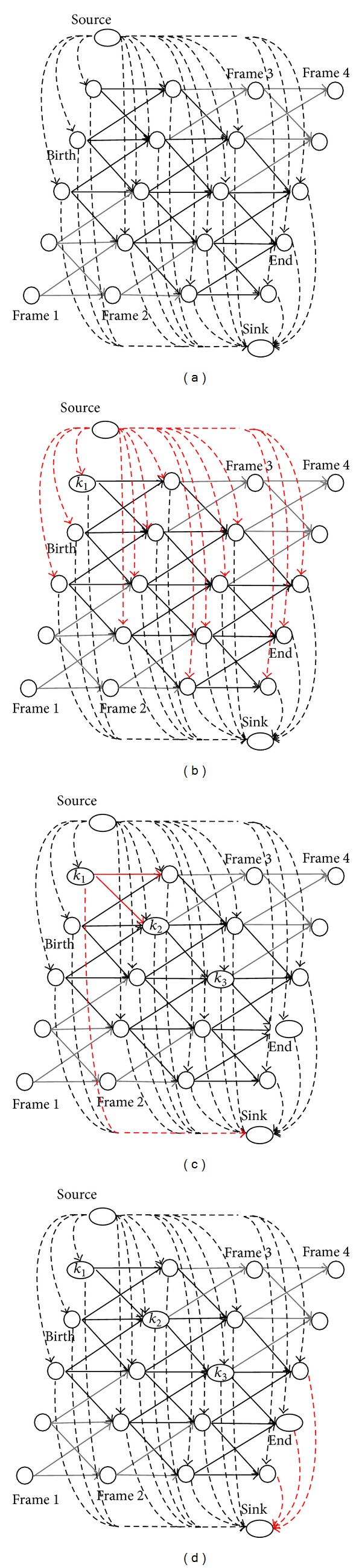
The shortest path faster algorithm. (a) Recording all nodes of G _r in an adjacency list, starting from the source node. Adding the source into the queue Q, let D(source) = 0; (b) adding all the nodes that can be reached from source to Q and recording the cost values in D. (c) Adding all nodes that can be reached from k ₁ to Q and recording their total cost values. If a node has been in queue Q, update its total cost value to the smaller value in D; (d) iterating (c) until queue Q is empty and the shortest path T = (k ₁,…, k _N), k _N ∈ G _r from source to sink can be obtained at the same time. Legend: black solid line, all edges among positions that can be reached, red solid line, all edges from the current position to potential locations that can be reached, black dashed line, all edges between virtual positions and the potential locations that can be reached, and red dashed line, all edges from the current position (or virtual positions) to virtual positions (or potential locations) that can be reached.