The Flynn Effect: A Meta-analysis

Abstract

The “Flynn effect” refers to the observed rise in IQ scores over time, resulting in norms obsolescence. Although the Flynn effect is widely accepted, most approaches to estimating it have relied upon “scorecard” approaches that make estimates of its magnitude and error of measurement controversial and prevent determination of factors that moderate the Flynn effect across different IQ tests. We conducted a meta-analysis to determine the magnitude of the Flynn effect with a higher degree of precision, to determine the error of measurement, and to assess the impact of several moderator variables on the mean effect size. Across 285 studies (N = 14,031) since 1951 with administrations of two intelligence tests with different normative bases, the meta-analytic mean was 2.31, 95% CI [1.99, 2.64], standard score points per decade. The mean effect size for 53 comparisons (N = 3,951) (excluding three atypical studies that inflate the estimates) involving modern (since 1972) Stanford-Binet and Wechsler IQ tests (2.93, 95% CI [2.3, 3.5], IQ points per decade) was comparable to previous estimates of about 3 points per decade, but not consistent with the hypothesis that the Flynn effect is diminishing. For modern tests, study sample (larger increases for validation research samples vs. test standardization samples) and order of administration explained unique variance in the Flynn effect, but age and ability level were not significant moderators. These results supported previous estimates of the Flynn effect and its robustness across different age groups, measures, samples, and levels of performance.

Historical Background

The “Flynn effect” refers to the observed rise over time in standardized intelligence test scores, documented by Flynn (1984a) in a study on intelligence quotient (IQ) score gains in the standardization samples of successive versions of Stanford-Binet and Wechsler intelligence tests. Flynn’s study revealed a 13.8-point increase in IQ scores between 1932 and 1978, amounting to a 0.3-point increase per year, or approximately 3 points per decade. More recently, the Flynn effect was supported by calculations of IQ score gains between 1972 and 2006 for different normative versions of the Stanford-Binet (SB), Wechsler Adult Intelligence Scale (WAIS), and Wechsler Intelligence Scale for Children (WISC) (Flynn, 2009a). The average increase in IQ scores per year was 0.31, which was consistent with Flynn’s (1984a) earlier findings.

The Flynn effect implies that an individual will likely attain a higher IQ score on an earlier version of a test than on the current version. In fact, a test will overestimate an individual’s IQ score by an average of about 0.3 points per year between the year in which the test was normed and the year in which the test was administered. The ramifications of this effect are especially pertinent to the diagnosis of intellectual disability in high stakes decisions when an IQ cut point is used as a necessary part of the decision-making process. The most dramatic example in the United States is the determination of intellectual disability in capital punishment cases. These determinations in so-called Atkins hearings represent life and death decisions for death row inmates scheduled for execution. Because an inmate may have received several IQ scores with different normative samples over time, whether to acknowledge the Flynn effect is a major bone of contention in the legal system. In addition, the Flynn effect figures in access to services and accommodations, such as determining eligibility for special education and American Disability Act services and Social Security Disability Insurance (SSDI) in the United States.

More generally, conceptions about IQ as a predictor of success in various domains is pervasive in many domains of the behavioral sciences and in Western societies. Many studies use IQ scores as an outcome variable or to characterize the sample. In clinical practice, most assessments routinely administer an IQ test and most applied training programs teach administration and interpretation of IQ test scores. Organizations like MENSA set IQ levels associated with “genius” and people commonly refer to others as “bright” or use more pejorative terms as an indicator of their level of ability. Although the meaningfulness of these uses of IQ scores is beyond the scope of this investigation, they illustrate the pervasiveness of concepts about IQ scores as indicators of individual differences and level of performance.

The Flynn effect is less well known and often not taught in behavioral science training programs (Hagen, Drogin, & Guilmette, 2008). It is important because the normative base of the test directly influences the interpretation of the level of IQ. MENSA, the “high IQ society,” requires an IQ score in the top 2% of the population (www.us.mensa.org/join/testscores/qualifyingscores). The organization accepts scores from a variety of tests, often with no specification of which version of the test. The Stanford-Binet IV and Stanford-Binet 5 are both permitted. If a person applied and took an IQ test in 2014, the required score of 132 on the Stanford-Binet 4 would be equivalent to a score of 126 on the recently normed Stanford-Binet 5 because the normative sample was formed 20 years ago. Although the Flynn effect is not necessarily of general interest to psychology, the pervasive use of IQ test scores in clinical practice and research, in high stakes decisions, and in Western society suggests that it should be. It is not surprising that a PsycINFO® search shows that the number of articles on the Flynn effect rose from 6 in 2001–2002 to 54 in 2010–2011. Most significant is the use of IQ scores in identifying intellectual disabilities and the death penalty, where there are literally hundreds of active cases in the judicial system, and in determining eligibility for social services and special education.

Definition of Intellectual Disability

The identification of an intellectual disability in the United States requires the presence of significant limitations in intellectual functioning and adaptive behavior prior to age 18 (American Association on Intellectual and Developmental Disabilities [AAIDD], 2010). An IQ score at least two standard deviations below the mean (i.e., ≤ 70) is a common indicator of a significant limitation in intellectual functioning, and captures approximately 2.2% of the population. Although the gold standard AAIDD criteria stress the importance of exercising clinical judgment in the interpretation of IQ scores (e.g., accounting for measurement error), a cut-off score of 70 commonly is used to indicate a significant limitation in intellectual functioning (Greenspan & Switzky, 2006). Thus, were an adult to have attained an IQ score of 73 on the Wechsler Intelligence Scale for Children--Revised (WISC-R) as a child, s/he might not be identified as having a significant limitation in intellectual functioning. However, suppose the WISC-R had been administered in 1992, 20 years after the test was normed. The Flynn effect would have inflated test norms by 0.3 points per year between the year in which the test was normed (1972) and the year in which the test was administered (1992). Correction for that inflation would reduce the person’s IQ score by six points, to 67, thereby indicating a significant limitation in intellectual functioning and highlighting the problems with obsolete norms. Further, the WISC-III, published in 1989, would have been the current edition of the test when the child was tested. This underscores the importance of testing practices (e.g., acquiring and administering the current version of a test) in formal education settings.

High Stakes Decisions

Capital punishment

The Eighth Amendment of the U.S. Constitution prohibits cruel and unusual punishment, and that prohibition informed the Court’s decision in Atkins v. Virginia (2002) to abstain from imposing the death penalty on a defendant with an intellectual disability. In this case, Daryl Atkins, a man determined to have a mild intellectual disability, was convicted of capital murder. The Supreme Court of Virginia initially imposed the death penalty on Atkins; however, the United States Supreme Court reversed the decision due to the presumed difficulty people with intellectual disabilities have in understanding the ramifications of criminal behavior and the emergence of statutes in a growing number of states barring the death penalty for defendants with an intellectual disability.

In 2008, a report indicated that since the reversal of the death penalty in Atkins’ case, 80+ death penalty pronouncements have been converted to life in prison (Blume, 2008). This number has increased significantly since 2008. Importantly, Walker v. True (2005) set a precedent for the consideration of the Flynn effect in capital murder cases. The defendant argued in an appeal that his sentence violated the Eighth Amendment; when corrected for the Flynn effect, his IQ score of 76 on the WISC, administered to the defendant in 1984 when he was 11 years old, would be reduced by four points to 72. He alleged that a score of 72 fell within the range of measurement error recognized by the AAIDD (2010) and the American Psychiatric Association (APA, 2000) for a true score of 70. The judges agreed that the Flynn effect and measurement error should be considered in this case. There are hundreds of Atkins hearings involving the Flynn effect in some manner and other issues related to the use of IQ tests (see AtkinsMR/IDdeathpenalty.com)

Special education

Demonstration of an intellectual disability or a learning disability is an eligibility criterion for receipt of special education services in schools. Kanaya, Ceci, and Scullin (2003a) and Kanaya, Scullin, and Ceci (2003b) documented a pattern of “rising and falling” IQ scores in children diagnosed with an intellectual disability or learning disability as a function of the release date of the new version of an intelligence test. One study (Kanaya et al., 2003a) mapped IQ scores obtained from children’s initial special education assessments between 1972 and 1977, during the transition from the WISC to the WISC-R, and between 1990 and 1995, during the transition from the WISC-R to the WISC-III. The authors reported a reduction in IQ scores during the fourth year of each interval (one year after the release of the new test version) followed by an increase in IQ scores during subsequent years. In a second study (Kanaya et al., 2003b), the authors reported a 5.6-point reduction in IQ score for children initially tested with the WISC-R and subsequently tested with the WISC-III, with a significantly greater proportion of these children being diagnosed with an intellectual disability during the second assessment than children who completed the same version of the WISC during both assessments. More recent studies have supported these patterns in children assessed for learning disabilities with the WISC-III (Kanaya & Ceci, 2012).

Taken together, these studies suggest that the use of obsolete norms leads to inflation of the IQ scores of children referred for a special education assessment as a function of the time between the year in which the test was normed and the year in which the test was administered. The use of a test with obsolete norms reduces the likelihood of a child being identified with an intellectual disability and receiving appropriate services, and may increase the prevalence of learning disabilities; the inflated IQ score helps produce a discrepancy between intellectual functioning and achievement, which in education settings has often been interpreted as indicating a learning disability (Fletcher et al., 2007). These studies also highlight the importance of using the current version of a test in education settings, a practice which may be thwarted by a school district’s budgetary constraints and challenges associated with learning the administration and scoring procedures for the new test (Kanaya & Ceci, 2007).

Social security disability

As with determination of the death penalty and eligibility for special education, IQ testing remains an important component of the decision-making process for determining eligibility for SSDI as a person with an intellectual disability. Like the AAIDD, the Social Security Administration (2008) requires significant limitations in intellectual functioning and adaptive behavior for a diagnosis of intellectual disability; however, these limitations must be present prior to age 22. Moreover, individuals with an IQ at or below 59 are eligible de facto for SSDI, whereas those with an IQ between 60 and 70 must demonstrate work-related functional limitations resulting from a physical or other mental impairment, or two other specified functional limitations (e.g., social functioning deficits). The manual, like the AAIDD manual, explicitly discusses the importance of correcting for the Flynn effect, but acknowledges that precise estimates are not available.

Flynn’s Work

Flynn’s (1984a) landmark study, which revealed increasing IQ at a median rate of 0.31 points per year between 1932 and 1978 across 18 comparisons of the SB, WAIS, WISC, and Wechsler Preschool and Primary Scale of Intelligence (WPPSI), was the first analysis of its kind. Seventy-three studies totaling 7,431 participants provided support for this effect. Whereas Flynn’s (1984a) study focused on comparisons documented in publication manuals of primarily the first editions of the Stanford-Binet and Wechsler tests, a second study investigated IQ gains in 14 developed countries using a variety of instruments, including Ravens Progressive Matrices, Wechsler, and Otis-Lennon tests (Flynn, 1987). IQ gains amounted to a median of 15 points in one generation, described by Flynn (1987) as “massive.” An extension of Flynn’s (1984a) work documented a mean rate of IQ gain equaling approximately 0.31 IQ points per year across 12 comparisons of the SB, WAIS, and WISC standardization samples (Flynn, 2007), a value highly consistent with earlier findings. Further, 14 comparisons of Stanford-Binet and Wechsler standardization samples, accounting for the recent publication of the WAIS-IV, revealed an annual rate of IQ gain equaling 0.31 (Flynn, 2009a). These latter findings, based on the simple averaging of IQ gains across studies, were supported by the only meta-analysis addressing the Flynn effect (Fletcher, Stuebing, & Hughes, 2010). For these 14 studies, Fletcher et al. (2010) calculated a weighted mean rate of IQ gain of 2.80 points per decade, 95% CI [2.50, 3.09], and a weighted mean rate of IQ gain of 2.86, 95% CI [2.50, 3.22], after excluding comparisons that included the WAIS-III because effect sizes produced by comparisons between the WAIS-III and another test differed considerably from the effect sizes produced by comparisons between other tests. The puzzling effects produced by comparisons including the WAIS-III were consistent with Flynn’s (2006a) study, wherein he demonstrated that IQ score inflation on the WAIS-III was reduced because of differences in the range of possible scores at the lower end of the distribution.

Other notable investigations conducted by Flynn include the computation of a weighted average IQ gain per year of 0.29 between the WISC and WISC-R across 29 studies comprising 1,607 subjects (1985): a rate of IQ gain per year of 0.31 between the WISC-R and the WISC-III across test manual studies and a selection of studies carried out by independent researchers (1998a); and a rate of IQ gain per year of 0.20 between the WAIS-R and WAIS-III across test manual studies (1998a). Prior to these studies, Flynn (1984b) also reported SB gains across standardization samples, and both real and simulated gains for the WPPSI and the first two versions of the WISC and WAIS. Flynn (1988b) noted consistent gains between the WISC (N = 93) and WISC-R (N = 296) in Scottish children (1990); for the Matrices and Instructions tests in an Israeli military sample totaling approximately 26,000 subjects per year between 1971 and 1984; between the WISC-III and an earlier version of the test in samples from the United States, West Germany, Austria, and Scotland totaling 3,190 subjects (2000); and for the Coloured Progressive Matrices in British standardization samples totaling 1,833 participants (2009b). The existence of the Flynn effect is rarely disputed. However, a working magnitude and measurement error associated with the Flynn effect are not well established, leaving unanswerable the question of how much of a correction – if any – to apply to IQ test scores to account for the norming date of the test. Further, there is considerable contention over factors that may cause the Flynn effect (Flynn, 2007, 2012; Neisser, 1998).

Proposed Causes of the Flynn Effect

There are multiple hypotheses about the basis for the Flynn effect, including genetic and environmental factors, and measurement issues.

Genetic hypotheses

Mingroni (2007) hypothesized that IQ gains are the result of increasingly random mating, termed heterosis (or hybrid vigor), a phenomenon that produces changes in traits governed by the combination of dominant and recessive alleles. However, Lynn (2009) noted that the Flynn effect in Europe has mirrored the effect in the United States despite evidence of minimal migration to Europe prior to 1950 and limited inter-mating between native and immigrant populations since then. A more comprehensive argument against a genetic cause for the Flynn effect has been made by Woodley (2011).

Environmental factors

Woodley (2011) argued that “The [Flynn] effect only concerns the non-g variance unique to specific cognitive abilities” (p. 691), presumably bringing environmental explanations for the Flynn effect to the forefront. Environmental factors hypothesized as moderators of the Flynn effect include sibship size (Sundet, Borren, & Tambs, 2008) and pre-natal and early post-natal nutrition (Lynn, 2009). In Norway, Sundet et al. demonstrated that an increase in IQ scores paralleled a decrease in sibship size, with the greatest increase in IQ scores occurring between cohorts with the greatest decrease in sibship size. For example, between birth cohort 1938–1940 and 1950–1952, the percentage of sibships composed of 6+ children decreased from 20% to 5%, and IQ score increased by 6 points.

With rates of Development Quotient score gains in infants mirroring IQ score gains of preschool children, school-aged children, and adults, Lynn (2009) questioned the validity of explanations whose effects would emerge later in development, such as improvements in child rearing (Elley, 1969) and education (Tuddenham, 1948); increased environmental complexity (Schooler, 1998), test sophistication (Tuddenham, 1948), and test-taking confidence (Brand, 1987); and the effects of genetics (Jensen, 1998) and the individual and social multiplier phenomena (Dickens & Flynn, 2001a; Dickens & Flynn, 2001b). Lynn (2009) proposed improvements in pre- and post-natal nutrition as likely causes of the Flynn effect, citing a parallel increase in infants of other nutrition-related characteristics, including height, weight, and head circumference. Improvement to the prenatal environment is also supported by trends in the reduction of alcohol and tobacco use during pregnancy (Bhuvaneswar, Chang, Epstein, & Stern, 2007; Tong, Jones, Dietz, D’Angelo, & Bombard, 2009).

Neisser (1998) suggested that increasing IQ scores have mirrored socioenvironmental changes in developing countries. If IQ test score changes are a product of socioenvironmental improvements, then as living conditions optimize, IQ scores should plateau. This suggestion has been echoed by Sundet, Barlaug, and Torjussen (2004), who documented a plateau in IQ scores in Norway (Sundet et al., 2004) and speculated that changes in family life factors (e.g., family size, parenting style, and child care) might be partly responsible for this pattern. A decline in IQ scores has even been noted in Denmark (Teasdale & Owen, 2008; Teasdale & Owen, 2005), a pattern that the authors suggested might be due to a shift in educational priorities toward more practical skills manifest in the increasing popularity of vocational programs for post-secondary education.

Although Flynn (2010) acknowledged that his “scientific spectacles” hypothesis may no longer explain current IQ gains, he maintained that there was a period of time when it was the foremost contributor. Putting on “scientific spectacles” refers to the tendency of contemporary test takers to engage in formal operational thinking, as evidenced by a massive gain of 24 IQ points on the Similarities subtest of the WISC, a measure of abstract reasoning, between 1947 and 2002, a gain unparalleled by any other subtest (Flynn & Weiss, 2007). Conceptualizing IQ gains as a shift in thinking style from concrete operational to formal operational rather than an increase in intelligence per se would explain why previous generations thrived despite producing norms on IQ tests that overestimated the intellectual abilities of future generations (Flynn, 2007). However, this difference may be more simply attributed to changes across different versions of Similarities and other verbal subtests (Kaufman, 2010) of the WISC. Nonetheless, Dickinson and Hiscock (2010) reported a Flynn effect for WAIS Similarities of 4.5 IQ points per decade for WAIS to WAIS-R and 2.6 IQ points per decade for WAIS-R to WAIS-III. The average was 3.6 IQ points per decade or 0.36 IQ points per year. This change in adult performance is only moderately less than Flynn’s 0.45 points per year for the WISC between 1947 and 2002.

Measurement issues

Tests of verbal ability, compared with performance-based measures, have been reported to be less sensitive to the Flynn effect (Flynn, 1987; Flynn, 1994; Flynn, 1998b; Flynn, 1999), which may be related to changes in verbal subtests. Beaujean and Osterlind (2008) and Beaujean and Sheng (2010) used Item Response Theory (IRT) to determine whether increases in IQ scores over time reflect changes in the measurement of intellectual functioning rather than changes in the underlying construct, i.e., the latent variable of cognitive ability. Although changes in Peabody Picture Vocabulary Test-Revised scores were negligible (Beaujean & Osterlind, 2008), it is a verbal test that differs in many respects from Wechsler and Stanford-Binet tests. Wicherts et al. (2004) found that intelligence measures were not factorially invariant, such that the measures displayed differential patterns of gains and losses that were unexpected given each test’s common factor means. Taken together, these studies suggest that increases in IQ scores over time may be at least partly a result of changes in the measurement of intellectual functioning. Moreover, Dickinson and Hiscock (2010) reported that published norms for age-related changes in verbal and performance subtests do not take into account the Flynn effect. In comparisons of subtest scores from the WAIS-R and WAIS-III in 20-year-old and 70-year-old cohorts, the Flynn-corrected difference in Verbal IQ between 20-year-olds and 70-yearolds was 8.0 IQ points favoring the 70-year-olds (equivalent to 0.16 IQ points per year). In contrast, the younger group outscored the older group in Performance IQ by a margin of 9.5 IQ points (equivalent to 0.19 IQ points per year). These findings suggested that apparent age-related declines in Verbal IQ between the ages of 20 and 70 years are largely artifacts of the Flynn effect and that, even though age-related declines in Performance IQ are real declines, the magnitudes of those declines are amplified substantially by the Flynn effect.

Some studies have examined intercorrelations among subtests of IQ measures to determine the variance in IQ scores explained by g, with preliminary evidence suggesting that IQ gains have been associated with declines in measurement of g (Kane & Oakland, 2000; Te Nijenhuis & van der Flier, 2007). Flynn (2007), on the other hand, has discounted the association between g and increasing IQ scores, and a dissociation between g and the Flynn effects has been claimed by Rushton (2000). However, Raven’s Progressive Matrices, renowned for its g-loading, has demonstrated a rate of IQ gain of 7 points per decade, more than double the rate of the Flynn effect as manifested on WAIS, SB, and other multifactorial intellectual tests (Neisser, 1997).

What is Rising?

The theories highlighted above offer explanations for the Flynn effect but leave an important question unanswered: What exactly does the Flynn effect capture (i.e., what is rising)? Although much of the previous research on the Flynn effect has focused on the rise of mean IQ scores over time, studies distinguishing rates of gain among elements of IQ tests more readily answer the question of what is rising. Relative to scores produced by verbal tests, there have been greater gains in scores produced by nonverbal, performance-based measures like Raven’s Progressive Matrices (Neisser, 1997) and Wechsler performance subtests (Dickinson & Hiscock, 2011; Flynn, 1999). These types of tests are strongly associated with fluid intelligence, suggesting less of a rise in crystalized intelligence that reflects the influence of education, such as vocabulary. A notable exception is the increasing scores produced by the Wechsler verbal subtest Similarities (Flynn, 2007; Flynn & Weiss, 2007), although this subtest taps into elements of reasoning not required by the other subtests comprising the Wechsler Verbal IQ composite.

Dickens and Flynn (2001b) provided a framework for understanding the rise in more fluid versus crystallized cognitive abilities. They identified social multipliers as elements of the sociocultural milieu that contributed to rising IQ scores among successive cohorts of individuals. Flynn (2006b) highlighted two possible sociocultural contributions to the Flynn effect, one related to patterns of formal education and the other to the influence of science. Specifically, years of formal education increased in the years prior to World War II, whereas priorities in formal education shifted from rote learning to problem solving in the years following World War II. As time continued to pass, the value placed on problem solving in the workplace and leisure time spent on cognitively engaging activities continued to exert an effect on skills assessed by nonverbal, performance-based measures. The second sociocultural contributor, science, refers to the simultaneous rise in the influence of scientific reasoning and the abstract thinking and categorization required to perform well on nonverbal, performance-based measures.

The Current Study

The primary objective of this meta-analysis was to determine whether the Flynn effect could be replicated and more precisely estimated across a wide range of individually administered, multifactorial intelligence tests used at different ages and levels of performance. Answers to these research questions will assist in determining the confidence with which a correction for the Flynn effect can be applied across a variety of intelligence tests, ages, ability levels, and samples. By completing the meta-analysis, we also hoped to provide evidence evaluative of existing explanations for the Flynn effect, thus contributing to theory.

With the exceptions of the Flynn (1984a, 2009a) and Flynn and Weiss (2007) analyses of gains in IQ scores across successive versions of the Stanford-Binet and Wechsler intelligence tests, most research comparing IQ test scores has focused on correlations between two tests and/or average mean difference between two successive versions of the same test. This study will expand the literature on estimates of the Flynn effect by computing more precisely the magnitude of the effect over multiple versions of several widely-used, individually administered, multifactorial intelligence tests, viz., Kaufman, Stanford-Binet, and Wechsler tests and versions of the Differential Ability Scales, McCarthy Scales of Children’s Abilities, and the Woodcock-Johnson Tests of Cognitive Abilities. The data for these computations were obtained from validity studies conducted by test publishers or independent research teams. In addition to providing more precise weighted meta-analytic means, meta-analysis allows estimates of the standard error and evaluation of potential moderators.

This study deliberately focused on sources of heterogeneity (i.e., moderators) that could be readily identified through meta-analytic searches and that helped explain variability in estimates of the magnitude of the Flynn effect. Investigation of these moderators is needed to advance understanding of variables that might limit or promote confidence in applying a correction for the Flynn effect in high stakes decisions. Here the IQ tests that are used are variable in terms of test and normative basis, with the primary focus on the composite score. The tests are given to a broad age range and to people who vary in ability. It is not clear that the standard Flynn effect estimate can be applied among individuals of all ability levels and ages who took any of a number of individually-administered, multifactorial tests. In addition, there may be special circumstances related to test administration setting that might influence the numerical value of the Flynn effect. If the selected moderators (i.e., ability level, age, IQ tests administered, test administration setting, and test administration order) influence the estimate of the Flynn effect, the varying estimates will contribute to the tenability of the theories offered above for the existence and meaning of the Flynn effect.

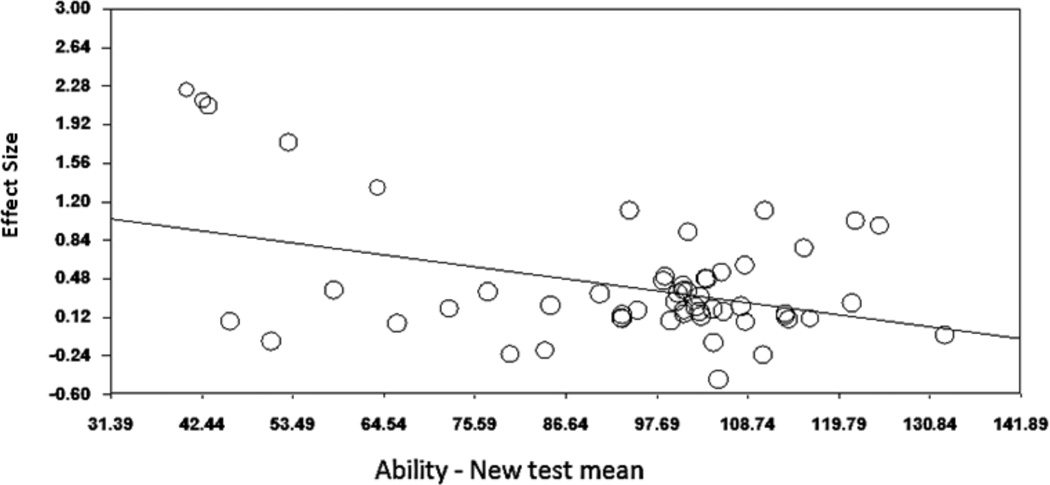
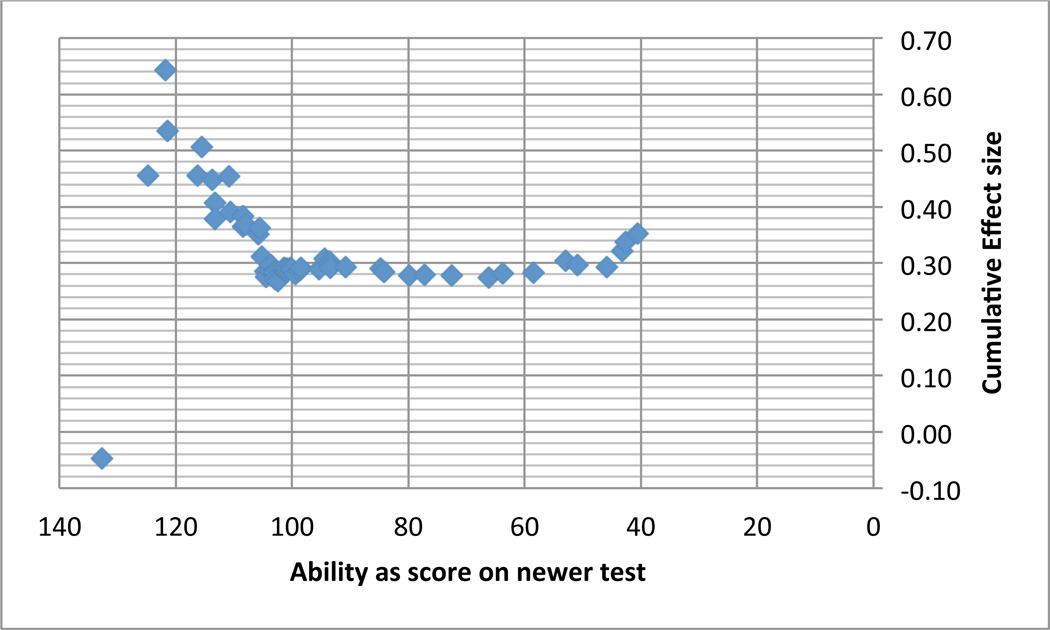
The evidence for influences of these moderators is mixed, with no clear directions. Recent evidence has suggested that middle and lower ability groups (IQ = 79–109) demonstrate the customary 0.31–0.37-point increase per year, whereas higher ability groups (IQ = 110+) demonstrate a minimal increase of 0.06–0.15 points per year (Zhou, Zhu, Weiss, & Pearson, 2010). Whereas some previous studies have supported this finding (e.g., Lynn & Hampson, 1986; Teasdale & Owen, 1989), others have not. Two studies found the opposite pattern (Graf & Hinton, 1994; Sanborn, Truscott, Phelps, & McDougal, 2003), and one study indicated smaller gains at intelligence levels both above and below average, with the highest gains evident in people at the lowest end of the ability spectrum (Spitz, 1989). Little research has been conducted to investigate the relation between age and gains in IQ score. Cross-sectional research has indicated no difference among young children, older children, and adults (Flynn, 1984b) and no difference among adult cohorts ranging in age from 35–80 years (Ronnlund & Nilsson, 2008).

Research on the Flynn effect has focused almost exclusively on the effect produced from administrations of the Stanford-Binet and Wechsler tests. This study expanded the scope by including a wider range of individually administered, largely multifactorial intelligence tests. Comparisons of older and more recently normed versions of the Stanford-Binet and Wechsler tests were conducted to facilitate comparisons with previous work and help determine if the Flynn effect has remained constant over time.

Another potential moderator pertains to study sample. Study data were collected by test publishers or independent researchers for validation purposes, or by mental health professionals for clinical decision-making purposes. Validation studies conducted by test publishers likely employed the most rigorous procedures with regard to sampling, selection of administrators, and adherence to administration and scoring protocols. However, the more homogenous samples examined in the research and clinical studies (e.g., children suspected of having an intellectual disability or juvenile delinquents) may produce results that are more generalizable to specific populations and permit comparison of Flynn effect values across those special populations.

Another set of moderators involves measurement issues, such as changes in subtest configuration and order effects. These issues were addressed by Kaufman (2010), who pointed out that changes in the instructions and content of specific Wechsler subtests (e.g., Similarities) could make comparing older and newer versions akin to comparing apples and oranges. However, other research has shown that estimates of the size of the Flynn effect based on changes in subtest scores yield values similar to estimates from the composite scores (Agbayani & Hiscock, 2013; Dickinson & Hiscock, 2010). Kaufman’s concern related to interpretations of the basis of the Flynn effect and not to its existence, and we did not pursue this question because it has been addressed in other studies (Dickinson & Hiscock, 2011). Subtest coding of a larger corpus of tests was difficult because the data were often not available. However, Kaufman also suggested that the Flynn effect could be the result of prior exposure when taking the newer version of an IQ test first and then transferring a learned response style to the older IQ test, thus receiving higher scores when the older test is given second. In order for order effects to occur, the interval between the administration of the new and old tests would have to be short enough for the examinee to demonstrate learning, which is often the case in studies comparing different versions of an IQ test, the basis for determination of the Flynn effect.

Although the Flynn effect has been well documented during the 20^th century, the meta-analytic method used during the current study is a novel approach to documenting this phenomenon. The method of the current study aligns with a key research proposal identified by Rodgers (1999) as important in advancing our understanding of the Flynn effect; viz., a formal meta-analysis. Although many of Rodgers’ (1999) proposals have since been implemented, there remains room for understanding the meaning of the Flynn effect, how the Flynn effect is reflected in batteries of tests over time, and how the Flynn effect manifests itself across subsamples defined by ability level or other characteristics.

Method

Inclusion and Exclusion Criteria

Studies identified from test manuals or peer-reviewed journals were included if they reported sample size and mean IQ score for each test administered; these variables were required for computation of the meta-analytic mean. All English-speaking participant populations from the United States and the United Kingdom were included. Variations in study design were acceptable. Administration of both tests must have occurred within one year of one another. Studies could have been conducted at any point prior to the completion date of the literature search in 2010.

We limited our primary investigation to comparisons between tests with greater than five years between norming periods, which is consistent with Flynn’s (2009) work. The rationale for this decision was that any difference in IQ scores from a short interval, even seemingly insignificant ones, would be magnified when converted to a value per decade (see Flynn, 2012). As a secondary analysis, we expanded our investigation to all comparisons between tests with at least one year between norming periods to assess whether our decision to limit our investigation to comparisons between tests with greater than five years between norming periods affected the results of the meta-analysis. We did not include comparisons between tests with one year or less between norming periods since years between norming periods served as the denominator of our effect size. A value of zero, representing no difference in years between norming periods, produced an error in the effect size estimate. Finally, we did not include single construct tests, such as the Peabody Picture Vocabulary Test or the Test of Nonverbal Intelligence. There may be other multifactorial tests to consider, but the 27 we chose represent the major IQ tests in use over the past few decades.

Search Strategies

Twenty-seven intelligence test manuals for multifactorial measures were obtained, one for each version of the Differential Ability Scales (Elliot, 1990; Elliot, 2007), Kaufman Adolescent and Adult Intelligence Test (Kaufman & Kaufman, 1993), Kaufman Assessment Battery for Children (Kaufman & Kaufman, 1983; Kaufman & Kaufman, 2004a), Kaufman Brief Intelligence Test (Kaufman & Kaufman, 1990; Kaufman & Kaufman, 2004b), McCarthy Scales of Children’s Abilities (McCarthy, 1972), Stanford-Binet Intelligence Scale (Roid, 2003; Terman & Merrill, 1937; Terman & Merrill, 1960; Terman & Merrill, 1973; Thorndike, Hagen, & Sattler, 1986), Wechsler Abbreviated Scale of Intelligence (Wechsler, 1999), Wechsler Adult Intelligence Scale (Wechsler, 1955; Wechsler, 1981; Wechsler, 1997; Wechsler, 2008), Wechsler Intelligence Scale for Children (Wechsler, 1949; Wechsler, 1974; Wechsler, 1991; Wechsler, 2003), Wechsler Preschool and Primary Scale of Intelligence (Wechsler, 1967; Wechsler, 1989; Wechsler, 2002), and Woodcock-Johnson Tests of Cognitive Ability (Woodcock & Johnson, 1977; Woodcock & Johnson, 1989; Woodcock, McGrew, & Mather, 2001).

Also, a systematic literature review was completed using PsycINFO®, crossing the keywords comparison, correlation, and validity with the full and abbreviated titles of the measures. The first author reviewed each study in full unless abstract review determined the study was not relevant (e.g., some test validation studies included comparisons between tests not under consideration in this meta-analysis). A formal search for unpublished studies was not undertaken; it was presumed that the results of test validation studies would provide important information irrespective of the findings and would therefore constitute publishable data.

Coding Procedures

The first author, who had prior training and experience in coding studies for meta-analyses, coded all of the studies in the current meta-analysis. Two undergraduate volunteers were trained by the first author, and each volunteer coded half the studies. Agreement between the first author and the volunteers on each variable was calculated for blocks of ten studies. These estimates ranged from 90.5–99.1% per block, with an average agreement of 95.8% per block. Discrepancies were resolved through discussion, during which the first author and volunteers referred to the original article. Discrepancies were commonly the result of a coder typo or failure of a coder to locate a particular value in an article.

Moderator Analyses

Moderators included ability level, age, test set, order of administration, and sample. Ability level was coded as the sample’s score on the most recently normed test, and age was coded as the sample’s age in months. Each comparison was assigned to a test set, as follows. First, due to Flynn’s focus on the Stanford-Binet and Wechsler tests, these tests were grouped together and were further separated into an old set and a modern set. The old set included comparisons of only Wechsler and Stanford-Binet tests normed before 1972, with the modern set representing versions normed since 1972. The latter set aligned with comparisons published in Flynn and Weiss (2007) and Flynn (2009). If a modern test was compared to an old test, the comparison was coded old. The Differential Ability Scales, Kaufman Adolescent and Adult Intelligence Test, and Woodcock-Johnson Tests of Cognitive Abilities were grouped together as non-Wechsler/Binet tests with modern standardization samples. The Kaufman Brief Intelligence Test and the Wechsler Abbreviated Scale of Intelligence were grouped together as screening tests. The Kaufman Assessment Battery for Children was separately analyzed due to its grounding in Luria’s model of information processing that addressed differences in simultaneous and sequential processing. Fourteen effects remained from the original set of 285 after sorting effects into these groupings. All of these comparisons contained the McCarthy Scales, but with multiple old and modern tests.

Order of administration was included as a moderator variable. Tests were frequently counterbalanced so that approximately half of the sample got each test first. However, in a substantial number of the studies, one test was uniformly given first. We coded these by the percentage of examinees given the old test first: 100 means that 100% of the examinees got the old test first; 0 means that all examinees got the new test first; 50 means that the tests were counterbalanced. In 7 of these effects, a different value was reported and these were rounded to 0, 0.50 or 100. For example, 14% (given the old test first) was rounded to 0, and 94% was rounded to 100.

Each comparison was also grouped by study sample. Standardization studies were completed during standardization and were reported in test manuals. Research studies appeared in peer-reviewed journals and examined comparisons among a small selection of intelligence tests. Clinical studies reported results from assessments completed of clinical samples, including determination of special education needs.

Statistical Methods

Effect size metric

Comprehensive Meta Analysis software (Borenstein, Hedges, Higgins, & Rothstein, 2005) was used for the core set of analyses. Specifically, we employed the module that requires input of an effect size and its variance for each study. Effects were coded as the difference between the old test mean and the new test mean. Positive effects reflect a positive Flynn effect with the score on the old test higher than the score on the new test despite being taken by the same individuals at approximately the same time. The effect size calculated from each study was the raw difference between the mean score on the old and new tests divided by the number of years between the norming dates of the two tests. This metric is directly interpretable as the estimated magnitude of the Flynn effect per year. Since the scales used by all of the tests were virtually the same (M = 100, SD = 15 or 16), no further standardization (such as dividing by population standard deviation [SD]) was required (Borenstein, Hedges, Higgins, & Rothstein, 2009). The actual SD for each test was used in computing the variance of the effects.

Effect size weighting

The variance for each effect is required for computation of the weight given to each effect in the overall analysis. The weight is the inverse of the variance, so studies with the smallest variance are given the most weight. Small variance (high precision) for an effect is achieved via (a) large Ns, (b) high reliabilities for both tests and high content overlap between tests which are jointly reflected in the correlation between the tests, and (c) long intervals between the norming periods of the two tests. The formula (Borenstein, Hedges, Higgins, & Rothstein, 2009) used for the variance of typical pretest-posttest effects in meta-analysis is:

$$\text{Variance}=\frac{S{D}_{\mathit{\text{New}}}^2+S{D}_{\mathit{\text{Old}}}^2-2rS{D}_{\mathit{\text{New}}}S{D}_{\mathit{\text{Old}}}}{N}$$ (1)

Where SD²_New is the variance of the more recently normed test, SD²_Old is the variance of the less recently normed test, r is the reported correlation between the two tests, and N is the total sample size. In the numerator, actual reported correlations were used when available. For 54 of the 285 studies, no correlation was reported. In these cases, if there were other studies that compared the same two tests, the correlations from the other studies were converted to Fisher’s z. These were then averaged and converted back to a correlation and used in place of the missing value. If no other studies compared the same two tests, the mean correlation for the entire set of studies was computed and substituted in for the missing value. This occurred for two study results. The mean correlation for each pair of tests was also retained and used in a parallel analysis to determine the impact of using the sample-specific correlation rather than a population correlation in the estimator of the effect variance.

To allow for the differential precision in effects due to the years between norming periods of the two tests being compared, we adapted a formula from Raudenbush and Xiao-Feng (2001) that allows calculation of the change in variance as a function of the change in duration in years of the period between the norming of the two tests, holding number of time points constant. Using D to represent a duration of 1 year, D’ to represent a different duration, either longer or shorter, and ω=D’/D to represent the factor of increase or decrease from one year, then the proportion of the variances is equal to:

$$\frac{\mathrm{V}\prime }{\mathrm{V}}=\frac{1}{{\mathrm{\omega }}^2}$$ (2)

In other words, the variance (V’) for an effect with a 5 year duration between norming periods will be 1/25^th the size of the variance (V) of an effect with a one year duration between norming periods, all other things being equal. Thus, the variance we entered into the CMA software for each effect size was:

$$\text{Variance}=\frac{S{D}_{\mathit{\text{New}}}^2+S{D}_{\mathit{\text{Old}}}^2-2rS{D}_{\mathit{\text{New}}}S{D}_{\mathit{\text{Old}}}}{N{\mathrm{\omega }}^2}$$ (3)

The numerator of the above formula is the variance of the difference between the two tests being compared. The denominator adjusts this variance by the sample size (N) and by the duration in years of the period between the norming of the two tests.

Credibility intervals

In a random effects model, the true variance of effects is estimated. The standard deviation of this distribution is represented by Tau [τ]. Tau is used to form a credibility interval around the mean effect, capturing 95% of the distribution of true effects by extending out 1.96τ from the mean in both positive and negative directions. The credibility interval acknowledges that there is a distribution of true effects rather than one true effect. In interpreting the credibility interval, it is helpful to consider width as well as location. Even a distribution of true effects that is centered near 0 (where the mean effect might not be significant) may contain many members that might be meaningfully large in either direction. Moderator analysis may be used to try to find subsets of effects within this distribution, to narrow the uncertainty about how large the effect might be in a given situation; however, in the case of true random effects, each causal variable might explain a very small portion of the variance and moderator analysis might not improve prediction substantially.

Selection of random effects model

A random effects analytic model was employed because the studies were not strict replications of each other, in which case it would make sense to expect a single underlying fixed effect. Rather, the studies varied in multiple ways, each of which was expected to have some impact on the observed Flynn effect. These factors include, but are not limited to (a) the specific test pair being compared, (b) the unique population being tested, (c) the age of the sample (which was not always reported quantitatively), (d) the interval between the presentation of the old and new test, (e) the order of presentation of the tests, (f) unusual administration practices (e.g., Spruill, 1988), and (g) interactions among these factors. The result of these multiple causes is a distribution of true effects, rather than a single effect.

In a random effects model, the mean effect is ultimately interpreted as the mean of a distribution of true population effects. Additionally, in a random effects model, the variance of the effects has two variance components. One is due to the true variance in population effects and the second is due to sampling variance around the population mean effect. The result is that the weight given each study is a function of both within-study precision due to sample size and between-study variability. Sample size thus has less effect in the precision of each study. Large sample size studies are given less weight than they would have been in a fixed effects study, and studies with smaller samples are given more weight (Borenstein et al., 2009).

Heterogeneity in effect sizes

Heterogeneity describes the degree to which effect sizes vary between studies. The Q statistic is employed to capture the significance of this variance and is calculated by summing the squared differences between individual study effect sizes and the mean effect size. It is distributed as a chi-square statistic with k-1 degrees of freedom, where k is the number of studies. In addition, I² is employed to capture the extent to which detected heterogeneity is due not to chance but to true, identifiable variation between studies. I² is calculated:

$$I^2=(Q-df)/Q$$ (4)

and once multiplied by 100 is directly interpretable as the proportion of variance due to true heterogeneity.

Publication bias

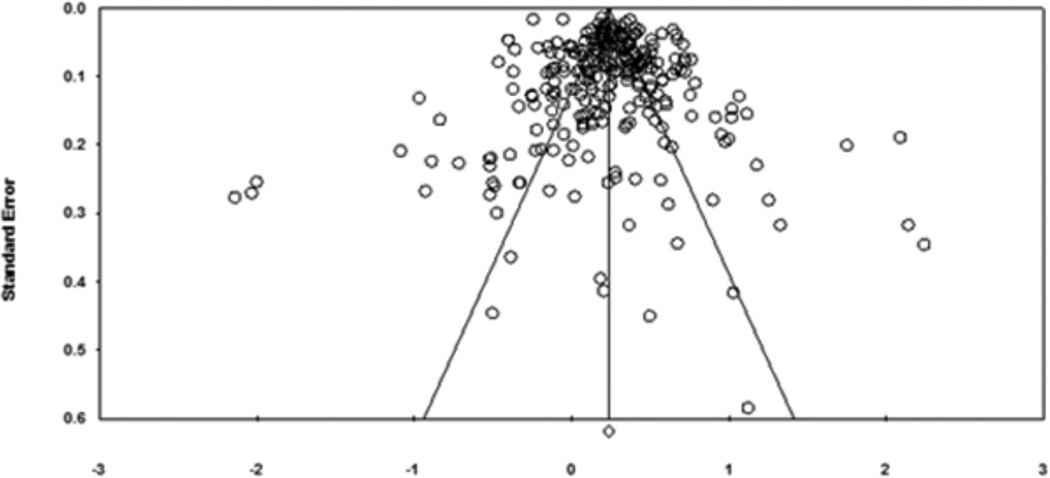
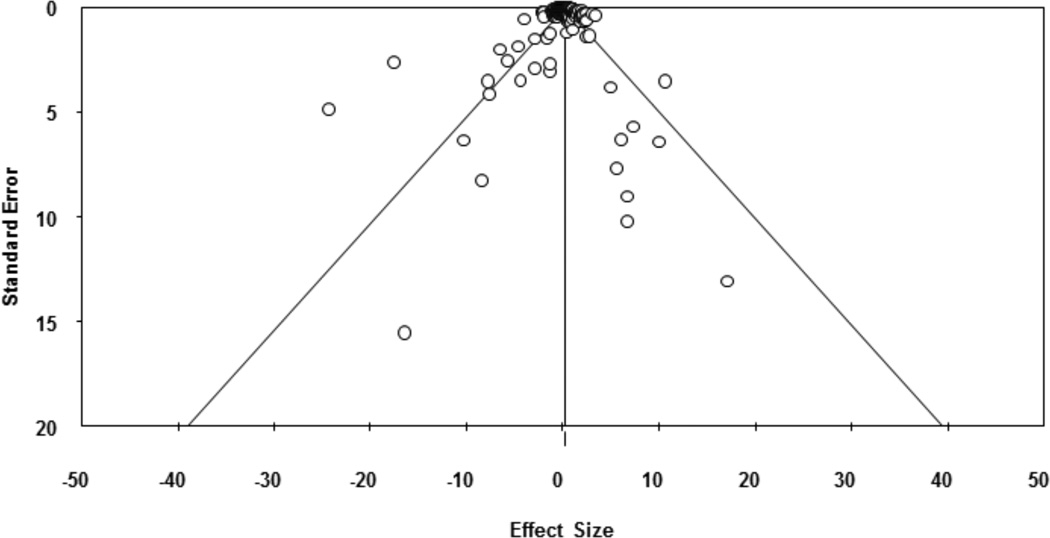
We did not expect to find evidence for publication bias in this meta-analysis. The descriptive data collected from each study in the form of sample sizes, means, and correlations between tests is not typically the type of data that is subject to tests of significance and thus would not be a direct cause of failure to publish due to non-significance. Additionally, many of the effects were gleaned from the technical manuals of the tests being compared where no publication bias is expected. However, we did evaluate the distributions of effects within each portion of our analysis via funnel plots.

Results

Citations

The literature review produced a total of 4,383 articles. This total does not reflect unique articles, since each article would often appear in multiple keyword searches. One hundred and fifty-four empirical studies and 27 test manuals met inclusion criteria, from which 378 comparisons were extracted, 285 of which were normed more than 5 years apart. The chronological range of the Flynn effect data collected was from 1951 upon publication of Weider, Noller, and Schramm’s (1951) comparison study of the WISC and SB to 2010, the year in which the literature review was completed. Table 1 shows the effect size produced by each of the 378 comparisons and includes information pertaining to sample size and age in months.

Table 1.

Sample Size, Sample Age, Tests Administered, and Effect Sizes by Study

	Source	N	Agea	Newer Test	Older Test	Effect size
			Modern ≥ 5b
1	Bower & Hayes, 1995	26	132.88	SB4c	SB 72d	0.08
2	Carvajal & Weyand, 1986	23	109.5	SB4	WISC-Re	0.13
3	Carvajal et al., 1987	32	227	SB4	WAIS-Rf	0.37
4	Clark et al., 1987	47	63	SB4	SB 72	0.07
5	Doll & Boren, 1993	24	114	WISC-IIIg	WISC-R	0.35
6	Gordon et al., 2010	17	194	WISC-IVh	WAIS-IIIi	1.75
7	Gunter et al., 1995	16	132	WISC-III	WISC-R	−0.19
8	Krohn & Lamp, 1989	89	59	SB4	SB 72	0.11
9	Lamp & Krohn, 2001	89	59	SB4	SB 72	0.10
10	Nelson & Dacey, 1999	42	248.04	SB4	WAIS-R	2.09
11	Quereshi & Seitz, 1994	72	75.1	WPPSI-Rj	WISC-R	0.34
12	Quereshi et al., 1989	36	197.9	WAIS-R	WISC-R	0.1
13	Quereshi et al., 1989	36	197.9	WAIS-R	WISC-R	1.11
14	Quereshi et al., 1989	36	197.05	WAIS-R	WISC-R	0.18
15	Quereshi et al., 1989	36	197.05	WAIS-R	WISC-R	1.11
16	Robinson & Nagle, 1992	75	111	SB4	WISC-R	0.25
17	Robinson et al., 1990	28	30	SB4	SB 72	0.97
18	Roid, 2003	87	744	SB5k	WAIS-III	0.91
19	Roid, 2003	66	132	SB5	WISC-III	0.41
20	Roid, 2003	71	48	SB5	WPPSI-R	−0.46
21	Roid, 2003	104	108	SB5	SB4	0.22
22	Roid, 2003	80	84	SB5	SB L-Ml	0.12
23	Rothlisberg, 1987	32	93.19	SB4	WISC-R	0.53
24	Sabatino & Spangler, 1995	51	163.2	WISC-III	WISC-R	−0.04
25	Sandoval et al., 1988	30	197.5	WAIS-R	WISC-R	0.18
26	Sevier & Bain, 1994	35	110	WISC-III	WISC-R	0.76
27	Spruill, 1991	32	․	SB4	WAIS-R	2.24
28	Spruill, 1991	38	․	SB4	WAIS-R	2.14
29	Thompson & Sota, 1998	23	196	WISC-III	WAIS-R	0.60
30	Thompson & Sota, 1998	23	196	WISC-III	WAIS-R	−0.23
31	Thorndike et al., 1986	21	234	SB4	WAIS-R	1.32
32	Thorndike et al., 1986	47	233	SB4	WAIS-R	0.5
33	Thorndike et al., 1986	205	113	SB4	WISC-R	0.21
34	Thorndike et al., 1986	19	155	SB4	WISC-R	0.10
35	Thorndike et al., 1986	90	132	SB4	WISC-R	0.23
36	Thorndike et al., 1986	61	167	SB4	WISC-R	0.06
37	Thorndike et al., 1986	139	83	SB4	SB 72	0.17
38	Thorndike et al., 1986	82	88	SB4	SB 72	1.01
39	Thorndike et al., 1986	14	100	SB4	SB 72	−0.22
40	Thorndike et al., 1986	22	143	SB4	SB 72	−0.10
41	Urbina & Clayton, 1991	50	79	WPPSI-R	WISC-R	0.48
42	Wechsler, 1981	80	192	WAIS-R	WISC-R	0.15
43	Wechsler, 1989	50	79	WPPSI-R	WISC-R	0.47
44	Wechsler, 1991	189	192	WISC-III	WAIS-R	0.36
45	Wechsler, 1991	206	132	WISC-III	WISC-R	0.31
46	Wechsler, 1997	184	192	WAIS-III	WISC-III	−0.11
47	Wechsler, 1997	24	219.6	WAIS-III	WISC-R	0.33
48	Wechsler, 1997	26	343.2	WAIS-III	SB4	0.15
49	Wechsler, 1997	192	522	WAIS-III	WAIS-R	0.17
50	Wechsler, 1997	88	583.2	WAIS-III	WAIS-R	0.14
51	Wechsler, 2002	176	60	WPPSI-IIIm	WPPSI-R	0.08
52	Wechsler, 2003	183	192	WISC-IV	WAIS-III	0.45
53	Wechsler, 2003	233	132	WISC-IV	WISC-III	0.19
54	Wechsler, 2008	238	632.4	WAIS-IVn	WAIS-III	0.26
55	Wechsler, 2008	24	386.4	WAIS-IV	WAIS-III	0.37
56	Wechsler, 2008	24	348	WAIS-IV	WAIS-III	0.2
			Other ≥ 5o
57	Appelbaum & Tuma, 1977	20	121	WISC-R	WISCp	0.07
58	Appelbaum & Tuma, 1977	20	120	WISC-R	WISC	0.15
59	Arinoldo, 1982	20	57	MSCAq	WPPSIr	0.20
60	Arnold & Wagner, 1955	50	102	WISC	SB 32s	0.07
61	Axelrod & Naugle, 1998	200	519.6	KBITt	WAIS-R	−0.4
62	Barratt & Baumgarten, 1957	30	126	WISC	SB 32	0.58
63	Barratt & Baumgarten, 1957	30	126	WISC	SB 32	0.08
64	Bradway & Thompson, 1962	111	354	WAISu	SB 32	0.66
65	Brengelmann & Renny, 1961	75	442.92	WAIS	SB 32	−0.35
66	Brooks, 1977	30	96	WISC-R	WISC	0.29
67	Brooks, 1977	30	96	SB 72	WISC	0.37
68	Byrd & Buckhalt, 1991	46	149	DASv	WISC-R	0.12
69	Carvajal et al., 1988	21	69	SB4	MSCA	−0.1
70	Carvajal et al., 1988	20	66	SB4	WPPSI	0.05
71	Chelune et al., 1987	43	576	WAIS-R	WAIS	0.40
72	Cohen & Collier, 1952	51	89	WISC	SB 32	0.32
73	Covin, 1977	30	102	WISC-R	WISC	−0.00
74	Craft & Kronenberger, 1979	15	196.44	WISC-R	WAIS	0.72
75	Craft & Kronenberger, 1979	15	196.8	WISC-R	WAIS	0.54
76	Davis, 1975	53	69	MSCA	SB 60w	0.57
77	Edwards & Klein, 1984	19	451.2	WAIS-R	WAIS	0.13
78	Edwards & Klein, 1984	19	451.2	WAIS-R	WAIS	0.37
79	Eisenstein & Engelhart, 1997	64	500.4	KBIT	WAIS-R	−0.25
80	Elliot, 1990	23	54	WPPSI-R	K-ABCx	0.5
81	Elliot, 1990	49	41.5	DAS	MSCA	0.42
82	Elliot, 1990	40	42.5	DAS	MSCA	0.45
83	Elliot, 1990	66	110	DAS	WISC-R	0.50
84	Elliot, 1990	60	180	DAS	WISC-R	0.35
85	Elliot, 1990	23	54	DAS	K-ABC	0.67
86	Elliot, 1990	27	72	DAS	K-ABC	1.25
87	Faust & Hollingsworth, 1991	33	53.9	WPPSI-R	MSCA	0.07
88	Field & Sisley, 1986	17	360	WAIS-R	WAIS	0.22
89	Field & Sisley, 1986	25	360	WAIS-R	WAIS	0.25
90	Fourqurean, 1987	42	116	K-ABC	WISC-R	−0.71
91	Frandsen & Higginson, 1951	54	116	WISC	SB 32	0.21
92	Gehman & Matyas, 1956	60	182	WISC	SB 32	−0.10
93	Gehman & Matyas, 1956	60	133	WISC	SB 32	−0.12
94	Gerken & Hodapp, 1992	16	54	WPPSI-R	SB 60	0.08
95	Giannell & Freeburne, 1963	38	218.88	WAIS	SB 32	0.55
96	Giannell & Freeburne, 1963	36	219.96	WAIS	SB 32	0.50
97	Giannell & Freeburne, 1963	35	224.28	WAIS	SB 32	0.35
98	Hamm et al., 1976	22	121.68	WISC-R	WISC	0.32
99	Hamm et al., 1976	26	153.73	WISC-R	WISC	0.29
100	Hannon & Kicklighter, 1970	13	192	WAIS	WISC	−0.04
101	Hannon & Kicklighter, 1970	13	192	WAIS	WISC	−2.03
102	Hannon & Kicklighter, 1970	32	192	WAIS	WISC	0.95
103	Hannon & Kicklighter, 1970	33	192	WAIS	WISC	−0.50
104	Hannon & Kicklighter, 1970	11	192	WAIS	WISC	1.12
105	Hannon & Kicklighter, 1970	18	192	WAIS	WISC	1.03
106	Harrington et al., 1992	10	48	WPPSI-R	WJTCAy	−0.66
107	Harrington et al., 1992	10	60	WPPSI-R	WJTCA	−0.16
108	Hartlage & Boone, 1977	42	126	WISC-R	WISC	0.20
109	Hartwig et al., 1987	30	135.6	SB4	SB 60	−0.05
110	Hays et al., 2002	85	408	WASI	KBIT	0.22
111	Holland, 1953	23	․	WISC	SB 32	0.10
112	Holland, 1953	29	․	WISC	SB 32	0.10
113	Jones, 1962	80	96	WISC	SB 32	0.54
114	Jones, 1962	80	108	WISC	SB 32	0.46
115	Jones, 1962	80	120	WISC	SB 32	0.38
116	Kangas & Bradway, 1971	48	498	SB 60	WAIS	−2
117	Kaplan et al., 1991	30	57	WPPSI-R	WPPSI	0.36
118	Karr et al., 1992	21	69	SB4	MSCA	−0.17
119	Karr et al., 1993	32	63.6	WPPSI-R	MSCA	0.07
120	Kaufman & Kaufman, 1990	64	257	KBIT	WAIS-R	−0.11
121	Kaufman & Kaufman, 1990	41	66	KBIT	K-ABC	−0.13
122	Kaufman & Kaufman, 1990	35	128	KBIT	WISC-R	0.35
123	Kaufman & Kaufman, 1990	70	100	KBIT	K-ABC	0.07
124	Kaufman & Kaufman, 1990	39	136	KBIT	K-ABC	−0.48
125	Kaufman & Kaufman, 1993	118	156	KAIT	WISC-R	0.23
126	Kaufman & Kaufman, 1993	71	208.8	KAIT	WAIS-R	0.14
127	Kaufman & Kaufman, 1993	108	312	KAIT	WAIS-R	0.21
128	Kaufman & Kaufman, 1993	90	494.4	KAIT	WAIS-R	0.47
129	Kaufman & Kaufman, 1993	74	747.6	KAIT	WAIS-R	0.25
130	Kaufman & Kaufman, 1993	124	135.6	KAIT	K-ABC	0.47
131	Kaufman & Kaufman, 2004b	54	68	KBIT-IIz	K-BIT	0.10
132	Kaufman & Kaufman, 2004a	48	120	K-ABC-IIaa	K-ABC	0.30
133	Kaufman & Kaufman, 2004a	119	126	K-ABC-II	WISC-III	0.09
134	Kaufman & Kaufman, 2004a	29	174	K-ABC-II	KAITbb	0.13
135	Kaufman & Kaufman, 2004b	53	135	KBIT-II	K-BIT	0.24
136	Kaufman & Kaufman, 2004b	74	383	KBIT-II	K-BIT	0.16
137	Kaufman & Kaufman, 2004b	43	122	KBIT-II	WISC-III	0.24
138	Kaufman & Kaufman, 2004b	67	384	KBIT-II	WAIS-III	0.78
139	King & Smith, 1972	24	72	WPPSI	WISC	−0.15
140	King & Smith, 1972	24	72	SB 60	WISC	−0.51
141	Klanderman et al., 1985	41	102	K-ABC	SB 72	0.56
142	Klanderman et al., 1985	41	102	K-ABC	WISC-R	0.40
143	Klinge et al., 1976	16	169.32	WISC-R	WISC	−0.12
144	Klinge et al., 1976	16	169.32	WISC-R	WISC	0.40
145	Krohn et al., 1988	38	51	K-ABC	SB 72	−0.32
146	Krohn & Lamp, 1989	89	59	K-ABC	SB 72	−0.12
147	Krugman et al., 1951	38	60	WISC	SB 32	0.72
148	Krugman et al., 1951	20	174	WISC	SB 32	0.24
149	Krugman et al., 1951	38	72	WISC	SB 32	0.64
150	Krugman et al., 1951	43	84	WISC	SB 32	0.25
151	Krugman et al., 1951	44	96	WISC	SB 32	0.39
152	Krugman et al., 1951	31	108	WISC	SB 32	0.66
153	Krugman et al., 1951	29	120	WISC	SB 32	0.36
154	Krugman et al., 1951	37	132	WISC	SB 32	0.42
155	Krugman et al., 1951	22	144	WISC	SB 32	0.42
156	Krugman et al., 1951	30	156	WISC	SB 32	0.42
157	Kureth et al., 1952	50	60	WISC	SB 32	0.72
158	Kureth et al., 1952	50	72	WISC	SB 32	0.36
159	Lamp & Krohn, 2001	89	59	K-ABC	SB 72	−0.11
160	Larrabee & Holroyd, 1976	24	129	WISC-R	WISC	0.25
161	Larrabee & Holroyd, 1976	14	129	WISC-R	WISC	0.50
162	Levinson, 1959	57	65.54	WISC	SB 32	0.76
163	Levinson, 1959	60	66.65	WISC	SB 32	0.66
164	Levinson, 1960	117	66.1	WISC	SB 32	0.71
165	Lippold & Claiborn, 1983	30	619.56	WAIS-R	WAIS	0.34
166	McCarthy, 1972	35	75	MSCA	SB 60	1.02
167	McCarthy, 1972	35	75	MSCA	WPPSI	0.36
168	McGinley, 1981	12	141	WISC-R	WISC	0.17
169	McGinley, 1981	9	141	WISC-R	WISC	0.37
170	McKerracher & Scott, 1966	31	384	SB 60	WAIS	0.64
171	Milrod & Rescorla, 1991	50	59	WPPSI-R	WPPSI	0.38
172	Milrod & Rescorla, 1991	30	59	WPPSI-R	WPPSI	0.05
173	Mishra & Brown, 1983	88	359.76	WAIS-R	WAIS	0.19
174	Mitchell et al., 1986	35	․	WAIS-R	WAIS	0.15
175	Munford, 1978	10	141	WISC-R	WISC	0.04
176	Munford, 1978	10	141	WISC-R	WISC	−0.36
177	Munford & Munoz, 1980	11	150.5	WISC-R	WISC	−0.07
178	Munford & Munoz, 1980	9	150.5	WISC-R	WISC	0.34
179	Nagle & Lazarus, 1979	30	197.5	WISC-R	WAIS	0.69
180	Naglieri, 1984	35	105	K-ABC	WISC-R	−0.92
181	Naglieri, 1984	33	105	K-ABC	WISC-R	0.59
182	Naglieri, 1985	37	117	K-ABC	WISC-R	−0.83
183	Naglieri, 1985	51	91	K-ABC	MSCA	−0.11
184	Naglieri & Jensen, 1987	86	128.4	K-ABC	WISC-R	0.43
185	Naglieri & Jensen, 1987	86	129.6	K-ABC	WISC-R	0.08
186	Naugle et al., 1993	200	519.6	KBIT	WAIS-R	−0.39
187	Oakland et al., 1971	24	72	SB 60	WISC	−0.52
188	Oakland et al., 1971	24	74	WPPSI	WISC	0.21
189	Oakland et al., 1971	24	72	WPPSI	WISC	−0.15
190	Oakland et al., 1971	24	74	SB 60	WISC	0.02
191	Obrzut et al., 1984	19	110.06	K-ABC	WISC-R	0.28
192	Obrzut et al., 1984	13	111.06	K-ABC	WISC-R	−0.47
193	Obrzut et al., 1987	29	114.96	K-ABC	SB 72	−0.38
194	Obrzut et al., 1987	29	114.96	K-ABC	WISC-R	−0.88
195	Phelps et al., 1993	40	108	WISC-III	K-ABC	1.00
196	Phillips et al., 1978	60	73.92	MSCA	WPPSI	1.17
197	Pommer, 1986	56	87.86	K-ABC	WISC-R	−1.08
198	Prewett, 1992	40	189	KBIT	WISC-R	0.02
199	Prifitera & Ryan, 1983	32	529.08	WAIS-R	WAIS	0.31
200	Quereshi, 1968	124	180.1	WAIS	WISC	0.6
201	Quereshi & Miller, 1970	72	208.65	WAIS	WISC	0.49
202	Quereshi & McIntire, 1984	24	74.5	WPPSI	WISC	0
203	Quereshi & McIntire, 1984	24	74.5	WPPSI	WISC	0.50
204	Quereshi & McIntire, 1984	24	74.5	WPSSI	WISC	0.16
205	Quereshi & McIntire, 1984	24	74.5	WISC-R	WISC	−0.14
206	Quereshi & McIntire, 1984	24	74.5	WISC-R	WISC	0.25
207	Quereshi & McIntire, 1984	24	74.5	WISC-R	WISC	0.18
208	Quereshi & McIntire, 1984	24	74.5	WISC-R	WPPSI	−0.49
209	Quereshi & McIntire, 1984	24	74.5	WISC-R	WPPSI	−0.33
210	Quereshi & McIntire, 1984	24	74.5	WISC-R	WPPSI	0.23
211	Quereshi & Ostrowski, 1985	72	230.9	WAIS-R	WAIS	0.15
212	Quereshi & Erstad, 1990	36	891.6	WAIS-R	WAIS	0.64
213	Quereshi & Erstad, 1990	36	891.6	WAIS-R	WAIS	0.43
214	Quereshi & Erstad, 1990	18	1032	WAIS-R	WAIS	0.67
215	Quereshi & Erstad, 1990	27	906	WAIS-R	WAIS	0.57
216	Quereshi & Erstad, 1990	27	786	WAIS-R	WAIS	0.41
217	Quereshi & Seitz, 1994	72	75.1	WPPSI-R	WPPSI	0.40
218	Quereshi & Seitz, 1994	72	75.1	WISC-R	WPPSI	0.53
219	Rabourn, 1983	52	308.4	WAIS-R	WAIS	0.27
220	Reilly et al., 1985	26	84	WJTCA	MSCA	−0.05
221	Reynolds & Hartlage, 1979	66	152.4	WISC-R	WISC	0.18
222	Rohrs & Haworth, 1962	46	149.88	SB 60	WISC	−0.33
223	Ross & Morledge, 1967	30	192	WAIS	WISC	−0.36
224	Rowe, 1977	20	170.5	WISC-R	WISC	0.016
225	Rowe, 1977	24	170.5	WISC-R	WISC	0.34
226	Rust & Yates, 1997	67	102	WISC-III	K-ABC	0.01
227	Schwarting, 1976	58	126	WISC-R	WISC	0.30
228	Sewell, 1977	35	62.29	SB 72	WPPSI	0.61
229	Shahim, 1992	40	74.4	WISC-R	WPPSI	−0.22
230	Sherrets & Quattrocchi, 1979	13	141.6	WISC-R	WISC	0.05
231	Sherrets & Quattrocchi, 1979	15	141.6	WISC-R	WISC	0.20
232	Simon & Clopton, 1984	29	354	WAIS-R	WAIS	−0.08
233	Simpson, 1970	120	192	WAIS	WISC	−0.96
234	Skuy et al., 2000	21	114	K-ABC	WISC-R	−2.13
235	Skuy et al., 2000	35	100.8	K-ABC	WISC-R	−0.38
236	Smith, 1983	35	247.2	WAIS-R	WAIS	−0.21
237	Smith, 1983	35	247.2	WAIS-R	WAIS	0.51
238	Solly, 1977	12	124	WISC-R	WISC	0.50
239	Solly, 1977	12	124	WISC-R	WISC	0.43
240	Spruill & Beck, 1988	23	306	WAIS-R	WAIS	0.37
241	Spruill & Beck, 1988	35	306	WAIS-R	WAIS	0.19
242	Spruill & Beck, 1988	25	306	WAIS-R	WAIS	−0.05
243	Spruill & Beck, 1988	25	306	WAIS-R	WAIS	−0.24
244	Stokes et al., 1978	59	147	WISC-R	WISC	0.10
245	Swerdlik, 1978	100	108	WISC-R	WISC	0.23
246	Swerdlik, 1978	64	163.2	WISC-R	WISC	0.20
247	Templer et al., 1985	15	347.16	WAIS-R	SB 60	0.75
248	Thorndike et al., 1986	75	66	SB4	WPPSI	0.24
249	Triggs & Cartee, 1953	46	60	WISC	SB 32	1.06
250	Tuma et al., 1978	9	119	WISC-R	WISC	0.12
251	Tuma et al., 1978	9	119	WISC-R	WISC	0.29
252	Tuma et al., 1978	9	123	WISC-R	WISC	−0.04
253	Tuma et al., 1978	9	123	WISC-R	WISC	0.27
254	Urbina et al., 1982	68	505.92	WAIS-R	WAIS	0.21
255	Valencia & Rothwell, 1984	39	54.9	MSCA	WPPSI	0.18
256	Valencia, 1984	42	59.5	K-ABC	WPPSI	−0.10
257	Walters & Weaver, 2003	20	278.4	WAIS-III	KBIT	−0.51
258	Wechsler, 1955	52	252	WAIS	SB 32	0.23
259	Wechsler, 1974	40	203	WISC-R	WAIS	0.33
260	Wechsler, 1974	50	72	WISC-R	WPPSI	0.34
261	Wechsler, 1981	72	474	WAIS-R	WAIS	0.30
262	Wechsler, 1989	61	63.5	WPPSI-R	WPPSI	0.50
263	Wechsler, 1989	83	63.5	WPPSI-R	WPPSI	0.20
264	Wechsler, 1989	93	62.5	WPPSI-R	MSCA	0.14
265	Wechsler, 1989	59	61	WPPSI-R	K-ABC	0.9
266	Wechsler, 1999	176	137.52	WASI	WISC-III	0.02
267	Weider et al., 1951	44	77.5	WISC	SB 32	0.47
268	Weider et al., 1951	62	119.5	WISC	SB 32	0.00
269	Weiner & Kaufman, 1979	46	110	WISC-R	WISC	0.32
270	Wheaton et al., 1980	25	119.76	WISC-R	WISC	−0.01
271	Wheaton et al., 1980	25	116.16	WISC-R	WISC	0.36
272	Whitworth & Gibbons, 1986	25	252	WAIS-R	WAIS	0.18
273	Whitworth & Gibbons, 1986	25	252	WAIS-R	WAIS	0.30
274	Whitworth & Gibbons, 1986	25	252	WAIS-R	WAIS	0.21
275	Whitworth & Chrisman, 1987	30	58	K-ABC	WPPSI	0.35
276	Whitworth & Chrisman, 1987	30	58	K-ABC	WPPSI	0.13
277	Woodcock et al., 2001	150	117.5	WJTCA-III	WISC-III	0.57
278	Woodcock et al., 2001	122	120.6	WJTCA-III	DAS	0.42
279	Yater et al., 1975	20	80.5	WPPSI	WISC	−0.11
280	Yater et al., 1975	20	63.45	WPPSI	WISC	0.23
281	Yater et al., 1975	20	68.15	WPPSI	WISC	−0.24
282	Zimmerman & Woo-Sam, 1974	22	72	SB 72	WPPSI	−0.01
283	Zimmerman & Woo-Sam, 1974	22	66	SB 72	WPPSI	−0.5
284	Zins & Barnett, 1984	40	111	K-ABC	SB 72	0.28
285	Zins & Barnett, 1984	40	111	K-ABC	WISC-R	0.58
			Modern < 5cc
286	Brooks, 1977	30	96	WISC	SB 72	−7.76
287	Carvajal et al., 1991	51	68.4	WPPSI	SB4	2.36
288	Carvajal et al., 1993	32	123	WISC-III	SB4	−0.74
289	Klanderman et al., 1985	41	102	WISC-R	SB 72	6.16
290	Lavin, 1996	40	127.2	WISC-III	SB4	0.28
291	Lukens & Hurrell, 1996	31	161	WISC-III	SB4	2.05
292	McCrowell & Nagle, 1994	30	60	WPPSI-R	SB4	0.63
293	Obrzut et al., 1987	29	114.96	WISC-R	SB 72	17.2
294	Prewett & Matavich, 1994	73	116	WISC-III	SB4	2.23
295	Rust & Lindstrom, 1996	57	111.6	WISC-III	SB4	−0.37
296	Sewell & Manni, 1977	33	84	WISC-R	SB 72	7.4
297	Sewell & Manni, 1977	73	144	WISC-R	SB 72	5.08
298	Simpson et al., 2002	20	108	WISC-III	SB4	1.86
299	Simpson et al., 2002	20	111	WISC-III	SB4	0.88
300	Wechsler, 1974	29	114	WISC-R	SB 72	6.8
301	Wechsler, 1974	27	150	WISC-R	SB 72	6.8
302	Wechsler, 1974	29	198	WISC-R	SB 72	−8.4
303	Wechsler, 1974	33	72	WISC-R	SB 72	10
304	Wechsler, 1989	115	70	WPPSI-R	SB4	0.69
305	Wechsler, 1991	188	72	WISC-III	WPPSI-R	−4
306	Wechsler, 2003	254	132	WISC-IV	WASI	0.85
307	Wechsler, 2008	141	198	WAIS-IV	WISC-IV	0.28
308	Zins & Barnett, 1984	40	111	WISC-R	SB 72	−10.24
			Other < 5dd
309	Arffa et al., 1984	60	55	WJTCA	SB 72	−0.86
310	Arinoldo, 1982	20	93	WISC-R	MSCA	−6.5
311	Axelrod, 2002	72	644.4	WASI	WAIS-III	−0.98
312	Barclay, 1969	50	63.84	WPPSI	SB 60	1.51
313	Bracken et al., 1984	99	143	WJTCA	WISC-R	2.14
314	Bracken et al., 1984	37	143	WJTCA	WISC-R	1.44
315	Coleman & Harmer, 1985	54	108	WJTCA	WISC-R	1.32
316	Davis, 1975	53	69	SB 72	MSCA	0.4
317	Davis & Walker, 1977	51	97	WISC-R	MSCA	−1.6
318	Dumont et al., 2000	81	148	DAS	WJTCA-Ree	−2.8
319	Elliot, 1990	62	63	DAS	WPPSI-R	10.8
320	Elliot, 1990	23	54	DAS	WPPSI-R	5.6
321	Elliot, 1990	58	60	DAS	SB4	0.8
322	Elliot, 1990	55	119	DAS	SB4	1.16
323	Elliot, 1990	29	103	DAS	SB4	1.93
324	Elliot, 2007	95	57.6	DAS-IIff	WPPSI-III	0.72
325	Estabrook, 1984	152	120	WJTCA	WISC-R	1.38
326	Fagan et al., 1969	32	65	WPPSI	SB 60	1.62
327	Gregg & Hoy, 1985	50	268.8	WAIS-R	WJTCA	1.06
328	Harrington et al., 1992	10	36	WPPSI-R	WJTCA-R	−16.4
329	Hayden et al., 1988	32	111.6	SB4	K-ABC	−1.85
330	Hendershott et al., 1990	36	48	SB4	K-ABC	1.81
331	Ingram & Hakari, 1985	33	124.8	WJTCA	WISC-R	0.70
332	Ipsen et al., 1983	27	108	WJTCA	WISC-R	0.68
333	Ipsen et al., 1983	19	108	WJTCA	WISC-R	0.65
334	Ipsen et al., 1983	14	108	WJTCA	WISC-R	0.60
335	Kaufman & Kaufman, 1993	79	204	KAIT	SB4	0.14
336	Kaufman & Kaufman, 2004	86	138	K-ABC-II	WJTCA-IIIgg	−0.09
337	Kaufman & Kaufman, 2004	56	138	K-ABC-II	WISC-IV	−4.6
338	Kaufman & Kaufman, 2004	36	42	K-ABC-II	WPPSI-III	−2.8
339	Kaufman & Kaufman, 2004	39	66	K-ABC-II	WPPSI-III	−7.6
340	Kaufman & Kaufman, 2004	80	136	KBIT-II	WASIhh	0.76
341	Kaufman & Kaufman, 2004	62	512	KBIT-II	WASI	1
342	Kaufman & Kaufman, 2004	63	130	KBIT-II	WISC-IV	−1.3
343	King & Smith, 1972	24	72	WPPSI	SB 60	0.74
344	Knight et al., 1990	30	115	SB4	K-ABC	0.54
345	Krohn & Traxler, 1979	22	39	SB 72	MSCA	−1.2
346	Krohn & Traxler, 1979	24	54	SB 72	MSCA	−5.73
347	Krohn & Lamp, 1989	89	59	SB4	K-ABC	0.61
348	Lamp & Krohn, 2001	89	59	SB4	K-ABC	0.56
349	Lamp & Krohn, 2001	72	81	SB4	K-ABC	1.41
350	Lamp & Krohn, 2001	75	104	SB4	K-ABC	0.28
351	Law & Faison, 1996	30	182.4	KAIT	WISC-III	−17.4
352	Naglieri & Harrison, 1979	15	88	SB 72	MSCA	24.26
353	Oakland et al., 1971	24	74	WPPSI	SB 60	0.7
354	Oakland et al., 1971	24	72	WPPSI	SB 60	0.76
355	Pasewark et al., 1971	72	67.11	WPPSI	SB 60	0.78
356	Phelps et al., 1984	55	188	WJTCA	WISC-R	0.54
357	Prosser & Crawford, 1971	50	58	WPPSI	SB 60	1.5
358	Reeve et al., 1979	51	111	WJTCA	WISC-R	3.04
359	Reilly et al., 1985	26	84	WISC-R	MSCA	2.5
360	Reilly et al., 1985	26	84	WJTCA	WISC-R	−0.65
361	Rellas, 1969	26	76	WPPSI	SB 60	3.40
362	Roid, 2003	145	96	SB5	WJTCA-III	0.46
363	Smith et al., 1989	18	125	SB4	K-ABC	0.48
364	Thompson & Brassard, 1984	20	122.4	WJTCA	WISC-R	0.25
365	Thompson & Brassard, 1984	20	120	WJTCA	WISC-R	2.21
366	Thompson & Brassard, 1984	20	120	WJTCA	WISC-R	2.47
367	Thorndike et al., 1986	175	84	SB4	K-ABC	−0.09
368	Thorndike et al., 1986	30	107	SB4	K-ABC	0.4
369	Vo et al., 1999	30	147	KAIT	WISC-III	−1.34
370	Vo et al., 1999	30	175	KAIT	WISC-III	−4.28
371	Wechsler, 1967	98	66.5	WPPSI	SB 60	0.34
372	Wechsler, 1991	27	108	WISC-III	DAS	−2.8
373	Wechsler, 1999	248	623.76	WASI	WAIS-III	−0.14
374	Ysseldyke et al., 1981	50	123	WJTCA	WISC-R	1.80
375	Zimmerman & Woo-Sam, 1970	26	72	WPPSI	SB 60	1
376	Zimmerman & Woo-Sam, 1970	21	72	WPPSI	SB 60	2.54
377	Zimmerman & Woo-Sam, 1974	22	72	WPPSI	SB 60	1.2
378	Zimmerman & Woo-Sam, 1974	22	66	WPPSI	SB 60	2.54

^aAge reported in months.

^bModern comparisons with at least five years between test norming periods.

^cStanford-Binet Intelligence Scales – Fourth Edition.

^dStanford-Binet Intelligence Scales – Form L-M (1972 norms ed.).

^eWechsler Intelligence Scale for Children-Revised.

^fWechsler Adult Intelligence Scale-Revised.

^gWechsler Intelligence Scale for Children – Third Edition.

^hWechsler Intelligence Scale for Children – Fourth Edition.

ⁱWechsler Adult Intelligence Scale – Third Edition.

^jWechsler Preschool and Primary Scale of Intelligence-Revised.

^kStanford-Binet Intelligence Scales – Fifth Edition.

^lStanford-Binet Intelligence Scales – Form L-M.

^mWechsler Preschool and Primary Scale of Intelligence – Third Edition.

ⁿWechsler Adult Intelligence Scale – Fourth Edition.

^oAll other comparisons with at least five years between test norming periods.

^pWechsler Intelligence Scale for Children.

^qMcCarthy Scales of Children’s Abilities.

^rWechsler Preschool and Primary Scale of Intelligence.

^sStanford-Binet Intelligence Scales – Form L.

^tKaufman Brief Intelligence Test.

^uWechsler Adult Intelligence Scale.

^vDifferential Ability Scales.

^wStanford-Binet Intelligence Scales – Form L-M (1960).

^xKaufman Assessment Battery for Children.

^yWoodcock-Johnson Tests of Cognitive Abilities.

^zKaufman Brief Intelligence Test – Second Edition.

^aaKaufman Assessment Battery for Children – Second Edition.

^bbKaufman Adolescent and Adult Intelligence Test.

^ccModern comparisons with less than five years between test norming periods.

^ddAll other comparisons with less than five years between test norming periods.

^eeWoodcock-Johnson Tests of Cognitive Abilities-Revised.

^ffDifferential Ability Scales – Second Edition.

^ggWoodcock-Johnson Tests of Cognitive Abilities – Third Edition.

^hhWechsler Abbreviated Scale of Intelligence.

Overall Model

The mean effect over 285 total studies (n = 14,031) in the random effects model was 0.231 IQ points per year, 95% CI [0.20, 0.26], z = 14.10, p < .0001, with a confidence interval and p-value indicating that the Flynn effect is different from zero¹. The effects were significantly heterogeneous, (Q₍₂₈₄₎ = 4710, p < .0001). The estimated I², or proportion of the total variance due to true study variance, was I² = 0.94. The Tau, or estimated standard deviation of the true effects, was τ = 0.25, resulting in a credibility interval of −0.26 to +0.72. Eighty-two percent of the distribution of true effects was above zero.

Distribution of Effects

The effects were plotted against their standard error in a funnel plot (Figure 1). There is no apparent publication bias, which would be represented by a gap on the lower left side of the plot. A similar absence of a gap is seen on the lower right side of the plot. What is most apparent in the funnel plot is that many effects fall outside the 1.96 standard error line, suggesting that there is important true heterogeneity in these effects that is not consistent with sampling error alone.

Figure 1.

Study effect sizes and standard errors included in the overall model.

Moderator Analysis

We first modeled the significant heterogeneity in the effect sizes as a function of test set. There was a significant between-test group effect, Q₍₅₎ = 231, p < .0001, with test group explaining 5.2% of the explainable variance in effects. We then regressed all effects on ability level using Unrestricted Maximum Likelihood for mixed meta-regression within Comprehensive Meta-Analysis software (Borenstein et al., 2005). The range of ability means in the set of effects was 40.6–132.7 standard score points. The intercept was significant (a = 0.38, z = 2.58, p < .01), but the slope was not (b = −.002, z = −1.08, p < .28), indicating that the effect did not change significantly over the range of ability levels represented in this set of effects.

Further Analysis within Test Groups

We completed separate meta-analyses within test groups to place the results of the modern tests within the context of this larger set. This was done so we could meaningfully compare our results to Flynn’s (1984a, 2009a) and Flynn and Weiss’ (2007) results, which were based on data published after 1972. Because our focus is on the modern set, we conducted moderator analyses only within that set.

Older Wechsler/Binet tests

The mean effect (k = 152, n = 5,550) of studies involving Wechsler/Binet scales normed before 1972 (and including other IQ tests with an older normative basis) in the random effects model was 0.23 IQ points per year, 95% CI [0.19, 0.27], z =11.12, p < .0001. The effects were significantly heterogeneous, (Q₍₁₅₁₎ = 3237, p < .0001). The estimated I², or proportion of the total variance due to true study variance, was I² = .95, indicating that very little of the variance in observed effects was attributable to sampling error or unreliability in the tests. The Tau, or estimated standard deviation of the true effects, was τ = 0.24, indicating a 95% credibility interval of −0.23 to +0.70. In other words, approximately 84% of the distribution of true effects was above zero.

Screening tests

The mean effect (k = 17, n = 1,325) in the random effects model was 0.02 IQ points per year, 95% CI [−0.15, 0.19], z = 0.21, p < .84. Although the mean effect was not significantly different from 0, the effects were significantly heterogeneous (Q₍₁₆₎ = 232, p < .0001). The estimated I², or proportion of the total variance due to true study variance, was I² = .93. The Tau, or estimated standard deviation of the true effects, was τ = 0.33, indicating a 95% credibility interval of −0.63 to +0.66, indicating that more than half of the true effects were above zero.

KABC tests

The mean effect (k = 34, n = 1,611) in the random effects model was 0.02 IQ points per year, 95% CI [−0.16, 0.19], z = 0.19, p = .85. Although the mean effect was not significantly different from zero, the effects were significantly heterogeneous (Q₍₃₃₎ = 295, p < .0001). The estimated I², or proportion of the total variance due to true study variance, was I² = .89. The Tau, or estimated standard deviation of the true effects, was τ = 0.47, indicating a 95% credibility interval of −0.90 to +0.93. Again, more than half of the true effects were positive.

Other modern tests

The mean effect (k = 12, n = 925) for the modern tests other than Wechsler and Binet pairs normed since 1972 in the random effects model was 0.30 IQ points per year, 95% CI [0.21, 0.40], z = 6.13, p < .0001. Although the mean effect was significantly different from zero, the effects were significantly heterogeneous (Q₍₁₁₎ = 44, p < .0001). The estimated I², or proportion of the total variance due to true study variance, was I² = .75. The Tau, or estimated standard deviation of the true effects, was τ = 0.14, indicating a credibility interval of 0.03 to +0.57. For the other modern effects, 98.6% of the true effects were positive.

McCarthy test comparisons

The mean effect (k = 14, n = 557) in the random effects model involving the McCarthy was 0.33 IQ points per year, 95% CI [0.15, 0.51], z = 3.60, p < .0001. Although the mean effect was significantly different from zero, the effects were significantly heterogeneous (Q₍₁₃₎ = 74, p < .0001). The estimated I², or proportion of the total variance due to true study variance, was I² = .83. The Tau, or estimated standard deviation of the true effects, was τ = 0.28, indicating a credibility interval of −0.23 to +0.89. For this set of tests, 87.8% of the true effects were positive.

Modern Wechsler/Binet tests

The mean effect (k =56, n = 4,063) for the Wechsler and Binet tests normed since 1972 in the random effects model was 0.35 IQ points per year, 95% CI [0.28, 0.42], z = 10.06, p < .00001. Although the mean effect was significantly different from zero, the effects were significantly heterogeneous (Q₍₅₅₎ = 597.34, p < .0001). The estimated I², or proportion of the total variance due to true study variance, was I² = .91. The Tau, or estimated standard deviation of the true effects, was τ = 0.23, indicating a credibility interval of −0.10 to +0.80. For the modern effects, 93.5% of the true effects were positive.

Moderator Analyses of the Modern Tests

Ability level

The first moderator selected to explore the significant heterogeneity of the modern tests was ability level. The significant mixed effects meta-regression slope of effect size on ability level was b = −.01, 95% CI [−.016, −.004), z = −3.37, p < .0007. The Q for the model in this analysis was 11.38, accounting for 15.8% of the total variability as estimated by the Unrestricted Likelihood method.

Inspection of Figure 2 revealed an unusual bimodal pattern in the effects representing samples with the lowest ability. This pattern indicates that some of the lower ability samples had higher than average Flynn effects whereas others had lower than average Flynn effects. In order to understand this pattern and its apparent contribution to the heterogeneity of the set of effects, we looked carefully at each of the ten lowest ability studies. Of the five studies with the highest effect sizes in this group (Gordon, Duff, Davidson, & Whitaker, 2010; Nelson & Dacey, 1999; Spruill, 1991; Thorndike, Hagen, & Sattler, 1986), four were comparisons between Stanford-Binet-4 (SB-4) and Wechsler Adult Intelligence Scales-Revised (WAIS-R). The lowest possible score on the SB-4 is 36, and the lowest possible score on the WAIS-R is 45. Individuals who obtain the lowest possible score on both tests will still have an apparent difference in their standard scores of 9 points. Consistent with the plot, as the scores get closer to the mean of 100, the differences in the scales become smaller, and the effects become smaller.

Figure 2.

Study effect size regressed on sample ability in the modern set.

A different factor was noted in the three unusually low effects at the low ability side of the plot. For two of these effects, the administration of the tests was not counterbalanced. All subjects received the old test first. It is possible that for these comparisons, the participants performed better on the second (newer) test than on the first due to an order effect (see below). Effects for the two non-counterbalanced studies fall below the regression line and are the second and fourth from the lowest in ability in that cluster. One (Thorndike, Hagen, & Sattler, 1986) was a comparison of SB4 with Stanford-Binet L-M (floor = 36 points on both tests) and the other (Thorndike, Hagen, & Sattler, 1986) was a comparison of SB-4 with the Wechsler Intelligence Scales for Children-Revised (WISC-R). To evaluate the influence of these potentially highly influential but atypical effects to the analysis, we ran a cumulative analysis of the meta-analytic effect. We arranged all modern effects in descending order by ability level and then added them to the meta-analysis one at a time.

Figure 3 depicts a cumulative chart of all of the effects produced from the modern set, with scores ordered from left to right with ability on the horizontal axis and average effect size on the vertical axis. After including the one study with the highest level of ability, the effect was approximately −0.05. With the addition of the second study, the average effect was about 0.45. By the time approximately 20 studies had been included, the effect stabilized and once all but the lowest ability 10 studies were included, the estimate was 0.28. The addition of the last effects did indeed have a large impact, bringing the overall mean back up to 0.35. Eliminating the three lowest ability effects results in a mean estimate of the remaining 53 effects (n = 3,951) of 0.293 points per year, 95% CI [0.23, 0.35], and the regression of effect on ability is no longer significant. The other five studies that are part of the bimodal distribution in Figure 2 do not appear to have significant impact on the overall estimate.

Figure 3.

Cumulative Flynn effect by decreasing sample ability.

Age

Effect size was regressed on the average age of each sample in the set of 53 effects (n = 3,951) retained in the ability analysis above. The regression of effect size on age was nonsignificant, accounting for less than one percent of the variance in effect sizes.

Sample type

Each modern study (k=53) was coded for sample type, which included clinical (k = 1, n = 24), research (k = 22, n = 902) and manuals (k = 30 n = 3,025). Because there was only 1 effect from a clinical sample, the moderator analysis was done on the remaining 52 effects. Although each group mean effect was significantly different from zero (Table 2), type of sample was not significant in the random effects analysis, Q₍₁₎ = 3.14, p < .076.

Table 2.

Flynn Effect by Sample Type

Sample	N	Mean	SE	Lower CI	Upper CI	z	p<
Clinical	1	0.36	0.11	0.15	0.57	3.34	0.001
Research	22	0.39	0.08	0.23	0.55	4.76	0.0001
Manuals	30	0.23	0.03	0.17	0.30	7.11	0.0001

Order effects

Table 3a summarizes estimated Flynn effects (random effects model) by test group for studies that were counterbalanced. The pattern of effect sizes paralleled the overall study results for each test group. For the modern tests, summarized in Table 3b, the estimate of 0.28 is close to the estimate of 0.29 for all 53 effects. Within the 53 modern effects, 50 provided information on test order. Most studies either uniformly gave the tests in the same order or counterbalanced so that half got the old test first and half got the new test first. The order effect was not significant in the random effects analysis, Q₍₂₎ = 4.30 p < .17. The mean effects for the counterbalanced group (k = 30, n = 2,912) (M = 0.29, 95% CI [0.23, 0.36]) and the group of effects where the old test was given second (k = 8, n = 505) (M = 0.54, 95% CI [0.16, 0.91]) were significantly different from zero. The mean effect for the studies where the older test was given first (k = 12, n = 396) was not significantly different from zero (M = 0.14, 95% CI [−.04, 0.32]).

Table 3.

a
Flynn Effect by Test Group for Counterbalanced Administration Only
Group	N	Point estimate	SE	Lower limit	Upper limit
Modern SB/Wa	30	0.29	0.03	0.23	0.36
Modern Otherb	7	0.33	0.08	0.17	0.49
Old SB/Wc	81	0.26	0.03	0.21	0.31
K-ABCd	20	−0.08	0.14	−0.36	0.20
Screeninge	6	0.09	0.06	−0.02	0.20
McCarthyf	12	0.36	0.11	0.15	0.56

b
Flynn Effect by Test Group for Modern Tests with Known Administration Order
Group	N	Point estimate	SE	Lower limit	Upper limit
Flynn effect plus practice effect	8	0.54	0.19	0.16	0.91
Flynn effect less practice effect	12	0.14	0.09	−0.04	0.32
Counterbalanced order	30	0.29	0.03	0.23	0.36

Note. Atypical modern effects have been deleted from these analyses.

^aModern SB/W effects include only Stanford-Binet and Wechsler tests normed in 1972 or later.

^bModern Other includes other tests normed in 1972 or later.

^cOld SB/W includes comparisons of Stanford-Binet and Wechsler tests only, where at least one test was normed before 1972.

^dK-ABC includes comparisons with the K-ABC test.

^eScreening includes effects on screening instruments.

^fRemainder includes effects that do not fall into any of the other categories.

For the effects coded 100 where the old test was uniformly given first, negative effects due to prior exposure would be expected. In this ordering, Table 3b shows that prior exposure reduces the Flynn effect (.14 per year, n.s.). For effects coded 0, we would expect the mean effect to be amplified, reflecting a Flynn effect plus a prior exposure effect. Table 3b shows that the Flynn effect estimate is indeed larger (.54 per year). Finally, if the order was counterbalanced, the estimate should reflect the Flynn effect with less bias than either of the other two estimates. The estimate for the 30 counterbalanced groups is .29 per year. Although the order effect was not statistically significant, the estimates are different from 0 and the order test may not have been adequately powered. The patterns are consistent with hypothesis by Kaufman (2010).

Effect of pairing

Examining the counterbalanced tests permitted a comparison controlling for order effects when pairing Binet/Binet tests (k = 8, n = 545), Wechsler/Wechsler tests (k = 18, n = 2,023), and Wechsler/Binet tests (k = 4, n = 344). These comparisons yielded similar estimates close to the overall estimate of 0.293 per year: Binet/Binet: M = .291, 95% CI [0.14, 0.45]; Wechsler/Wechsler: M = 0.296, 95% CI [0.22, 0.38]; Wechsler/Binet: M = 0.292, 95% CI [0.17, 0.42].

Sensitivity Analysis

Finally, we explored the effect of our decisions on the results of the meta-analysis. First, the formula for the variance of each study included the sample-specific correlation between the two tests being compared in a given study. This correlation, however, is subject to sampling variance and to possible restriction of range within the sample studied. It is also potentially attenuated below the population correlation between the two tests if the administration is done in such a way as to affect the actual reliability of the tests as given. For example, test directions might be misunderstood or misread, the testing environment might introduce distractions, or there might be inaccuracies in scoring. As an alternative, we calculated the average r for each pair of tests by converting all observed correlations to Fisher’s z and averaging within test pairs, or by using the overall r, as above, if the specific study was missing the correlation and there were no other studies with the same test pair. For the overall analyses and within the test groups, mean effects differed by no more than 0.03 points per year. All significance tests and tests of heterogeneity resulted in the same conclusions reached above.

In addition to the 285 effects analyzed above, there were an additional 93 effects with norming gaps of 5 years or less. The mean effect over the combined 378 studies in the random effects model was 0.28 IQ points per year, 95% CI [0.25, 0.31], z = 16.83, p < .0001. The effects were significantly heterogeneous, (Q₍₃₇₇₎ = 5581, p < .0001). The estimated I², or proportion of the total variance due to true study variance, was I² = .93, so very little of the variance in observed effects was attributable to sampling error or unreliability in the tests. The Tau, or estimated standard deviation of the true effects, was τ = 0.26, indicating a 95% credibility interval of −0.23 to +0.79. In other words, approximately 86% of the distribution of true effects was above zero. The funnel plot for the entire set of effects can be seen in Figure 4. Note that the 285 effects captured in Figure 1 comprise the tip of this pyramid. The range of standard errors in Figure 1 is from 0.0 to +0.6, whereas in Figure 4, the range is 0.0 to +20.0.

Figure 4.

Complete set of study effect sizes and their standard errors.

Discussion

Major Findings

The overall Flynn effect of 2.31 produced by this meta-analysis was lower than Flynn’s (2009a) value of 3.11 and Fletcher et al.’s (2010) value of 2.80. It also fell below Dickinson and Hiscock’s (2010) estimate of 2.60, which was the average of separate calculations for each of the 11 Wechsler subtests. However, our overall comparisons included all identified studies back to 1951. When a meta-analytic mean was calculated for the modern set (composed exclusively of 53 comparisons involving the Wechsler/Binet and excluding 3 atypical comparisons, and more comparable to the studies from Flynn [2009]), the Flynn effect was 2.93 points per decade, a value larger than estimates based on studies that included older data. This value is the most reasonable estimate of the Flynn effect for Wechsler/Binet tests normed since 1972 and is similar to the 3 points per decade rule of thumb commonly recommended in practice. The standard error of this estimate is less than 1 point (SE = 0.35).

Moderator Analyses

Ability level

Defined as the score produced by the most recently normed IQ test, ability level did not explain a significant amount of variance in the Flynn effect in the overall model. Although the literature has produced inconsistent evidence with regard to the direction and/or linearity of the relation between ability level and mean Flynn effect (Zhou et al., 2010; Lynn & Hampson, 1986; Teasdale & Owen, 1989; Graf & Hinton, 1994; Sanborn et al., 2003; Spitz, 1989), the present data revealed no relation between these two variables in the overall analysis. This finding may be the result of a methodological difference between our meta-analysis, which treated ability level as a continuous variable, and previous studies, many of which treated ability level as a categorical variable.

Within the set of modern tests, ability level did explain a significant amount of variance in the Flynn effect, with lower ability samples producing higher Flynn effects. However, this was not a clearly reliable finding. The distribution of effects at lower ability levels was bimodal, with a subsample of comparisons producing higher than anticipated Flynn effects and another subsample of comparisons producing lower than anticipated Flynn effects. When the three effects with the lowest level of ability were deleted, ability was no longer a significant predictor of effect size. Thus, estimating the magnitude of the Flynn effect in lower ability individuals, for whom testing may have the greatest ramifications, appears to be more complex than estimating the magnitude of the Flynn effect in the remainder of the ability distribution. As noted previously, the distribution of Flynn effects that we observed at lower ability levels might be the result of artifacts found in studies of groups within this range of ability. When studies were added one at a time, we obtained stability at about 0.27–0.30 points per year, with a mean of 0.293 points per year (excluding the three atypical low ability studies). These findings suggest that the mean magnitude of the Flynn effect may not change significantly with level of ability and that the correction can be applied to scores across the spectrum of ability level.

Age

Results revealed no difference in the Flynn effect based on participant age, suggesting that the Flynn effect is consistent across age cohorts. This finding is consistent with previous research (Flynn, 1984, 1987).

Sample type

Although the sample type effect was not statistically significant, it was based on a small number of effects and the means were different from zero, with the patterns showing lower Flynn effect estimates for test manual than research studies. We might expect for standardization samples to exercise the most control over variables related to participant selection, testing environment, and test administration procedures, so that the Flynn effect increases as control over these variables is relaxed. Because the sample size constituting the clinical set is so small (k = 1, n = 24), future research with a larger set of studies is needed.

Order of test administration

Test order was not a statistically significant moderator. However, the number of effects per comparison was small and the patterns were consistent with hypotheses by Kaufman (2010). For all test sets that were counterbalanced, the Flynn effect estimates were similar in magnitude and pattern across test sets to the overall estimates. In the modern set, where order varied, the effect for counterbalanced administrations only (M = 0.293, k = 30, n = 2,912) was the same as the overall estimate for the full set of modern tests (M = 0.293, k = 53, n = 3,951, excluding the three atypical low ability studies), reflecting the fact that the bulk of the effects (k = 30) were derived from counterbalanced studies. However, if the new test was given first, the estimate (0.54) was larger, reflecting the additive effects of prior exposure and norms obsolescence. If the old test was given first, the estimate (0.14) was smaller, reflecting the opposing influences of prior exposure and norms obsolescence. Our data do not address Kaufman’s (2010) more specific concern about asymmetric order effects such that taking the newer test first increased subsequent performance on the older test more than taking the older test first increases subsequent performance on the newer test. This putative pattern might be expected when the content or administration of an IQ test or subtest (e.g., Similarities subtest of the WISC-R) is changed in ways that could benefit a child who subsequently encounters the previous version of the same subtest. Given the variety of subtests underlying the IQ scores included in our meta-analyses, and the convergence of Flynn effect estimates around 0.29 for the modern tests, the order effect tends to be transitive with a mean magnitude of approximately ± .20. When the newer test is administered first, the Flynn effect estimate is approximately 0.29 + .20 and, when the older test is administered first, the Flynn effect estimate is approximately 0.35 – .20.

Pairing

Examining just the modern tests administered in a counterbalanced order and excluding the three atypical studies showed that the estimates for pairings of Wechsler/Wechsler, Binet/Binet, and Wechsler/Binet tests (all about 0.29) were remarkably similar to the overall estimate of 0.293 per year. These results suggest that similar corrections can be made to different versions of the Wechsler and Binet tests normed since 1972.

Implications of the Flynn Effect for Theory and Practice

Theory

Genetic hypotheses

As discussed above, there are multiple hypotheses about the basis of the Flynn effect, including genetic and environmental factors, and measurement issues. Although genetic hypotheses have not gained much tractability, they make predictions about relations with age and cohort that can be compared to these results. The larger Flynn estimate in our study for newer than older tests provides no compelling support for the heterosis hypothesis.

Environmental factors

Our finding that the Flynn effect has not diminished over time and may be larger for modern than older tests is not consistent with Sundet et al.’s (2008) hypothesis relating increasing IQ scores and decreasing family size, although we do not have data for a direct evaluation.

The larger effect for modern than older tests could be regarded as consistent with Lynn’s (2009) hypothesis pertaining to pre- and early postnatal nutrition. However, although we cannot directly address cohort effects in this meta-analysis, we note that the magnitude of increases in Wechsler and SB scores has remained close to the nominal value of 3 IQ points per decade since 1984 (Flynn, 2009). Deviations from this constant value--such as the difference we found between modern and old tests--might indicate an IQ difference between older and younger cohorts, but it also might reflect other differences that have occurred over time, such as scaling changes, ceiling effects, or differences in the sampling of study participants (e.g., Kaufman, 2010; Hiscock, 2007).

Our study did not find evidence for the plateauing or decline of the Flynn effect in the United States, as has been documented in Norway (Sundet et al., 2004) and Denmark (Teasdale & Owen, 2008; Teasdale & Owen, 2005), respectively. Table 5.6 in the WAIS-IV manual (Wechsler, 2008) summarizes an excellent planned comparison of the WAIS-III (standardized in 1995) and the WAIS-IV (standardized in 2005) scores administered in counterbalanced order to 240 examinees. This table shows results similar to our meta-analysis, with average WAIS-III scores about 3 points higher than WAIS-IV scores. In addition, the effect was similar across age and ability level cohorts. To the extent that the United States and Scandinavia differ on at least the variables proposed to be related to the plateauing of scores in Scandinavia (e.g., family life factors [Sundet et al., 2004] and educational priorities [Teasdale & Owen, 2008; Teasdale & Owen, 2005]), we might anticipate the difference in IQ score patterns noted. For example, Scandinavia’s parental leave and subsidized childcare might be indices of optimal socioenvironmental conditions and are generous relative to the United States. With regard to educational priorities, the relative value of a liberal arts education persists in the United States.

Measurement issues

Different types of tests yield different estimates of the Flynn effect. The effects were most apparent for multifactorial tests like the Wechsler and Binet scales, and extend to other modern tests with the exception of the KABC, which yielded little evidence of a Flynn effect. This is surprising because the KABC minimizes the need for verbal responses, and Flynn effects tend to be relatively large for nonverbal tests such as the Wechsler Digit Symbol subtest (Dickinson & Hiscock, 2010). In addition, the variability of estimates for the KABC was very high, 95% CI [−0.16, +0.19], 95% credibility interval [−.90, +.93]. Mean estimates were negligible for screening tests, which is surprising because most screening tests include matrix problem-solving tests, which historically have yielded large estimates for norms obsolescence. Again, the variability is high, 95% CI [−0.15, +0.19], 95% credibility interval [−.63, +.66]). Altogether, these results suggest caution in estimating the degree of norms obsolescence for the KABC and different screening tests.

Practice

Assessment and decision-making

The results of this meta-analysis support the persistent findings of a significant and continuous elevation of IQ test norms as described by Flynn (1984, 1987, 1998, 1999, 2007). The rate of change obtained from the overall model was somewhat less pronounced than the 3 IQ points per decade typically cited. Nevertheless, when only the modern Wechsler/Binet tests were considered in isolation, the magnitude of the effect appears to be close to 3 points per decade and showed no evidence of reducing in magnitude. Our support for a robust Flynn effect, manifested across various tests in nearly 300 studies, underscores the importance of considering this factor in high stakes decisions where the cut point on an IQ test is a salient criterion. These decisions include assessments for intellectual disability, which have implications for educational services received in schools, the death penalty, and financial assistance in cases where the individual is not competent to work.

Intellectual disability professionals have debated the necessity of correcting IQ scores for the Flynn effect in decisions about intellectual disability (e.g., Greenspan, 2006; Moore, 2006; Young, Boccaccini, Conroy, & Lawson, 2007). The present findings, which demonstrate the pervasiveness and stability of the Flynn effect across multiple tests and many decades, support the feasibility of correcting IQ according to the interval between norming and administration of the test, i.e., according to the degree to which the norms have become obsolete (Flynn, 2006a, 2009a). A precise correction, however, cannot be assured in all circumstances because the Flynn effect, as it applies to a given test, may strengthen or weaken at any time in the future. Moreover, the exact size of the Flynn effect may vary from one sample to another. Nonetheless, the rough approximation of 3 points per decade (plus or minus about 1 point based on the standard error and a 95% confidence interval) is consistent with the results of the modern studies in this meta-analysis.

Correction for the Flynn effect, although it increases the validity of the measured IQ (Flynn, 2006a, 2007, 2009a), does not justify using a conventional cut point as the sole criterion for determining intellectual disability (cf. Flynn & Widaman, 2008). In other words, increasing the validity of the measured IQ does not diminish the importance of other factors, including adaptive behavior. These include skills related to interpersonal effectiveness, activities of daily living, and the understanding of concepts such as money (AAIDD, 2010). Research has demonstrated a positive relation between IQ and measures of adaptive behavior (Schatz & Hamdan-Allen, 1995; Bolte & Poustka, 2002), and this supports the potential importance of considering both kinds of information when high stakes decisions must be made (Flynn & Widaman, 2008).

The results of this meta-analysis suggest that examiners be mindful about the particular tests administered in situations where an individual is retested to assess for progress and to determine the necessity of special education services. The significant Flynn effect means that, when individuals are tested near the release of a newly normed assessment, the difference in IQ scores produced by the newer test and the older test would indicate that the individual is performing more poorly than what earlier testing may have suggested. A critical implication was highlighted in a recent article by Kanaya and Ceci (2012), who observed that children administered the WISC-R during a special education assessment and administered the WISC-III during a reevaluation were less likely to be rediagnosed with a learning disorder than children administered the WISC-R on both occasions. Unawareness of the Flynn effect on the part of test examiners can compound this problem. For example, Gregory and Gregory (1994) raised concerns that at the time of its publication, the Revised Neale Analysis of Reading Ability was producing lower scores than the older British Ability Scales (BAS) Word Reading scale. A critique of Gregory and Gregory’s (1994) concerns by Halliwell and Feltham (1994) and possible explanations for the findings ensued, yet no mention of the possibility of norms obsolescence was presented. Our data show that norms obsolescence could have significant ramifications for the test results of students.

Further, in cases where an individual is assessed at two different sites (e.g., when a child moves and is assessed in a different school district), it may be possible for the child to have completed the newer version of a test first, especially if the assessments are occurring near to the release of a newly normed assessment. In this case, the IQ score produced by the second assessment may be particularly inflated due to both the Flynn effect and prior exposure. This child may be more likely to receive a diagnosis of a learning disability during this second assessment than a recommendation of special education services. This example underscores the importance of correcting for the Flynn effect in high stakes decisions, a directive consistent with AAIDD’s (2010) recommendation, but addressed in few state special education standards for determining intellectual disability

Future research

The need for better estimates of the Flynn effect in research pertains to attempts to assess the breadth of the Flynn effect across cognitive domains. Several recent studies indicate that the Flynn effect is not limited to intelligence tests but may be measured in tests of memory (Baxendale, 2010; Rönnlund & Nilsson, 2008, 2009) and object naming (Connor, Spiro, Obler, & Martin, 2004), as well as certain commonly used neuropsychological tests (Dickinson & Hiscock, 2011). As Flynn effect estimates become more precise, it should be possible to differentiate not only the presence or absence of the effect but also gradations in the strength of the effect. Being able to quantify the magnitude of the Flynn effect in various domains would constitute an important advance toward answering the ultimate Flynn effect question, i.e., the underlying mechanism of the phenomenon.

From differences in the rates at which scores from the various Wechsler subtests have risen over time, Flynn (2007) has inferred characteristics of the intellectual skills that are rising rapidly and of the skills that are relatively static. We did not address this issue in this metaanalysis, partly because of the focus on the impact and precision of Flynn effect estimates for high stakes decisions across a range of tests and because the greater impact of the Flynn effect on fluid versus crystallized intelligence is well-established. More relevant would be additional knowledge about the strength of the Flynn effect on tests of memory and language and various neuropsychological tests, which would facilitate a more complete characterization of other higher mental functions that are susceptible to the Flynn effect in varying degrees. The data available from tests other than IQ tests are not likely to be sufficient in quality or quantity to yield precise Flynn effect estimates, but precise estimates for IQ tests will provide a reliable standard against which data from other tests can be evaluated.

Limitations

The objective of the current study was to build upon Flynn’s (2009a) foundational work and Fletcher et al.’s (2010) meta-analytic study on the rate of IQ gain among modern Wechsler-Binet tests per test manual validation studies by expanding the scope of investigation to other tests, eras, and samples. As such, the approach to the current study replicates the method of Flynn (2009a) and Fletcher et al. (2010) by examining intragroup change in IQ score as a function of the norming date of the test. An alternate approach, taken by Flynn (1987) and others since (e.g., Sundet et al., 2004; Sundet et al., 2008) broadens the perspective from intragroup to intergroup change by focusing on draft board test performance within countries in the practice of administering IQ tests to all young men being assessed for suitability for conscription. For the study of a cohort phenomenon like the Flynn effect, this approach is appropriate. Unfortunately, no comparable data exist for American young men. Whereas the Raven’s test administered to Scandinavian young men has not changed in format or content since its development, this is not the case for the Armed Services Vocational Aptitude Battery (arguably a measure of literacy rather than intelligence per se [Marks, 2010]) administered to potential conscripts in the United States. In addition, the data collected from Scandinavian young men, most of whom are evaluated for suitability for the armed services, are more representative of the Scandinavian population than potential conscripts in the United States who self-select into the armed services are of the American population.

There are drawbacks to studying the Flynn effect on the basis of IQ test validation studies per the method of Flynn (2009a) and Fletcher et al. (2010): sample sizes tend to be small; the earlier and later versions of the same test may differ significantly in format or content (e.g., Kaufman, 2010); there may be significant order effects; many tests are never re-normed and therefore lie beyond the reach of this method; and direct within-examinee comparisons have not been made for many tests even if the tests have been re-normed. In addition, validation studies rely on group-level data and presuppose a representative normative basis for the derivation of a standardized IQ score.

Even in the absence of speculation about the representativeness of a normative sample (see Flynn [2009] and Fletcher et al. [2010] for a discussion of the representativeness of the WAIS-III normative sample), normative sample sizes are significantly reduced once stratified by age. For example, 2,200 children constituted the WISC-IV standardization sample, from which were derived norms for subsets of 11 age groups. Similarly, 4,800 individuals constituted the SB5 standardization sample, from which were derived norms for subsets of 23 age groups.

Our alternative method involves relating mean scores on a test to the interval between norming and testing. This third method is capable of detecting changes in test performance over time without the need to track scores over many years or to restrict our analysis to tests for which repeated- measures data have been collected by test publishers. Our method is not as direct as Flynn’s tracking of raw scores on Raven’s Matrices, nor does it provide the detailed information that can be obtained by comparing old and new versions of the Wechsler and Stanford-Binet batteries in the same individuals. On the other hand, our method has the advantage of being applicable to a very large number of informative samples. Our study not only confirms the findings for the Wechsler and Stanford-Binet tests that were obtained using the second method, but it also expands those findings to include numerous tests on which the Flynn effect could not otherwise be assessed. The results show that the IQ increase is pervasive, not only with respect to geography and time, but also with respect to the tests used to measure IQ. Our findings also suggest that the typical 6 IQ points per decade rise in Raven’s Matrices score is unrepresentative of the Flynn effect magnitude measured with most other tests. Most of the tests included in our meta-analysis show rates of increase that are comparable to those measured for the Wechsler and Stanford-Binet batteries. Additionally, the large number of studies included in our meta-analysis provides a strong empirical basis for concluding that comparable IQ increases are evident in samples ranging from preschool children to elderly adults.

Relying on one numerical value to represent a continuous variable, including IQ score and age, results in a significant loss of information. For example, mean values can be greatly influenced by the number and magnitude of extreme values such that the resulting value may not be an adequate measure of central tendency nor an effective illustration of the relation between IQ score and the moderators assessed. Nonetheless, because the correction for the Flynn effect is not a correction to an individual score, but to the normative basis to which individual scores are compared, concerns about applying group data to individual scores do not really apply (Flynn, 2006a).

The usefulness of a meta-analysis depends to a great extent on the accessibility of studies meeting inclusion criteria. Although a thorough review was conducted on PsycINFO® and in test manuals, possibly there were studies meeting inclusion criteria that were not accessed. However, the number of comparisons included in this review appears more than sufficient to assess the magnitude of the Flynn effect and the precision of the obtained value, and to address the additional research questions under consideration. Further, there was no dearth of effect sizes at the lower end of the distribution of effect sizes (Figure 1), which suggests there was no oversampling of studies producing higher Flynn effects.

The homogeneity analysis indicated that there were sources of substantial heterogeneity among the studies included in the meta-analysis. In fact, 91% of the variance in the Flynn effect was due to true variance among studies. The selected moderator variables explained small amounts of the true variance in the modern set, suggesting that additional factors that explain variance in the Flynn effect have yet to be identified.

Conclusions

For the present, the need to correct IQ test scores for norms obsolescence in high stakes decision-making is abundantly clear. At average levels of IQ, a score difference of 95 and 98 is not critical. However, in capital punishment cases, life and death may reside on a 3-point difference of 76 versus 73, or 71 versus 68. This becomes especially important when comparing IQ test scores across a broad period of time and when IQ test scores obtained in childhood are brought to bear on an adult obtained score. Correcting for norms obsolescence is a form of scaling to the same standard. Weight standards often are adjusted each decade because people get larger over time. For these changes, the critical decision points are changed for obesity. For intellectually disability, we could (in theory) use the same test over time. Thus, if a child were assessed in 2013 with the WISC-R standardized in 1973, we could adjust the mean to 109 (SD = 15) and the cut point for intellectual disability to 79 (3 points). Because the convention in our society is to use a cut point of 70, corrections for norms obsolescence, i.e., the Flynn effect, must be made.

The existence of unknown factors that influence the Flynn effect should not obscure the major findings of this study: the mean value of the Flynn effect within the modern set centered around 3 points per decade, most of the estimated distribution of true effects was larger than zero, and the standard error of this estimate is 0.35 (resulting in a 95% CI that extends about .7, rounded to 1 point, on either side of 3 points per decade). These findings are consistent with previous research and with the argument that it is feasible and advisable to correct IQ scores for the Flynn effect in high stakes decisions.