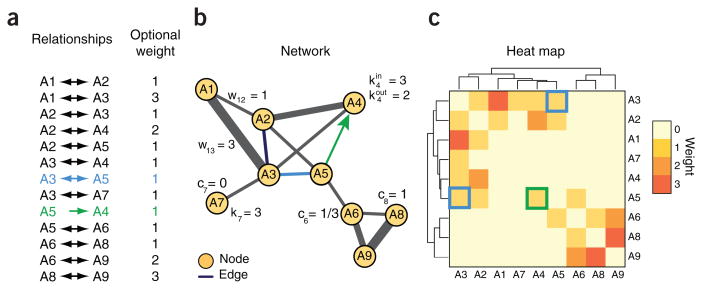
Figure 2.

Mathematical representation of networks and three alternate visualizations of the same data. (a) List of relationships with optional ‘weight’ (often denoted with the letter w), which represent attributes such as relationship significance or stength. Relationships can be undirected (e.g., A3 ↔ A5, shown in blue) or directed (e.g., A5 → A4, shown in green). (b) Network view. Networks are mathematically grounded in the field of graph theory, in which they are commonly denoted G = (V, E), (G, graph; V, a set of vertices or nodes; E, a set of edges). Some commonly encountered mathematical concepts include the node degree (k_i), which is the number of edges attached to a node, and the clustering coefficient (c_i), which counts the number of edges among the neighbors of a node, divided by the maximal possible number of such edges. If edges have directions, it is useful to distinguish between the in-degree (kⁱⁿ_i) and the out-degree (k^out_i). The node degree distribution and average clustering coefficient have been used to characterize different types of networks¹³. (c) Heat map view. Nodes are represented along the sides of the heat map and elements of the map (small squares) are colored according to edge weight, with higher weights having a darker color. Similar rows and columns are placed adjacent to each other, as shown by the similarity tree on each map axis. This view is useful for finding nodes with similar neighbors¹⁴.