Frequency-dependent conspecific attraction to food patches

Abstract

In many ecological situations, resources are difficult to find but become more apparent to nearby searchers after one of their numbers discovers and begins to exploit them. If the discoverer cannot monopolize the resources, then others may benefit from joining the discoverer and sharing their discovery. Existing theories for this type of conspecific attraction have often used very simple rules for how the decision to join a discovered resource patch should be influenced by the number of individuals already exploiting that patch. We use a mechanistic, spatially explicit model to demonstrate that individuals should not necessarily simply join patches more often as the number of individuals exploiting the patch increases, because those patches are likely to be exhausted soon or joining them will intensify future local competition. Furthermore, we show that this decision should be sensitive to the nature of the resource patches, with individuals being more responsive to discoveries in general and more tolerant of larger numbers of existing exploiters on a patch when patches are resource-rich and challenging to locate alone. As such, we argue that this greater focus on underlying joining mechanisms suggests that conspecific attraction is a more sophisticated and flexible tactic than currently appreciated.

1. Introduction

Joining food patches discovered by conspecifics is widespread in the animal world and has been considered a major benefit of sociality in many species, ranging from insects to birds and mammals [1–3]. Individuals that rely on conspecific attraction to locate food patches can supplement their own discoveries by exploiting the resources uncovered by conspecifics searching independently, potentially increasing their mean food intake rate while reducing its variance, both important components of fitness [4].

Various rules for joining patches discovered by others have been considered thus far but, surprisingly, few have been justified theoretically. Influential models of group foraging simply assume that a forager should join any food patches discovered by others [5] without considering that the time needed to join a patch may be better used to search for an unexploited patch, or that already exploited patches may be quite depleted when joining occurs. Models that focus on the size of foraging groups variously assume that joining should be independent of, or increase linearly with, the number of conspecifics at the patch [6–8].

Increased attraction to more crowded patches is thought to be favoured, because crowding will provide information about the location of better food patches and large patches can allow more foragers to forage at the same time. However, it may also be the case that crowded patches can be much depleted for later joiners. Conspecific attraction of this type may share features with quorum-sensing systems as the number of individuals choosing a patch may have a positive, nonlinear effect on recruitment [8]. However, this has not been investigated thoroughly.

Another class of group foraging models considers that foragers split their time between searching alone for food patches and searching for opportunities to join patches discovered by others [9]. Such scrounging inevitably reduces the rate of encounter with food patches at the group level but may be the adaptive consequence of individual selection. In a scrounging mode, a forager is expected to join any food patches discovered by the rest of the group regardless of the number of conspecifics present [10]. Earlier scrounging models assumed that joining was instantaneous, but this assumption was relaxed in more recent models to take into account the inevitable time cost of joining a patch elsewhere in the habitat [7,11].

Whether the various rules described above are optimal from the point of view of maximizing food intake rate has not been explored; this is unfortunate, because many predictions from group foraging models may be dependent on the rules used for joining patches. Here, we use a spatially explicit genetic algorithm approach to evolve the best tactic for conspecific attraction to food patches under a broad range of conditions, varying population density and the density and richness of food patches, which are thought to be key factors in the evolution of conspecific attraction.

2. Material and methods

We examine the propensity to join food patches discovered by others as a function of the number of foragers present at the patch. Each forager's tactic consists of five elements, namely, the probability of joining a patch currently exploited by 1,2,3,4 or 5 or more companions. At the beginning of the first generation, these probabilities are randomly chosen from a uniform distribution independently for each tactic element and for each forager. A number of foragers, ranging from 20 to 200 in different runs of the model, are allocated randomly to one of 900 positions on a 30 × 30 square grid. A fixed number of food patches are randomly located on the grid subject to the constraint that each patch occupies a distinct location. Food patches vary in the number of food items present with an equal mixture of low (half the number of food items of a medium patch), medium or high quality (twice the number of food items of a medium patch).

At each time step, individuals search for food patches by moving to one of the four closest cardinal locations. When reaching the boundaries of the grid, the forager bounces in the opposite direction. If a food patch is located, then the forager extracts 1 food item per time step. If no food patch is located, the forager scans the entire habitat, and if no other patches are currently exploited, the forager moves randomly as before. If one or more food patches are currently exploited, the forager determines the number of foragers present at the closest patch and targets it with the probability set by its tactic. Otherwise, the forager moves randomly as before. If the targeted patch becomes depleted during travel time, the forager restarts the scanning process as before. When a patch is depleted, a new patch is created at a new randomly selected location, keeping the total numbers of patches constant during a generation.

One generation lasts 1500 time steps. The above processes are repeated as necessary with the same number of foragers present initially so as to reach a final population of 200. This allows us to examine the effect of forager density while keeping the size of the population under selection constant. At the end of one generation, the 200 foragers are ranked by their feeding rate (number of food items collected/1500). Foragers in the top half pass their tactic directly to a new crop of foragers [12]. The new foragers needed to complete the population take their tactic from a randomly selected forager from the top half. Each element of the tactic can be mutated with the same fixed probability to a new random value taken from a uniform distribution. Once the new population has been created, a new generation starts following the steps described above.

One run of the model consists of 1500 generations, which is sufficient to obtain stable outcomes. Tactic values are averaged over the last 500 generations. The model is run 15 times using different seeds for the random number generator. The mean is provided for each condition tested across a set of 15 runs. We vary the number of foragers on the grid (forager density), the number of food patches (patch density) and the average number of items per patch (patch richness). Across conditions, the total number of food items on the grid remains the same.

3. Results

Marked deviations from the random expectation, namely, a joining probability of 0.5, occur under all conditions tested (figure 1), indicating strong selection pressure to join patches discovered by others. The probability of joining decreases with the number of foragers at a targeted patch and more strongly so when patches are plentiful but relatively poor. The combination of rich but rare food patches increases joining especially when the number of foragers at the patch is higher. The probability of joining decreases with forager density, but typically only when the number of foragers at the patch is higher.

Figure 1.

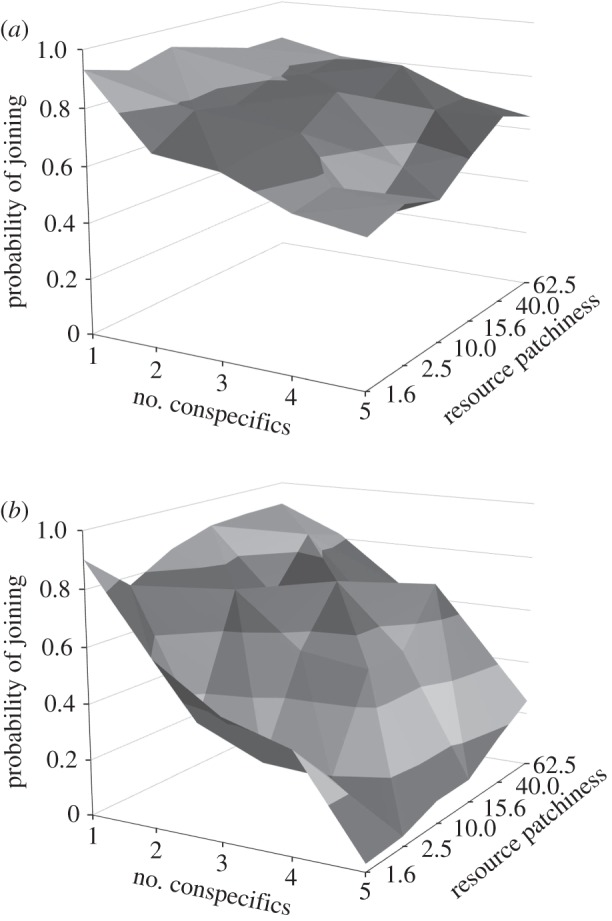
The evolved tactic for joining food patches currently exploited by one to five or more conspecifics as a function of resource patchiness, defined as the number of food items per available patch, in habitats with (a) 20 or (b) 200 foragers. The random expectation for the joining probability is 0.5, the mutation rate 0.0001, and the total number of food items 4000.

4. Discussion

The dynamics of joining food patches discovered by others are complex. The pay-offs from joining depend on the expected amount of resources in a patch at the time of joining, which itself depends on how the population of foragers exploits its resources. The behaviour of foragers is also frequency-dependent as the pay-offs from joining depend on how frequently such choices are made in the population. Our genetic algorithm approach is well-suited to evolve the stable tactic in an environment with frequency-dependent pay-offs and complex feedbacks between foragers and their resources [12].

It is perhaps not surprising that our findings failed to echo the simple assumptions made earlier in group foraging models. In particular, there was no evidence for a positive, nonlinear effect of the number of foragers present at the patch on recruitment, as a quorum-sensing system would predict. Our results emphasize that foragers may be selective in terms of joining less crowded food patches. This might be relevant whenever there is a cost (e.g. in time and/or energy) that must be paid in accessing such foraging opportunities. The costs involve the obvious travel time to these food patches, which may be spent instead on finding patches alone and exploiting such patches without competitors for some time. In addition, the aggregation of foragers that inevitably arises after joining will increase local competition for future food patches [11]. Unless food patches are exceptionally hard to find and quite large, in which case joining any patch represents the only solution, we predict that joining should be negatively frequency-dependent, especially when the population of foragers is large and when food patches are less clumpily distributed. Recent models on the settlement of organisms in patchy habitats, but at a much longer time scale than we have considered here, also stress the importance of the number of conspecifics initially present in a patch [13].

In our model, we have assumed that other foragers sharing the same food patch only have a negative impact on a focal individual through depletion of the patch; however, a range of other mechanisms will apply across different ecological situations. The negative impact may be strengthened if there is interference between individuals sharing a food patch, or if dominant individuals can restrict the food supply to the focal individual [14]. Conversely, the focal individual may benefit from other individuals sharing the food patch if those individuals reduce predation risk and/or enhance the focal individual's access to food [15]. An example of the last situation can occur among scavengers at a large animal carcass, where smaller bodied species can only access the flesh after larger species have sufficiently dismembered the carcass [16].

We have couched our model in terms of food patches, but the range of relevant ecological situations is more general and extends to any situation where one individual can discover a resource but not monopolize access to that resource. The resource could be a receptive female, or an oviposition site, or any food type that is aggregated into units that one individual cannot consume immediately upon discovery.

Although our model makes several testable predictions about conspecific attraction, we stress that empirical testing may be challenging. It is always possible that individuals are attracted to a site not in response to the foragers already present but to some features of the site itself [6]. It may also be difficult to separate instances where a focal individual detected a potential foraging opportunity but rejected the chance to exploit it, as the model predicts, from instances where it failed to detect the foraging opportunity. The first of these challenges can be circumvented by experimental manipulation of the number of competitors on patches [17]. The second issue is more challenging and may require a detailed understanding of the sensory abilities of the species involved. With these caveats in mind, it should be possible to put our predictions to the test to further our understanding of conspecific attraction to aggregated resources in animals.

Data accessibility

The BASIC computer program that we used to generate the data is available using the following link: Dryad (doi:10.5061/dryad.n3m93).