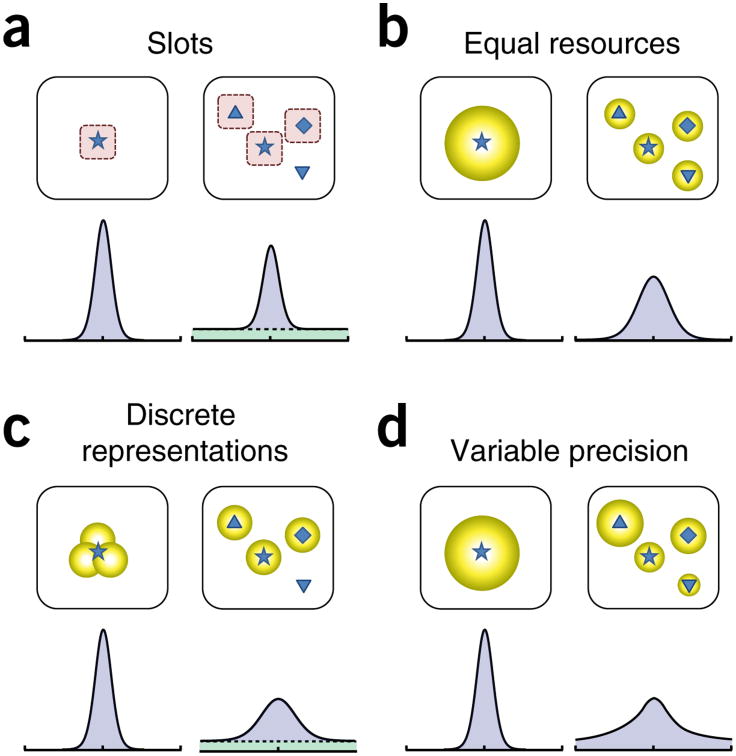
Figure 2.

Models of working memory. (a) In the slot (or item limit) model of working memory^4,5, each visual item is stored in one of a fixed number of independent memory slots (here, 3) with high resolution (left, illustrated, by narrow distribution of errors around the true feature value of a tested item). When there are more items than slots, one or more items are not stored and the slot model predicts that errors in report of a randomly chosen item will be composed of a mixture of high-precision responses (right, blue component of distribution corresponds to trials when the chosen item received a slot) and random guesses (green component corresponds to trials where it did not get a slot). (b) Resource models of working memory^8,11,17 fundamentally differ: they propose a limited supply of representational medium that is shared out between items, without a limit to the number of items that can be stored. Crucially, the precision with which an item can be recalled depends on the quantity of resource allocated to it. If resources are equally distributed between objects, error variability (width of the distribution) increases continuously with the number of items (compare distribution of error for one versus four items), with a normal distribution being commonly assumed. (c) In discrete-representation models¹⁹, the working memory medium is divided into a discrete number of quanta, similar to the slot model. However, these slots are shared out between items; in this respect, this type of model is much closer to resource models than the original slot model (a). For low set sizes (for example, one item shown at left), the quanta combine to produce a high-resolution memory of an item. However, for higher set sizes, above the number of slots available (right), all items get either one or zero quanta, predicting a mixture of low-resolution recall and random guesses. Note how this distribution differs from those in a and b. (d) Variable-precision models^15,16 propose that working memory precision varies, from trial to trial and item to item, around a mean that decreases with increasing number of items as a result of limited resources. This model predicts that recall errors will be made up of an infinite mixture of distributions (assumed normal) of different widths. Variability in precision could stem from variability in resource or from bottom-up factors.