Figure 5.

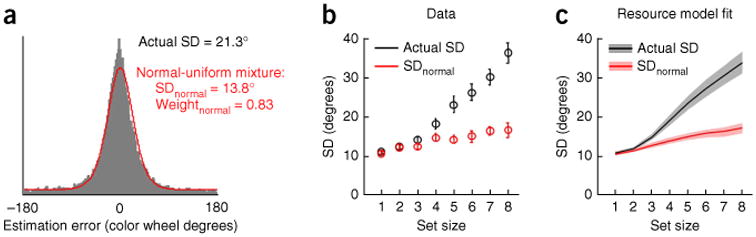
Interpreting the shape and width of working memory error distributions. (a) A crucial area of debate concerns how to model the distribution of recall errors (gray histogram, color estimation data from ref. 15, averaged over all subjects and set sizes). A popular analysis method attempts to do this with a mixture of a circular normal distribution (intended to correspond to items in memory) plus a uniform distribution (intended to correspond to items that are not stored)¹⁹. The red line depicts this fit, also averaged over all subjects and set sizes. Note that the circular standard deviation of the normal component in the mixture, SD_normal (average value given) is much lower than that of the raw data (compare actual standard deviation (actual SD) with SD_normal). The mixture does not fit human recall data well, and the interpretation of the two mixture components has therefore been called into question^15,16. (b) Actual SD and SD_normal as a function of set size. SD_normal substantially underestimates the level of noise in memory, which, if all items are stored, is simply the actual SD. An apparent plateau in SD_normal (red symbols) at higher set sizes has been used to argue for slot models^19,21, but such a plateau is not present in the raw data (black symbols). Data are from ref. 15. Error bars represent s.e.m. (c) A resource model in which all items are stored with variable precision accurately accounts for both actual SD and SD_normal. Thus, SD_normal by itself cannot serve to distinguish between slot and resource models⁶⁹. Adapted from ref. 15; shaded areas are s.e.m. of model fits.