Accurate High-Resolution Measurements of 3-D Tissue Dynamics With Registration-Enhanced Displacement Encoded MRI

Abstract

Displacement fields are important to analyze deformation, which is associated with functional and material tissue properties often used as indicators of health. Magnetic resonance imaging (MRI) techniques like DENSE and image registration methods like Hyperelastic Warping have been used to produce pixel-level deformation fields that are desirable in high-resolution analysis. However, DENSE can be complicated by challenges associated with image phase unwrapping, in particular offset determination. On the other hand, Hyperelastic Warping can be hampered by low local image contrast. The current work proposes a novel approach for measuring tissue displacement with both DENSE and Hyperelastic Warping, incorporating physically accurate displacements obtained by the latter to improve phase characterization in DENSE. The validity of the proposed technique is demonstrated using numerical and physical phantoms, and in vivo small animal cardiac MRI.

I. Introduction

Tissue displacement measurements are useful to obtain kinematic information and deformation metrics, which are associated with functional and material properties often used as indicators of an organ’s state of health. For example, 3-D displacements are useful to characterize skeletal muscle kinematics [1], [2], or to approximate deformation of thin tissues by means of surfaces like in the right ventricle (RV) and blood vessel walls [3], [4]. Localized myocardial strain maps of the left ventricle (LV), often derived from displacement fields, have been shown to be more effective than global parameters like ejection fraction for detecting cardiac abnormalities [5], [6]. Similar approaches have also been used to investigate brain injury [7], [8].

Clinical and experimental characterization of internal tissue motion in vivo has been achieved predominantly by noninvasive medical imaging techniques like ultrasound, computed tomography (CT), and magnetic resonance imaging (MRI) [9]–[11]. Echographic techniques, like speckle tracking, and displacement measurements from Doppler velocity mapping offer the advantages of portability and real-time acquisition, which are often desired for dynamic imaging. However, limited volumetric resolution and issues arising from wave scattering due to density variations around the lungs or bones, make these techniques suboptimal for some applications [12]. Although CT provides high spatial resolution images that can be beneficial and desirable for image registration [13], the modality is yet to be commonly employed for displacement measurements due to its use of ionizing radiation and limited soft tissue contrast.

Because of its soft tissue sensitivity and robust contrast, MRI has become the main tool for the development of several techniques to measure displacement fields [14]. One of the most accepted methods for measuring displacements using MRI consists of creating traceable patterns on the image in a procedure known as tagging [15], [16]. Using the generated grid pattern or its crossings on the magnitude image as fiduciary markers, the technique is still considered by many as the gold standard for 2-D deformation mapping [17], [18]. Automated tag-tracking in 2-D and even in 3-D has been made possible by advances in computer vision and acquisition strategies [1]. The resolution, although traditionally limited to tag spacing, can be improved by interpolation, pattern matching, or harmonic phase analysis (HARP) with extended k-space filters [19], [20].

Other phase-weighted MRI techniques have also been used to measure motion directly without the need for tracking. For example, phase contrast, originally used in MR angiography for velocity mapping [21], [22], has been adapted to approximate tissue motion by integrating a velocity field over time [23]. Alternatively, displacement encoding with stimulated echoes (DENSE) [24]–[26] provides direct displacement weighting. The advantages of DENSE over, for example, tagging include pixel-level resolution, and the ability to encode motion in the through-plane direction as well as in-plane directions. These benefits have fueled the analysis of deformation predominantly in the heart. But practical utility of DENSE has largely been limited by the lack of a generalized approach for relating phase image information to physical displacements, though some recent progress appears promising [27]. The key challenge is to avoid potential problems arising from the angular nature of phase images, like phase wrapping and displacement offsets, which ultimately determine the overall accuracy of the measurements [28], [29].

Besides image acquisition-based methods, displacement can also be obtained by registering anatomical images acquired as the deformation occurs. The approaches include calculating displacements purely from image information with texture correlation [30], [31], local intensity [32]–[36], or other similarity metrics [37], [38]. Registration-based methods are prone to lack of fidelity in areas of poor contrast and numerical ill conditioning. Therefore, image registration continues to be actively studied [39], [40], and has involved using local intensity registration along with fluid [34], or solid [41] deformation schemes to provide regularization and numerical stability. One notable example is Hyperelastic Warping [35], [36], which uses a solid mechanics formulation by means for finite element (FE) modeling. This technique has been shown effective experimentally for deformation characterization of ligaments, blood vessels, and the LV, with different imaging modalities [4], [42], [43]. However, though adding a continuum mechanics model to the registration process can greatly increase its effectiveness, it also introduces dependency on constitutive assumptions and geometric modeling, all of which influence the accuracy of the end result [43].

When investigating tissue displacements noninvasively, it is desirable to obtain accurate information, so that mechanical information from relative deformation metrics and global kinematics of motion can be obtained without the need for a priori assumptions. Likewise, pixel-level resolution is preferred for localizing potential functional deficiencies, or complex motion patterns, even in cases when tissue dynamics involve large deformations over a given amount of time. In response to these requirements, this paper presents a combined method for automatically reconstructing 3-D displacements by using partial image registration information to accurately determine offsets associated with phase unwrapping in DENSE-MRI. The method enables DENSE-MRI to measure highly accurate tissue dynamics between a reference and deformed states without the need for intermediate image acquisition. This report contains the theoretical background underlying the combined analysis, which is followed by verification with numerical images, experimental validation using a moving phantom and a demonstration of the presented concepts in vivo.

II. Theoretical Background

A brief summary of displacement characterization using DENSE-MRI and Hyperelastic Warping is provided to better explain their challenges and remedies. In the ensuing text, vectorial quantities are accented with an arrow, and matrices appear underscored.

A. DENSE-MRI Reconstruction

In DENSE [24]–[26], motion is encoded in the phase angle of the complex MRI signal. Each image contains information about a component of the tissue displacement vector field, $\overrightarrow{u}(\overrightarrow{r})$, in spatial coordinates (deformed configuration), $\overrightarrow{r}$, observed after a deformation has occurred. The motion encoding direction and sensitivity are determined by the combined sensitizing gradients, which are related to the first moment of encoding gradient pulses placed after the first and third RF pulses in the stimulated echo sequence [24]. By expressing the directional encoding sensitivity as a vector ${\overrightarrow{k}}_e$ (in rad/mm or cycles/mm), N phase images, ${\varphi }_i(\overrightarrow{r})$ can be obtained from a set of ${({\overrightarrow{k}}_e)}_i$ as follows:

$${\varphi }_i(\overrightarrow{r})={({\overrightarrow{k}}_e)}_i·\overrightarrow{u}(\overrightarrow{r}),i=1,2,\dots N.$$ (1)

Three-dimensional characterization of $\overrightarrow{u}(\overrightarrow{r})$ can be obtained from phase images encoded in orthogonal directions by, for example, letting $\underset{¯}{K}={[{({\overrightarrow{k}}_e)}_1\dots {({\overrightarrow{k}}_e)}_i]}^T$ and solving for the least squares problem given by [44]

$$\overrightarrow{u}(\overrightarrow{r})={({\underset{¯}{K}}^T\underset{¯}{K})}^{-1}{\underset{¯}{K}}^T{\varphi }_i(\overrightarrow{r}).$$ (2)

In practice, each phase image also contains a spatially dependent contribution, $\mathrm{\Delta }\varphi (\overrightarrow{r})$, due to instrumentation imperfections (e.g., magnetic field inhomogeneity) such that the phase image is more accurately represented as ${\varphi }_i(\overrightarrow{r})={({\overrightarrow{k}}_e)}_i·\overrightarrow{u}(\overrightarrow{r})+\mathrm{\Delta }\varphi (\overrightarrow{r})$. The influence of the background inhomogeneity term can be corrected by subtracting a phase image without displacement encoding, often called reference, from each of the encoded images prior to the application of (2). Thus, the measurement of a 3-D vector field via DENSE requires a minimum of four images: three motion-encoded images (often in orthogonal directions), and a nonencoded reference image [26].

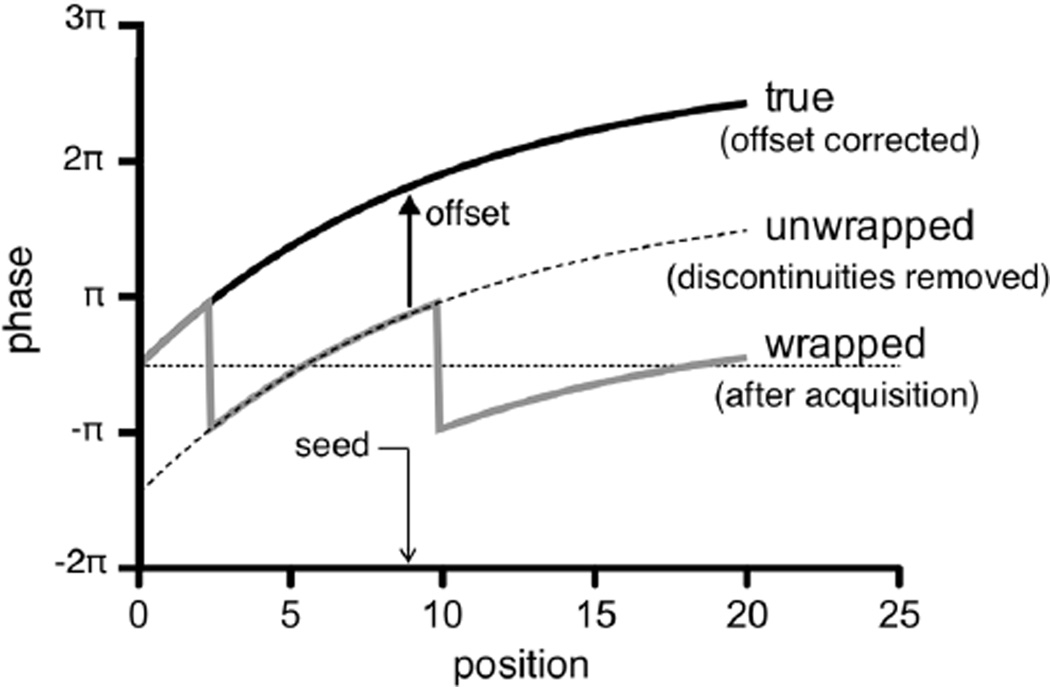
Because the phase quantity is periodic, phase wrapping occurs when the encoded phase exceeds its cyclic interval of 2π, say [−π, π] Fig. 1 shows examples of true and wrapped displacement profiles. Although part of the acquisition process involves empirically optimizing ${\overrightarrow{k}}_e$ to maximize resolution while minimizing phase wrapping, the latter remains unavoidable in practice especially when high spatial resolution is desired [45]. Consequently, a major part of displacement measurement via DENSE is the postprocessing of phase wrapped images, which involves two critical steps: first, the phase is unwrapped to eliminate discontinuities in phase images, and second, the resulting continuous phase maps is matched to true displacements by correcting for the phase offsets at selected pixels (known as “seed,” “true phase,” or “reference” points). Although phase unwrapping has been well studied from its association with other fields like radar interferometry [46], [47] and geophysics [48], [49], matching the results to underlying displacements is more unique to DENSE reconstruction, which continues as an active area of research [29], [45], [50].

Fig. 1.

Effect of phase wrapping in displacement profiles. The measurement of the true motion (black) is initially affected by phase wrapping (gray). Phase unwrapping effectively removes the discontinuities in the displacement profile (dashed line), but an offset vector evaluated at a seed location is necessary to fully reconstruct the original displacements.

Given a contiguous tissue region in a slice, the contribution of an phase offset error, (ϕ_e)_i, can be included by modifying (2) into

$${\overrightarrow{u}}_d(\overrightarrow{r})={({\underset{¯}{K}}^T\underset{¯}{K})}^{-1}{\underset{¯}{K}}^T{\varphi }_i(\overrightarrow{r})+{({\underset{¯}{K}}^T\underset{¯}{K})}^{-1}{\underset{¯}{K}}^T{({\varphi }_e)}_i=\overrightarrow{u}(\overrightarrow{r})+{\overrightarrow{u}}_{\mathit{\text{ref}}}$$ (3)

which shows that uncorrected phase offsets would result in an unknown, but constant offset error vector ${\overrightarrow{u}}_{\mathit{\text{ref}}}$ in the DENSE displacement field ${\overrightarrow{u}}_d(\overrightarrow{r})$ In the absence of any correction, errors in ${\overrightarrow{u}}_{\mathit{\text{ref}}}$ can dominate the displacement solution and can affect estimates of motion, rotation about a given axis, and through-plane strain measurements in multislice acquisitions or strain tensor polynomial fitting [51], [52]. Therefore, it becomes necessary to approximate the reference vector, for instance, by visual inspection. Alternatively, a priori knowledge of the tissue motion can also be used. For example, because healthy left-ventricular (LV) motion in a 2-D slice is mostly radially symmetric, it has been assumed that in-plane displacements should average to zero [26]. Offset vectors can also be estimated assuming small displacements in between frames [29], [45]. To date, means to objectively correct for arbitrarily fast or large displacements in between temporal frames remains lacking.

B. Image Registration and Hyperelastic Warping

A common strategy for nonrigid image registration consists of an optimization problem aimed at finding the deformation map, $\overrightarrow{\phi }$, that minimizes a fidelity measure between two images: a template image, $T(\overrightarrow{x})$, and a target (or source) image $S(\overrightarrow{X})$ [32]–[35], [37]. (The upper and lower cases, $\overrightarrow{X}$ and $\overrightarrow{x}$, are used here to identify coordinate systems before and after image registration, respectively.) Depending on their formulation and implementation, different registration processes may output the resulting deformation field as $\overrightarrow{\phi }:\overrightarrow{X}\to \overrightarrow{x}$, its inverse ${\overrightarrow{\phi }}^{-1}:\overrightarrow{X}\to \overrightarrow{x}$, or both. Because the proposed method involves pairing registration results with DENSE displacements, the resulting displacements must be expressed in spatial coordinates, $\overrightarrow{r}$, which can be obtained directly, by interpolation, or by switching the order of the input imagery depending on the registration algorithm.

In Hyperelastic Warping, $\overrightarrow{\phi }(\overrightarrow{X})=\overrightarrow{x}(\overrightarrow{X})$ is obtained via FE approximations [35], [36]. The resultant displacement field ${\overrightarrow{U}}_w(\overrightarrow{X})=\overrightarrow{X}-\overrightarrow{x}(\overrightarrow{X})$ (or ${\overrightarrow{u}}_w(\overrightarrow{r})$ in spatial coordinates) corresponds to translations of the FE nodes. Magnitude image information is used to drive a mesh towards deformation by means of

$$\overrightarrow{b}(\overrightarrow{X})·\overrightarrow{\eta }=\lambda \left(\right[T(\overrightarrow{X})-S(\overrightarrow{\phi })]\frac{\partial S(\overrightarrow{\phi })}{\partial \overrightarrow{\phi }}·\overrightarrow{\eta })$$ (4)

where $\overrightarrow{b}$ is equivalent to a body force field in the general direction $\overrightarrow{\eta }$, and λ is a factor that scales the contribution of image-based forces that, according to the FE solution approach, will be balanced by stresses associated with material properties (e.g., stiffness or bulk moduli) by means of conservation of momentum as detailed in [35], [36], [43]. To capture large displacements, it is customary to apply blurring to the images in the early stages of registration, and gradually reduced thereafter, which ensures local displacements are not impacted. The forcing term, (4), is equivalent to weighted pixel-wise intensity differences (i.e., the spatial gradient of the target image evaluated at stationary target points). While intensity differences provide a fidelity measure, the gradient component provides force scaling and directionality. In fact, the spatial gradient directs registration based on texture and edge information. Consequently, areas with no local intensity gradients do not contribute to registration forces [43].

To compensate for types of motion inherently difficult to capture using intensity images (e.g., rotation about an axis of symmetry), and for areas within an image far from object edges or without texture, Hyperelastic Warping can include physically realistic geometry, boundary conditions, and material constitutive information improve the accuracy of the results. Therefore, although Hyperelastic Warping has the advantage of capturing large displacements between frames, accuracy may be uniform, concentrated, or scattered, depending on additional compensatory information.

C. Proposed Reconstruction Strategy

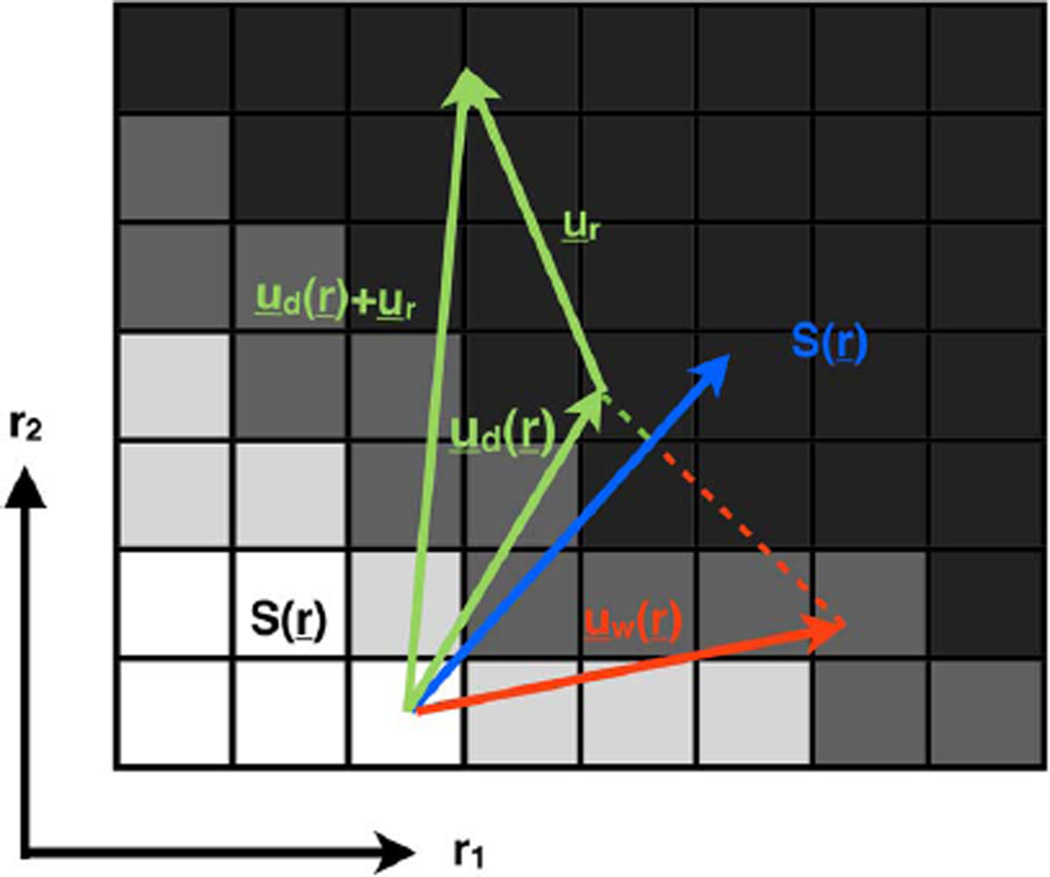
Two important observations can be made from the above discussion on DENSE and Hyperelastic Warping, that 1) each component of a given displacement can be measured from DENSE except it may contain a contribution from erroneously determined phase offset, and 2) in the absence of additional information, the confidence of the measured displacement via Hyperelastic Warping is highest in areas where image contrast is highest, since these locations have the large image-based forces as quantified via (4). As illustrated in Fig. 2, these two observations lead to the unique criterion that correct solutions to DENSE and Hyperelastic Warping estimations of displacement should be identical along the direction of the image intensity gradient, which constitutes a measure of local contrast. In other words

$${\overrightarrow{u}}_d(\overrightarrow{r})·\nabla S(\overrightarrow{r})={\overrightarrow{u}}_w(\overrightarrow{r})·\nabla S(\overrightarrow{r})$$ (5)

where $\nabla S(\overrightarrow{r})=\partial S(\overrightarrow{r})/\partial (\overrightarrow{r})$, is the intensity gradient of the image acquired after the deformation has occurred with respect to spatial coordinates. The basic premise of the current work is that image registration information, readily obtainable from images already included in the DENSE acquisition, can be used via (5) to regularize DENSE reconstruction such that accurate displacement fields can be obtained.

Fig. 2.

Schematic illustration of the proposed registration-enhanced dense reconstruction. The grid represents a zoomed view of the deformed image $S(\overrightarrow{r})$, which is defined in spatial coordinates, $(\overrightarrow{r})$. Because intensity-based registration solutions, ${\overrightarrow{u}}_w(\overrightarrow{r})$, are more accurate in areas with greater local contrast, the gradient, $\nabla S(\overrightarrow{r})$, is used as a weight for the comparison to dense solutions, ${\overrightarrow{u}}_d(\overrightarrow{r})$. An offset ${\overrightarrow{u}}_r$ is found so to minimize the difference between components parallel to the gradient. In that way, the dense solution may retain displacements in directions that are not perceptible by the registration process.

In practice, (5) can be implemented in DENSE reconstruction by inserting (3) and rearranging, which yields the solution for the offset error vector given by

$$\nabla S({\overrightarrow{r}}_j)·{\overrightarrow{u}}_r=[{\overrightarrow{u}}_w({\overrightarrow{r}}_j)·\nabla S({\overrightarrow{r}}_j)-{\overrightarrow{u}}_d({\overrightarrow{r}}_j)·\nabla S({\overrightarrow{r}}_j)]$$ (6)

wherein every pixel in a slice, j = 1, 2,… M, provides an equation in a linear system that can be solved using weighted least squares. If a 3-D unwrapping algorithm is used [53], then (6) can be applied along a volume instead of a slice region effectively reducing computation time. It should be noted that the offset error vector ${\overrightarrow{u}}_r$ is defined in (3) for a contiguous region, and different contiguous areas (e.g., the heart and chest within a given MR image) may have different offset vectors. To solve this problem, and to better capture relative motion or other interactions, (6) can be applied to subregions of a volume by means of region-specific masks.

The above formulation of combined displacement field reconstruction should be flexible enough to allow [(5) and (6)] to be implemented with alterative registration techniques other than Hyperelastic Warping. Gradient-based forcing terms similar to (4) arise from minimization of a generalized fidelity measure of image intensity energy, namely

$$E(\overrightarrow{X},\overrightarrow{\phi })=\frac{\lambda }{2}{(T(\overrightarrow{X})-S(\overrightarrow{\phi }))}^2$$ (7)

which assumes a Gaussian distribution for MRI intensity [54]. Actually, (4) becomes apparent from the first variation of (7) with respect to $\overrightarrow{\phi }$ A similar minimization strategy is the basis of alternative registration formulations, including some forms of fluid and diffusion registration [32], [34], [55].

III. Methods

The validity, effectiveness, and practical feasibility of the proposed approach were assessed using a combination of numerical and experimental procedures. Testing was based on fast dynamics characterized by large deformations between temporal frames, which result in significant phase wrapping. The numerical procedures involved quantifying measurement errors across different simulated scenarios that might be impractical to reproduce experimentally. The experimental procedures were aimed to confirm observations from simulated scenarios, and demonstrate the usage of the technique in vivo.

A. Numerical Verification

Two sets of computer simulations were performed: the first included different deformation scenarios, and the second consisted of a basic sensitivity analysis aimed to elucidate the effects of practical parameters on the accuracy of results.

1) Numerical Phantom and Image Generation

Volumetric images from a synthetic object (see top of Fig. 3) were created using a 50×50× matrix size. In order to capture a wide range of displacement magnitudes and directions, three deformation scenarios were used to warp the initial images, and generate simulated phase images. The deformations consisted of 1) simultaneous 20% stretch along the first in-plane axis (here referred as the x-axis) and 30% compression along the perpendicular in-plane direction (y-axis), which corresponded to a homogeneous deformation without through-plane components, 2) 10% compression along the z-axis, with a 10-pixel translation diagonal to x, y, and z, which was chosen to represent mostly rigid motion, and 3) contraction by three pixels in all directions with simultaneous 20 rotation about the z-axis. Depending on the location, displacements generated ranged from 0 to approximately 20 pixels in virtually all directions. To focus on the accuracy of deformation estimation without potential complication from noise, the images were generated with an SNR of 500.

Fig. 3.

Numerical phantom and images used for verification. A thick-walled glyph (top) was used to generate testing images under various applied deformations. Examples of before (bottom left) and after (bottom right) images under the deformation (bottom center) described in scheme (c) of the text are shown.

Whereas the input images for registration consisted of the original and deformed states of the numerical phantom, complex DENSE images encoding the deformations information were simulated, with the corresponding displacements encoded in the wrapped phase angle given by

$${\varphi }_i(\overrightarrow{r})=\text{mod}(\frac{\pi }{u_i^{\mathit{\text{max}}}}{\overrightarrow{u}}_i(\overrightarrow{r})-\pi ,2\pi )-\pi$$ (8)

where mod stands for the modulo operator, and $u_i^{\mathit{\text{max}}}$ indicates the maximum displacement before phase wrapping, set at two pixels in the in-plane directions, and one pixel in the out-of-plane direction. The maximum limit was chosen partly based on empirical observations, and partly to ensure nearly all images were affected by phase warping artifacts.

2) Displacement Field Reconstruction

To represent the measurements obtained by each of the approach described in Section II, displacement fields were reconstructed using Hyperelastic Warping (subsequently referred to as registration solution), DENSE with offset correction for bulk motion of the imaged object (bulk corrected solution), and the proposed approach combining DENSE and Hyperelastic Warping (combined solution).

3-D Registration was performed using a validated implementation of Hyperelastic Warping in NIKE3D software [56]. The registration code was embedded in a MATLAB (Math-works, MA, USA) script, which automatically generated an FE model, determined image blurring, and optimized the registration parameter λ from (4) according to the following: The FE model consisted of hexahedral elements with nodes coinciding with pixel locations, assumed to behave as an isotropic Neo–Hookean solid [57] with coefficients C₁=8 KPa and bulk modulus of κ.= 0.1 KPa The initial size of the blurring mask was made to be a fixed 20% of the average number of pixels in each dimension. Because material coefficients were arbitrary, given that the maximum agreement between two images was obtained following convergence with the highest registration parameter, λ, the latter was optimized according to convergence so that maximum registration was achieved. The optimization began with a small value for λ (0.1), which was then increased if the registration process converges, or vice versa by means of bisection. To obtain a displacement field in the same coordinate frame as the DENSE results, all registration was done using the absolute reference configuration as the target, and subsequent images as the template.

For DENSE reconstruction, each image slice was first unwrapped as previously described in [58]. To approximate the phase offset without using registration, a bulk motion displacement was defined as the translation of the synthetic object’s centroid from before and after deformation. In contrast, for the proposed approach, essentially the same DENSE reconstruction was performed except registration information was used to correct for the phase offset via (6), which was evaluated at every slice.

3) Performance Assessment

With the displacements used to generate the input images as ground truth, the accuracy of the three solutions was evaluated based on percent absolute length and angular differences at each voxel (e.g., if a vector was 1.3 times the magnitude, and perpendicular to the true vector, then the errors would be 30% and 90°, respectively). Error values were averaged across the volume and reported along with their standard deviation. Finally, to provide insight on deformation calculations, the principal components of the Green–Lagrange strain tensor were computed using a finite-difference deformation gradient approximation and eigenvalue decomposition [59].

4) Sensitivity Analysis

The experiments created as a sensitivity analysis included variations in noise levels, warping parameters, and compatibility of the proposed method with other registration approaches. These tests included: 1) signal-to-noise ratio (SNR) variations (500, 100, 50, and 15), 2) changes in registration parameters, with C₁ and bulk modulus decreased or increased by50% (0.5C₁, 1.5C₁, 0.5κ, and 1.5κ), and 3) replacing the registration algorithm with automatic, nonrigid technique delineated in [55] instead of Hyperelastic Warping. In each of these cases, the combined solution displacement fields were obtained for all deformation scenarios and compared to the ground truth as described above. The performance was averaged for the three deformation scenarios and reported.

B. Validation With Experimental Phantom

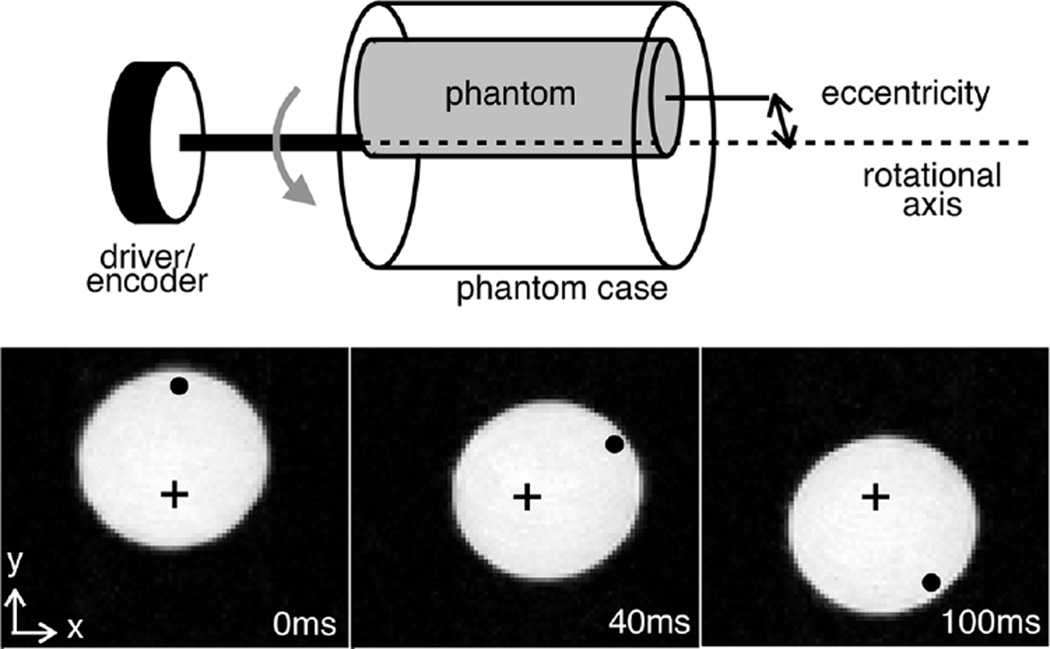
Based on previously documented DENSE-MRI studies such as [60], a precision apparatus was designed to move a phantom along a predictable path, which served as a benchmark displacement field. The motion of the phantom was designed to both, induce phase wrapping since the initial time frame, and include displacement in a direction without local contrast. To achieve these goals, the rotational speed was set to produce motion beyond the wrapping interval, and the phantom was constructed with a substantial lack of internal contrast.

1) Motion Apparatus

A phantom consisting of a cylindrical container 16 mm in diameter filled with a water-based gel (1.0 mg/L CuSO₄ in 2.0% Agarose) was mounted to a case inside the MRI bore (Fig. 4, top). The case was rotated by an externally positioned motor at a rate of 4 rev/s, which ensured phase wrapping of all images. An optical encoder was used to provide angular speed and position monitoring, as well as acquisition triggering. The phantom was eccentrically placed within the rotation apparatus, and slices were chosen so that the trajectory, a combination of bulk motion and rotation, could be described analytically as follows. Given a rotation matrix Q

$$\underset{¯}{Q}(\theta )=\left[\begin{array}{cc}\mathit{\text{cos}}\theta & \mathit{\text{sin}}\theta \\ -\mathit{\text{sin}}\theta & \mathit{\text{cos}}\theta \end{array}\right]$$ (9)

and the identity matrix I, the displacement field can be defined as

$$\overrightarrow{u}(\overrightarrow{r},\theta )=(\underset{¯}{I}-\underset{¯}{Q}(\theta ))\overrightarrow{r}$$ (10)

where the angle of rotation, θ, is proportional to the rotational velocity and multiples of the repetition time at each frame.

Fig. 4.

Schematic and MR images of the controlled motion apparatus. The schematic (top) shows the location of the phantom with respect to the rotation apparatus. The trajectory of the object can be obtained either from imaging data or from the encoder output and eccentricity measurement. To visualize the motion, the magnitude MR images (bottom) are overlaid with the approximate location of the axis of rotation (+), and a point near the edge of the phantom(•) as time progresses.

2) Imaging Parameters and Image Preparation

The moving phantom was imaged using a CINE DENSE pulse sequence [26] on a Bruker Biospec 7T scanner (Bruker Biospin, MA, USA), and a 72-mm ID quadrature volume coil. Other pertinent imaging specifications included 20.0 ms TR, 2.0 ms TE, 40 × 40 mm FOV, 96 × 96 matrix size, and 0.7 cycles/mm motion encoding gradients in each x and y directions. DENSE magnitude images (i.e., mages after k-space subtraction and low pass filtering), obtained in all displacement encoding directions were averaged to compensate for stimulated echo signal loss, and then used as input to the registration algorithm.

3) Displacement Field Analysis

Equation (9) served as the ground truth to which image-based motion measurements were compared. The error analysis and reconstruction approaches were identical to the numerical verification steps described above. Additionally, to assess displacement field quality in terms of pixel correspondence across time points, intensity differences between the images at time zero and material point evaluations of images at later times (i.e., using deformation field to effectively move the image back to the original configuration) were also reported in maps and as root-mean-squared (rms) difference measured in arbitrary units (a.u.). To calculate the center of rotation used for the benchmark displacement field, the best center points at each time frame (per rms minimization) were averaged assuming that the center of rotation does not change in time. Differences in vector fields resulting from using the mean and the best center rotation for each time point were averaged to estimate this uncertainty.

C. In Vivo Experiment

Cardiac imaging was selected as the means for in vivo demonstration of the combined methodology to test whether general practical challenges (e.g., the usage of gradients or practical SNR) are fundamental impediments to its application, and if controlled experiment results are able to carry over to an in vivo setting. The resulting displacements were compared to manually tracked tags, systolic twist angles and circumferential strains were compared to previous studies [59], [61]. Each result compares a reference configuration, end diastole (ED), to subsequent time points. No intermediate data is used to obtain a given result.

1) Animal Protocol

All animal protocols were approved by the Institutional Animal Care and Use Committee at the University of Utah in accordance to the Guide for the Care and Use of Laboratory Animals issued by the US National Institutes of health (NIH Publication No. 85–23, rev. 1996). An adult male (350 g) Sprague Dawley rat was anesthetized with 1%–3% isoflurane and 0.8 L/min O₂ For imaging, the animal was placed prone inside the RF coil. Vital signs (respiration, temperature, heart rate ECG, and oxygen saturation) were continuously monitored using a MR-compatible physiological monitoring system (SA Instruments, Stony Brook, NY, USA).

2) MRI Acquisition

The DENSE pulse sequence described in the previous section was applied in four cardiac short axis slices including the ventricles, ribs and surrounding tissue. Image acquisition was double-gated (to respiration and ECG) to start at beginning systole (t = 0) and continue with 20 ms frames (i.e., 50 frames/s) thereafter. To provide a qualitative comparison of the results, tagged MRI images [16] (with 2 mm tag spacing) were also acquired in the same slice locations.

3) Displacement Reconstruction and Deformation Analysis

An average of the magnitude DENSE displacement-encoded images was registered using the simplified application of Hyperelastic Warping described above. Images at each cardiac time point were registered to the image at t = 0, so that results were not dependent on temporally adjacent images. Displacement fields within a segmented region of the LV myocardium were obtained using (9), unwrapped DENSE phase images, and the registration solution. For comparison, additional displacements at select locations around the LV were also obtained by manual tracking of tag intersections using customized interactive software. Lastly, to illustrate the utility of the displacement measurements, circumferential strain and mid-ventricular longitudinal shortening, (approximated by the average principal strain closest to the circumferential and through-plane directions, respectively), as well as slice twist, and left-ventricular torsion were also recorded for comparison with previously published values of a healthy rat [59], [61].

IV. Results

A. Numerical Simulations

1) Reconstruction of Displacement Vector Fields

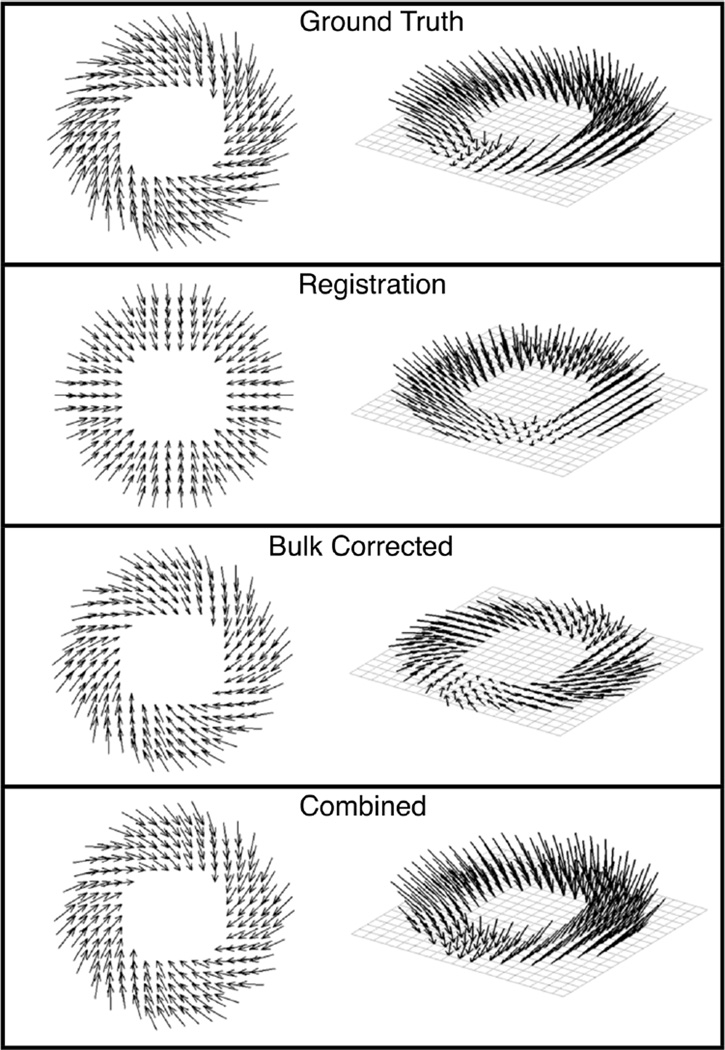
The displacement vector fields obtained for a representative image slice under test deformation scenario (c), where there existed a large variability in the performance among the different estimation schemes, is shown in Fig. 5. Compared to the ground truth, it can be seen that the bulk motion-corrected technique conspicuously underestimated the through-plane displacements included in deformation scenario (c), in agreement with the known limitation of the technique for the particular type of motion examined. Similarly, the registration-based method was largely unable to capture the prescribed rotational motion. In contrast, the proposed approach performed much better in characterizing the displacements under identical circumstances.

Fig. 5.

Displacement vector fields obtained by the different schemes for deformation scenario (c). The deformation consisted of rotation within the imaging plane as well as contraction in all axes. The vector fields estimated for a single slice are shown as viewed from above (left column) and obliquely (right) to highlight the in-plane and through-plane components of the motion, respectively.

The performance of the different reconstruction schemes, in terms of quantified errors in the measured displacements, under different deformation scenarios are listed in Table I. Consistent with the above observations, the proposed combined approach outperformed the registration and bulk motion-corrected schemes under all scenarios tested resulting, in some instances, in magnitude error reductions of approximately 75%, 50%, and 66% [i.e., with respect to registration alone in case scenario (a), and bulk correction alone in scenarios (b) and (c)] On the other hand, the registration solutions performed rather poorly, likely because the simulation phantom lacked internal contrast and was thus biased against the scheme. Overall, the performance of all schemes was best when the deformation was limited to the imaging plane under scenario (a), and progressively deteriorated when through-plane and rotational motion were introduced in scenarios (b) and (c).

TABLE I.

Mean Error in Displacement Estimations Under Different Deformation Conditions

	Scenario (a) Stretch (x) Compression (y)	Scenario (b) Rigid Motion Compression (z)	Scenario (c) Contraction and Rotation
Registration	21 ± 12%	20 ± 24 %	26 ± 4.7 %
	9.5 ±5.3°	14 ±7.6°	33 ± 6.0°
Bulk	7.3 ± 7.4 %	29±15%	31 ±9.4%
Correction	7.8 ±3.2°	24 ±19°	24 ± 11°
Combined	5.5 ± 4.9 %	14 ±4.5%	11 ± 7.4 %
Method	4.6 ±1.8°	5.4 ± 3.4°	8.4 ± 3.1°

Entries correspond to the mean and standard deviation of vectorial error in percent magnitude and angular differences from the ground truth.

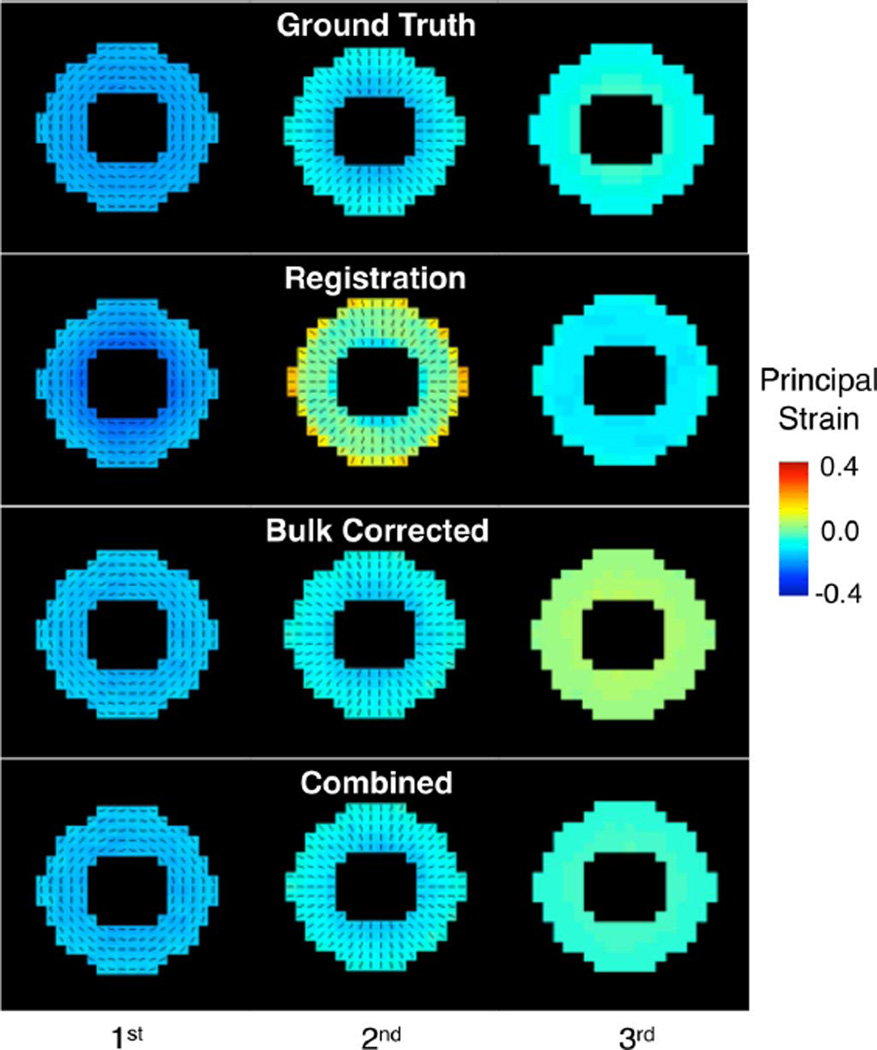
Simulated strain results in Fig. 6 correspond to the same slice seen in Fig. 5 where the principal strain components align with the circumferential, radial, and axial directions. The registration solution offers adequate agreement in principal directions and mean circumferential and through-plane strain, but there are discrepancies in radial strains likely due by concentration of registration forces near the borders, which result in over-estimation of radial deformation. Because strains were calculated using relative motion, bulk correction results are unaffected by offset in the in-plane direction, but, because the average though-plane motion of the slice is different than the bulk motion of the volume, bulk correction fails to accurately approximate local strain in that direction. Similar observations were made in test scenario (b), but not in scenario (a) since through-plane deformation in that case was rigid (not shown). Finally, The combined method was able to better capture deformation, as well as displacement and rotation, in all directions.

Fig. 6.

Strain maps obtained by the different schemes for deformation scenario (c). Circumferential, radial, and through plane (longitudinal) strains are respectively represented by the first, second, and third principal strains. Except for the, through-plane, direction the principal strain directions are shown in black lines.

2) Sensitivity Analysis

The performance of the presented approach with respect to variations in SNR is shown in Table II, which contains errors averaged across all displacement scenarios investigated. Compared to the case of SNR of 500 (essentially noiseless), the method performed consistently and accurately within the range of practical SNR values (50–200) despite moderate noise. The consistency can be attributed to the use of smoothing in Hyperelastic Warping and the inherent robustness of phase imagery in DENSE. Not unexpectedly, the error of the method became noticeably increased at the lowest case, SNR = 15.

TABLE II.

Performance of the Proposed Displacement Measurement Approach as a Function of Image SNR

SNR	500	200	50	15
Error	10 ±4.7%	10 ±4.6%	10 ±4.6%	17 ± 10%
	6.1 ±2.2°	6.0 ± 2.2°	6.1 ±2.2°	10 ±5.6°

Entries correspond to the mean and standard deviation of vectorial error in percent magnitude and angular differences from the ground truth.

The effects of variations in the material coefficients used in Hyperelastic Warping on the performance of the proposed combined method are shown in Table III. The performance is shown to be relatively stable across the range (50%–150%) of the stiffness parameter C₁ and bulk modulus κ investigated, with the exception that slightly elevated errors were observed when higher κ was used. The relative insensitivity to C₁ is indicative of the effectiveness of the penalty parameter λ optimization, which reduces the dependency on material assumptions. In contrast, the increased error associated with higher κ is likely due increased resistance to changes in volume.

TABLE III.

Mean Error With Respect to True Displacement Field for All Deformations With Registration Parameter Variations

Parameter Change	0.5C1	1.5C1	0.5κ	1.5κ
Error	10± 5%	10 ± 5%	10±6%	15 ±6%
	6.1 ±2.2°	6.1 ±2.3°	7.7 ± 3.7°	7.5 ±5.1°

Entries correspond to the mean and standard deviation of vectorial error in percent magnitude and angular differences from the ground truth.

Lastly, replacing Hyperelastic Warping with the fundamentally dissimilar nonrigid registration technique resulted in averaged percent magnitude and angular errors (across all deformation scenarios) of 6.1 ± 9.4% and 5.7 ± 7.0°, respectively, which are comparable to those for Hyperelastic Warping, 10 ± 4.7% and 6.2±2.2°. The option to use an alternative registration method is attractive when Hyperelastic Warping is unavailable or for whatever reason not applicable.

Most computational time was used for the registration step, which given its iterative nature varied from 3 m to 1 h. Application of (6) increased computation time by a few seconds, which were needed to process the entire volume.

B. Validation Using Experimental Phantom

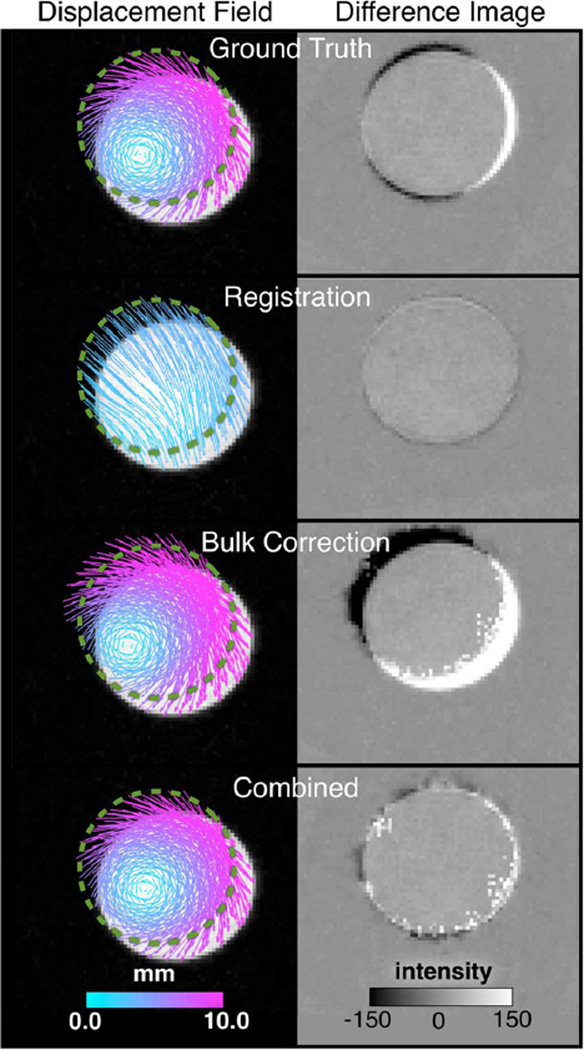
Fig. 7 contains representative images obtained for the rotating phantom, as well as corresponding displacement fields estimated by the different schemes. Based on error with respect to the ground truth averaged over all time points, the three displacement measurement approaches compare as follows: While image registration provided excellent match between the acquired and reverse-estimated images of the phantom at initial position and yielded a low average rms of 0.2 ± 1.3 a.u. across time points, it was largely unable to describe the phantom’s internal rotation resulting in high vectorial percent magnitude and angular errors of 56 ± 82% and 57 ± 46°, respectively. The DENSE field corrected by bulk displacement approximation revealed a conspicuous offset in the image difference, which translated to quantified errors of 1.6 ± 6.6 a.u., 23 ± 31%, and 9.0 ± 14°. By correctly estimating the offset, the proposed approach generated the most accurate displacement measurement, with the corresponding errors reduced to 0.6 ± 2.8 a.u., 7.2 ± 12%, and 4.7.± 6.9°. The relatively poor performance of the registration method was expected, given the phantom’s lack of internal texture, which can be compensated by tags [62], material properties [42], [43], or the inherent nature of DENSE provided adequate correction of offset bias [63]. In reconstruction schemes involving DENSE (i.e., the bulk motion-corrected and proposed combined methods), the effects of image noise can be seen in the jagged border of the reverse-estimated initial-position image. However, the noise appeared not to have adversely impacted the displacement estimations.

Fig. 7.

Experimental validation measurements on the rotating phantom. The left column shows prescribed (ground truth) and measured displacement vector fields superimposed on the axial image of the phantom at t = 40 ms according to the description in Fig. 4. The green dashed line delineates the edge of the phantom at t = 0. The right column shows intensity difference images between actual and reverse-estimated initial location of the phantom.

It is worth noting that the benchmark displacement field resulted in a small but visible discrepancy in the difference image (Fig. 8 top), which is due to the unavoidable disparity between the prescribed and actuated motions. The errors associated with the disparity were 0.41 ± 1.56 a.u., 1.6 ± 2.2%, and 0.9 ± 1.1°, which fall well below those of any scheme investigated and provides justification for the field obtained by (9) to be used as the ground truth.

Fig. 8.

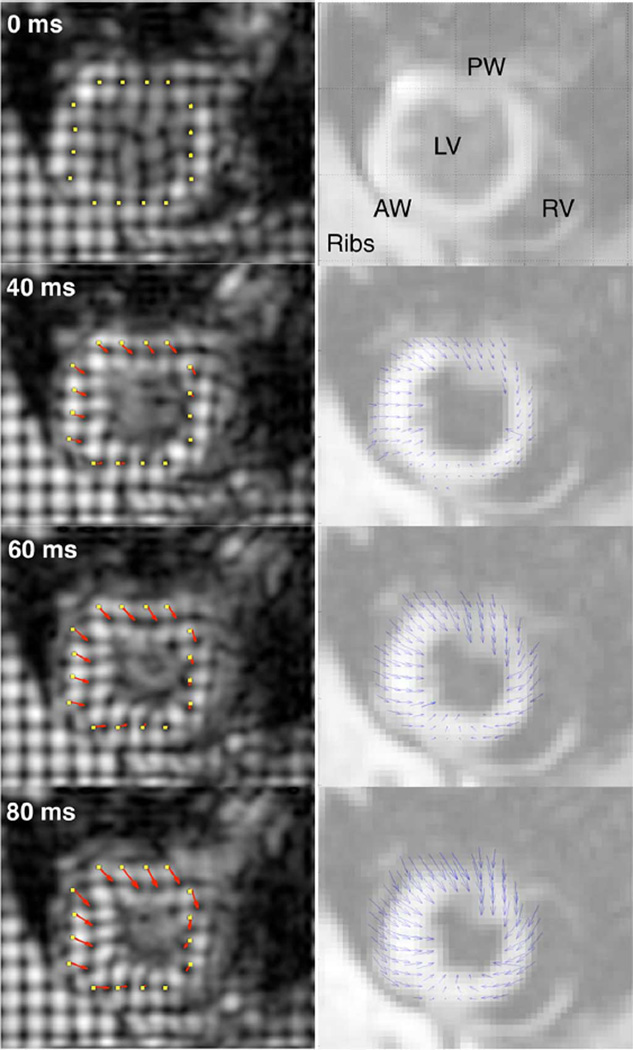
Tissue Displacements by tagging and registration-enhanced DENSE. Sixteen reference points (yellow dots) placed around the LV myocardium on the tagged images (left column) were manually tracked to yield displacements (red arrows). DENSE vector plots (blue arrows) are overlaid on intensity-scaled magnitude images (right column). RV and LV indicate right and left ventricle, respectively. AW and PW stand for anterior and posterior walls. For clarity, only half the vectors in the registration-enhanced DENSE field are shown.

1) In Vivo Demonstration

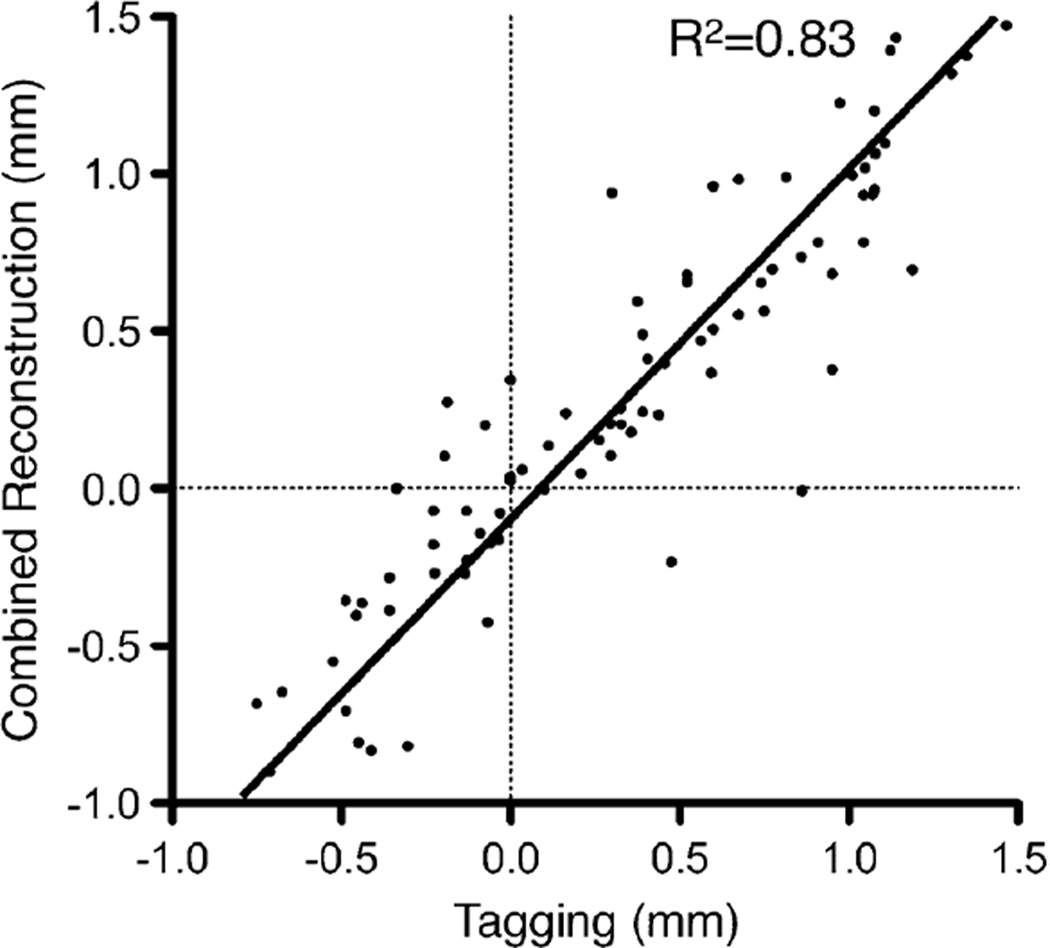
Fig. 8 shows the displacements of the LV myocardium measured in a slice near the cardiac base as the rat’s heart deformed from ED towards end systole (ES). In general, as observed with both tag tracking and registration-enhanced DENSE, the movement of the myocardium from ED to ES exhibited the familiar wall thickening and cavity reduction associated with LV contraction. The anterior part of the septum was relatively stationary, and most displacement occurred in the LV free wall. The above observation is consistent with visual inspection with respect to the anterior portion of the ribcage, which remains relatively stationary throughout the imaged time points likely due to the animal’s prone orientation, as body weight presses the sternum against the bed. Additionally, qualitative interpretation of Fig. 8, and comparison of in-plane motion across different slices in Fig. 9, both show good agreement between the displacement fields obtained by tag tracking and the proposed method. The computational time needed for registration and combined reconstruction of in vivo data averaged 30 m.

Fig. 9.

Direct comparison of displacements obtained by the proposed technique and tagging. Each point corresponds to a component-by-component comparison of in-plane displacements at same locations at t = 80. R2 indicates coefficient of determination.

A rendering of the 3-D LV motion at ES constructed from displacement fields obtained in multiple slices is shown in Fig. 10. In contrast to the above noted variability of displacements within the imaging plane, the through-plane motion was relatively uniform, in agreement with previous observations of animal cardiac motion [64], [65]. From the 3-D displacement fields, the LV twist angles were measured to be −3.0 ± 3.0° (mean ± SD for the slice), 2.8 ± 3.2°and 8.9 ± 3.8° at the base, mid-ventricle and apex, respectively. These values are similar to the −5.6 ± 1.9° and 9.0 ± 2.3° reported previously for the base and apex, respectively [59].

Fig. 10.

Multi-slice Reconstruction of 3-D Left-Ventricular Motion. The color indicates the magnitude of the vectors. Despite of the though-plane motion, the total motion in the anterior wall (AW) near the septum separating the left and right ventricles, (LV and RV, respectively). The largest displacements occur in near the posterior wall (PW).

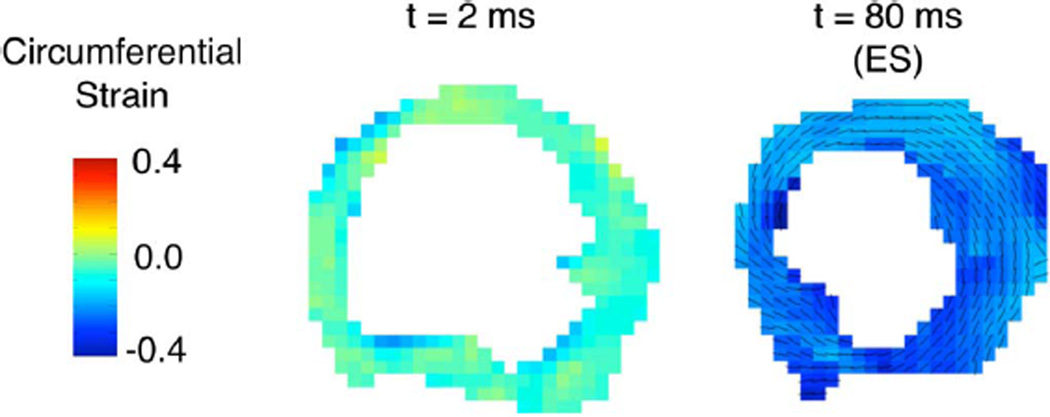
Also based on the estimated displacement fields, the systolic LV circumferential strain was found to be − 0.16 ± 0.08 (slice mean ± SD), −0.19 ± 0.06, and, −0.23 ± 0.04 at the base, mid-ventricle, and the apex, respectively, which are in excellent agreement with values of − 0.16 ± 0.02, −0.19 ± 0.01,and −0.21 ± 0.01 reported previously for the same measurements [59]. Mid-ventricular shortening was measured at −15 ± 4%, which also compared very well with previously reported values of −16 ± 3% [61]. Fig. 11 shows the unsmoothed circumferential strain maps from displacement fields obtained using the proposed technique acquired shortly after ED and at ES. The reduction in strain magnitude from approximately zero (as some contraction took place during the mixing time in the DENSE pulse sequence) at ED towards the negative systolic strain was relatively uniform, indicating that the deformation was evenly distributed across the myocardium, including regions where absolute displacement was near zero.

Fig. 11.

Circumferential strain maps in the rat LV myocardium. Compared to its value near end diastole(t = 2 ms), end-systolic (ES) strain indicates tissue shortening along the circumferential direction (black lines), which in contrast to the displacement field, occurs relatively uniformly across the entire myocardium despite a nonuniform displacement field (Fig. 8).

V. DISCUSSION

Overall, results of the numerical simulation, empirical phantom and live animal demonstration experiments shown in Figs. 5, 7, 8, and 9, and Tables I–III, are strongly supportive of the basic premise of the current study, that image registration can be used to enhance the accuracy of DENSE displacement field mapping. As explained in the Methods section, the accuracy of DENSE reconstruction critically depends on the ability to match unwrapped image phases to the underlying motion to eliminate cyclic phase offsets. The phase offsets are conventionally determined and corrected manually at only selected seed point locations using presumed displacement values. The excellent performance seen in the proposed approach can be attributed to the fact that via image registration it essentially employs all tissue borders (i.e., locations of high intensity gradient) as seed points and assigns them with actually measured displacements.

Besides the technical advantages, the proposed registration-enhanced DENSE reconstruction also offers some practical benefits. The approach uses images already in the dataset for its registration step, in as few as two time points, which reduces the need for intermediate acquisitions or other additional data. Moreover, because the reconstruction can estimate and correct the phase offsets with high degree of accuracy under a wide range of conditions, there is more flexibility in choosing the displacement encoding parameter (i.e., κ_e ) for the DENSE acquisition. Higher values can be desirable for encoding small displacements or resolving small displacement differences without the concern that at the same time larger displacements would be undermined by phase offset determination. The enhanced sensitivity and expanded encoding range can be potentially significant in characterizing functional remodeling associated with diseases where tissue deformations can be both subtle and inhomogenous.

The proposed displacement measurement scheme also facilitates post-acquisition reconstruction. Although accurate DENSE displacement measurements are attainable in theory, subjectivity error may be introduced in instances where offset estimations requires visual inspection. In contrast, the proposed scheme can accomplish the necessary phase offset correction largely free of user input or assumption of motion, and thus eliminate major sources of subjectivity and error in DENSE reconstruction. The present implementation of the reconstruction scheme requires only a small degree of user interaction, in defining contiguous regions of the tissue or organ in question. However, it is not inconceivable that the process can be made fully automated by incorporating more sophisticated image analysis methods, though such endeavor is outside the scope of the current investigation.

The current work is neither the first nor likely the last to improve the DENSE reconstruction accuracy via registration or other empirical means of motion estimation. In recent studies on cardiac mechanics [3], [29], [44], first-order approximations of velocity were used to estimate small deformations in intermediate DENSE scan time points. The deformation fields were then incorporated in the DENSE reconstruction to improve the accuracy tracking and phase offset determination [27]. Although a direct comparison may yield comparable performances, as noted above, the current direct registration-based reconstruction can be advantageous since it does not require 1) additional high temporal-resolution scans, or 2) the condition that the local deformations between frames to be small enough to be approximated by a first order velocity integration. Without these constraints, the proposed approach is better suited for characterizing deformation that involve relatively fast motion (or large displacement with respect to the scan intervals) or wide range of motions.

Needless to say, the proposed approach is not by any means perfect, especially in its dependence on image registration. Because of the complexity and heterogeneity of deformations found in tissues, no image registration is truly accurate for all situations in reality. Though the presented implementation and (5) itself minimize the effects of the deformation model used and the lack of trackable local intensity contrast, the accuracy of image registration is still influenced by the pixelation of tissue borders, which is dependent on the spatial resolution of the images. In the present study, these factors are likely responsible for the small but nonzero displacement measurement errors incurred by the proposed technique under near-ideal (e.g., numerical simulation with high SNR) testing conditions. Additionally, related to the effect of image resolution, the ability of the proposed approach to track through-plane motion is dependent on the number and thickness of the image slices in the dataset. Due to experimental considerations, the slice thickness in an MRI scan is usually coarser than the in-plane resolution, resulting in poorer performance of the technique in characterizing through-plane motion. An extreme limiting case can be conceptualized by an inhomogeneous motion of a cylinder without local contrast in the z-direction, which would result in the left-hand side of (3) being zero and the inability to solve (4). In this case, compensatory information, like stiffness gradients, may be necessary to achieve an accurate result. Despite these practical limitations, it should be noted that the proposed scheme combining registration and DENSE reconstruction still resulted in accuracy improvement in the investigated scenarios. Through-plane motion characterization, or other organ-specific dynamics, can be optimized by careful study, design, and scan prescription to achieve a desired level of repeatability and reproducibility before testing a biological hypothesis.

Finally, although designed to correct for DENSE additive phase offsets for a demonstration within cardiac kinematics, the proposed methodology may be furthered in several ways. As a start, instead of tuning Hyperelastic Warping towards automation (i.e., material parameter or geometry independence), as was done in the current study, it can be adjusted to include adequate geometrical, material, and load characterization [4], [42], [43], [66] to deliver a much more comprehensive mechanical analysis, like approximation of fiber shortening and stress. Such approach may be susceptible to element inversion, which was avoided here by allowing volumetric deformation, but can also be addressed with suitable material characterization including fiber directionality and active contraction. Moreover, the regularization criterion stated in (5), plus a parameter-driven minimization of the image energy equation in (7), can be used to correct for other types of uncertainty besides DENSE phase offsets. For example, rather than using an additive model specified in (3), a multiplicative or combined (additive and multiplicative) model may be constructed to better model the effects of phase accumulation resulting from the individual contributions and interactions among displacement-encoding and other imaging gradient pulses, such as slice refocusing, or spoiler pulses. Similar strategies involving the comparison of results via (5) can be used for phase unwrapping, scaling, and confidence analysis. For example by using information from registration for constraining the unwrapping problem, or vice versa. Beyond DENSE, registration-based phase correction can be extended to other types of MRI like velocity imaging [23] where the phase contrast needs to be accurately related to the underlying motion. In terms of applications, the present approach can be employed to improve the utility of DENSE or other MRI characterization of motion where the measurement is technologically limited, like in the study of impact mechanics [8], and large deformation characterization [1], [23]. All of the above can be worthy directions of future work.

VI. Conclusion

Tissue deformation imaging via DENSE offers the benefit of pixel-level measurements, but has been hampered in practice by the necessary phase unwrapping, and more importantly, phase offset determination. The current study introduced a method for reconstructing DENSE displacement field by making use of image registration information as an alternative for a priori assumptions, visual inspection, or separate scans to estimate motion to compensate for the phase offset uncertainty. Numerical and empirical phantom testing and demonstration on a live animal showed the approach to be highly accurate, automated, robust and compatible with 3-D displacement fields. These findings are very promising for incorporating the proposed registration enhancement to improve the practical utility of DENSE.