Comparison of Statistical Tests for Group Differences in Brain Functional Networks

Abstract

Brain functional connectivity has been studied by analyzing time series correlations in regional brain activities based on resting-state fMRI data. Brain functional connectivity can be depicted as a network or graph defined as a set of nodes linked by edges. Nodes represent brain regions and an edge measures the strength of functional correlation between two regions. Most of existing work focuses on estimation of such a network. A key but inadequately addressed question is how to test for possible differences of the networks between two subject groups, say between healthy controls and patients. Here we illustrate and compare the performance of several state-of-the-art statistical tests drawn from the neuroimaging, genetics, ecology and high-dimensional data literatures. Both real and simulated data were used to evaluate the methods. We found that, Network Based Statistic (NBS) performed well in many but not all situations, and its performance critically depends on the choice of its threshold parameter, which is unknown and difficult to choose in practice. Importantly, two adaptive statistical tests called adaptive sum of powered score (aSPU) and its weighted version (aSPUw) are easy to use and complementary to NBS, being higher powered than NBS in some situations. The aSPU and aSPUw tests can be also applied to adjust for co-variates. Between the aSPU and aSPUw tests, they often, but not always, performed similarly with neither one as a uniform winner. On the other hand, Multivariate Matrix Distance Regression (MDMR) has been applied to detect group differences for brain connectivity; with the usual choice of the Euclidean distance, MDMR is a special case of the aSPU test. Consequently NBS, aSPU and aSPUw tests are recommended to test for group differences in functional connectivity.

1. INTRODUCTION

Brain functional connectivity has been studied by analyzing time series correlations in regional brain activities. Neurophysiological brain activities are measured by blood oxygenation level dependent (BOLD) signals from resting-state functional magnetic resonance imaging (rs-fMRI) (Lindquist 2008; Smith 2011). Functional brain connectivity can be depicted as a network or graph (Bullmore and Sporns 2009; Habeck and Moeller 2011; He and Evans 2010), which is defined as a set of nodes (or vertices) linked by connections or edges. Nodes represent brain regions and a connection is attached with a weight reflecting the strength of functional correlation between two regions (Varoquaux and Craddock 2013). Most of existing work focuses on estimation of such a network for one subject or a group of subjects (e.g. Cribben et al 2012; Honey et al 2007; Huang et al 2010; Smith 2011; Zhou et al 2006). A key but inadequately addressed question is how to test for possible differences of the brain functional networks between two or more subject groups, say between healthy controls and patients.

Group-level comparison of functional connectivity may shed light on underlying biological processes or disease mechanisms (Smith et al 2012). To study differences between groups of individuals, either individual connections or summary network measures have been used. When performing such group comparisons based on individual connections, a large number of univariate tests are routinely undertaken, and a multiple testing correction, e.g. based on Bonferroni’s method to control the family-wise error rate (FWER) or other methods to control FWER or false discovery rate (FDR), is necessary, which would greatly reduce the statistical power due to the large number of comparisons. At the same time, it is possible that the differences of individual connections are weak, though their aggregated differences can be strong. In such a case, mass-univariate testing, by focusing on the connection with the maximal difference, is often low-powered. On the other hand, global network measures can characterize systematic properties of brain networks (Rubinov and Sporns 2010) and comparisons of one or few global network measures between healthy controls and patients have been conducted to demonstrate connectivity abnormalities in neurological and psychiatric disorders. For example, Wozniak et al (2013) have revealed significantly altered network connectivities in children with fetal alcohol spectrum disorder (FASD) based on the network measures of characteristic path and global efficiency. Yet some network measures have robustness problems (Fornito et al 2010); some anatomical network measures are not straightforward to interpret in the brain functional aspect (Honey et al 2009); and more importantly, there is always the question of which global network measure or measures to use, since the results will largely depend on such a choice. No matter which one to use, as a summary statistic, any global network measure may ignore information about the complex brain system, since each single measure is defined to represent only one aspect of a complex brain network.

As a middle ground between the above two extremes, a global test can be applied to assess significance of overall network differences by summarizing individual connection differences. Network Based Statistic (NBS) is such an omnibus test developed specifically for neuroimaging research to detect network differences (Zalesky et al 2010). NBS controls the FWER by considering an appropriate global statistic measuring the clustering structure of changed edges based on mass-univariate statistics, each performed at every connection comprising the graph, though the global statistic depends on an input parameter to be specified. Since only one single global test is conducted, the issue of multiple comparisons does not arise. However, other than NBS, not many other statistical tests are known or widely used in functional network comparisons. Here, we review and compare the performance of several state-of-the-art statistical tests originally proposed for genetics, ecology and high-dimensional data, in addition to NBS that is familiar to neuroimaging researchers. Specifically, we examine Multivariate Matrix Distance Regression (MDMR) (McArdle and Anderson 2001; Zapala and Schork 2006, 2012), an adaptive sum of powered score (aSPU) test and its weighted version (aSPUw) (Pan et al 2014), and Direction-Projection-Permutation (Wei et al 2014). All of them are omnibus tests assessing global significance of differences across multiple or all edges of the networks to be compared. These methods require only minimal assumptions for validity and use resampling techniques to deal with high dimensional data, whose number of parameters is often much larger than the sample size, for which some classic multivariate tests like MANOVA are not applicable. In particular, to our knowledge, it is the first time that the aSPU/aSPUw tests (Pan et al 2014) and Direction-Projection-Permutation (Wei et al 2014) are applied to high-dimensional rs-fMRI data in this paper. We applied the methods to the FASD data introduced in Wozniak et al (2013) and conducted an extensive simulation study based on the FASD data. The simulation study confirmed the superior performance of NBS, though none of the tests could be a uniform winner across all the situations. For example, in some scenarios, the aSPU and aSPUw tests were more powerful than NBS. Overall, NBS, aSPU and aSPUw tests were the winners and are thus recommended.

The paper is organized as follows. After reviewing basic notation and definitions, we discuss several statistical approaches for testing group differences in brain functional networks. In the following section, we apply the described methods to the FASD data to examine brain functional connectivity differences between a group of children with FASD and a control sample. In Section 4, we use simulations with realistic set-ups mimicking the FASD data to compare the statistical methods for their Type I error rates and power. Discussions of related work are given in Section 5.

2. METHODS

2.1 Data and Notation

Suppose we have N distinct brain regions of interests (ROIs), which define the nodes of the associated networks or graphs. At each node, brain activity is measured in BOLD time series using rs-fMRI (or task-specific fMRI). Given a set of graph nodes, brain connectivity is measured between every pair of N nodes through pairwise correlations of their brain activities; Pearson’s correlations are commonly used. Each pairwise correlation is used as a weight on the edge (or sometimes simply called connection) between the two connected nodes. In this situation, a total of k = N × (N − 1)/2 unique pairwise correlations are estimated, since each node is connected with every other node.

We focus on the case-control study design with possible covariates. To be explicit on the data structure, suppose there are n unrelated subjects, either affected or unaffected by a disorder. We denote a group indicator Y_i = 0 for controls, Y_i = 1 for cases, and covariates for subject i are Z_i = (Z_i1, …, Z_il)′. Denote X_i = (X_i1, …, X_ik)′ a group of unique pairwise correlations, such as k functional brain connections from the i^th subject. Using matrix notation, we denote Y_n×1 a vector for group indicators, X_n×k a matrix of pairwise correlations between nodes, and Z_n×l a covariate matrix. As usual Fisher’s z-transformation is applied to the Pearson correlations to normalize the local correlation measures (Zalesky et al 2010).

2.2 Mass-Univariate Testing

To detect whether there is any difference between functional networks for cases and controls, we might want to test on each individual connection separately. Hence a large number of univariate tests are undertaken, and a multiple testing correction (e.g. based on Bonferroni’s procedure or FDR control) is applied. The often use of a conservative multiple testing correction procedure greatly reduces the power of the comparisons. In addition, we might have a situation where individual connections have only small differences, though their aggregated difference is significant. In such a case, mass-univariate testing is low powered. Either a t-test or marginal logistic regression can be used as the univariate test; the two are asymptotically equivalent. Instead of the Bonferroni correction, we use a resampling-based method to yield an almost exact adjustment for multiple testing, as implemented in the so-called UminP test in genetics.

2.3 Testing Based on Global Network Measures

A small number of neurobiologically meaningful global network measures are often used to quantify some overall features of brain networks. Rubinov and Sporns (2010) reviewed many global network measures that detect functional integration and segregation, quantify centrality of individual brain regions or pathways, characterize patterns of local anatomical circuitry, and test resilience of networks to insult. It is straightforward to compare these global network measures between clinical patients and controls, e.g. to demonstrate connectivity abnormalities in neurological and psychiatric disorders. Each metric is easily computable with some positive normalized weights w_ij (i.e. 0 ≤ w_ij ≤ 1) for any edge connecting nodes i and j, or with a binary measure (often obrained by thresholding w_ij) denoting the presence or absence of the connection. For example, Wozniak et al (2013) computed four global measures for cortical network connectivity to compare the FASD patient group with the controls (i.e characteristic path length, global efficiency, local efficiency, and mean clustering coefficient), finding that the characteristic path length and global efficiency showed significant differences between the two groups.

For illustration, we review four commonly used and representative global network measures. Characteristic path length and global efficiency attempt to measure functional integration in the brain, which would relate to the ability to combine specialized information. Paths connect distinct nodes and edges, representing routes of information flow between pairs of brain regions. Shorter paths imply stronger integration. The average shortest path length between all pairs of nodes in the network is known as the characteristic path length (Watts and Strogatz 1998). The global efficiency is defined as the average inverse shortest path length (Latora and Marchiori 2011). When two nodes are disconnected, the path is defined to have an infinite length and efficiency zero. A binary path length is equal to the number of edges in the path; a weighted path length is equal to the total sum of individual connection lengths which are inversely related to connection weights.

Local efficiency and clustering coefficient aim to measure functional segregation in the brain, quantifying the features of clusters within the network. The presence of clusters in networks suggests that segregated neural processes depend on each other. Connected three nodes form a triangle and segregation measures are based on the number of these triangles in the network. Locally, the fraction of triangles around an individual node is known as the clustering coefficient (Watts and Strogatz 1998). Local efficiency is defined as the averaged efficiency of each node. Latora and Marchiori (2011) suggested that the local efficiency of each node i measures how efficiently information flows between the first neighbors of the node i, when i is removed. The weighted local efficiency is broadly proportional to the weighted clustering coefficient (Onnela 2005). More details on network measures are defined in Rubinov and Sporns (2010).

To test for significant differences in a global network measure without covariates, we can simply use the two-sample t-test for equal means of the network measure between two groups. For example, once all pairwise correlations are measured, we compute a characteristic path length for each subject; each subject is classified into one of two groups, say affected and unaffected; then we would perform the two-sample t-test with the characteristic path length measure of each subject. To incorporate covariates, a logistic regression model can be used with each network measure and covariates as predictors while a group indicator (i.e. disease status) as a binary response variable. For the FASD data analysis and the simulation study, we used logistic regression to identify the network differences between two groups.

Open source Matlab toolbox BCT provides functions to calculate global network measures at http://www.brain-connectivity-toolbox.net.

2.4 Network Based Statistic

Network Based Statistic (NBS) is a method that takes advantage of the clustering structure of network differences: the edges with different weights across the groups often form a connected component or subnetwork, i.e. a cluster. In these situations, NBS potentially yields greater power than other methods that ignore such a clustering structure.

NBS works as follows (Zalesky et al 2010). Suppose we have n subjects and k edges in each subject’s network. For each edge j = 1, … k, a generalized linear model is separately fitted to each connection to compute a contrast statistic. For our concrete situation of two group comparison with covariates Z, we can consider two indicator variables, G₁ and G₂, denoting G_1i = 1 and G_2i = 0 if subject i is a control; G_1i = 0 and G_2i = 1 otherwise. The j^th connection is modeled as

$$X_{ij}=G_{1i}{a}_1+G_{2i}{a}_2+\sum _{m=1}^l{Z}_{im}{\delta }_m+{\mathrm{e}}_{ij}i=1,\dots ,n.$$

where the errors e_ij are independent and identically distributed as Gaussian N(0, σ²). We can formulate contrasts to compare a₁ and a₂ at each edge separately to test the hypothesis that the edges between the two groups come from two distributions with equal means with H₀: a₁ = a₂, which can be described as c′a = 0 with $\mathbf{c}={[\begin{array}{ccc}1& -1& \mathbf{0}\end{array}]}^{\prime }$ and $\mathbf{a}={[\begin{array}{ccccc}{a}_1& a_2& {\delta }_{i1}& \dots & {\delta }_{il}\end{array}]}^{\prime }$.

Denote G₁ = (G₁₁, …, G_1n)′ and G₂ = (G₂₁, …, G_2n)′ as n × 1 vectors, $\mathbf{D}=[\begin{array}{ccc}{\mathbf{G}}_{\mathbf{1}}& {\mathbf{G}}_{\mathbf{2}}& \mathbf{Z}\end{array}]$ , and X_j = Da+e. The contrast for the j^th connection, can be tested with the following test statistic

$$T_j=\frac{{\mathbf{c}}^{\prime }\mathbf{a}}{\sqrt{{\sigma }^2·{\mathbf{c}}^{\prime }{({\mathbf{D}}^{\prime }\mathbf{D})}^{-\mathbf{1}}\mathbf{c}}}.$$

Supra-thresholded connectivity represents edges each with a test statistic T_j that exceeds a predetermined threshold. A cluster is defined as a connected component composed of supra-thresholded edges. NBS identifies the maximum size (i.e. number of edges) of supra-thresholded connectivity s, and detects a significant subnetwork (or cluster) differentiating two groups. To make inference, permutation is used (Nichols and Holmes 2001). For each permutation b = 1, … B, members of the two samples are randomly permuted and the size of the largest identified cluster s^(b) is calculated. This yields an empirical null distribution of maximal suprathreshold cluster size. Then a p-value of testing for group differences is calculated using this null distribution: $\mathrm{p}-\text{value}={\sum }_{b=1}^{B}I(s^{(b)}\ge s)/B$.

For ease of notation, we use nbs(t) as a predetermined threshold that is the t^th percentile in absolute values of T_j’s; that is, t is the proportion of T_j’s satisfying |T_j | ≤ nbs(t).

NBS assumes that the edges associated with the contrast of interest are not isolated from each other and thus form a cluster. In general, suprathreshold-cluster-tests are more powerful for functional neuroimaging data than edge-based-threshold tests like the mass-univariate testing. However, the power of NBS test depends on the specified threshold parameter (Zalesky et al 2010). With a low threshold, large-scale networks composed of many suprathresholds are to be expected, so intense and small-sized subnetworks will be undetected. At higher thresholds, these small subnetworks will be detected, but lower intensity clusters may go undetected below the threshold. Hence it is a drawback of NBS for its dependence on the specified threshold parameter t while it is often unknown which t to use in practice. An appealing aspect of NBS is that it provides the topological clusters among the set of the suprathresholded edges as an evidence against the null hypothesis, which allows to visualize significant subnetworks.

Matlab Network Based Statistic toolbox is an open source implementing NBS approach at https://sites.google.com/site/bctnet/comparison/nbs

2.5 Multivariate Matrix Distance Regression

MDMR is a nonparametric modification to MANOVA, avoiding the latter’s assumption of multivariate normal responses (McArdle and Anderson 2001). For simplicity, we first consider the situation without covariates. As MANOVA, MDMR is based on the following multivariate regression model:

$$E(X_i)=b_0+Y_i{b}_1.$$

The key interest is to test H₀: b₁ = 0 versus H₁: b₁ ≠ 0. In addition to the normality assumption on X_i, MANOVA requires that the sample size n > k, which is not the case here with high-dimensional fMRI data. As an alternative, MDMR performs as follows.

• Step 1. Calculate an n × n distance matrix for all pairs of subjects by D = (D_ij) with D_ij = d(X_i, X_j) and d() being a distance or semi-distance metric.

• Step 2. Calculate $A=(-D_{ij}^2)$.

• Step 3. Obtain a centered similarity matrix G = (I − 11′/n)A(I − 11′/n), where 1 is an n by 1 vector of all 1’s.

• Step 4. Denote Y_n×1 as the vector of group indicators. Calculate the projection matrix H = Y (Y′ Y)⁻¹Y ′.

• Step 5. Calculate a pseudo F-statistic as

  $$F=\frac{tr(\mathit{HGH})}{tr[(I-H)G(I-H)]},$$ (1)

  where tr(A) is the trace of matrix A.

The equation (1) is analogous to Fisher’s F statistic for MANOVA when the Euclidean distance d() is used. McArdle and Anderson (2001) suggested that any multivariate distance measure like Bray and Curtis (1957) can be used and permutation is used to get the p-value. For each permutation b = 1, …, B, two group memberships are randomly permuted to generate Y^b and compute F^(b), the value of test statistic F based on the new data set {Y^b, X}. The p-value can be obtained as ${\sum }_{b=1}^{B}I(F^{(b)}\ge F)/B$.

In multifactorial designs, an appropriate pseudo F statistic can be constructed to incorporate covariates (McArdle and Anderson 2001; Reiss et al 2010). MDMR has been applied to genetics (Wessel and Schork 2006) and more recently to brain connectivity analysis (Reiss et al 2010; Shehzad et al 2014); while the application of Reiss et al (2010) was similar to ours in testing all ROIs’ connections simultaneously, Shehzad et al (2014) considered each ROI separately for its connections to other ROIs.

In our analyses, we used the Euclidean distance metric d(). MDMR is implemented in R package vegan.

2.6 The SPU and aSPU Tests

Pan et al (2014) proposed a family of association tests, the sum of powered score (SPU) tests, aiming to yield at least one powerful test for a given situation. The SPU tests were developed for conducting global testing for association between a response variable and multiple genetic variants. Each SPU test is based on the score vector from a general regression model, hence can be applied to various types of the response variable with or without covariates. Consider a logistic regression model with k functional connections and l covariates:

$$\text{Logit}[Pr(Y_i=1)]={\beta }_0+\sum _{j=1}^k{X}_{ij}{\beta }_j+\sum _{m=1}^l{Z}_{im}{\delta }_m.$$ (2)

The null hypothesis to be tested is H₀ : β = (β₁, …, β_k)′ = 0. Under H₀, there is no group difference in functional brain connectivity, and the model reduces to

$$\text{Logit}[Pr(Y_i=1)]={\beta }_0+\sum _{m=1}^l{Z}_{im}{\delta }_m.$$ (3)

Fitting the above null model (3), which is often much lower-dimensional as compared to the full model (2), one obtains the maximum likelihood estimates β̂₀ and δ̂_m’s, and thus ${\widehat{Y}}_i=1/[1+exp(-{\widehat{\beta }}_0-{\sum }_{m=1}^l{Z}_{im}{\widehat{\delta }}_m)]$. The score vector U = (U₁, …, U_k)′ for β in model (2) is

$$U=\sum _{i=1}^n{X}_i(Y_i-{\widehat{Y}}_i).$$

Each score component U_j contains information on the significance of each β_j, i.e. non-zero effects of each connection. Intuitively, each U_j can be regarded as measuring the correlation between the jth connection X_ij and the residuals (resulting from ignoring the connection); if the connection is indeed related to the response, then it is expected that the connection X_ij and the residuals Y_i − Ŷ_i will be related. In fact, this is exactly the idea of diagnostic model checking in examining a residual plot for an omitted predictor to see whether the omitted predictor is needed in a regression model. Each SPU test can be depicted as combining a collection of univariate tests, each on a connection of the network. Specifically, given γ ≥ 1, the SPU(γ) test statistic is defined as

$$T_{\mathit{SPU}(\gamma )}=\sum _{j=1}^k{\zeta }_j{U}_j=\sum _{j=1}^k{U}_j^{\gamma },$$

where ${\zeta }_j=U_j^{\gamma -1}$ can be regarded as a weight for the j^th component of U. With various values of γ ≥ 1, one of the SPU(γ) tests may maintain high power for a given situation. As γ increases, the SPU(γ) test puts more weights on the fewer and larger components of U. Eventually, as γ → ∞, it only takes the maximum component of the score vector and the test statistic is defined as $T_{\mathit{SPU}(\infty )}={max}_{j=1}^k\mid U_j\mid$.

To make statistical inference for a circumstance where the number of parameter k is large compared to the sample size n, Pan et al (2014) proposed using the parametric bootstrap (with covariates) or permutation (without covariates) to relax the asymptotic normality assumption on the score vector U: First, we fit a null model under H₀ by regressing Y_i on the covariates Z_i to obtain fitted values Ŷ = (Ŷ₁, …, Ŷ_n)′, then simulate new responses $Y^{(b)}={(Y_1^{(b)},\dots ,Y_n^{(b)})}^{\prime }$ with $Y_i^{(b)}~\text{Bin}(1,{\widehat{Y}}_i)$ independently for b = 1, …, B. The test statistic $T_{\mathit{SPU}}^{(b)}$ is calculated based on simulated data {Y^(b), X, Z}. Finally we compute the $\mathrm{p}-\text{value}={\sum }_{b=1}^B[I(\mid T_{\mathit{SPU}}^{(b)}\mid \ge \mid T_{\mathit{SPU}}\mid )+1]/(B+1)$ . For a case without covariates, the permutation method can be used.

It is interesting to note that the family of the SPU tests cover several existing tests as special cases. The SPU(1) test is equivalent to the Sum test, a burden test used in genetic rare variant analysis (Pan 2009), and similar to that used in fMRI data for network testing (Meskaldji et al 2011), in which the weights of all the edges are aggregated under the working assumption that the edge weights are all changed with the same magnitude and direction between the two groups. The SPU(1) test retains high power if all or most of the edge weights of the networks for the two groups differ in one direction, each with a small magnitude. However, the SPU(1) test may lose power when both positive and negative differences across the edges exist, and/or there are only few edges with changes. On the other hand, the SPU(2) test is more powerful under these situations (i.e. in the presence of edge changes in both directions and/or few edge changes). As shown in Pan (2011), since the SPU(2) test is exactly the same as the sum of squared score (SSU) test, it is closely related to MDMR (McArdle and Anderson 2001) and kernel machine regression (KMR) (Liu et al 2007; Ge et al 2012). The SPU(∞) test share the same spirit of mass-univariate testing in that only the most significant component or edge is taken as the evidence against the H₀. They may differ in how to adjust for multiple testing; the SPU(∞) test employs a resampling technique to have an almost “exact” adjustment.

Since the power of a SPU(γ) test depends on the choice of γ while the optimal γ depends on the unknown true association pattern, Pan et al (2014) proposed an adaptive SPU (aSPU) test that data-adaptively chooses an optimal value of γ from a set of supplied candidate values of γ, say Γ. Suppose that the p-value of the SPU(γ) test is P_SPU(γ), then the aSPU test’s combining procedure takes the minimum p-value:

$$T_{\mathit{aSPU}}=\underset{\gamma \in \mathrm{\Gamma }}{min}{P}_{\mathit{SPU}(\gamma )}.$$

Here, T_aSPU is not a genuine p-value; we use the permutation or parametric bootstrap to estimate its p-value. It is interesting to note that, with the same set of the resamples, the p-values of all the SPU and aSPU tests can be simultaneously calculated. Specifically, once resample Y^(b) is generated and the corresponding score vector U^(b) is obtained for b = 1, 2, …, B, we calculate each SPU test statistic $T_{\mathit{SPU}(\gamma )}^{(b)}$ and its corresponding p-value $p_{\gamma }^{(b)}={\sum }_{b_1\ne b}[I(T_{\mathit{SPU}(\gamma )}^{(b_1)}\ge T_{\mathit{SPU}(\gamma )}^{(b)})+1]/B$ , for b = 1, …, B; then calculate the aSPU test statistic, $T_{\mathit{aSPU}}^{(b)}={min}_{\gamma \in \mathrm{\Gamma }}{p}_{\gamma }^{(b)}$. The final p-value of the aSPU test is $P_{\mathit{aSPU}}={\sum }_{b=1}^B[I(T_{\mathit{aSPU}}^{(b)}\le T_{\mathit{aSPU}})+1]/(B+1)$.

As discussed in Pan et al (2014), the following considerations guide the choice of the integers γ ≥ 1 in Γ. First, we would include γ = 1 and γ = 2 in Γ to cover the Sum and SSU tests. Note that the SSU test is equivalent to MDMR if the Euclidean distance is used in the latter as usual (Pan 2011). Second, depending on whether the individual connectivity association directions vary or not between the groups, we may need to use either even or odd integers γ’s to yield high power. Third, depending on how many individual connection strengths are expected to be different between the two groups, we may use smaller or larger γ’s. In general, if there is a smaller fraction of the true connection changes, then a larger γ is needed. A pratcical rule is to use Γ = {1, 2, …, γ₁, ∞} such that SPU(γ₁) gives the result close to that of SPU(∞). In this paper, for simplicity, we used Γ = {1, 2, …, 8, ∞}.

The aSPU test can be used for variable selection (Pan et al 2014). Suppose that the aSPU test selects γ̂ = arg min_γ∈Γ∞ P_SPU(γ). The individual connections can be ordered based on their contributions to the score statistics: the larger is connection j’s score statistic |U_j |, the more significant is the connection j. In this way, we can order the connections by the corresponding |U_j |’s. Alternatively, we can select the top 1 ≤ k₁ ≤ k connections such that their accumulative contribution ${\sum }_{j=1}^{k_1}{\mid U_j\mid }^{\widehat{\gamma }}/{\sum }_{j=1}^k{\mid U_j\mid }^{\widehat{\gamma }}\ge {\alpha }_1$ for a specified threshold 0 < α < 1.

R code for the SPU and aSPU tests is provided by Pan et al (2014) and will be posted on our web site.

2.7 The SPUw and aSPUw Tests

We follow the outline in Pan et al (2014) to construct a inverse-variance weighted version of the SPU and aSPU tests, called the SPUw tests and aSPUw test respectively. The SPU and aSPU tests ignore possibly different variabilities across the score components, while the SPUw and aSPUw tests incorporate the variances as weights η_j. The test statistic of SPUw(γ) test is computed as

$$T_{\mathit{SPUw}(\gamma )}=\sum _{j=1}^k{\eta }_j{U}_j^{\gamma }=\sum _{j=1}^k{(U_j/\sqrt{V_{jj}})}^{\gamma },$$

where V_jj is a diagonal element of

$$V=\widehat{\mathit{Cov}}(U\mid H_0)=\sum _{i=1}^n{(Y_i-{\widehat{Y}}_i)}^2(X_i-\overline{X}){(X_i-\overline{X})}^{\prime },$$

the estimated covariance matrix of the score vector under H₀ with $\overline{X}={\sum }_{i=1}^n{X}_i/n$. The aSPUw test combines the p-values of the SPUw tests:

$$T_{\mathit{aSPUw}}=\underset{\gamma \in \mathrm{\Gamma }}{min}{P}_{\mathit{SPUw}(\gamma )}.$$

Using the parametric bootstrap or permutation method described earlier, we can obtain p-values for the SPUw tests and aSPUw test simultaneously for any given Γ; the choice of Γ is similar to that for the aSPU test.

Similar to SPU(∞), the SPUw(∞) test is exactly a mass-univariate testing procedure in considering only the most significant component among multiple (score) test statistics; it is a maximum statistic as discussed by Nichols and Holmes (2002). The aSPUw test is also useful in variable selection in the same way as the aSPU test, by ordering the connections by the magnitudes of their corresponding score statistic components.

We implemented the SPUw and aSPUw tests in R; the code will be posted on our web site.

2.8 Direction-Projection-Permutation

Direction-Projection-Permutation (DiProPerm) is a non-parametric procedure that can be used to test for equal distributions or equal means between two groups of high dimensional data (Wei et al 2014). Binary classification is to separate a dataset into two groups based on observed input vectors in ℝ^k, constructing a hyperplane. DiProPerm relies on the binary linear classifier which achieves high classification accuracy on the training data in high dimensional low sample sized settings.

To be explicit, DiProPerm assesses any difference in the distribution of k dimensional brain connectivity between control and case groups. Let X₀₁, mldr;, X_0m and X₁₁, …, X_1nbe independent random samples of k dimensional brain connectivity from multivariate distribution F₀ and F₁ respectively (i.e. F₀ for controls and F₁ for cases). Here each sample X_j is a k by 1 vector. The null hypothesis of interest is that cases and controls have the same distribution (i.e. H₀ : F₀ = F₁) and an alternative is H_α : F₀ ≠ F₁. Wei et al (2014) proposed DiProPerm as a three-step procedure: direction, projection and permutation.

The direction step of DiProPerm is to construct a hyperplane for binary classification on the two groups and to find the normal vector to the separating hyperplane. For the classifiers, the Distance Weighted Discrimination (DWD) or the Support Vector Machine (SVM) could be considered (Marron et al 2007; Hastie et al 2001). The second step is to project data onto the normal vector and to calculate a univariate statistic such as a two-sample t-statistic or mean differences. We used sample mean differences for the statistic for the FASD data analysis and the simulation study. The final step of DiProPerm is to use permutation to assess the significance of the test statistic. Since DiProPerm test cannot incorporate covariates terms, it was only applied to the models without considering covariate effects.

Software for the DiProPerm procedure is available at http://www.unc.edu/~marron/marron_software.html

2.9 Comparison of the Methods

It is noted that many of the methods are related. First, some of the global tests such as NBS, SPU and SPUw tests are all related to mass-univariate testing. These global methods can be regarded as various ways of combining the univariate test statistics. For example, each score component U_j can be regarded as a summary statistic for testing for association between the group indicator Y_i and an individual network connection X_ij. In fact, as mentioned earlier, the SPUw(∞) test is exactly a mass-univariate testing procedure using a resampling method (e.g. permutation or bootstrap) for multiple testing adjustment, which is almost exact and more accurate than the more conservative Bonferroni method.

Second, for univariate testing, some methods, such as the SPU and SPUw tests, are based on regressing Y_i on each X_ij, while others, such as NBS and MDMR, are based on regressing X_ij on Y_i. These two ways of testing for association between Y_i and X_ij are (asymptotically) equivalent. For simplicity, let us consider the case without covariates. The two regression models are

$$\text{Logit}[E(Y_i))]={\beta }_0+X_{ij}{\beta }_j,E(X_{ij})={\alpha }_0+Y_i{\alpha }_j,$$

for a fixed j and i = 1, …, n. The corresponding two null hypotheses are H₀: β_j = 0 and $H_0^{\prime }:{\alpha }_j=0$. Since both models are generalized linear models (GLMs) with a canonical link function (McCullagh and Nelder 1983), it is easy to verify that their score functions for β_j and α_j under H₀ and $H_0^{\prime }$ respectively are both equal to

$$\sum _{i=1}^n(X_{ij}-{\overline{X}}_{.j})(Y_i-\overline{Y})$$

with ${\overline{X}}_{.j}={\sum }_{i=1}^n{X}_{ij}/n$ and $\overline{Y}={\sum }_{i=1}^n{Y}_i/n$. Hence their score tests will be exactly the same, which will also be asymptotically equivalent to the Wald and likelihood ratio tests. In particular, the t-test used in univariate testing or NBS is asymptotically equivalent to the above score test based on either model. This connection goes beyond univariate testing; there is also an equivalence between regressing Y_i on X_i = (X_i1, …, X_ik)′, as used in the SPU tests and KMR, and regressing X_i on Y_i as in MDMR: if the Euclidean distance d() is used in MDMR and if a linear kernel is used in KMR, then MDMR, KMR and the SSU (i.e. SPU(2)) test are all equivalent (Pan 2011). This issue is also discussed in the framework of GEE (Zhang et al 2014).

There is an asymptotically consistent and permutation-based test for high-dimensional data (Szekely and Rizzo 2004), which gave results very similar to that of MDMR in our numerical results (not shown). Hua and Ghosh (2014) pointed out its equivalence to KMR; by the close connections among MDMR, KMR and the SPU(2) (i.e. SSU) test, we obtain its equivalence to other tests.

As Pan et al (2014) pointed out, the SPU test (and SPUw test) can be extended to other generalized linear models. Specifically, let a linear predictor be ${\eta }_i={\beta }_0+{\sum }_{j=1}^k{X}_{ij}{\beta }_j+{\sum }_{m=1}^l{Z}_{im}{\delta }_m$, and a link function g(·) links the mean of the response variable, μ_i = E(Y_i), and the linear predictor: $g({\mu }_i)={\eta }_i={\beta }_0+{\sum }_{j=1}^k{X}_{ij}{\beta }_j+{\sum }_{m=1}^l{Z}_{im}{\delta }_m$. Then the j^th component of the score vector and its variance are (Agresti 1990, p.448–449):

$$\begin{array}{l}{U}_j=\sum _{i=1}^b\frac{(Y_i-{\mu }_i)X_{ij}}{var(Y_i)}\frac{\partial {\mu }_i}{\partial {\eta }_i},\\ var(U_j)=\sum _{i=1}^n\frac{X_{ij}^2}{var(Y_i)}{(\frac{\partial {\mu }_i}{\partial {\eta }_i})}^2,\end{array}$$

for j = 1, ···, k. For example, we can use a probit model, instead of the logit model, to test for group differences in brain connectivity. The probit model employs a probit link function g() = Φ⁻¹(), where Φ() is the cumulative distribution function of the standard normal distribution. Under the null hypothesis (i.e. β = (β₁, …, β_k)′= 0), the score vector of the probit model is

$$U=\sum _{i=1}^n\frac{\varphi ({\widehat{\beta }}_0+{\sum }_{m=1}^l{Z}_{im}{\widehat{\delta }}_m)}{{\widehat{Y}}_i(1-{\widehat{Y}}_i)}·X_i(Y_i-{\widehat{Y}}_i),$$

where β̂₀ and δ̂_m are MLE under the null model; ${\widehat{Y}}_i=\mathrm{\Phi }({\widehat{\beta }}_0+{\sum }_{m=1}^l{Z}_{im}{\widehat{\delta }}_m)$; and ϕ() is the probability density function of the standard normal distribution. Compared to the score vector measuring the correlations between each connection and the residuals in the logit model, the score vector here is based on a weighted correlation between each connection and the residuals from the null model. Then we can plug-in the score vector into the SPU and aSPU tests as before. Similarly, the SPU and aSPU tests can be applied to other regression models for continuous or count response data.

3. APPLICATION TO FASD DATA

3.1 MRI Acquisition and Processing

We used the FASD data of Wozniak et al (2013). For the initial MRI data acquisition, a Siemens 3T TIM Trio MRI scanner with a 12-channel parallel array head coil was used. Scans included a structural T1-weighted scan, a resting-state fMRI scan (TR= 2000ms, TE= 30ms, 34 interleaved slices, no skip, voxel size= 3.45 × 3.45 × 4.0mm, FOV = 220mm, flip angle = 77 degrees, 180 measures.), and a field map; Additional details are in included in Wozniak et al. (2013). During the resting-state scan, participants were instructed to close their eyes and remain still.

The fMRI data were processed with modified “1000 Functional Connectome (TFC)” preprocessing scripts (www.nitrc.org/plugins/mwiki/index.php/fcon_1000). Tools from AFNI (Cox, 1996) and the FMRIB Software Library (FSL) version 4.1.6 (Smith et al., 2004; Woolrich et al., 2009) were used in the TFC processing. This included skull stripping, motion correction, geometric distortion correction using FSL’s FUGUE (added to the TFC pipeline), spatial smoothing (FWHM of 6 mm), grand mean scaling, band pass temporal filtering (0.005 to 0.1 Hz), and quadratic de-trending. The TFC processing of the T1 volume included skull stripping and FSLs FAST tissue segmentation to define whole brain, white matter and ventricular cerebrospinal fluid (CSF) regions of interest (ROIs). The skull-stripped T1 and tissue segmentation ROIs were registered to the fMRI data using FSL’s FLIRT. Time courses from the three tissue segmentation ROIs, along with the six motion parameters, were used as voxel-wise nuisance regressors in the TFC processing of the fMRI data. Cortical parcellation of the T1 volume in 34 ROIs was done with FreeSurfer version 4.5 (surfer.nmr.mgh.harvard.edu) (Dale et al. 1999). Data was visually inspected, but hand-editing was not employed. As this paper is focused on comparing statistical methodologies, we did not manually edit the Freesurfer segments; however, in actual patient or cognitive studies, manual edits are necessary.

The 68 FreeSurfer cortical parcellations along with 12 sub-cortical regions were registered to the TFC-processed fMRI data using FreeSurfer’s bbregister (Greve and Fischl, 2009). The parcellations were dilated during registration but none were allowed to overlap and voxels outside the TFC brain-mask were excluded. ROIs that contained fewer than 10 fMRI voxels for any subject were excluded from the final analysis. This resulted in the exclusion of 6 cortical ROIs (bilateral entorhinal, frontal pole and temporal pole), leaving a total of 62 cortical ROIs (31 per hemisphere). The mean fMRI time-series of all voxels within each ROI were then extracted and used for each subject.

3.2 Data Analysis

Wozniak et al (2013) compared functional network connectivities in 24 FASD patients, aged 10 to 17, with 31 matched controls using resting-state fMRI. They compared four global network measures of cortical network connectivity between FASD patients and controls: characteristic path length, mean clustering coefficient, local efficiency, and global efficiency. N = 62 cortical ROIs were considered. The resting-state fMRI signals for each region were measured at 180 time points. For our analyses, N = 74 ROIs including 12 sub-cortical regions were considered. Fisher’s z-transformation was applied to the Pearson correlations between all pairs of N = 74 ROIs for k = 2701 edges.

Table 1 contains the p-values from the discussed methods for testing differences in brain functional networks between the two groups. The tests showing significant p-values (< 0.05) are SPU(1), aSPU, SPUw(1), SPUw(3), aSPUw and NBS. These results are consistent with Wozniak et al (2013), revealing altered network connectivity in children with FASD. To specify a predetermined threshold for NBS analysis, nbs(0.1), nbs(0.25), nbs(0.5) and nbs(0.75) (i.e. the 10^th, 25^th, 50^th and 75^th percentiles of the absolute values of T_j statistics) were arbitrarily chosen, since we had no prior knowledge on which threshold would give highest power. We also applied the SPU and aSPU tests based on the probit model (instead of the default logit model), and obtained significant p-values, 0.013 and 0.045 for SPU(1) and aSPU respectively, which were similar to the results based on the logit model shown in Table 1. The p-values from the SPU/aSPU tests, SPUw/aSPUw tests and MDMR were based on 1000 permutations (or bootstrap samples with covariates); NBS based on 5000.

Table 1.

P-values for network comparison without any covariates in the FASD data.

Test	SPU(1)	SPU(2)	SPU(3)	SPU(4)	SPU(5)	SPU(6)	SPU(7)	SPU(8)	SPU(∞)	aSPU
P-value	0.009	0.324	0.090	0.359	0.275	0.408	0.465	0.486	0.672	0.032
Test	SPUw(1)	SPUw(2)	SPUw(3)	SPUw(4)	SPUw(5)	SPUw(6)	SPUw(7)	SPUw(8)	SPUw(∞)	aSPUw
P-value	0.005	0.270	0.019	0.302	0.057	0.340	0.117	0.378	0.590	0.021
Test	MDMR	DiProPerm	nbs(0.1)	nbs(0.25)	nbs(0.5)	nbs(0.75)	CharPath	Eclust	Eglob	Eloc
P-value	0.332	0.621	0.003	0.007	0.020	0.050	0.759	0.764	0.995	0.828

For mass-univariate analyses, we first used univariate logistic regression with the Bonferroni adjustment. Each edge was fitted as a predictor and the group indicator Y_i was used as a response variable. No individual test survived the corrected significance level of 0.05/2701 (not shown). Furthermore, the permutation-based univariate SPUw(∞) test did not give a significant p-value either

As in Wozniak et al (2013), we computed four global network measures: characteristic path length (CharPath), mean of clustering coefficient (Eclust), local efficiency (Eloc), and global efficiency (Eglob). Network measures were computed based on the magnitudes of Pearson’s correlations; a logistic regression model was used to test the group differences in each network measure. As shown in Table 1, no network measure showed any significant difference between FASD patients and controls, while Wozniak et al (2013) found the significant differences in the characteristic path length and global efficiency. Wozniak et al (2013) included 20% of edges which fully connected all regions to compute each global network measure based on 62 ROIs, but we used all edges from 74 ROIs for a fair comparison with the other methods.

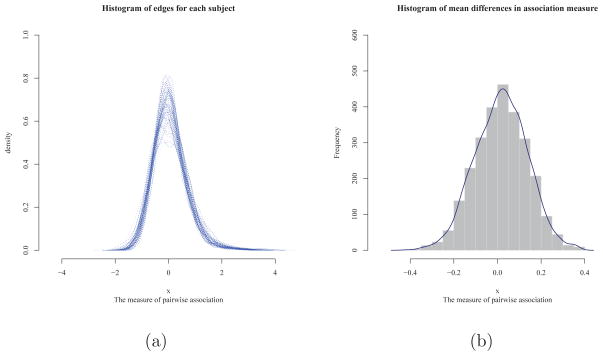
Figure 1(a) illustrates the distribution of z-transformed correlations for 2701 edges. It shows that all 55 subjects had bell-shaped distributions centered around 0 for the correlation measures. The proportion of correlation measures having absolute value less than 1 was about 90%. This implies that mostly weak edges or connections comprised the brain functional networks in the FASD data. These features explain the results in Table 1. As γ increases, the SPU(γ) test puts more weights on the larger components of the score vector, ignoring components of weak edges, leading to less significant p-value. In contrast, the SPU(1) and SPUw(1) tests gave the most significant p-values among the SPU and SPUw tests. This was in agreement with the results of NBS: nbs(0.1) gave the most significant p-value, since at a low threshold, we could include a larger number of weak edges comprising clusters in the FASD data. At higher thresholds, larger p-values were observed. This suggests that at high threshold, few isolated edges were less likely to comprise a large cluster in the FASD data. Zalesky et al (2010) pointed out that, as the size of the cluster decreases, it becomes more difficult to identify group differences with NBS. Note that NBS is utterly powerless in the extreme case when a single isolated connection comprises the cluster.

Figure 1.

Histograms of functional connectivity in the FASD data.

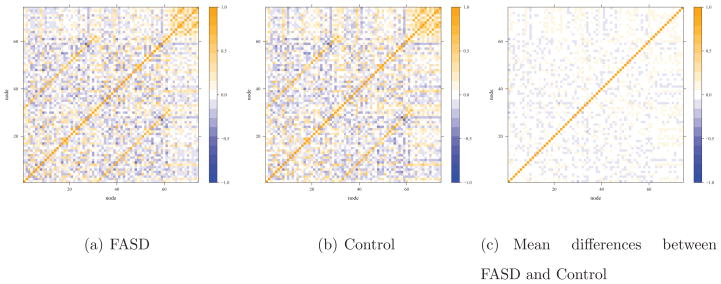
Across the subjects, the minimum measure of correlations was −2.53 and the maximum was 4.41. We obtained mean values of z-transformed correlations for each connection and took their differences between the FASD and control groups. Figure 1(b) shows the histogram of the mean differences in z-transformed correlations for the edges. Among 2701 edges, 1870 edges (70 %) had the mean differences less than 0.1 between the case and control groups. The direction of differences was slightly skewed to the left. Figure 2 illustrates the Pearson correlations structure among the 74 ROIs with warm color representing positive correlations, while cool color for negative correlations. In Figure 2(a) and (b), FASD and control groups show similar features in its functional interactions among 74 ROIs (nodes). Hence, there seemed to be only subtle but extensive differences in the individual network connections between the two groups, explaining why the the SPU(1), aSPU, SPUw(1) and aSPUw tests, and NBS with nbs(0.1) gave significant p-values.

Figure 2.

Heatmaps for functional connectivity in the FASD data.

The original study of Wozniak et al (2013) concentrated on two-sample comparisons using the t-test on several global network measures. The presented methods here are based on a general regression model, hence can deal with covariates. In our data analyses, we also included gender and age as covariates, but reached similar conclusions, presumably due to non-significant covariate effects (Table 2). The p-values from the SPU(1) and aSPU tests based on the probit model were 0.014 and 0.045, almost exactly the same as those without covariates. We also applied a data-normalization procedure called global signal regression (GSReg) (Saad et al 2013) before testing group differences with the various methods, yielding no significant results; the suitability of GSReg is currently still under debate (Saad et al 2013; Shehzad et al 2014).

Table 2.

P-values for network comparison after adjusting for age and gender in the FASD data.

Test	SPU(1)	SPU(2)	SPU(3)	SPU(4)	SPU(5)	SPU(6)	SPU(7)	SPU(8)	SPU(∞)	aSPU
P-value	0.009	0.312	0.085	0.348	0.236	0.391	0.366	0.437	0.759	0.031
Test	SPUw(1)	SPUw(2)	SPUw(3)	SPUw(4)	SPUw(5)	SPUw(6)	SPUw(7)	SPUw(8)	SPUw(∞)	aSPUw
P-value	0.008	0.422	0.028	0.408	0.065	0.411	0.112	0.421	0.447	0.035
Test	MDMR	DiProPerm	nbs(0.1)	nbs(0.25)	nbs(0.5)	nbs(0.75)	CharPath	Eclust	Eglob	Eloc
P-value	0.468	-	0.009	0.017	0.064	0.081	0.673	0.862	0.919	0.925

4. SIMULATION STUDY

4.1 Simulation Design

We used simulations with realistic set-ups mimicking the FASD data to compare the discussed approaches for their Type I error rates and power to detect network connectivity differences between two groups. For the main factors influencing power, we considered general network dissimilarity between two groups, edge-wise network differences between two groups, network sparsity, and thresholding effect.

The degree of network dissimilarity between two groups was controlled by a parameter ω. Suppose μ₀ and μ₁ were respectively sample mean vectors of 2701 edges of the control and case groups in the FASD data, and ${\mathit{\mu }}_0^{\ast }$ and ${\mathit{\mu }}_1^{\ast }$ were parameters to be used for simulating data defined as

$$\begin{array}{c}{\mathit{\mu }}_0^{\ast }={\mathit{\mu }}_0,\\ {\mathit{\mu }}_0^{\ast }-{\mathit{\mu }}_1^{\ast }=\omega ·({\mathit{\mu }}_0-{\mathit{\mu }}_1).\end{array}$$

When ω > 1, the extent of dissimilarity between the two groups (e.g. ${\mathit{\mu }}_0^{\ast }-{\mathit{\mu }}_1^{\ast }$) increased as compared to that of the FASD data, while the dissimilarity decreased when ω < 1.

We defined a parameter τ to determine the proportion of edges from two groups to have the same true mean. In other words, τ determines the edge-wise differences between two mean vectors ${\mathit{\mu }}_0^{\ast }$ and ${\mathit{\mu }}_1^{\ast }$. Denote μ₀ − μ₁ = d. We then defined

$${\mathit{\mu }}_0^{\ast }-{\mathit{\mu }}_1^{\ast }=\omega ·({\mathit{\mu }}_0-{\mathit{\mu }}_1)·[I(\mid \mathit{d}\mid >\mathrm{\tau })],$$

where I is an indicator function operating component-wise, and τ is the τ^th percentile for absolute values of the components of d, {d_j, j = 1, ···, 2701}. That is, when |d_j| ≤ τ, the difference between the j^th component of ${\mathit{\mu }}_0^{\ast }$ and ${\mathit{\mu }}_1^{\ast }$ was defined as 0 (i.e. ${\mu }_{0j}^{\ast }-{\mu }_{1j}^{\ast }\triangleq 0$ ). and ${\mu }_{0j}^{\ast }={\mu }_{1j}^{\ast }={\mu }_{0j}-\omega ·({\mu }_{0j}-{\mu }_{1j})/2$, where μ_0j and μ_1j were the j^th components of sample mean vectors μ₀ and μ₁. Hence, as τ increased, we had more edges unchanged between the two groups.

Some studies have suggested that true brain networks may be sparse (Hilgetag et al 2002). Hence, we generated sparse networks by setting most edges having mean weight 0 when the edges’ weights were not changed between the two groups:

$$\begin{array}{c}{\mathit{\mu }}_0^{\ast }-{\mathit{\mu }}_1^{\ast }=\omega ·({\mathit{\mu }}_0-{\mathit{\mu }}_1)·[I(\mid \mathit{d}\mid >\mathrm{\tau })],\\ {\mu }_{0j}^{\ast }={\mu }_{0j}·I(\mid d_j\mid >\mathrm{\tau }).\end{array}$$

Hence we had ${\mu }_{0j}^{\ast }={\mu }_{1j}^{\ast }=0$ when |d_j| ≤ τ.

There is evidence showing that connectivity changes between two conditions could be in one direction; for example, functional connectivity could be weakened in cases than in controls (Eloyan et al 2012; Mostofsky et al 2008). To mimic this circumstance, we defined

$$\begin{array}{c}{\mathit{\mu }}_0^{\ast }-{\mathit{\mu }}_0,\\ {\mathit{\mu }}_0^{\ast }-{\mathit{\mu }}_1^{\ast }=\omega ·\mid {\mathit{\mu }}_0-{\mathit{\mu }}_1\mid [I(\mid \mathit{d}\mid >\mathrm{\tau })].\end{array}$$

When |d_j| ≤ τ, we defined ${\mu }_{0j}^{\ast }={\mu }_{1j}^{\ast }={\mu }_{0j}-\omega ·\mid {\mu }_{0j}-{\mu }_{1j}\mid /2$. Then we had the edge weights differed in one direction when |d_j| ≤ τ, i.e. ${\mathit{\mu }}_0^{\ast }\ge {\mathit{\mu }}_1^{\ast }$.

In each group, the correlation measures assigned to the edges were randomly sampled from a multivariate Gaussian distribution with mean ${\mathit{\mu }}_0^{\ast }$ for controls (or mean ${\mathit{\mu }}_1^{\ast }$ for cases) and covariance matrix Σ. We assumed a common true covariance matrix for both groups. Due to the large number of parameter k = 2701 than the sample size n = 55, a shrinkage estimator for the covariance matrix was employed to estimate the pooled sample covariance matrix for the two groups based on the FADS data (Schafer and Strimmer 2005). When τ = 0 and ω = 1, the parameters ${\mathit{\mu }}_0^{\ast }$ and ${\mathit{\mu }}_1^{\ast }$ were equal to the sample mean vectors μ₀ and μ₁ in the FADS data respectively. To evaluate Type I errors, we set τ = 1, leading to no difference between the mean vectors for the two groups (i.e. ${\mathit{\mu }}_0^{\ast }-{\mathit{\mu }}_1^{\ast }=\mathbf{0}$). We evaluated power with τ varying from 0 to 1.

Thresholding to eliminate weak edges is a simple way in functional network analysis, since many of these connections are suspected to be spurious and their presence may obscure true signals. To mimic this practice, we set a thresholding parameter κ to discard weak edges, aiming to show how such a preprocessing procedure would influence analysis results. The threshold parameter value was selected based on the distribution of the correlation measures. Say, we generated 2701 × 55 number of edges in total for 55 subjects, then we selected some top significant edges based on their absolute values. For example, if κ = 0.8, we only preserved the 20% of the strongest edges and assigned 0 to the rest. After thresholding, we calculated several global network measures based on the corresponding binary networks too.

We also included a case with larger networks with 200 nodes and k = 200 × (200 − 1)/2 = 19900 connections. In addition to the original 2701 edges based on our real data, we augmented 19900–2701 edges having no differences between the two groups. Non-significant edge weights were independently generated from a Gaussian distribution with mean 0 and the smallest edge variance across all subjects in the FASD data.

Throughout the simulations, the test significance level was fixed at α = 0.05. The results were based on 1000 independent replicates for each set-up to estimate Type I error and power. 5000 permutations were used for NBS while 1000 for others.

We compared the performance of mass-univariate testing, logistic regression on global network measures, NBS, MDMR, SPU/aSPU and SPUw/aSPUw tests, and DiProPerm. We applied Fisher’s z-transformation to the Pearson correlations to obtain the weights for the edges of the networks. Binary networks were only used for calculating global network measures after thresholding was applied.

4.2 Main Results

We report empirical Type I error and power for the described statistical tests in the following. At τ = 1, we obtained empirical Type I error rates when each test was applied to data simulated under the null hypothesis of no group differences in network connectivity. Results for power were illustrated with varying τ < 1.

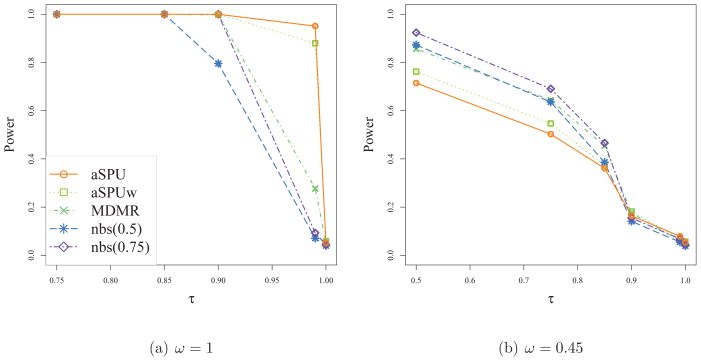
First, non-sparse networks were simulated to resemble the actual FASD data with ω = 1. All the tests had their Type I error rates close to the nominal level of 0.05 as shown in Table 3. We can see the influence of edge-wise differences between the two groups on power: as expected, increasing τ and thus decreasing the number of edges with changes between the two groups tended to decrease the power of every test The SPU test and SPUw test had greater power with an even γ than with an odd γ. This was due to the presence of both positive and negative connectivity differences in simulated data. As predicted by the theory, the SPU(2) test and MDMR performed similarly. Often the power of NBS increased as the predetermined threshold parameter increased in this given scenario: for instance nbs(0.75) showed greater power than nbs(0.1). This could be due to the existence of the clusters better detected by supra-thresholding with a larger thresholding parameter. Yet, this pattern was not always guaranteed since nbs(0.995) had lower power than nbs(0.99). When we had few edge-wise differences between cases and controls (i.e. when τ was large), the SPU(γ) or SPUw(γ) test with a larger γ was more powerful, leading to high power of the aSPU or aSPUw test. Overall, the aSPU test was the winner, closely followed by the aSPUw test. For example, at τ = 0.995 the power of the aSPU test was over 3 times of that of nbs(0.99). This suggests that the aSPU test might be preferred over NBS for network connectivity analysis when few edges show substantial differences between the two groups. Regardless of τ, the aSPU test showed greatest power when the simulated data resembled the FASD data with ω = 1.

Table 3.

Non-sparse networks with large differences between the two groups: empirical Type I error (for τ = 1) and power (for τ < 1) based on 1000 simulations.

ω	τ	SPU(1)	SPU(2)	SPU(3)	SPU(4)	SPU(5)	SPU(6)	SPU(7)	SPU(8)	SPU(∞)	aSPU
1	0.500	0.974	1.000	0.984	1.000	0.910	1.000	0.888	1.000	0.994	1.000
	0.750	0.832	1.000	0.959	1.000	0.885	1.000	0.875	1.000	0.993	1.000
	0.850	0.619	1.000	0.907	1.000	0.863	1.000	0.866	1.000	0.992	1.000
	0.900	0.449	1.000	0.864	1.000	0.855	1.000	0.880	1.000	0.988	1.000
	0.950	0.167	1.000	0.668	1.000	0.791	1.000	0.859	1.000	0.982	1.000
	0.975	0.097	0.810	0.550	1.000	0.752	1.000	0.846	1.000	0.965	0.999
	0.990	0.062	0.290	0.257	0.855	0.618	0.982	0.763	0.986	0.898	0.954
	0.995	0.056	0.145	0.155	0.479	0.457	0.813	0.627	0.883	0.762	0.757
	1.000	0.052	0.051	0.044	0.053	0.047	0.047	0.033	0.042	0.035	0.049

ω	τ	SPUw(1)	SPUw(2)	SPUw(3)	SPUw(4)	SPUw(5)	SPUw(6)	SPUw(7)	SPUw(8)	SPUw(∞)	aSPUw
1	0.500	0.977	1.000	0.997	1.000	0.987	1.000	0.952	1.000	0.994	1.000
	0.750	0.840	1.000	0.978	1.000	0.974	1.000	0.945	1.000	0.989	1.000
	0.850	0.609	1.000	0.942	1.000	0.945	1.000	0.919	1.000	0.985	1.000
	0.900	0.442	1.000	0.905	1.000	0.939	1.000	0.910	1.000	0.980	1.000
	0.950	0.137	0.994	0.644	1.000	0.828	1.000	0.848	1.000	0.967	1.000
	0.975	0.092	0.680	0.475	0.992	0.735	0.999	0.799	0.999	0.922	0.998
	0.990	0.053	0.212	0.183	0.601	0.483	0.897	0.642	0.956	0.806	0.889
	0.995	0.054	0.123	0.123	0.290	0.328	0.614	0.519	0.775	0.671	0.668
	1.000	0.050	0.052	0.048	0.047	0.049	0.047	0.042	0.045	0.052	0.058

ω	τ	MDMR	DiPP	nbs(0.1)	nbs(0.25)	nbs(0.5)	nbs(0.75)	nbs(0.9)	nbs(0.95)	nbs(0.99)	nbs(0.995)
1	0.500	1.000	1.000	0.985	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	0.750	1.000	0.998	0.761	0.963	1.000	1.000	1.000	1.000	1.000	1.000
	0.850	1.000	0.999	0.465	0.741	0.963	1.000	1.000	1.000	1.000	0.999
	0.900	1.000	0.994	0.296	0.495	0.784	0.977	1.000	1.000	1.000	0.998
	0.950	0.999	0.921	0.111	0.185	0.333	0.561	0.890	0.990	0.996	0.986
	0.975	0.803	0.590	0.074	0.095	0.144	0.245	0.457	0.719	0.884	0.815
	0.990	0.288	0.251	0.052	0.060	0.074	0.095	0.143	0.226	0.436	0.406
	0.995	0.140	0.143	0.045	0.053	0.059	0.067	0.083	0.124	0.191	0.131
	1.000	0.055	0.058	0.045	0.046	0.046	0.044	0.042	0.054	0.044	0.015

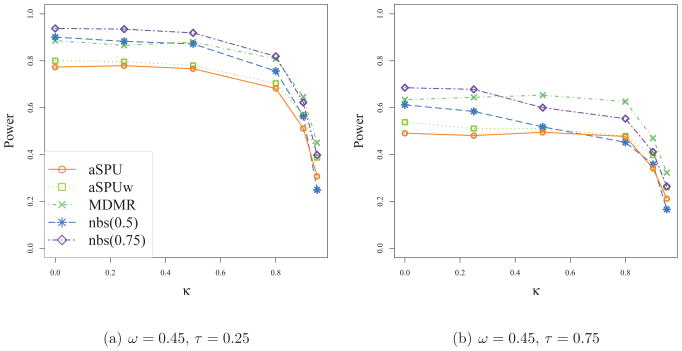
Next we investigated how the tests performed when we scaled down the magnitudes of network differences between the two groups by setting ω = 0.45 < 1. As shown in Table 4, the empirical Type I error rates of all the tests agreed well with the nominal one. As expected, the power of any test decreased as compared to Table 3. Increasing τ tended to decrease the power, as in Table 3. NBS performed best when τ = 0, 0.25, 0.50, 0.75, and 0.85, yet it showed relatively low power when τ = 0.95 and 0.99 where fewer edges had significant differences between cases and controls. Again the performance of NBS depended on the threshold parameter: as the threshold increased, the power went up, reaching the highest at nbs(0.75), then started decreasing with a larger threshold. The SPUw tests and thus the aSPUw test tended to perform better than the SPU tests and aSPU test respectively. The SPU(∞) test and SPUw(∞) test had low power in Table 4 due to the many smaller differences of network edges between the two groups.

Table 4.

Non-sparse networks with smaller differences: empirical Type I error (for τ = 1) and power (for τ < 1) based on 1000 simulations.

ω	τ	SPU(1)	SPU(2)	SPU(3)	SPU(4)	SPU(5)	SPU(6)	SPU(7)	SPU(8)	SPU(∞)	aSPU
0.45	0	0.545	0.888	0.514	0.872	0.378	0.797	0.300	0.636	0.194	0.780
	0.25	0.529	0.885	0.502	0.869	0.375	0.797	0.296	0.626	0.193	0.773
	0.50	0.470	0.844	0.468	0.833	0.340	0.760	0.277	0.597	0.186	0.716
	0.75	0.272	0.641	0.308	0.659	0.262	0.623	0.220	0.483	0.159	0.491
	0.85	0.156	0.450	0.226	0.488	0.212	0.463	0.204	0.383	0.143	0.357
	0.95	0.068	0.185	0.109	0.226	0.150	0.242	0.156	0.217	0.119	0.170
	0.99	0.058	0.074	0.066	0.088	0.082	0.093	0.075	0.096	0.079	0.086
	1.00	0.052	0.051	0.044	0.052	0.047	0.047	0.033	0.042	0.035	0.049

ω	τ	SPUw(1)	SPUw(2)	SPUw(3)	SPUw(4)	SPUw(5)	SPUw(6)	SPUw(7)	SPUw(8)	SPUw(∞)	aSPUw
0.45	0	0.586	0.897	0.596	0.897	0.519	0.855	0.422	0.787	0.212	0.801
	0.25	0.570	0.893	0.588	0.892	0.509	0.855	0.419	0.786	0.210	0.800
	0.50	0.501	0.861	0.540	0.853	0.477	0.824	0.403	0.748	0.199	0.750
	0.75	0.271	0.646	0.356	0.689	0.354	0.676	0.322	0.601	0.178	0.538
	0.85	0.148	0.448	0.237	0.494	0.260	0.502	0.255	0.465	0.158	0.387
	0.95	0.068	0.164	0.104	0.207	0.138	0.224	0.155	0.219	0.125	0.186
	0.99	0.055	0.073	0.065	0.078	0.068	0.086	0.072	0.075	0.081	0.078
	1.00	0.051	0.052	0.048	0.047	0.049	0.047	0.042	0.045	0.053	0.058

ω	τ	MDMR	DiPP	nbs(0.1)	nbs(0.25)	nbs(0.5)	nbs(0.75)	nbs(0.9)	nbs(0.95)	nbs(0.99)	nbs(0.995)
0.45	0	0.891	0.497	0.688	0.810	0.902	0.943	0.929	0.918	0.621	0.376
	0.25	0.886	0.492	0.672	0.800	0.901	0.938	0.927	0.915	0.608	0.356
	0.50	0.843	0.461	0.586	0.725	0.846	0.891	0.891	0.881	0.572	0.328
	0.75	0.634	0.370	0.351	0.462	0.612	0.685	0.739	0.724	0.443	0.238
	0.85	0.449	0.285	0.205	0.296	0.394	0.483	0.504	0.536	0.323	0.173
	0.95	0.176	0.156	0.086	0.110	0.149	0.165	0.202	0.219	0.162	0.080
	0.99	0.072	0.081	0.047	0.054	0.059	0.064	0.070	0.083	0.069	0.023
	1.00	0.055	0.060	0.042	0.047	0.048	0.039	0.043	0.052	0.043	0.013

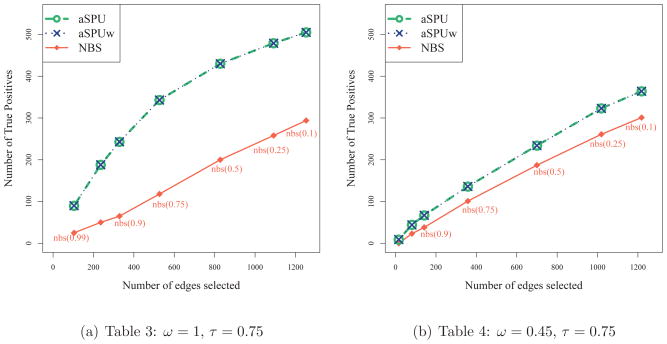
Although not the main point of this paper, we considered localizing changed connections between the two groups. As discussed earlier, NBS is attractive in that it can localize the connections as an evidence for the test significance, while the aSPU and aSPUw tests also can be used for edge selection. We applied NBS, aSPU and aSPUw tests to each of the simulated data sets corresponding to Tables 3 and 4. τ was set 0.75 so that the true positive edges being 25% of all the connections (i.e. 2701 × 0.25). Depending on the threshold being used, NBS selected different numbers of edges. Hence along with NBS, we examined how many true positive edges could be identified by the aSPU and aSPUw tests among a given number of their top ranked ones. As depicted in Figure 3, the aSPU and aSPUw tests showed better performance than NBS. For example in the case with ω = 1 and with 527 connections selected, NBS chose 118 true positives while both the aSPU and aSPUw tests selected 343.

Figure 3.

Edge selection.

In all simulation settings, the mass-univariate testing with the Bonferroni or FDR correction (at FDR=0.05 or 0.1), and the tests based on several global network measures performed extremely poorly. We presented their Type I error rates and power in Table 7. In addition, we replaced the logistic model with the probit model for the SPU and aSPU tests. The SPU and aSPU tests based on the probit model had power (Table 7) very close to that of the logistic model shown in Tables 3 and 4.

Table 7.

Non-sparse networks with large (ω = 1) and small (ω = 0.45) differences between the two groups: empirical Type I error (for τ = 1) and power (for τ < 1) based on 1000 simulations.

ω	τ	Probit model										FDR0.05	FDR0.1	Bonf	Network measures
		SPU(1)	SPU(2)	SPU(3)	SPU(4)	SPU(5)	SPU(6)	SPU(7)	SPU(8)	SPU(∞)	aSPU				CharPath	Eclust	Eglob	Eloc
1	0.500	0.973	1.000	0.984	1.000	0.911	1.000	0.889	1.000	0.993	1.000	0.000	0.008	0.000	0.056	0.041	0.057	0.045
	0.750	0.834	1.000	0.960	1.000	0.892	1.000	0.881	1.000	0.991	1.000	0.000	0.004	0.000	0.044	0.043	0.043	0.040
	0.850	0.612	1.000	0.901	1.000	0.865	1.000	0.874	1.000	0.990	1.000	0.000	0.002	0.000	0.044	0.040	0.041	0.039
	0.900	0.441	1.000	0.864	1.000	0.855	1.000	0.886	1.000	0.986	1.000	0.000	0.001	0.000	0.049	0.040	0.049	0.041
	0.950	0.159	1.000	0.670	1.000	0.793	1.000	0.861	1.000	0.978	1.000	0.000	0.001	0.000	0.048	0.044	0.048	0.046
	0.975	0.097	0.830	0.549	1.000	0.753	1.000	0.852	1.000	0.963	0.999	0.000	0.001	0.000	0.047	0.039	0.043	0.040
	0.990	0.063	0.309	0.261	0.870	0.625	0.985	0.767	0.986	0.899	0.954	0.000	0.000	0.000	0.047	0.044	0.046	0.044
	0.995	0.057	0.164	0.156	0.507	0.463	0.823	0.627	0.896	0.774	0.765	0.000	0.000	0.000	0.042	0.038	0.040	0.036
	1.000	0.044	0.057	0.046	0.059	0.051	0.050	0.039	0.045	0.037	0.044	0.000	0.000	0.000	0.042	0.041	0.041	0.036
0.45	0.00	0.553	0.905	0.517	0.886	0.392	0.809	0.312	0.659	0.203	0.783	0.000	0.000	0.000	0.047	0.050	0.044	0.050
	0.25	0.536	0.900	0.507	0.885	0.381	0.811	0.308	0.654	0.202	0.780	0.000	0.000	0.000	0.046	0.049	0.043	0.046
	0.50	0.464	0.871	0.469	0.851	0.353	0.784	0.288	0.625	0.195	0.721	0.000	0.000	0.000	0.047	0.049	0.046	0.047
	0.75	0.271	0.675	0.312	0.691	0.269	0.636	0.233	0.512	0.171	0.494	0.000	0.000	0.000	0.046	0.049	0.044	0.049
	0.85	0.152	0.474	0.223	0.517	0.219	0.499	0.215	0.406	0.153	0.357	0.000	0.000	0.000	0.040	0.042	0.041	0.044
	0.95	0.065	0.199	0.113	0.236	0.154	0.251	0.172	0.231	0.129	0.170	0.000	0.000	0.000	0.040	0.036	0.042	0.034
	0.99	0.054	0.085	0.066	0.095	0.085	0.103	0.073	0.102	0.083	0.081	0.000	0.000	0.000	0.040	0.035	0.041	0.034
	1.00	0.044	0.057	0.046	0.059	0.051	0.050	0.039	0.045	0.037	0.044	0.000	0.000	0.000	0.041	0.036	0.041	0.034

4.3 Sparse Networks

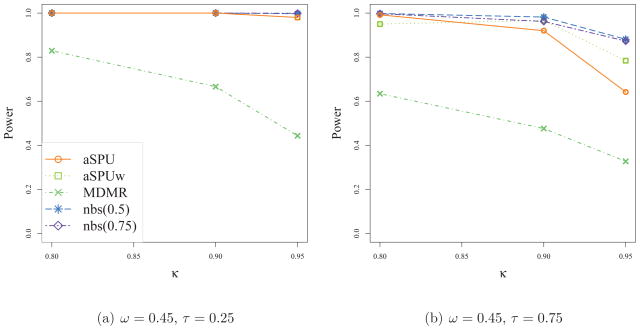
Figure 4 gives the results for case with true sparse networks. The parameters for general dissimilarity (ω = 1 or 0.45) and the proportion of changed edges (τ = 0 to 1) were set to be the same as in Tables 3 and 4. The edges were simulated to have weights with mean zero if edgewise-differences between the two groups were less than τ^th percentile in the FADS data. Overall, the power tended to slightly increase compared to Tables 3 and 4, but the patterns of relative power across the tests were similar to those observed in Tables 3 and 4. The sparsity of true networks did not appear to have any significant effect on the performance of any test.

Figure 4.

Sparse networks : empirical Type I error (for τ = 1) and power (for τ < 1) based on 1000 simulations.

4.4 Thresholding or Not?

As a preprocessing step, we applied thresholding to each network to create a sparse network before applying a test. As shown in Figure 5, power tended to decrease as thresholding parameter increased, implying no obvious gains from thresholding.

Figure 5.

Thresholding networks before applying a test: empirical power for detecting net-work differences with thresholding applied (κ > 0) or not applied (κ = 0).

4.5 Networks with Connection Changes in One Direction

The power of some tests depends on the direction or directions of the differences of the correlation measures between the two groups. In Figure 6, we simulated data based on the assumption that all edges from one group had weights no smaller than those from the other group. The power increased compared to those in Table 4. We did not include here, but it is noteworthy that among the SPU and SPUw tests, the SPU(1) and SPUw(1) were most powerful. In addition, as expected, the SPU(γ) test and SPUw(γ) test showed higher power when γ was odd than when it was even. As observed in Figure 6, the power tended to decrease with larger κ.

Figure 6.

Networks with edge weight changes in one direction: empirical power based on 1000 simulations.

4.6 Larger Networks with 200 nodes

Tables 5 and 6 show the results for cases with larger networks of 200 nodes. The general pattern in Table 5 is similar to that of Table 3. In Table 6, NBS is observed to lose power for larger networks as compared to its better results in Table 4. As expected, the performance of NBS critically depended on the threshold parameter, which however is difficult to specify in practice. Again it was confirmed that the SPU(2) test and MDMR performed similarly, while the SPU(4) test had the greatest power in this high-dimensional setting.

Table 5.

Networks of 200 nodes with large differences: empirical Type I error (for τ = 1) and power (for τ < 1) based on 1000 simulations.

ω	τ	SPU(1)	SPU(2)	SPU(3)	SPU(4)	SPU(5)	SPU(6)	SPU(7)	SPU(8)	SPU(∞)	aSPU
1	0.5	0.825	1.000	0.977	1.000	0.907	1.000	0.891	1.000	0.993	1.000
	0.75	0.534	1.000	0.941	1.000	0.884	1.000	0.876	1.000	0.993	1.000
	0.85	0.324	1.000	0.882	1.000	0.861	1.000	0.868	1.000	0.992	1.000
	0.95	0.101	0.994	0.618	1.000	0.791	1.000	0.856	1.000	0.983	1.000
	0.98	0.059	0.615	0.340	0.997	0.680	1.000	0.831	1.000	0.955	0.998
	0.999	0.039	0.069	0.068	0.113	0.185	0.280	0.318	0.390	0.420	0.308
	1	0.039	0.054	0.056	0.048	0.047	0.043	0.039	0.038	0.040	0.047

ω	τ	SPUw(1)	SPUw(2)	SPUw(3)	SPUw(4)	SPUw(5)	SPUw(6)	SPUw(7)	SPUw(8)	SPUw(∞)	aSPUw
1	0.5	0.613	1.000	0.891	1.000	0.892	1.000	0.857	1.000	0.783	1.000
	0.75	0.340	1.000	0.768	1.000	0.829	1.000	0.817	1.000	0.769	1.000
	0.85	0.213	1.000	0.606	1.000	0.757	1.000	0.762	1.000	0.753	1.000
	0.95	0.068	0.859	0.250	0.997	0.498	0.999	0.614	0.998	0.689	0.998
	0.98	0.052	0.353	0.116	0.737	0.258	0.932	0.426	0.958	0.590	0.888
	0.999	0.044	0.058	0.054	0.070	0.065	0.086	0.071	0.103	0.117	0.101
	1	0.045	0.047	0.053	0.045	0.055	0.047	0.047	0.041	0.048	0.055

ω	τ	MDMR	DiPP	nbs(0.1)	nbs(0.25)	nbs(0.5)	nbs(0.75)	nbs(0.9)	nbs(0.95)	nbs(0.99)	nbs(0.995)
1	0.5	1.000	0.910	0.728	0.942	1.000	1.000	1.000	1.000	1.000	1.000
	0.75	1.000	0.860	0.382	0.656	0.928	0.999	1.000	1.000	1.000	1.000
	0.85	1.000	0.693	0.223	0.399	0.692	0.949	1.000	1.000	1.000	0.999
	0.95	0.996	0.204	0.086	0.117	0.201	0.357	0.597	0.803	0.959	0.945
	0.98	0.609	0.063	0.070	0.106	0.141	0.199	0.299	0.532	0.490	0.100
	0.999	0.064	0.049	0.047	0.054	0.047	0.049	0.051	0.047	0.043	0.057
	1	0.051	0.053	0.051	0.049	0.050	0.047	0.045	0.047	0.043	0.038

Table 6.

Networks of 200 nodes with small differences: empirical Type I error (for τ = 1) and power (for τ < 1) based on 1000 simulations.

ω	τ	SPU(1)	SPU(2)	SPU(3)	SPU(4)	SPU(5)	SPU(6)	SPU(7)	SPU(8)	SPU(∞)	aSPU
0.45	0.25	0.288	0.846	0.429	0.857	0.371	0.796	0.293	0.642	0.190	0.712
	0.75	0.141	0.614	0.256	0.664	0.261	0.618	0.224	0.485	0.158	0.464
	0.95	0.064	0.171	0.100	0.224	0.147	0.236	0.156	0.224	0.121	0.167
	1	0.035	0.055	0.051	0.050	0.046	0.046	0.032	0.037	0.036	0.046

ω	τ	SPUw(1)	SPUw(2)	SPUw(3)	SPUw(4)	SPUw(5)	SPUw(6)	SPUw(7)	SPUw(8)	SPUw(∞)	aSPUw
0.45	0.25	0.193	0.680	0.214	0.649	0.164	0.564	0.131	0.417	0.087	0.508
	0.75	0.108	0.442	0.128	0.453	0.118	0.392	0.098	0.305	0.077	0.301
	0.95	0.056	0.138	0.066	0.151	0.065	0.146	0.065	0.132	0.068	0.106
	1	0.045	0.041	0.055	0.045	0.060	0.045	0.045	0.047	0.052	0.059

ω	τ	MDMR	DiPP	nbs(0.1)	nbs(0.25)	nbs(0.5)	nbs(0.75)	nbs(0.9)	nbs(0.95)	nbs(0.99)	nbs(0.995)
0.45	0.25	0.838	0.057	0.339	0.461	0.622	0.723	0.717	0.702	0.431	0.249
	0.75	0.612	0.065	0.174	0.253	0.354	0.473	0.476	0.452	0.315	0.164
	0.95	0.168	0.067	0.073	0.085	0.123	0.144	0.131	0.149	0.114	0.076
	1	0.054	0.055	0.049	0.047	0.056	0.047	0.046	0.045	0.043	0.038

5. DISCUSSION

In general, mass-univariate testing and network measure-based tests may not offer sufficient power to detect group differences in network connectivity. As a more powerful alternative, group differences can be determined by a global test that combines statistical evidence across many or all of the network edges. Since a global test does not test on each individual connection, if the null hypothesis is rejected, it cannot tell which individual connections give the significant difference. To deal with high-dimensionality of the data, each discussed global test calculates its p-values using resampling techniques without depending on questionable asymptotic assumptions.

Our simulation results show that the SPU/aSPU and SPUw/aSPUw tests are applicable to functional connectivity analyses, yielding respectable power compared to that of NBS across most simulations. In particular, in some situations (e.g. in Table 3 and Table 6), the SPU/aSPU and SPUw/aSPUw tests showed improved power over NBS. Nevertheless, in many situations, with an appropriate choice of the threshold parameter, NBS could perform better than the aSPU and aSPUw tests, which could be due to NBS’ exploiting the cluster structure in network differences. However, in practice, it may be difficult to choose an appropriate value for the threshold parameter in NBS, and strictly speaking, use of multiple threshold values in NBS requires a corresponding multiple testing adjustment. In contrast, the aSPU and aSPUw tests are easy to use; the overall result is given by the p-value of the aSPU or aSPUw test, while the p-values of other SPU or SPUw tests may shed light on the underlying association patterns. Following the idea of the aSPU and aSPUw tests, one may also combine the results of multiple NBS tests with multiple threshold values.

In summary, the aSPU and aSPUw tests can be complementary to NBS to test for group differences in functional connectivity. We hope that this study has introduced to the neuroimaging community some useful global tests and offered some practical guidelines for testing group differences in brain functional connectivity.

Highlights.

• Considering a key but yet largely neglected issue of testing for network differences;

• Introducing several new statistical tests drawn from other fields, e.g. genetics;

• Conducting extensive numerical studies to assess the power of the tests;

• Offering practical recommendations on the use of the tests.