Abstract
Three-dimensional reconstruction of large macromolecules like viruses at resolutions below 10 ÅA requires a large set of projection images. Several automatic and semi-automatic particle detection algorithms have been developed along the years. Here we present a general technique designed to automatically identify the projection images of particles. The method is based on Markov random field modelling of the projected images and involves a pre-processing of electron micrographs followed by image segmentation and post-processing. The image is modelled as a coupling of two fields—a Markovian and a non-Markovian. The Markovian field represents the segmented image. The micrograph is the non-Markovian field. The image segmentation step involves an estimation of coupling parameters and the maximum áa posteriori estimate of the realization of the Markovian field i.e, segmented image. Unlike most current methods, no bootstrapping with an initial selection of particles is required.
1. Introduction
Over the past decade cryo-transmission electron microscopy (Cryo-TEM) has emerged as an important tool, together with X-ray crystallography, to examine the three-dimensional structures and dynamic properties of macromolecules. Cryo-TEM specimen preparation procedures permit viruses and other macromolecules to be studied under a variety of conditions, which enables the functional properties of these molecules to be examined (Baker et al., 1999; Thuman-Commike and Chiu, 2000; van Heel et al., 2000). The three-dimensional model of a specimen is normally represented as a density function sampled at points of a regular grid. The images of individual particles in the electron micrograph are approximate projections of the specimen in the direction of the electron beam. The Projection Theorem that connects the Fourier Transform of the object with the transforms of its projections is used to construct the spatial density distribution of the particle (Crowther et al., 1970).
The initial step in three-dimensional structural studies of single particles and viruses after electron micrographs have been digitized is the selection (boxing) of particles images. Traditionally, this task has been accomplished by manual or semi-automatic procedures. However, the goal of greatly improving the solution of structure determinations to 8 ÅA or better comes with a requirement to significantly increase the number of images. Though 50 or fewer particle projections often suffice for computing reconstructions of many viruses in the 20–30 ÅA range (Baker et al., 1999), the number of particle projections needed for a reconstruction of a virus with unknown symmetry, at ~5 ÅA may increase by three orders of magnitude. Hence, the manual or semi-automatic particle identification techniques create a burdensome bottleneck in the overall process of three-dimensional structure determination (Nogales and Grigorieff, 2001). It is simply unfeasible to manually identify tens to hundreds of thousands of particle projections in low-contrast micrographs, and, even if feasible, the manual process is prone to errors.
At high magnification, noise in cryo-TEM micro-graphs of unstained, frozen hydrated macromolecules is unavoidable and makes automatic or semi-automatic detection of particle positions a challenging task. Since biological specimens are highly sensitive to the damaging effects of the electron beam used in cryo-TEM, minimal exposure methods must be employed and this results in very noisy, low-contrast images. A histogram of the density values in a typical cryo-TEM image illustrates that gray levels in the micrograph are concentrated in a very narrow range.
A difficult problem in automatic particle identification schemes is the so called labeling step, the process of associating a label with every pixel of the micrograph, e.g., a logical 1 if the pixel belongs to a projection of the virus particle and a logical 0 if the pixel belongs to the background. This process is generally described as segmentation, but, the more intuitive term labeling is often substituted. Once all pixels in the image are labeled, morphological filtering (Heijmans, 1994) followed by clustering (Martin et al., 1997) to connect together components with the same label can be used. Then, we may take advantage of additional information, if available, to increase the accuracy of the recognition process. In this paper we present a method of labeling based upon hidden Markov random field (HMRF) modelling combined with expectation maximization.
Our method lends itself nicely to automation because it does not require any parameters to be predetermined. For example, the Crosspoint method we introduced in (Martin et al., 1997) requires knowledge of the particle size and was restricted to the selection of spherical particles. A significant advantage of the method described here is that no prior knowledge regarding the size or shape of the particle is required.
2. Related work
Nicholson and Glaeser (2001) provide a comprehensive review of automatic particle selection algorithms and methods. Here we only outline methods of automatic particle selection we have implemented and also some that we investigated before considering the approach presented in this paper.
Automatic particle selection methods were first described by van Heel (1982). His method relies on computation of the local variance of pixel intensities over a relatively small area. The variance is calculated around each point of the image field and a maximum of the local variance indicates the presence of an object.
Several methods make use of a technique called template matching. In such algorithms a reference image is cross-correlated with an entire micrograph to detect the particles. The method proposed by Frank and Wagenkknecht (1983–84) uses correlation functions to detect the repeats of a motif. This approach is restricted to either a particular view of an asymmetric particle, or to any view of particles with high point group symmetry, such as icosahedral viruses. Cross-correlation procedures are also performed during the post-processing phase of the Crosspoint method presented in Martin et al. (1997).
Another class of automatic particle identification methods are feature-based. For example, the local and the global spatial statistical properties of the micrograph images are calculated in the method discussed in Lata et al. (1995). To isolate the particles and distinguish them from the noise, clustering based upon a discriminant analysis, in the feature space is then performed. This technique leads to many false positives.
Approaches based upon techniques developed in the computer vision field such as edge detection (Gonzales and Woods, 1996) are also very popular. Edges are significant cues to a transition from a view of the particle projection to the view of the background. Edges are generally signalled by changes in the gradient of the pixel intensity.
Consider for example the edge detector proposed by Canny (1986). The image is initially smoothed by Gaussian convolution with a kernel variance of σ. Then, a simple 2D first derivative operator is applied to the smoothed image to highlight regions of the image with high-valued first spatial derivatives. Edges give rise to ridges in the gradient magnitude image. A process known as non-maximal suppression is then applied wherein the algorithm tracks along the top of these ridges and sets to zero all pixels that are not actually on the ridge top, so as to give a thin line in the output. The tracking process is controlled by two thresholds, High > Low. Tracking can only begin at a point on a ridge higher than High. Tracking then continues in both directions out from that point until the height of the ridge falls below Low. This helps to ensure that noisy edges are not broken up into multiple edge fragments. The effect of applying a Canny edge detector with parameters Low = 0:03, High = 0:07, and σ = 3 to the image of frozen-hydrated virus particles is illustrated in Fig. 1.
Fig. 1.

The use of Canny edge detector. (A) Small field of view from an electron microscope of frozen hydrated virus particles. (B) Same as (A) after application of Canny edge detector. (C) The histogram of the pixel intensities in (A) illustrates the narrow dynamic range of pixel intensities.
The parameters of the Canny edge detector are generally selected on an ad hoc basis. Although the optimal values of parameters required by the edge detection algorithm may not vary much from one micrograph to another when the micrographs were collected under similar experimental conditions, nevertheless the ad hoc selection of the parameters is not very convenient.
Edges are significant cues to the presence of an object boundary. Thus, sometimes edge detection is used as a pre-processing step, as in the method proposed in Harauz and Lochovsky (1989). In this case the edges are further processed by spatial clustering. Particles are detected by symbolic processing of such a cluster of edge cues representing a particle. The approach taken by Zhu et al. (2001) is to first obtain an edge map of the micrograph consisting of the edge cues. The Hough transform is used to spatially cluster the edges to represent particles. The Hough transform is based upon a voting algorithm (Gonzales and Woods, 1996).
The signal-to-noise ratio (SNR), and in general the characterization of the noise in a micrograph, are very important to determine the best technique for automatic particle identification to be used for that micrograph. Noise estimation could help the automatic selection of the parameters of an edge detection algorithm.
Elder and Zucker (1998) describe a method of automatic selection of the reliable scales for the computation of the second order derivative of the intensity in the image field. A scale is assigned to each pixel for the computation of the second order spatial derivative. The noise is assumed to be additive white Gaussian. The idea is to select scales for each pixel that, given the magnitude of the standard deviation of the noise, are large enough to provide a reliable derivative estimate. If the second order derivative estimate at a pixel for a particular scale is below a threshold which is governed by the standard deviation of the noise, then the scale is increased until the second order derivative at such a scale exceeds the threshold. The only parameter required by this method is the standard deviation of the noise content. Thus, a procedure for the estimation of the standard deviation of the noise in micrographs would lead to an automatic edge detection algorithm.
Lee and Hoppel (1989) describe a fast method to compute the standard deviation of the noise in an image. This method is based upon two assumptions (a) identically distributed (i.i.d) noise, and (b) a linear noise model. This means independent zero mean additive noise and unit mean multiplicative noise. Consider the following random variables representing Z(a,b) is the observed intensity at the pixel with coordinates (a,b), X(a,b) is the noise free true intensity at the pixel with coordinates (a,b), W is a random variable that represents a zero mean additive i.i.d. noise with a standard deviation sw, and V is a random variable that represents a unit mean multiplicative noise with standard deviation sv. Then,
| (1) |
For a homogeneous block
| (2) |
| (3) |
| (4) |
thus
| (5) |
Thus, there is a linear relation between var (Z) and with the coefficients being the variances of the respective linear noise types—additive with sw and multiplicative with sv. The algorithm to estimate sw and sv consists of the following steps:
Divide the image into blocks of a given size, e.g., 4×4 or 8×8 pixels.
Compute the variance (i.e., var (Z)) and square of the means (i.e., ) of the pixel intensities in each block.
Use a least squares method to approximate a linear relation between the variances and the squares of the mean. A least square solution with negligible slope is indicative of an additive noise.
We illustrate the use of this method of noise estimation to detect Ross river virus particles in a micrograph. The edge detection algorithm is fully automatic. However, at larger variance of additive noise it has been observed that the algorithm fails to identify many edges and returns many spurious edges.
Fig. 2(B) shows the plot of var (Z) versus for the image in Figs. 2(A) and (C) shows the edges detected.
Fig. 2.
Edge detection of a micrograph of a frozen hydrated sample of Ross river virus: (A) A portion of the micrograph. (B) A plot of var (Z) versus Z2 for the micrograph (A) indicates an additive noise. (C) The edge map for (A). (D) Histogram of the pixel intensity distribution in (A).
These and similar experiments convinced us that edge detection methods are problematic for low-contrast, noisy electron micrographs. Also, experiments with isoconturing techniques (Song and Zhang, 2002) yielded discouraging results. Cross-correlation based techniques have recently been extended for selection of selection particles with unknown symmetry, or those that are asymmetric. We are also well aware of the limitations of semi-automatic techniques like our own Crosspoint method (Martin et al., 1997) and we were most interested in fully automatic techniques. Hence, after focusing our attention on methods that exploit the statistical properties of micrographs, we chose to study an HMRF scheme for particle selection.
3. Micrograph pre-processing based upon anisotropic diffusion
Often, an automatic particle identification method involves a pre-processing step designed to improve the SNR of a noisy micrograph. Various techniques, such as histogram equalization, and different filtering methods are commonly used. Now we describe briefly an anisotropic filtering technique we found very useful for enhancing the micrographs before the segmentation and labeling steps.
While other pre-processing techniques such as histogram equalization, attempt to increase the dynamic range of the low-contrast micrographs, the anisotropic diffusion may reduce this dynamic range, as seen in Fig. 3(C). The aim of anisotropic diffusion is to enhance the “edges” present in the image by smoothing the regions devoid of `edges.'
Fig. 3.
Anisotropic filtering. (A) A portion of a micrograph of frozen-hydrated Ross river virus particles. (B) Histogram of the pixel intensities in the micrograph displayed in (A). (C) The image in (A) after 10 cycles of anisotropic filtering. (D) Histogram of the pixel intensities in the micrograph displayed in (C).
A diffusion algorithm is used to modify iteratively the micrograph, as prescribed by a partial differential equations (PDE) (Perona and Malik, 1990). Consider for example the isotropic diffusion equation
| (6) |
In this partial differential equation t specifies an artificial time and ℓI is the gradient of the image. Let I(x,y) represent the original image. We solve the PDE with the initial condition I(x, y, 0)=I(x, y), over a range of t ∈ {0, T}. As a result, we obtain a sequence of filtered images indexed by t.
Unfortunately, this type of filtering produces an undesirable blurring of the edges of objects in the image. Perona and Malik (1990) replaced this classic isotropic diffusion equation with
| (7) |
where ∥ℓI∥ is the modulus of the gradient and g(∥ℓI∥) is the “edge stopping” function chosen to satisfy the condition g → 0 when ∥ℓI∥ → ∞.
The modified diffusion equation prevents the diffusion process across edges. As the gradient at some point increases sharply, signalling an edge, the value of the “edge stopping” function becomes very small making effectively zero. As a result, the intensity at that point on the edge of an object is unaltered as t increases. This procedure ensures that the edges do not get blurred in the process.
The result of applying ten iterations of anisotropic filtering to an electron micrograph of frozen-hydrated dengue virus particles is illustrated in Fig. 3. The efficacy of anisotropic diffusion is ascertained by the illustration in Fig. 4. Clearly a higher number of iterations benefits the quality of segmentation. However increasing the number of iterations is detrimental as it causes widespread diffusion resulting in joining of nearby projection in the segmentation output.
Fig. 4.
The effect of the number of iterations of anisotropic diffusion on segmentation, when all other parameters are kept constant. (A) A portion of a micrograph of frozen-hydrated Chilo Iridescent virus (CIV) particles. (B) Segmentation without anisotropic diffusion, (C) three iterations of anisotropic diffusion followed by segmentation (D) ten iterations of anisotropic diffusion followed by segmentation.
4. Informal presentation of the segmentation method
The essence of the method used for labeling pixels in a micrograph is now briefly introduced. It is well known that the temporal evolution of a physical process does not suffer abrupt changes and that the spatial properties of objects in a neighborhood exhibit some degree of coherence. Markov models are used to describe the evolution in time of memoryless processes, i.e., those processes whose subsequent states do not depend upon the prior history of the process. Such models are characterized by a set of parameters such as the number of states, the probability of a transition between a pair of states, and so forth.
Hidden Markov models exploit the “locality” of physical properties of a system and have been used in speech recognition applications (Rabiner, 1989) as well as object recognition in two dimensional images (Besag, 1986). The term “hidden” simply signifies the lack of direct knowledge for constructing the temporal or spatial Markov model of the object to be detected, e.g., the virus particle, or the physical phenomena to be investigated, e.g., the speech.
A classical example wherein a hidden Markov model is used to describe the results of an experiment involves the tossing of a coin in a location where no outside observer can witness the experiment itself, only the sequence of head/tail outcomes is reported. In this example, we can, for instance, construct three different models assuming that one, two, or three coins were used to generate the reported outcomes. The number of states and the probability of a transition between a pair of states are different for the three models. The information about the exact setup of the experiment, namely the number of coins used, is hidden: we are only told the sequence of head/tail outcomes.
Expectation maximization is a technique for selecting the parameters of the model that best fit the identifying information available. The more information we can gather, the more reliable we can expect the choice of model to be. Also, once the model is available, the more accurate the parameters of the model are. The digitized micrographs may constitute the only data available. It is not uncommon, for example, to have additional information such as a low resolution, preliminary 3D reconstruction of the object of interest. The extent of prior knowledge will vary among different applications and hence the model construction becomes application-dependent.
Hidden Markov techniques are often used to construct models of physical systems when the information about the system is gathered using an apparatus that distorts in some fashion the physical reality being observed. For example, images of macromolecules obtained using cryo-TEM methods are influenced by the contrast transfer function (CTF) characteristic of the imaging instrument and the conditions under which images are obtained, just as an opaque glass separating the observer from the individual tossing the coins prevents the former from observing the details of the experiment discussed above. This explains why hidden Markov techniques are very popular in virtually all experimental sciences.
The term “field” is used to associate the value of the property of interest with a point in a time-space coordinate system. For example, in a 2D image each pixel is described by two coordinates and other properties such as it's intensity, label, etc. In HMRF models, the field is constructed based upon a set of observed values. These values are related by an unknown stochastic function to the ones of interest to us. For example, a step in automatic particle selection is the labeling of individual pixels. Labeling means to construct the stochastic process X (i, j) describing the label (0 or 1) for the pixel with coordinates (i,j) given the stochastic process Y (i, j) describing the pixel intensity. The pixel intensities(are) observable, thus a model for Y (i, j) can be constructed.
Our interest in HMRF modelling was stimulated by the successful application of this class of methods to medical imaging. The diagnosis of abnormalities from MRI images (Zhang et al., 2001) based on HMRF modelling is used to distinguish between healthy cells and various types of abnormal cells, subject to the artifacts introduced by the MRI exploratory methods. These artifacts are very different than the ones introduced by an electron microscope. While the basic idea of the method is the same, the actual modelling algorithms and the challenges required to accurately recognize the objects of interest in the two cases are dissimilar. The most difficult problem we are faced with is the non-uniformity of the layer of ice in cryo-TEM micrographs.
5. Hidden Markov Random field models and expectation maximization
Image segmentation can be thought of as a labelling problem where the task is to label the image pixels as belonging to one of several groups. Particle selection amounts to a binary filtering operation, in that pixels are marked according to whether they belong to the particle or the background. Hence, such a segmentation could be thought of as labelling of the image field with labels picked up from a binary set {0,1}. Here we discuss the rationale for image segmentation based on the use of hidden Markov random field models and expectation maximization.
5.1. Markov random field models
Markov random field (MRF) theory provides a basis for modelling contextual constraints and allows us to formulate particle identification as an optimization problem. It is commonly accepted that the pixel intensities in a micrograph exhibit high spatial statistical interdependence, i.e., background pixels have a high probability of occurring next to other background pixels. Likewise, “particle” pixels generally lie adjacent to other “particle” pixels. The key assumption of a high spatial interdependence present in the image field can be easily incorporated into a Markov random field model.
5.1.1. Notations and basic assumptions
Given an experimental image, our goal is to assign a label to every pixel. We use the following notations:
L = {0, 1}—the set of labels.
D = {1, 2, …, d}—the set of quantized intensities in the observation field, i.e., the micrograph.
S = {1, 2, …, M}—the set of indices. R = {ri, i ∈ S} a family of random variables indexed by S.
r—a realization of R.
Let X and Y be random fields, where Y represents the observed field i.e., the micrograph, and X represents the segmented image. A realization of a random field is a set of values for all the elements of the field. For example, the realization of the field X consists of the set of labels (0 or 1) for every pixel. A realization of the field Y is the set of intensities for each pixel. We denote by x and y a particular realization of the two respective fields.
Let be the set of all realizations of the random field X, and similarly let be the set of all realizations of the random field Y.
and
The label assigned to the random variable xi determines the parameters of the distribution for the observed random variable yi
| (8) |
The function f is assumed to be normally distributed with mean μℓ and standard deviation σℓ, i.e.,
| (9) |
The assumption of a Gaussian functional form of distribution of intensities conditioned on pixel labels is based on the observations presented in Fig. 5. A histogram of intensities for portions of the background is shown in Fig. 5(A). Fig. 5(B) shows the corresponding histograms for projections of T4 prolate virus shown in Fig. 13. The two histograms resemble a Gaussian distribution.
Fig. 5.

The assumption of gaussian distribution of pixel intensities is supported by the experimental evidence from the histograms of pixel intensities belonging to the background and to particle projections. (A) The distribution of the background pixel intensities. All the pixels constituting the background should ideally be assigned the same label. (B) The distribution of the pixel intensities inside the projections of virus particles. All the pixels constituting one projection should ideally be assigned the same label, different from the one assigned to pixels from the background.
Fig. 13.
(A) Portion of a micrograph of frozen-hydrated bacteriophage T4 prolate virus. The virus does not have icosahedral symmetry. (B) The histogram of the pixel intensities for the image in (A). (C) The micrograph after anisotropic diffusion filtering. (D) Micrograph after the initialization step of HMRF. (E) Segmented micrograph. (F) Boxed particles in the micrograph.
5.1.2. MRF description
In an MRF, the sites in S are related to each other via a neighborhood system
where Ni is the set of neighbors of i
where d(i, j) is the distance between two sites. Note that a site not a neighbor of itself. An example of a second order neighborhood i.e., a neighborhood in which vertically, laterally, and diagonally adjacent sites are mutual neighbors, is presented in Fig. 6. The pixel marked x represents the center relative to which the neighborhood is defined. A clique is a subset of sites in S. c ⊆ S is a clique if every pair of distinct sites in c are neighbors. Single-site, pair-of-sites, triplets-of-sites cliques, and so on, can be defined, depending upon the order of the neighborhood.
Fig. 6.

Second order neighborhood. A single-site clique and four pair-of-sites cliques (top right) and four triple-site cliques (bottom right) for the second order neighborhood on the left.
A random field X is said to be an MRF on S with respect to a neighbor system N if and only if
and
The local characterization of the MRF defined above simply states that the probability that site i is assigned label xi depends only upon the neighborhood of i. The probability distribution P(x) is uniquely determined by the conditional probabilities. However, it is computationally very difficult to determine these characteristics in practice. We witness a computational explosion as the neighborhood size is even moderately increased.
The Hammersley–Clifford theorem establishes a relation between the MRF and the Gibbs distribution. The Gibbs Distribution relative to neighborhood system N has a probability measure given by
| (10) |
where Z is the normalizing constant or partition function given by
| (11) |
T, a constant called the temperature, is assumed to be 1 and U is the energy function
| (12) |
given by the sum of clique potentials over all possible cliques. C denotes the set of all possible cliques given a neighborhood. The set C consists of all the cliques corresponding to each site in the label field. Recall that the cliques have been defined as a part of Markov random fields for incorporating interaction between neighbors. As we shall see later, this may be used to ensure a smoothness in the variation of the labels.
Now we need to compute the probability of a particular realization x of X. The Hammersley–Clifford theorem ensures us such a means. It states that X is a MRF on S with respect to a neighbor system N if and only if X is a Gibbs random field on S with respect to the neighbor system N (Geman and Geman, 1984). This provides a simple way of specifying a joint probability for a realization with just the knowledge of conditional probability for a neighborhood at the points.
An auto logistic model (Li, 2001) is used to define the energy function for the MRF. With this function, the energy corresponding to
A single-site clique is a constant times the label of the pixel.
A two-sites clique is a constant negative quantity if the two sites have the same label. If the two are different, then the energy for that clique is a constant positive quantity.
As we will see later, the objective is to minimize the sum of energies of all the elements of the set of cliques, ensuring that Xi, a particular realization of the field of labels X, is smooth. However, the field X representing the segmented image must also be faithful to the measured data (the micrograph). Hence, we define a model of the image that should be integrated with the MRF model.
5.1.3. The image model
There are two random fields involved in the model of the image. The random field Y represents the observed image. Y is a random field that does not exhibit any neighborhood relationships, i.e., the random variables yi are independently distributed. The micrograph is a realization y of Y.
The random field X represents the segmented image and is assumed to exhibit MRF properties. The state of X is not observable. Given the state of Y, we wish to obtain the state of X. Furthermore, the two fields X and Y are coupled through a dependency (called emission distribution) where the parameters of the distribution of the random variable yi depend on the label assigned to the random variable xi. It may be recalled that the relation between yi and xi is
| (13) |
It is also assumed that given the label xi of Xi, the value taken up by the random variable Yi is independent of the values of other Xi's
| (14) |
Hence
| (15) |
where η = {ηℓ = {μℓ, ρℓ}, ∀ℓ ∈ L}.
Figs. 7(A) and (B) illustrate the relationship between the label field X and the image field Y. Labels from the set {0,1} have been assigned to the pixels of X in Fig. 7(A). For any pixel Xi in the label field X the intensity at the corresponding pixel Yi in Y follows a Gaussian distribution with its parameters indexed by the label. i.e., Xi “emits” Yi. Thus, the intensities in the image field Y are distributed according to a Gaussian distribution with parameters from the set {(μ0, ρ0), (μ1, ρ1)} depending whether Xi is 0 or 1.
Fig. 7.
An illustration of the relation between the image field and its corresponding label field. (A) The label field, X. (B) The image field, Y.
5.1.4. MRF estimation
The aim is to obtain the most likely realization of the segmentation field X given the observed field Y (the micrograph). If we represent the true labelling of the MRF X by and an estimate of it by x*, then the maximum a posteriori (MAP) estimate of x can be given by
| (16) |
But we know that
and
| (17) |
Hence maximizing P(y|x)P(x) is equivalent to minimizing
where,
| (18) |
Hence we need to find particular values for the field of random variables Xi such that the above function is minimized. A semi-optimal solution for minimization of this expression is obtained using the iterated conditional modes (henceforth I.C.M.) algorithm proposed by Besag (1986). The algorithm is based upon an iterative local minimization strategy where given the data, y, and the other labels , the algorithm sequentially updates each into by minimizing U(xi|y, xS−i).
5.2. Expectation maximization
Expectation maximization (Dempster et al., 1977) (henceforth E.M.) is a standard technique to estimate the parameters of a model when the data available are insufficient or incomplete. We start with an initial guess-estimate of the parameters and obtain an estimate of the “incomplete data” using these parameters. Once the “complete data” (along with some artificial data points) become available, the parameters of the model are estimated again to maximize the probability of occurrence of the “complete data”. Successive iterations result in increasingly more refined estimates of the parameters.
Let η(0) be the initial estimate of the parameters of the model. The E.M. algorithm consists of two major steps (Moon, 1996)
- Step 1: expectation—Calculate the expectation with respect to the unknown underlying variables using the current estimate of the variables, conditioned on the observations
In the above equation, t is an variable representing a particular iteration of the algorithm, Q is a function of the parameters set η conditioned on the parameter set obtained in the previous iteration and E(·) is the expectation function.(19) - Step 2: maximization—Calculate the new estimate of the parameters
(20)
The equations describing the application of E.M. to the image model are
| (20a) |
and
| (20b) |
where
| (20c) |
P(t)(ℓ|xNi) involves the MAP estimation as described earlier. The intermediate steps are described in detail in Zhang et al. (2001).
The refinement may be seen as an iterative optimization procedure where the parameters, namely μ0, ρ0, μ1, ρ1, and labels of the label field X are estimated using the E.M. algorithm. At this point it must be reemphasized that the iterative step of E.M. includes I.C.M. (Besag, 1986) which is a local optimization algorithm. Hence the initialization becomes a critical component of this technique. As illustrated in Figs. 8 and 12(D) and (E), the iterative refinement does not seem to affect the resulting segmentation substantially.
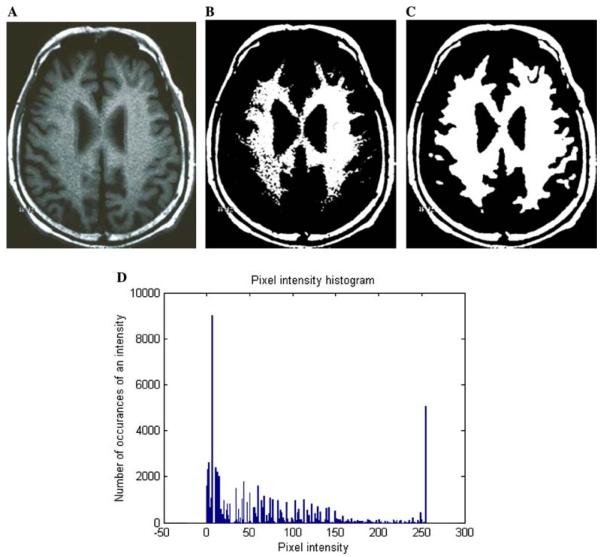
Fig. 8.
The effect of HMRF segmentation for an MRI image. (A) The MRI scan after anisotropic diffusion. (B) The image after initialization during the HMRF segmentation procedure. (C) The image after segmentation. (D) The Histogram of the pixel intensity of the sample image (A).
Fig. 12.
(A) A portion of a micrograph of frozen hydrated sample of Chilio Iridescent virus (CIV). (B) The histogram of the pixel intensities for the image in (A). (C) The micrograph after anisotropic diffusion filtering. (D) Micrograph after the initialization step of HMRF. (E) Segmented micrograph. (F) Boxed particles in the micrograph.
6. The HMRF-EM segmentation algorithm
First, we give an informal description of the method illustrated in Fig. 9 and then present the algorithm in detail. It is common practice to de-noise a noisy image before processing it for detection of cues such as edges. Very frequently some form of isotropic smoothing, e.g., Gaussian smoothing is used to achieve this. However, as noted earlier, such a method of smoothing leads to blurring of the important cues such as edges in addition to smoothing of the noise. Anisotropic diffusion (Perona and Malik, 1990; Weickert, 1998) is a form of smoothing that dampens out the noise while keeping the edge cues intact. Following is a stepwise description of the particle identification procedure.
Fig. 9.
The HMRF/EM-based automatic particle identification procedure introduced in this paper.
-
The image is split into rectangular blocks that are roughly twice the size of the projection of a particle. This is done to reduce the gradient of the background across each processed block. A high gradient degrades the quality of the segmentation process carried out in Step 3. The gradient of the background affects the algorithm in the following ways:
-
(a)The initialization is based solely on intensity histogram which encode only the frequencies of occurrence of any pixel intensity in the image. Due to the presence of a gradient, the contribution to the count of an intensity for example, may come from the background of a darker region, as well as from the inside of a projection of a virus in a brighter region. When the initialization is done for the entire image it performs poorly, as seen in Fig. 14.
-
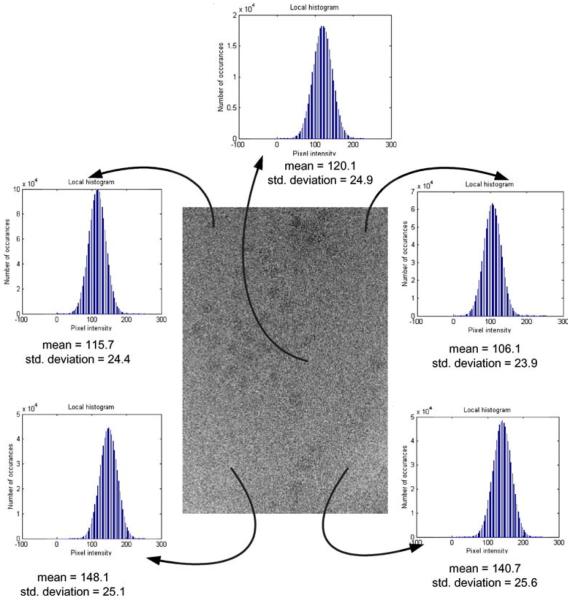
(b)The parameters μ0, σ0, μ1, σ1 are fixed for an image. However, as illustrated in Fig. 10, they are not the true parameters for intensity distribution across the whole image. The means and variances of pixel intensities are significantly different across the image due to the presence of the gradient. Cutting the image into blocks ensures a lack of drift in these parameters within each block.
An overlap among neighboring blocks is maintained. The size of overlap is the number of iterations of anisotropic diffusion. This is done to ensure the presence of pixel intensity information at the edges of the blocks during anisotropic diffusion filtering.
-
(a)
- As a pre-processing step individual blocks are filtered by means of anisotropic diffusion. Such filtering ensures that “edges” are preserved and less affected by smoothing (see Figs. 3(A) and (B)). The edge stopping function is
For each block we run 5 iteration of the algorithm. K = 0.2 to ensure the stability of the diffusion process.(22) - The blocks filtered through the anisotropic diffusion based filter are segmented using the HMRF method. The following steps are taken for segmentation.
-
(a)The initialization of the model is done using a discriminant measure based thresholding method proposed by Otsu (1979). The threshold is found by minimizing the intra-class variances and maximizing the inter-class variances. The resulting threshold is optimal (Otsu, 1979). Pixels with intensities below the threshold are marked with the label 1 indicating that they belong to the particle projection. The remaining pixels are marked with the label 0. This initialization is refined using the MRF based model of the image in Step 3(b).
-
(b)To refine the label estimates for each pixel within the MAP framework, we use the expectation maximization algorithm. A second order neighborhood, as the one in Fig. 6, is used. To compute the potential energy functions for cliques we use a auto logistic model. Four iterations of the algorithm are run for each block. The result of the segmentation is a binary image with one intensity for the particle projection and the other for the background.
-
(a)
Fig. 14.
The effect of initialization for a micrograph with a pronounced gradient. (A) A portion of an original micrograph of frozen-hydrated Ross river virus. (B) The micrograph after anisotropic diffusion. (C) The effect of the initialization for the HMRF segmentation algorithm for the micrograph in (A). (D) The segmented micrograph.
Fig. 10.
The effect of the gradient of the pixel intensity in a micrograph. The variation of the mean intensity of the background pixels across the micrograph image. The mean intensity of pixels within the projections of virus have a similar variation.
6.1. Boxing
Boxing means to construct a rectangle with a center co-located with the center of the particle. The segmentation procedure outlined above can be followed by different boxing techniques. We now discuss briefly the problem of boxing for particles with unknown symmetry.
Boxing particles with unknown symmetry is considerably more difficult than the corresponding procedure for iscosahedral particles. First, the center of a projection is well defined in case of icosahderal particle, while the center of the projection of an arbitrary 3D shape is more difficult to define. Second, the result of pixel labelling, or segmentation, is a shape with a vague resemblance to the actual shape of the projection. Typically, it consists of one or more clusters of marked pixels, often disconnected from each other, as we can see in Fig. 7(A). Recall that when the shape of the projection is known we can simply run a connected component algorithm, like the one described in Martin et al. (1997), and then determine the center of mass of the resulting cluster. In addition, we run a procedure to disconnect clusters corresponding to particle projections next to each other.
The post-processing of the segmented image to achieve boxing involves morphological filtering operations of opening and closing (Soille, 1999). These two morphological filtering operations are based on the two fundamental operations called dilation and erosion. For a binary labelled image, dilation is informally described as taking each pixel with value `1' and setting all pixels with value `0' in its neighborhood to the value `1.' Correspondingly, erosion means to take each pixel with value `1' in the neighborhood of a pixel with value `0' and re-setting the pixel value to `0.' The term “neighborhood” here bears no relation to the therm “neighborhood” in the framework of Markov Random Field described earlier. Pixels marked say as “1,” separated by pixels marked as “0” could be considered as belonging to the same neighborhood if they dominate a region of the image. The opening and closing operations can then be described as erosion followed by dilation and dilation followed by erosion, respectively.
The decision of whether a cluster in the segmented image is due to noise, or due to the projection of a particle is made according to the size of the cluster. For an icosahedral particle, additional filtering may be performed when the size of the particle is known. Such filtering is not possible for particles of arbitrary shape. A fully automatic boxing procedure is likely to report a fair number of false hits, especially in very noisy micrographs.
New algorithms to connect small clusters together based upon their size and the “distance” between their center of mass must be developed. Without any prior knowledge, about the shape of the particle boxing poses tremendous challenges. It seems thus natural to investigate a model based boxing method, an approach we plan to consider next.
The boxing of spherical particles in Figs. 11–13 in Section 7 is rather ad hoc and cannot be extended for particles of arbitrary shape. We run a connected component algorithm and then find the center of the particle and construct a box enclosing the particle.
Fig. 11.
(A) Portion of a micrograph of frozen-hydrated Ross river virus. (B) The histogram of the pixel intensities for the image in (A). (C) The micrograph after anisotropic diffusion filtering. (D) The micrograph after the initialization step of HMRF. (E) Segmented micrograph. (F) Boxed particles in the micrograph.
7. The quality of the solution and experimental results
We report on some results obtained with the method of automatic particle identification presented in this paper. Our first objective is a qualitative study based upon visual inspection of several micrographs and the results of particle “boxing.” We discuss several such experiments; in each case we present six images: the original, a pixel intensity histogram of the image, the image after preprocessing with anisotropic diffusion, image after the initialization step, the segmented image, and the image with particles boxed.
Once we are convinced that the method performs reasonably well, we consider a quantitative approach. The performance of a particle selection algorithm is sometimes benchmarked versus manual pickings by a trained human particle picker, although this metric is not universally accepted. The metrics used in this case are: the false positives rate and the false negatives rate. False positives occur when the algorithm “discovers” false or unwanted particles (“junk”). False negatives occur when the algorithm fails to identify genuine particle projections. The rates are given by the ratio of the corresponding false positive or false negative events to the total number of particles picked up by an experienced human particle picker.
The experiments we report were performed on micrographs of frozen-hydrated Ross river virus and the Chilo Iridescent virus (CIV) samples recorded in an FEI/Philips CM200 electron microscope. The results for a micrograph of Ross river virus is presented in Fig. 11. The size of the micrograph image is 5320 × 5992 pixels. The HMRF-EM segmentation algorithm followed by boxing as described earlier requires ≈1300 s to complete. The results for a micrograph of the Chilo Iridescent virus (CIV) is presented in Fig. 12. The size of the micrograph is 5425 × 5984 pixels. The HMRF-EM segmentation algorithm followed by boxing requires ≈1250 s to complete. The images were processed on a 1.6 GHz Pentium IV system with 512 MB main memory running Linux
Table 1 compares results obtained by manual selection and by the use of the HMRF algorithm. The present implementations of the HMRF algorithm produce a rather large false positive rate ~17% and false negative rate ~8%. The primary concern is with the relatively high false positive rate because incorrectly identified particle projections can markedly effect the quality of the overall reconstruction process.
Table 1.
The quality of the solution provided by the projection size based boxing algorithm on micrographs of viruses segmented using HMRF-EM algorithm
| Name of virus | Number of particles detected manually | Number of particles detected by MRF | False positives | False negatives |
|---|---|---|---|---|
| CIV | 277 | 306 | 55 | 26 |
| Ross river | 172 | 198 | 43 | 17 |
| T4 prolate | 95 | 104 | 16 | 7 |
Automatic selection of particle projections from a micrograph requires that the results be obtained reasonably fast. Hence, in addition to analysis pertinent to the quality of the solution, we report the time required by the algorithm for different size and number of particles in a micrograph. Table 2 lists the time devoted to different phases of our algorithm and demonstrates that pre-processing and segmentation account for 97–99% of the computing time. Since the pre-processing step has not yet been optimized, we are confident that significant efficiency can be realized after further algorithm development. Indeed, the rather large number of false positives (Table 1, column 4), demonstrates an inability to currently distinguish particles from junk. Clearly, the existing algorithm is unsuitable for real time electron microscopy which would allow the microscopist to record a very low magnification image at very low electron dose and from which it would be possible to assess particle concentration and distribution to aid high magnification imaging.
Table 2.
Time in seconds for the main processing steps of HMRF segmentation followed by the boxing algorithm based on projection size
| Name of virus | Image size | Anisotropic filtering | Initialization | MRF segmentation | Boxing | Total |
|---|---|---|---|---|---|---|
| CIV | 1174×940 | 17 | 3 | 20 | 2 | 42 |
| Ross river virus | 2340×2235 | 281 | 28 | 432 | 15 | 756 |
| CIV | 5457×6000 | 560 | 43 | 701 | 28 | 1332 |
| CIV | 8768×11381 | 2102 | 208 | 2804 | 142 | 5256 |
The programs were run on a 1.6GHz Pentium IV system with 512MB main memory running Linux.
Finally, Fig. 13 shows the results of applying our procedure to an asymmetric structure, the prolate capsid of the bacteriophage T4.
8. Conclusions and future work
The HMRF particle selection algorithm does not assume any particular shape or size for the virus projection. Even though most of our experiments were performed with micrographs of symmetric particles the one illustrated in Fig. 13 for an asymmetric particle, gives us confidence in the ability of our algorithm to identify particles of any shape.
However, several aspects of particle selection processing demand improvement. First, the algorithm is computationally intensive. The time for automatic particle selection is hundreds of seconds for a 6000× 6000 pixel micrograph with some 50–70 particles.
A significant portion of the time is spent in obtaining an optimization for the MRF. This can be overcome if a multi-scale technique is adopted. With a multi-scale technique, a series of images of smaller size, with larger pixel dimensions, are constructed. The optimization starts with the smallest size image, corresponding to the largest scale. The results are propagated to the optimization for the same image but of larger size, at next scale. Multi-scale MRF techniques are already very popular within the vision community (Bouman and Shapiro, 1994).
More intelligent means of distinguishing a projection of the virus from the projection due to noise could be introduced such as some discrimination method based on features of the projection more informative than mere projection size. Such features can be extracted from projections of the lower resolution 3D map of the particle.
The ICM algorithm performs a local optimization of the Markov random field and it is very sensitive to initialization. Global optimization methods like simulated annealing (Kirkpatrick et al., 1983) are likely to produce better results, but would require a fair amount of CPU cycles and, thus, increase the processing time.
The effect of initialization for the micrograph in Fig. 14(A) with a pronounced gradient of the background is captured by the image in Fig. 14(B). The final segmentation for the micrograph in Fig. 14(A) is presented in Fig. 14(C).
High pass filtering may be used to remove the background gradient. However, this does not perform very well if the background has a steep gradient. The other possible solution is to work on smaller regions where the background gradient is expected to vary gradually. Still another way to work around this is to use a multi-scale technique, the solution we are currently working on.
Current work is focussed on the following problems:
Construct a better “edge stopping” function for the anisotropic diffusion equation to improve noise smoothing operations.
Use a multi-scale Markov random field to reduce the computation time and make the algorithm more robust to initialization.
Use low resolution 3D reconstruction maps to enhance the identification of particles and their distinction from “junk.”
Alone, the metrics discussed in this paper does not allow us to compare different techniques. To reliably compare various automatic particle identification methods we need a standard benchmark. Once the benchmark becomes available, researchers proposing a new algorithm may test it using benchmark micrographs and draw conclusions regarding the results produced by the new algorithm versus other algorithms.
This standard benchmark should consist of:
-
(a)
a set of micrographs as well as meta-information about each micrograph,
-
(b)
procedures in several programming languages to read an image into a two-dimensional array, and
-
(c)
a database of results obtained for each micrograph. The results should be in some standard format to allow a rapid comparison between different methods. These results should refer to the quality of the solution as well as the time required to process the micrograph.
The meta-information available for each micrograph should include items such as
-
(i)
the size of the image,
-
(ii)
the “true” number of particles present in the micro-graph, and the coordinates of the “box” for each particle,
-
(iii)
the noise characterization of the micrograph,
-
(iv)
the contrast level, derived from the histogram of the micrograph,
-
(v)
a measure of the non-uniformity of the layer of ice in the image, possibly given by a gradient function,
-
(vi)
information regarding the type of the microscope and the experimental setup used to collect the image.
The metrics used to compare different methods should summarize the results of a comparative analysis of a new method applied to all images from the benchmark suite. A non-exhaustive list of such metrics includes
-
(a)
The expected value and the variance of ratio of particle identified by the method versus the number of “true” particles.
-
(b)
The expected value and the variance of the number of “false positives”.
-
(c)
A measure of the quality of the solution, for example the average error in determining the center of each particle.
We are in the process of developing such a benchmark suite. Our effort can only be successful if supported by the entire community with additional images as well the as results obtained with different methods. Ideally, the source code for each method should be made available, so the results obtained by an individual can be confirmed by other researchers.
Once a database of such results is available, then we can identify the method(s) best suited for automatic identification for different classes of micrographs.
It seems reasonable to assume that given a large collection of micrographs, different automatic identification methods will perform differently on different images of the benchmark suite. One method is likely to outperform others on images with some characteristics and, in turn, be outperformed by other methods on images with different characteristics. Ultimately, hybrid techniques are likely to prevail.
Acknowledgments
We thank W. Zhang and X. Yan for supplying image data and Y. Ji for help in constructing the benchmark suite. The authors express their gratitude for the constructive comments of the anonymous reviewers. The study was supported in part by the National Science Foundation Grants MCB9527131 and DBI0296107 to D.C. Marinescu and T.S. Baker, and ACI0296035 and EIA0296179 to D.C. Marinescu.
References
- Baker TS, Olson NH, Fuller SD. Adding the third dimension to virus life cycles: three-dimensional reconstruction of icosahedral viruses from cryo-electron micrographs. Microbiol. Mol. Biol. Rev. 63(4):862–922. doi: 10.1128/mmbr.63.4.862-922.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Besag J. On the statistical analysis of dirty pictures. J. R. Stat. Soc. 48(3):259–302. [Google Scholar]
- Bouman C, Shapiro M. A multiscale random field model for Bayesian image segmentation. IEEE Trans. Image Process. 3(2):162–177. doi: 10.1109/83.277898. [DOI] [PubMed] [Google Scholar]
- Canny J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 8(6):679–697. [PubMed] [Google Scholar]
- Crowther RA, DeRosier DJ, Klug A. The reconstruction of a three-dimensional structure from projections and its application to electron microscopy. Proc. R. Soc. Lond. A. 317:319–340. doi: 10.1098/rspb.1972.0068. [DOI] [PubMed] [Google Scholar]
- Dempster AP, Laird NM, Rubin DB. Maximal likelihood form incomplete data via the EM algorithm. J. R. Stat. Soc. B. 39:1–38. [Google Scholar]
- Elder JH, Zucker SW. Local scale control for edge detection and blur estimation. IEEE Trans. Pattern Anal. Mach. Intell. 20(7):699–716. [Google Scholar]
- Frank J, Wagenkknecht T. Automatic selection of molecular images from electron micrographs. Ultramicroscopy. 1983–84;2(3):169–175. [Google Scholar]
- Geman S, Geman D. Stochastic relaxation, Gibbs distributions and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 6:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- Gonzales RC, Woods RE. Digital Image Processing. Prentice Hall; Englewood Cliff, NJ: [Google Scholar]
- Harauz G, Lochovsky FA. Automatic selection of macromolecules from electron micrographs. Ultramicroscopy. 31:333–344. doi: 10.1016/0304-3991(89)90331-8. [DOI] [PubMed] [Google Scholar]
- Heijmans HJAM. Morphological image operators. Academic Press; Boston: [Google Scholar]
- Lee JS, Hoppel K. Noise modeling and estimation of remotely sensed images. Proc. International Geoscience and Remote Sensing. 1989;2:1005–1008. 1989. [Google Scholar]
- Kirkpatrick S, Gelart CD, Jr., Vecchi MP. Optimization by simulated annealing. Science. 31:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- Li SZ. Markov Random Field Models in Computer Vision. Springer-Verlag; Berlin: [Google Scholar]
- Martin IAB, Marinescu DC, Lynch RE, Baker TS. Identification of spherical virus particles in digitized images of entire electron micrographs. J. Struct. Biol. 120:146–157. doi: 10.1006/jsbi.1997.3901. [DOI] [PubMed] [Google Scholar]
- Moon TK. The expectation maximization algorithm. IEEE Signal Proc. Mag. :47–59. [Google Scholar]
- Nicholson WV, Glaeser RM. Review: automatic particle detection in electron microscopy. J. Struct. Biol. 133:90–101. doi: 10.1006/jsbi.2001.4348. [DOI] [PubMed] [Google Scholar]
- Nogales E, Grigorieff N. Molecular machines: putting the pieces together. J. Cell Biol. 152:F1F10. doi: 10.1083/jcb.152.1.f1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otsu N. A threshold selection method from gray level histogram. IEEE Trans. Systems Man Cybernet. SMC-8:62–66. [Google Scholar]
- Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 12(7):629–639. [Google Scholar]
- Rabiner LR. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE. 77(2):257–286. [Google Scholar]
- Lata KR, Penczek P, Frank J. Automatic particle picking from electron micrographs. Ultramicroscopy. 58:381–391. doi: 10.1016/0304-3991(95)00002-i. [DOI] [PubMed] [Google Scholar]
- Soille P. Morphological Image Analysis: Principles and Applications. Springer-Verlag; Berlin: [Google Scholar]
- Song Y, Zhang A. Monotonic Trees. 10th International Conference on Discrete Geometry for Computer Imagery.2002. pp. 114–123. [Google Scholar]
- Thuman-Commike PA, Chiu W. Reconstruction principles of icosahedral virus structure determination using electron cryomicroscopy. Micron. 31:687–711. doi: 10.1016/s0968-4328(99)00077-3. [DOI] [PubMed] [Google Scholar]
- van Heel M. Detection of objects in quantum-noise-limited images. Ultramicroscopy. 7(4):331–341. [Google Scholar]
- van Heel M, Gowen B, Matadeen R, Orlova EV, Finn R, Pape T, Cohen D, Stark H, Schmidt R, Schatz M, Patwardhan A. Single-particle electron cryo-microscopy: towards atomic resolution. Quart. Rev. Biophys. 33(4):307–369. doi: 10.1017/s0033583500003644. [DOI] [PubMed] [Google Scholar]
- Weickert J. Anisotropic Diffusion in Image Processing. Teubner-Verlag; [Google Scholar]
- Zhang Y, Smith S, Brady M. Segmentation of brain MRI images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans. Med. Imag. 20(1):45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]
- Zhu Y, Carragher B, Kriegman D, Milligan RA, Potter CS. Automated identification of filaments in cryoelectron microscopy images. J. Struct. Biol. 135(3):302–312. doi: 10.1006/jsbi.2001.4415. [DOI] [PubMed] [Google Scholar]