Abstract
Relative risks (RRs) are often considered the preferred measures of association in prospective studies, especially when the binary outcome of interest is common. In particular, many researchers regard RRs to be more intuitively interpretable than odds ratios. Although RR regression is a special case of generalized linear models, specifically with a log link function for the binomial (or Bernoulli) outcome, the resulting log-binomial regression does not respect the natural parameter constraints. Because log-binomial regression does not ensure that predicted probabilities are mapped to the [0,1] range, maximum likelihood (ML) estimation is often subject to numerical instability that leads to convergence problems. To circumvent these problems, a number of alternative approaches for estimating RR regression parameters have been proposed. One approach that has been widely studied is the use of Poisson regression estimating equations. The estimating equations for Poisson regression yield consistent, albeit inefficient, estimators of the RR regression parameters. We consider the relative efficiency of the Poisson regression estimator and develop an alternative, almost efficient estimator for the RR regression parameters. The proposed method uses near-optimal weights based on a Maclaurin series (Taylor series expanded around zero) approximation to the true Bernoulli or binomial weight function. This yields an almost efficient estimator while avoiding convergence problems. We examine the asymptotic relative efficiency of the proposed estimator for an increase in the number of terms in the series. Using simulations, we demonstrate the potential for convergence problems with standard ML estimation of the log-binomial regression model and illustrate how this is overcome using the proposed estimator. We apply the proposed estimator to a study of predictors of pre-operative use of beta blockers among patients undergoing colorectal surgery after diagnosis of colon cancer.
Keywords: Bernoulli likelihood, Convergence problems, Maclaurin series, Poisson regression, Quasi-likelihood
1. Introduction
We consider prospective study designs where it is of scientific interest to estimate relative risks (RRs) conditional on covariates. Interestingly, in many studies where RRs are the parameters of primary scientific interest, odds ratios (ORs) are reported instead. This can be explained in part by the technical advantages of logistic regression (e.g. no constraints on the regression parameters) and the widespread availability of appropriate software. Although RR regression is a special case of generalized linear models, specifically with a log link function for the binomial (or Bernoulli) outcome, the resulting log-binomial regression does not respect the natural parameter constraints. Because log-binomial regression does not ensure that predicted probabilities are mapped to the [0,1] range, maximum likelihood (ML) estimation is often subject to numerical instability that leads to convergence problems. It has been noted by several authors that convergence problems are especially likely to arise when the predicted probabilities are close to 1 (Wacholder, 1986; Lu and Tilley, 2001; Zou, 2004; Carter and others, 2005). Several approaches have been proposed to circumvent the convergence problems associated with ML estimation of log-binomial regression. These include: (1) directly estimating RR using a constrained ML method that truncates the range of the probabilities (Wacholder, 1986); (2) adding a small constant to each subject's Bernoulli outcome in the sample (Clogg and others, 1991; Deddens and others, 2003); (3) indirectly estimating RR using the mathematical relationship between OR and RR for a single binary covariate (Zhang and Yu, 1998); and (4) quasi-likelihood method of moments techniques (Traissac and others, 1999; McNutt and others, 2003; Zou, 2004; Carter and others, 2005).
One approach that has been widely studied is the use of Poisson regression estimating equations (Traissac and others, 1999; McNutt and others, 2003; Zou, 2004; Carter and others, 2005). That is, the Poisson likelihood equations are used to estimate the RR regression parameters without constraints. The estimating equations for Poisson regression yield consistent, asymptotically normal (CAN) estimators of the RR regression parameters. Moreover, Carter and others (2005) found that they alleviate convergence problems associated with ML estimation of log-binomial regression parameters. Although estimating equations for Poisson regression yield consistent estimators of the RR regression parameters, they are inefficient because the “weight function” is misspecified as Poisson instead of bionomial or Bernoulli. As we demonstrate later, the loss of efficiency tends to be greatest in the very setting where their use is required, i.e. when predicted probabilities are far from zero.
We consider the relative efficiency of the Poisson regression estimator and develop an alternative, almost efficient estimator for the RR regression parameters. The proposed method uses near-optimal weights based on a Maclaurin series (Taylor series expanded around 0) approximation to the true Bernoulli weight function. If the Maclaurin series is truncated at its first term, this yields the Poisson regression estimator. Truncation at higher terms in the series yields near-optimal weights and almost efficient estimators. Using method-of-moments, assuming the RR regression model is correctly specified, the estimators are consistent for any given truncation of the Maclaurin series approximation to the optimal weight function. We examine the asymptotic relative efficiency (ARE) for an increase in the number of terms in the series. We also make recommendations for choice of the number of terms to avoid similar finite sample convergence problems as with ML estimation of log-binomial regression parameters. We present results of a simulation study that highlight the potential gains in efficiency in finite samples.
The proposed method is motivated by a study of best practices for patients undergoing surgery for colorectal cancer (Arriaga and others, 2009). A panel of colorectal and general surgeons was assembled to ascertain a set of 37 evidence-based practices that they considered to be the most pertinent to the evaluation and management of a patient undergoing colorectal surgery after diagnosis of colon cancer. Patients with known heart disease who are given beta blockers prior to surgery have been found to have a significantly reduced risk of post-operative death (Poldermans and others, 1999). Thus, one of the key practices is giving beta blockers when indications (heart disease) are present. In this study, the medical records of 210 cancer patients with cardiac conditions from three hospitals were reviewed (due to confidentiality, hospital names must remain anonymous). Here the binary outcome of interest is whether the patient was given beta blockers (yes, no) prior to surgery. Upon review of the medical records, it was found that beta blockers were given to 130 out of the 210 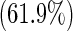 patients, indicating that many doctors are not meeting the best practices guideline for almost
patients, indicating that many doctors are not meeting the best practices guideline for almost  of the patients. The goal of this study is to determine predictors of pre-operative use of beta blockers in these patients. The main predictors of interest are the patient's age (in years), race (categorized as white versus other), gender, number of comorbidities, and “American Society of Anesthesiologists (ASA) score.” The ASA score is a global assessment of the physical status of the patient (Owens and others, 1978) and yields a two-level indicator of a patient's pre-operative disease status at diagnosis (
of the patients. The goal of this study is to determine predictors of pre-operative use of beta blockers in these patients. The main predictors of interest are the patient's age (in years), race (categorized as white versus other), gender, number of comorbidities, and “American Society of Anesthesiologists (ASA) score.” The ASA score is a global assessment of the physical status of the patient (Owens and others, 1978) and yields a two-level indicator of a patient's pre-operative disease status at diagnosis (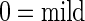 disease,
disease, 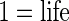 -threatening disease). Table 1 presents the overall distributions of beta blocker use, age, race, gender, number of comorbidities, and ASA score. Although all of these cardiac patients should receive pre-operative beta blockers, it is of interest to explore whether pre-operative disease status (ASA score), age, race, gender, and number of comorbidities are predictive of those patients who were given beta blockers. The study investigators conjectured that patients with higher risks of complications, i.e. patients who are older, with worse ASA score and more comorbidities, are more likely to receive pre-operative beta blockers. It is also of interest to examine whether there are any differences by race and gender.
-threatening disease). Table 1 presents the overall distributions of beta blocker use, age, race, gender, number of comorbidities, and ASA score. Although all of these cardiac patients should receive pre-operative beta blockers, it is of interest to explore whether pre-operative disease status (ASA score), age, race, gender, and number of comorbidities are predictive of those patients who were given beta blockers. The study investigators conjectured that patients with higher risks of complications, i.e. patients who are older, with worse ASA score and more comorbidities, are more likely to receive pre-operative beta blockers. It is also of interest to examine whether there are any differences by race and gender.
Table 1.
Descriptive statistics for patient characteristics from study of pre-operative use of beta blockers among patients undergoing colorectal surgery
| Variable | Level | Number ( ) ) |
|---|---|---|
| Pre-operative beta blockers | Yes | 130 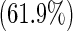
|
| No | 80 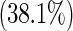
|
|
| ASA score | 0 | 92 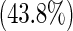
|
| 1 | 118 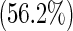
|
|
| Gender | Male | 98 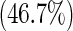
|
| Female | 112 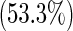
|
|
| Race | White | 182 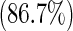
|
| Other | 28 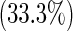
|
|
| Number of comorbidities | 0 | 30 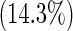
|
| 1 | 62 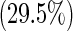
|
|
| 2 | 58 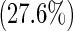
|
|
| 3 | 36 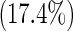
|
|
| 4 | 17 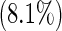
|
|
| 5 | 4 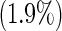
|
|
| 6 | 3 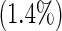
|
|
| Age, median (range) | 68.5 (26–95) |
In Section 2, we describe the RR regression model, the corresponding Bernoulli likelihood, and the proposed estimating equations for the RR regression parameters. In Section 3, we present results of a study examining the ARE of the proposed estimator for increasing number of terms in the series. In Section 4, we present results of a simulation study that demonstrate the potential gains in efficiency in finite samples.
2. RR regression model
Let 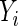 denote the binary response (success or failure) for subject
denote the binary response (success or failure) for subject 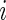 ,
, 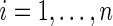 , where
, where 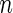 is the number of independent subjects. Then
is the number of independent subjects. Then 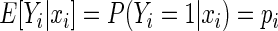 is the success probability, where
is the success probability, where 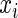 is a
is a 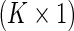 vector of covariates. In RR regression, the success probability is modeled using the log link,
vector of covariates. In RR regression, the success probability is modeled using the log link,
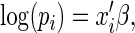 |
or, equivalently, 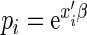 , where
, where 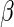 is the vector of regression parameters. One can easily show that the elements of
is the vector of regression parameters. One can easily show that the elements of 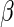 (with the exception of the intercept) have interpretation as log-RRs (see, for example, Jewell, 2003). For the remainder of this paper, we assume that the main interest centers on estimating the regression parameter vector
(with the exception of the intercept) have interpretation as log-RRs (see, for example, Jewell, 2003). For the remainder of this paper, we assume that the main interest centers on estimating the regression parameter vector 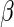 .
.
The Bernoulli likelihood is
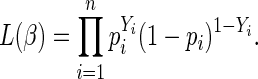 |
(2.1) |
The ML estimating equations for 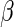 are
are 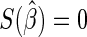 , where
, where
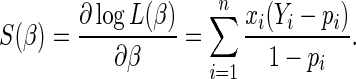 |
(2.2) |
The MLE is the asymptotically efficient estimate. However, when the success probability approaches 1, the denominator of (2.2) approaches 0, resulting in convergence problems. Wacholder (1986) constrained the likelihood to prevent 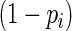 from approaching 0; however, these modifications are still subject to convergence problems (Baumgarten and others, 1989).
from approaching 0; however, these modifications are still subject to convergence problems (Baumgarten and others, 1989).
In general, to estimate 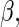 one can use estimating equations (or quasi-likelihood equations; Wedderburn, 1974) of the form
one can use estimating equations (or quasi-likelihood equations; Wedderburn, 1974) of the form 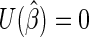 , where
, where
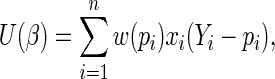 |
(2.3) |
with 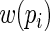 being a “weight” function of
being a “weight” function of 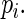 Assuming that the regression model for
Assuming that the regression model for 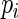 has been correctly specified, i.e.
has been correctly specified, i.e. 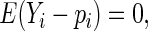 these estimating equations yield CAN estimators of
these estimating equations yield CAN estimators of 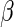 for any bounded weight function
for any bounded weight function 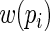 (see, for example, Rotnitzky, 2009). Specifically, it can be shown that the asymptotic distribution of
(see, for example, Rotnitzky, 2009). Specifically, it can be shown that the asymptotic distribution of 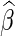 , the estimator for
, the estimator for 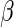 with a particular choice of
with a particular choice of 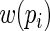 , satisfies
, satisfies
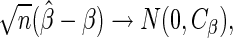 |
(2.4) |
where
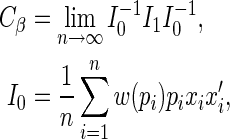 |
and
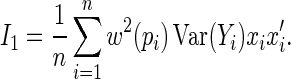 |
Note that the asymptotically efficient estimate is the MLE, with weight function 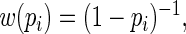 and asymptotic covariance determined by
and asymptotic covariance determined by 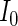 . Consistent estimators of the asymptotic covariance of the estimated regression parameters can be obtained using the empirical estimator of
. Consistent estimators of the asymptotic covariance of the estimated regression parameters can be obtained using the empirical estimator of 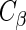 proposed by Huber (1967), White (1982), and Royall (1986). The empirical variance estimator is obtained by evaluating
proposed by Huber (1967), White (1982), and Royall (1986). The empirical variance estimator is obtained by evaluating 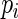 at
at 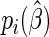 and substituting
and substituting 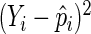 for
for 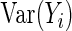 ; this is widely known as the sandwich variance estimator.
; this is widely known as the sandwich variance estimator.
The use of Poisson regression for estimating 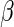 has received much attention recently (e.g. Traissac and others, 1999; McNutt and others, 2003; Zou, 2004; Carter and others, 2005). The Poisson regression estimating equations are
has received much attention recently (e.g. Traissac and others, 1999; McNutt and others, 2003; Zou, 2004; Carter and others, 2005). The Poisson regression estimating equations are 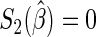 , where
, where
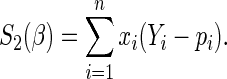 |
(2.5) |
It is apparent that the Poisson regression estimating equations are simply a special case of (2.3) with 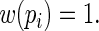 Thus, although the Poisson regression estimating equations produce consistent estimators of
Thus, although the Poisson regression estimating equations produce consistent estimators of 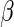 , they can be quite inefficient because
, they can be quite inefficient because 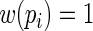 is not the optimal or asymptotically efficient weight function. In general, weight functions closer to
is not the optimal or asymptotically efficient weight function. In general, weight functions closer to 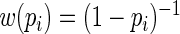 will have higher efficiency. Thus, the goal of this paper is to choose a
will have higher efficiency. Thus, the goal of this paper is to choose a 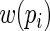 close to
close to 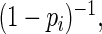 but one that also avoids the convergence problems associated with ML. Lumley and others (2006) considered the weights
but one that also avoids the convergence problems associated with ML. Lumley and others (2006) considered the weights 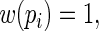
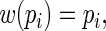 and
and 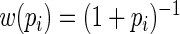 and estimated their relative efficiency (relative to the MLE). Lumley and others found that with
and estimated their relative efficiency (relative to the MLE). Lumley and others found that with 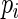 close to 1 these three estimating equations can give inefficient estimates; this is due to the fact that the three weight functions considered do not closely approximate the optimal weight function.
close to 1 these three estimating equations can give inefficient estimates; this is due to the fact that the three weight functions considered do not closely approximate the optimal weight function.
To develop more efficient estimating equations, we first note that the Maclaurin series (Abramowitz and Stegun, 1970) of 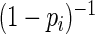 is
is
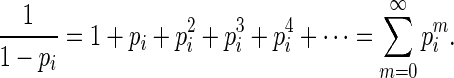 |
This series converges for 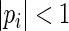 . For our proposed estimating equations for
. For our proposed estimating equations for 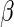 , we consider using weight functions of the form
, we consider using weight functions of the form
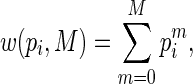 |
(2.6) |
for different finite values of 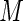 . Note that the Poisson regression estimating equations can be considered the Maclaurin series truncated at
. Note that the Poisson regression estimating equations can be considered the Maclaurin series truncated at 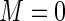 (i.e. constant weights). Higher values of
(i.e. constant weights). Higher values of 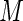 will more closely approximate the optimal weights associated with the MLE and should yield more efficient estimates.
will more closely approximate the optimal weights associated with the MLE and should yield more efficient estimates.
For any finite value of 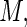 the proposed weight function can be implemented in standard statistical software for generalized linear models that allows user-defined variance functions (e.g. PROC GLIMMIX in SAS); there is negligible increase in computational time for larger values of
the proposed weight function can be implemented in standard statistical software for generalized linear models that allows user-defined variance functions (e.g. PROC GLIMMIX in SAS); there is negligible increase in computational time for larger values of 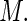 However, some care must be exercised in the choice of value for
However, some care must be exercised in the choice of value for 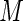 ; for very large values of
; for very large values of 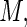
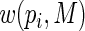 will be very close to
will be very close to 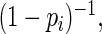 and the resulting estimating equations will be unstable when
and the resulting estimating equations will be unstable when 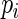 is close to 1. Recall that convergence problems with ML estimation arise when
is close to 1. Recall that convergence problems with ML estimation arise when 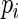 is close to 1 and the
is close to 1 and the 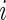 th observation receives excessively large weight in the estimating equations. We note here that, because
th observation receives excessively large weight in the estimating equations. We note here that, because 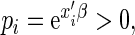
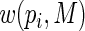 will always be positive. Also, for success probabilities close to 1 the weights are bounded, with largest
will always be positive. Also, for success probabilities close to 1 the weights are bounded, with largest 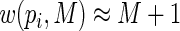 , so that convergence problems are less likely unless very large values of
, so that convergence problems are less likely unless very large values of 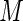 are chosen. In the next section, we examine the ARE for increasing number of terms (
are chosen. In the next section, we examine the ARE for increasing number of terms (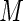 ) in the series and make recommendations for the choice of the number of terms to avoid similar finite sample convergence problems as with ML estimation. The challenge is to find some minimum value of
) in the series and make recommendations for the choice of the number of terms to avoid similar finite sample convergence problems as with ML estimation. The challenge is to find some minimum value of 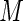 that provides near-optimal weights but essentially bounds the largest weights when
that provides near-optimal weights but essentially bounds the largest weights when 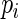 is close to 1.
is close to 1.
3. Asymptotic relative efficiency
The goal is to find a weight function that approximates the optimal weight function, 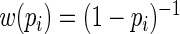 , but avoids assigning extremely large weights when
, but avoids assigning extremely large weights when 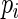 is close to 1. Using the truncated Maclaurin series of
is close to 1. Using the truncated Maclaurin series of 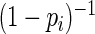 ,
, 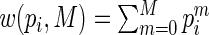 , we examine the ARE for increasing finite values of
, we examine the ARE for increasing finite values of 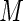 . For this study of ARE, we consider a log RR regression model with a single covariate,
. For this study of ARE, we consider a log RR regression model with a single covariate,
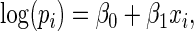 |
where, for simplicity, we let 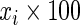 have a discrete uniform distribution on the set
have a discrete uniform distribution on the set 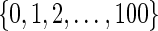 . We let
. We let 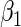 be negative, so that
be negative, so that 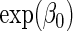 is the maximum value for any
is the maximum value for any 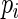 ; in contrast,
; in contrast, 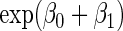 is the minimum value for any
is the minimum value for any 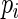 . For the study of ARE, we first specify the maximum,
. For the study of ARE, we first specify the maximum, 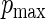 , and minimum,
, and minimum, 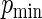 , values for
, values for 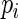 , which in turn fully specifies the parameters
, which in turn fully specifies the parameters 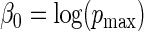 and
and 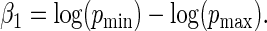 Specification of the model in this way allows us to explore properties of the estimators as
Specification of the model in this way allows us to explore properties of the estimators as 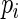 approaches 1. For different choices of values of
approaches 1. For different choices of values of 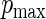 and
and 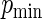 , we examine the ARE of the estimator of
, we examine the ARE of the estimator of 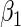 based on
based on 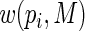 for increasing values of
for increasing values of 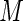 ranging from 0 to 100. Recall that, when
ranging from 0 to 100. Recall that, when 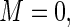 the weights are constant and equivalent to the Poisson regression estimator. Fixing
the weights are constant and equivalent to the Poisson regression estimator. Fixing  we let
we let 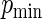 range from 0.2 to 0.8.
range from 0.2 to 0.8.
Given a discrete uniform distribution for 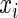 , and a Bernoulli distribution for
, and a Bernoulli distribution for 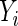 given
given 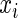 , the asymptotic variance of
, the asymptotic variance of 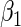 can be obtained from (2.4) by simply considering an artificial sample comprised of one properly weighted observation for each possible realization of (
can be obtained from (2.4) by simply considering an artificial sample comprised of one properly weighted observation for each possible realization of (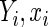 ). The weights are determined by the respective joint probabilities of the given realizations. Following Rotnitzky and Wypij (1994), the asymptotic variance of
). The weights are determined by the respective joint probabilities of the given realizations. Following Rotnitzky and Wypij (1994), the asymptotic variance of 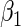 can be ascertained by weighting each contribution to
can be ascertained by weighting each contribution to 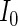 and
and 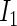 by its respective probability. That is, we take the expectations of
by its respective probability. That is, we take the expectations of 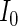 and
and 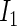 , the components of
, the components of 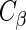 in (2.4), by summing all of the possible realizations weighted by their respective probabilities.
in (2.4), by summing all of the possible realizations weighted by their respective probabilities.
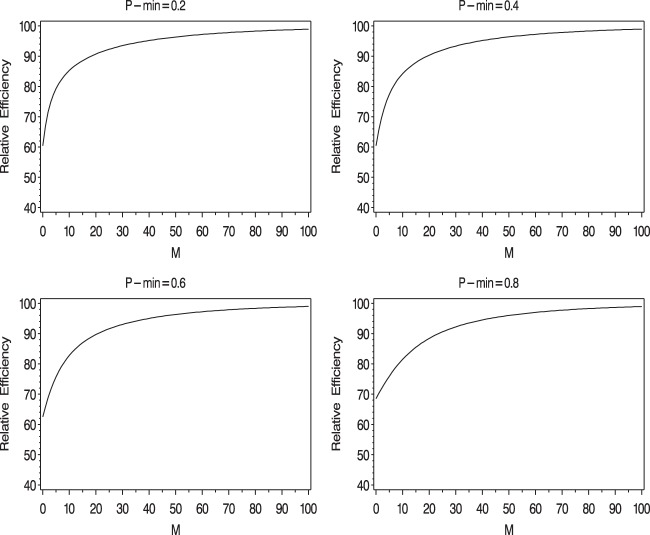
A plot of the ARE for increasing values of 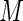 is given in Figure 1. The four panels of Figure 1 display the AREs for
is given in Figure 1. The four panels of Figure 1 display the AREs for 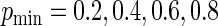 , respectively. As
, respectively. As 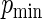 increases, the concentration of success probabilities that are close to 1 increases as the median of the probabilities increases from 0.44 when
increases, the concentration of success probabilities that are close to 1 increases as the median of the probabilities increases from 0.44 when 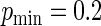 to 0.89 when
to 0.89 when 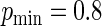 . In the four panels of Figure 1, the ARE for the Poisson regression estimator (
. In the four panels of Figure 1, the ARE for the Poisson regression estimator (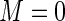 ) is in the 60–70% range. This highlights the loss of efficiency associated with the use of constant weights when the probabilities are not small. These results are in close agreement with those reported by Lumley and others (2006). As anticipated, the ARE increases monotonically with increasing values of
) is in the 60–70% range. This highlights the loss of efficiency associated with the use of constant weights when the probabilities are not small. These results are in close agreement with those reported by Lumley and others (2006). As anticipated, the ARE increases monotonically with increasing values of 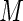 . AREs of approximately 95–97% are obtained for the proposed estimator when
. AREs of approximately 95–97% are obtained for the proposed estimator when 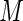 is between 40 and 60. We note that, for
is between 40 and 60. We note that, for 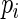 close to 1,
close to 1, 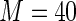 and
and 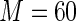 bound the maximum weights at approximately 41 and 61, respectively. For larger values of
bound the maximum weights at approximately 41 and 61, respectively. For larger values of 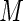 , there appears to be diminishing returns in terms of increases in efficiency. More importantly, however, larger values of
, there appears to be diminishing returns in terms of increases in efficiency. More importantly, however, larger values of 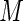 seem far more likely to produce problems with convergence in finite samples due to excessive weight assigned to observations with
seem far more likely to produce problems with convergence in finite samples due to excessive weight assigned to observations with 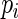 close to 1. In the next section, we examine the finite sample performance of the proposed estimator when
close to 1. In the next section, we examine the finite sample performance of the proposed estimator when 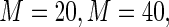 and
and 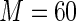 .
.
Fig. 1.
ARE for increasing number of terms (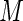 ) in Maclaurin series expansion of the optimal Bernoulli weight function.
) in Maclaurin series expansion of the optimal Bernoulli weight function.
4. Simulation study
In this section, we consider the finite sample properties of the proposed estimator. For the simulations, we used a similar configuration as in the study of ARE presented in Section 3:
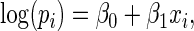 |
where, for simplicity, we let 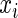 have a uniform (0,1) distribution. For the different values of
have a uniform (0,1) distribution. For the different values of 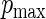 and
and 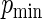 (or equivalently,
(or equivalently, 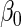 and
and 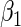 ), we conducted simulations for
), we conducted simulations for 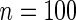 with 2500 simulation replications performed for each configuration. We performed simulations fixing
with 2500 simulation replications performed for each configuration. We performed simulations fixing  and letting
and letting 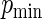 range from 0.2 to 0.8 in 0.2 unit increments. The simulations were used to compare the MLE (unconstrained), the Poisson regression estimator (
range from 0.2 to 0.8 in 0.2 unit increments. The simulations were used to compare the MLE (unconstrained), the Poisson regression estimator (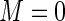 ), and the proposed estimator based on a Maclaurin series approximation with
), and the proposed estimator based on a Maclaurin series approximation with 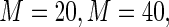 and
and 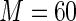 .
.
Table 2 presents the relative bias, defined as 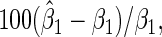 the root mean square error, the coverage probabilities of 95% Wald confidence intervals for
the root mean square error, the coverage probabilities of 95% Wald confidence intervals for 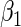 , as well as the percentage of simulation replications in which the convergence criterion was met. From Table 2, we see that the percent convergence for ML is less than
, as well as the percentage of simulation replications in which the convergence criterion was met. From Table 2, we see that the percent convergence for ML is less than 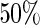 for all configurations; for ML, we report the results only for those simulations that converged for ML; the latter results can be considered “conditional on the likelihood convergence criterion”. In contrast, there were no convergence problems for any of the estimating equations approaches. In terms of bias, standard ML has non-negligible relative bias, and the relative bias increases as
for all configurations; for ML, we report the results only for those simulations that converged for ML; the latter results can be considered “conditional on the likelihood convergence criterion”. In contrast, there were no convergence problems for any of the estimating equations approaches. In terms of bias, standard ML has non-negligible relative bias, and the relative bias increases as 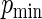 increases. The relative bias varies from approximately 8% to 30%. All other approaches have negligible (
increases. The relative bias varies from approximately 8% to 30%. All other approaches have negligible (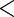 5%) relative biases. For the estimating equations approaches, the relative efficiencies can be estimated as the square of the ratio of the root mean square errors. The relative efficiencies of Poisson regression versus the Maclaurin series with
5%) relative biases. For the estimating equations approaches, the relative efficiencies can be estimated as the square of the ratio of the root mean square errors. The relative efficiencies of Poisson regression versus the Maclaurin series with 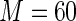 is between
is between 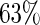 and
and 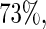 increasing from
increasing from 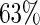 when
when 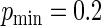 to
to 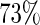 when
when 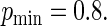 For these simulations, the relative efficiency of the Maclaurin series with
For these simulations, the relative efficiency of the Maclaurin series with 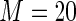 versus the Maclaurin series with
versus the Maclaurin series with 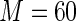 is above
is above 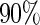 for all configurations (
for all configurations (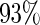 when
when 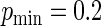 and
and 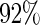 when
when  Also, the relative efficiency of the Maclaurin series with
Also, the relative efficiency of the Maclaurin series with 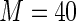 versus the Maclaurin series with
versus the Maclaurin series with 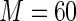 is approximately
is approximately 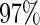 for all configurations. Interestingly, for these simulation configurations, even use of
for all configurations. Interestingly, for these simulation configurations, even use of 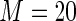 terms in the Maclaurin series yields high efficiency.
terms in the Maclaurin series yields high efficiency.
Table 2.
Simulation results for estimation of 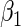 for
for 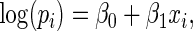
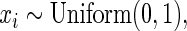 and
and 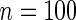
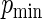 |
Method | Percent relative bias of 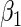
|
Root MSE | Coverage probability (%) | Percent converged (%) |
|---|---|---|---|---|---|
| 0.2 | Standard ML |
 7.51 7.51 |
3.103 | 95.6 | 47.9 |
| Poisson | 2.64 | 3.767 | 95.8 | 100.0 | |
MS (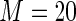 ) ) |
0.97 | 3.097 | 95.7 | 100.0 | |
MS (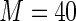 ) ) |
0.50 | 3.019 | 96.1 | 100.0 | |
MS (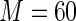 ) ) |
0.21 | 2.985 | 96.0 | 100.0 | |
| 0.4 | Standard ML |
 12.02 12.02 |
2.278 | 94.0 | 48.2 |
| Poisson | 1.60 | 2.657 | 94.5 | 100.0 | |
MS (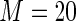 ) ) |
 0.45 0.45 |
2.183 | 94.2 | 100.0 | |
MS (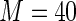 ) ) |
 0.97 0.97 |
2.131 | 94.4 | 100.0 | |
MS (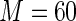 ) ) |
 1.33 1.33 |
2.106 | 94.3 | 100.0 | |
| 0.6 | Standard ML |
 17.53 17.53 |
1.668 | 93.3 | 48.0 |
| Poisson | 0.81 | 1.877 | 95.0 | 100.0 | |
MS (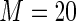 ) ) |
 1.50 1.50 |
1.553 | 95.3 | 100.0 | |
MS (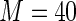 ) ) |
 2.10 2.10 |
1.505 | 95.0 | 100.0 | |
MS (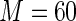 ) ) |
 2.51 2.51 |
1.482 | 94.9 | 100.0 | |
| 0.8 | Standard ML |
 31.42 31.42 |
1.153 | 90.5 | 46.7 |
| Poisson | 1.22 | 1.244 | 93.6 | 100.0 | |
MS (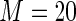 ) ) |
 2.07 2.07 |
1.109 | 93.2 | 100.0 | |
MS (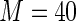 ) ) |
 3.02 3.02 |
1.078 | 93.2 | 100.0 | |
MS (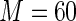 ) ) |
 3.65 3.65 |
1.063 | 93.2 | 100.0 |
5. Application to study of pre-operative use of beta blockers in patients with colon cancer
We apply the proposed methodology to the analysis of pre-operative use of beta blockers (yes/no) among patient undergoing colorectal surgery after diagnosis of colon cancer (Arriaga and others, 2009). To examine the relationship between the binary outcome and the five patient-level predictors of interest, we fit the following RR regression model:
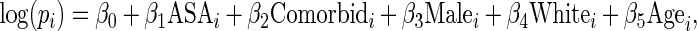 |
(5.1) |
where 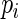 is the conditional probability that the
is the conditional probability that the 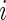 th patient receives pre-operative beta blockers;
th patient receives pre-operative beta blockers; 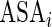 is 1 if life-threatening disease and 0 otherwise;
is 1 if life-threatening disease and 0 otherwise; 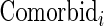 is the number of comorbidities;
is the number of comorbidities; 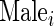 is 1 if male and 0 if female;
is 1 if male and 0 if female; 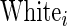 is 1 if White race and 0 if otherwise; and
is 1 if White race and 0 if otherwise; and 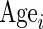 is age in years (although the reported effect of age is multiplied by 10 for easier comparison of results in Table 3).
is age in years (although the reported effect of age is multiplied by 10 for easier comparison of results in Table 3).
Table 3.
Comparison of (log) RR regression estimates for the probability of pre-operative use of beta blockers among patients undergoing colorectal surgery
| Effect | Approach | Estimate | SE | 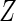 |
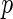 -value -value |
|---|---|---|---|---|---|
| Intercept | Standard ML |
 1.186 1.186 |
0.310 |
 3.82 3.82 |
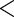 0.001 0.001 |
| Poisson |
 1.542 1.542 |
0.321 |
 4.81 4.81 |
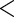 0.001 0.001 |
|
MS (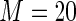 ) ) |
 1.445 1.445 |
0.262 |
 5.51 5.51 |
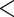 0.001 0.001 |
|
MS (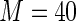 ) ) |
 1.445 1.445 |
0.253 |
 5.71 5.71 |
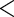 0.001 0.001 |
|
MS (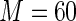 ) ) |
 1.439 1.439 |
0.251 |
 5.73 5.73 |
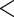 0.001 0.001 |
|
| ASA | Standard ML |
 0.009 0.009 |
0.097 |
 0.10 0.10 |
0.923 |
| Poisson |
 0.017 0.017 |
0.119 |
 0.15 0.15 |
0.884 | |
MS (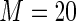 ) ) |
 0.007 0.007 |
0.116 |
 0.06 0.06 |
0.950 | |
MS (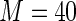 ) ) |
 0.007 0.007 |
0.114 |
 0.07 0.07 |
0.948 | |
MS (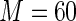 ) ) |
 0.008 0.008 |
0.114 |
 0.07 0.07 |
0.946 | |
| Comorbid | Standard ML | 0.065 | 0.044 | 1.46 | 0.145 |
| Poisson | 0.080 | 0.040 | 2.00 | 0.047 | |
MS (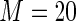 ) ) |
0.078 | 0.030 | 2.60 | 0.010 | |
MS (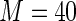 ) ) |
0.076 | 0.028 | 2.74 | 0.007 | |
MS (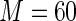 ) ) |
0.074 | 0.027 | 2.77 | 0.006 | |
| Male | Standard ML |
 0.068 0.068 |
0.098 |
 0.69 0.69 |
0.488 |
| Poisson |
 0.120 0.120 |
0.107 |
 1.11 1.11 |
0.266 | |
MS (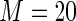 ) ) |
 0.053 0.053 |
0.088 |
 0.60 0.60 |
0.552 | |
MS (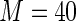 ) ) |
 0.048 0.048 |
0.080 |
 0.60 0.60 |
0.551 | |
MS (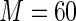 ) ) |
 0.047 0.047 |
0.076 |
 0.61 0.61 |
0.541 | |
| White | Standard ML |
 0.105 0.105 |
0.131 |
 0.80 0.80 |
0.422 |
| Poisson |
 0.157 0.157 |
0.152 |
 1.03 1.03 |
0.303 | |
MS (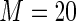 ) ) |
 0.139 0.139 |
0.148 |
 0.94 0.94 |
0.349 | |
MS (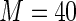 ) ) |
 0.138 0.138 |
0.148 |
 0.93 0.93 |
0.351 | |
MS (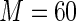 ) ) |
 0.138 0.138 |
0.148 |
 0.93 0.93 |
0.352 | |
| Age | Standard ML | 0.111 | 0.044 | 2.52 | 0.013 |
| Poisson | 0.160 | 0.047 | 3.41 | 0.001 | |
MS (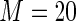 ) ) |
0.139 | 0.037 | 3.76 |
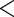 0.001 0.001 |
|
MS (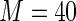 ) ) |
0.139 | 0.034 | 4.08 |
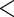 0.001 0.001 |
|
MS (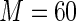 ) ) |
0.139 | 0.033 | 4.18 |
 0.001 0.001 |
Table 3 presents the estimates of 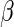 obtained using standard ML (as implemented in SAS PROC GENMOD), the Poisson quasi-likelihood approach (McNutt and others, 2003; Zou, 2004; Carter and others, 2005), and the Maclaurin series approach with
obtained using standard ML (as implemented in SAS PROC GENMOD), the Poisson quasi-likelihood approach (McNutt and others, 2003; Zou, 2004; Carter and others, 2005), and the Maclaurin series approach with 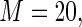
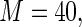 and
and  Of note, there were convergence problems with ML but not with any of the other approaches. In particular, for ML SAS PROC GENMOD produced a warning message that “The relative Hessian convergence criterion of 0.0198000361 is greater than the limit of 0.0001. The convergence is questionable”.
Of note, there were convergence problems with ML but not with any of the other approaches. In particular, for ML SAS PROC GENMOD produced a warning message that “The relative Hessian convergence criterion of 0.0198000361 is greater than the limit of 0.0001. The convergence is questionable”.
As conjectured by the study investigators, the results in Table 3 indicate that older patients and patients with more comorbidities are significantly more likely to receive pre-operative beta blockers. From the results presented in Table 3, it is also apparent that the quantitative variable age and the ordinal variable “number of comorbidities” show the largest estimated efficiency gains when comparing the Poisson (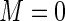 ) to the Maclaurin series estimators. The relative efficiencies can be estimated as the square of the ratio of the estimated standard errors. For the covariate “number of comorbidities”, the estimated relative efficiency of Poisson regression versus the Maclaurin series with
) to the Maclaurin series estimators. The relative efficiencies can be estimated as the square of the ratio of the estimated standard errors. For the covariate “number of comorbidities”, the estimated relative efficiency of Poisson regression versus the Maclaurin series with 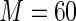 is approximately
is approximately 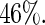 For the covariate age, the estimated relative efficiency of Poisson regression versus the Maclaurin series with
For the covariate age, the estimated relative efficiency of Poisson regression versus the Maclaurin series with 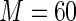 is approximately
is approximately 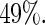 Thus, in this particular application, Poisson regression appears to be quite inefficient compared with the proposed Maclaurin series approach.
Thus, in this particular application, Poisson regression appears to be quite inefficient compared with the proposed Maclaurin series approach.
For the covariate “number of comorbidities”, the estimated relative efficiency of Maclaurin series with 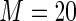 versus the Maclaurin series with
versus the Maclaurin series with 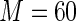 is greater than
is greater than 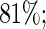 similarly, for the covariate age, it is above
similarly, for the covariate age, it is above 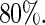 Thus, in this applications, there appears to be discernible gains from using a Maclaurin series with
Thus, in this applications, there appears to be discernible gains from using a Maclaurin series with 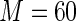 instead of
instead of  However, there is no appreciable difference between Maclaurin series with
However, there is no appreciable difference between Maclaurin series with 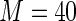 and
and  This reinforces the results from Sections 3 and 4 where it was found that there are diminishing returns in terms of increases in efficiency when
This reinforces the results from Sections 3 and 4 where it was found that there are diminishing returns in terms of increases in efficiency when 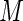 is greater than 40–60.
is greater than 40–60.
6. Conclusion
To circumvent the usual convergence problems associated with the ML estimator, we propose estimators that approximate the optimal weight function based on the truncated Maclaurin series of 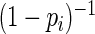 . This use of a near-optimal weight function that bounds the largest weights yields estimators with relatively high efficiency that also avoid convergence problems. In our study of asymptotic efficiency, the proposed estimator with weight function based on 40–60 terms from the Maclaurin series was 95–97% efficient relative to the MLE. This compares favorably to the Poisson regression estimator that was found to be only 60–70% efficient. In simulations with samples of size 50 (data not shown) and 100, we found similar gains in relative efficiency and no convergence problems with the proposed estimator based on 40–60 terms. In addition, the proposed estimator, using any finite number of terms, is straightforward to implement in standard statistical software for generalized linear models that allows user-defined variance functions (e.g. PROC GLIMMIX in SAS). Finally, we note that estimators that approximate the optimal weight function based on truncated series expansions may also be useful for other generalized linear models in which the link function does not respect the natural parameter constraints (e.g. linear or linear-expit models for binary data (Kovalchik and others, 2013)).
. This use of a near-optimal weight function that bounds the largest weights yields estimators with relatively high efficiency that also avoid convergence problems. In our study of asymptotic efficiency, the proposed estimator with weight function based on 40–60 terms from the Maclaurin series was 95–97% efficient relative to the MLE. This compares favorably to the Poisson regression estimator that was found to be only 60–70% efficient. In simulations with samples of size 50 (data not shown) and 100, we found similar gains in relative efficiency and no convergence problems with the proposed estimator based on 40–60 terms. In addition, the proposed estimator, using any finite number of terms, is straightforward to implement in standard statistical software for generalized linear models that allows user-defined variance functions (e.g. PROC GLIMMIX in SAS). Finally, we note that estimators that approximate the optimal weight function based on truncated series expansions may also be useful for other generalized linear models in which the link function does not respect the natural parameter constraints (e.g. linear or linear-expit models for binary data (Kovalchik and others, 2013)).
In general, RR regression is most useful when the scientific goal is to estimate the association between an exposure or intervention and a commonly occurring binary outcome, with appropriate adjustment for additional covariates. However, we note that although the estimating equations (2.3) yield consistent estimators of 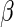 for any choice of weight function, including the optimal weight function and the approximation to it proposed in this paper, the estimators are not constrained to produce estimated
for any choice of weight function, including the optimal weight function and the approximation to it proposed in this paper, the estimators are not constrained to produce estimated 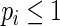 . As a result, RR regression should be avoided altogether when the scientific goal is to make predictions; when the goal is prediction, models where the constraints on the probabilities are automatically satisfied (e.g. logistic regression) should be adopted instead.
. As a result, RR regression should be avoided altogether when the scientific goal is to make predictions; when the goal is prediction, models where the constraints on the probabilities are automatically satisfied (e.g. logistic regression) should be adopted instead.
Funding
We are grateful for the support provided by grants MH054693 and CA160679 from the United States National Institutes of Health (NIH).
Acknowledgements
Conflict of Interest: None declared.
References
- Abramowitz M., Stegun I. A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover Publications; 1970. 9th printing. [Google Scholar]
- Arriaga A. F., Lancaster R. T., Berry W. R., Regenbogen S. E., Lipsitz S. R., Kaafarani H. M., Elbardissi A. W., Desai P., Ferzoco S. J., Bleday R., others The better colectomy project: association of evidence-based best-practice adherence rates to outcomes in colorectal surgery. Annals of Surgery. 2009;250:507–513. doi: 10.1097/SLA.0b013e3181b672bc. [DOI] [PubMed] [Google Scholar]
- Baumgarten M., Seliske P., Goldberg M. S. Warning regarding the use of GLIM macros for the estimation of risk ratios. American Journal of Epidemiology. 1989;130:1065. doi: 10.1093/oxfordjournals.aje.a115407. [DOI] [PubMed] [Google Scholar]
- Carter R. E., Lipsitz S. R., Tilley B. C. Quasi-likelihood estimation for relative risk regression models. Biostatistics. 2005;6:39–44. doi: 10.1093/biostatistics/kxh016. [DOI] [PubMed] [Google Scholar]
- Clogg C. C., Rubin D. B., Schenker N., Schultz B., Weidman L. Multiple imputation of industry and occupation codes in census public-use samples using Bayesian logistic regression. Journal of the American Statistical Association. 1991;86:68–78. [Google Scholar]
- Deddens J. A., Petersen M. R., Lei X. Proceeding of the 28th Annual SAS Users Group International Conference. Cary, NC: SAS Institute Inc.; 2003. Estimation of prevalence ratios when PROC GENMOD does not converge; pp. 270–278. [Google Scholar]
- Huber P. J. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Berkeley: University of California Press; 1967. The behavior of maximum likelihood estimates under nonstandard conditions; pp. 221–233. Volume 1. [Google Scholar]
- Jewell N. P. Statistics for Epidemiology. New York: Chapman & Hall/CRC Press; 2003. [Google Scholar]
- Kovalchik S. A., Varadhan R., Fetterman B., Poitras N. E., Wacholder S., Katki H. A. A general binomial regression model to estimate standardized risk differences from binary response data. Statistics in Medicine. 2013;32:808–821. doi: 10.1002/sim.5553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu M., Tilley B. C. Use of odds ratio or relative risk to measure a treatment effect in clinical trials with multiple correlated binary outcomes: data from the NINDS t-PA stroke trial. Statistics in Medicine. 2001;20:1891–1901. doi: 10.1002/sim.841. [DOI] [PubMed] [Google Scholar]
- Lumley T., Kronmal R., Ma S. Relative risk regression in medical research: models, contrasts, estimators, and algorithms. UW Biostatistics Working Paper Series. 2006 Working Paper 293. http://biostats.bepress.com/uwbiostat/paper293 . [Google Scholar]
- McNutt L. A., Wu C., Xue X., Hafner J. P. Estimating relative risk in cohort studies and clinical trials of common events. American Journal of Epidemiology. 2003;157:940–943. doi: 10.1093/aje/kwg074. [DOI] [PubMed] [Google Scholar]
- Owens W. D., Felts J. A., Spitznagel E. L., Jr ASA physical status classifications: a study of consistency of ratings. Anesthesiology. 1978;49:239–243. doi: 10.1097/00000542-197810000-00003. [DOI] [PubMed] [Google Scholar]
- Poldermans D., Boersma E., Bax J. J., Thomson I. R., van de Ven L. L., Blankensteijn J. D., Baars H. F., Yo T. I., Trocino G., Vigna C., Roelandt J. R., van Urk H. The effect of bisoprolol on perioperative mortality and myocardial infarction in high-risk patients undergoing vascular surgery. The New England Journal of Medicine. 1999;341:1789–1794. doi: 10.1056/NEJM199912093412402. [DOI] [PubMed] [Google Scholar]
- Rotnitzky A. Inverse probability weighted methods. In: Fitzmaurice G., Davidian M., Verbeke G., Molenberghs G., editors. Longitudinal Data Analysis. Boca Raton: Chapman & Hall/CRC Press; 2009. pp. 453–476. [Google Scholar]
- Rotnitzky A., Wypij D. A note on the bias of estimators with missing data. Biometrics. 1994;50:1163–1170. [PubMed] [Google Scholar]
- Royall R. M. Model robust confidence intervals using maximum likelihood estimators. International Statistical Review. 1986;54:221–226. [Google Scholar]
- Traissac P., Martin-Prevel Y., Delpeuch F., Maire B. Regression logistique vs autres modeles lineaires generalises pour l'estimation de rapports de prevalences. Rev Epidemiol Sante Publique. 1999;47:593–604. [PubMed] [Google Scholar]
- Wacholder S. Binomial regression in GLIM: estimating risk ratios and risk differences. American Journal of Epidemiology. 1986;123:174–184. doi: 10.1093/oxfordjournals.aje.a114212. [DOI] [PubMed] [Google Scholar]
- Wedderburn R. W. M. Quasi-likelihood functions, generalized linear models, and the gauss newton method. Biometrika. 1974;61:439–447. [Google Scholar]
- White H. Maximum likelihood estimation under mis-specified models. Econometrica. 1982;50:1–26. [Google Scholar]
- Zhang J., Yu K. F. What's the relative risk?: a method of correcting the odds ratio in cohort studies of common outcomes. Journal of the American Medical Association. 1998;280:1690–1691. doi: 10.1001/jama.280.19.1690. [DOI] [PubMed] [Google Scholar]
- Zou G. A modified Poisson regression approach to prospective studies with binary data. American Journal of Epidemiology. 2004;159:702–706. doi: 10.1093/aje/kwh090. [DOI] [PubMed] [Google Scholar]