Measured long-range repulsive Casimir–Lifshitz forces

Abstract

Quantum fluctuations create intermolecular forces that pervade macroscopic bodies^1–3. At molecular separations of a few nanometres or less, these interactions are the familiar van der Waals forces⁴. However, as recognized in the theories of Casimir, Polder and Lifshitz^5–7, at larger distances and between macroscopic condensed media they reveal retardation effects associated with the finite speed of light. Although these long-range forces exist within all matter, only attractive interactions have so far been measured between material bodies^8–11. Here we show experimentally that, in accord with theoretical prediction¹², the sign of the force can be changed from attractive to repulsive by suitable choice of interacting materials immersed in a fluid. The measured repulsive interaction is found to be weaker than the attractive. However, in both cases the magnitude of the force increases with decreasing surface separation. Repulsive Casimir–Lifshitz forces could allow quantum levitation of objects in a fluid and lead to a new class of switchable nanoscale devices with ultra-low static friction^13–15.

The van der Waals force between molecules⁴ or, more generally, small dielectric particles¹⁶, results in large part from their quantum mechanical zero-point energy, which induces electromagnetic charge fluctuations that interact at small separations. At larger distances, typically more than a few nanometres, a qualitatively new regime is entered: the interaction is no longer instantaneous owing to the finite speed of light. As first shown by Casimir and Polder⁶, this ‘retardation effect’ causes the force to fall more rapidly with distance than in the short-range van der Waals limit.

Interactions due to quantum fluctuations impinge on fields ranging from fundamental physics to chemistry and biology when surfaces are in contact or in close proximity². Their consequences are felt in phenomena such as adhesion, friction, wetting and stiction^2,17. Casimir's formulation for the interaction between ideal metals in vacuum was extended by Lifshitz, Dzyaloshinskii and Pitaevskii to macroscopic bodies made of real materials described by their dielectric response functions. Their formulation included solids or liquids separated by a fluid^7,12. As between two molecules, one can distinguish a short-range van der Waals regime and a retarded long-range regime characterized by a stronger dependence on separation. Several measurements have confirmed the theoretically predicted attractive forces between electrically neutral surfaces^8,9.

Recently there has been renewed interest in measuring the Casimir–Lifshitz force with higher precision and in applying it to the design of nanomechanical devices^10,18–20. So far, however, all measurements of Casimir–Lifshitz forces have revealed attractive interactions. Although repulsive forces have been predicted¹², no direct measurement of long-range repulsion between material bodies has (to our knowledge) been reported. In the non-retarded van der Waals limit (surface separations up to a few nanometres), evidence for repulsive interactions between solids separated by a liquid has been presented^15,21–24. When working at small separations, however, the polarity and orientation of the molecules may influence the force. Measurements at larger separations do not suffer from this problem because solvation forces die out with characteristic decay lengths the size of solvent molecules. Note also that the long-range repulsion addressed here is different from the prediction of a repulsive force associated with the geometry of the boundary conditions, which has been criticized in the literature (see ref. 25 and references therein), or with the use of metamaterials²⁶.

In this Letter, we report the direct measurement of long-range repulsive forces between solids separated by a fluid. We compare the results with Lifshitz's theory and find them to be consistent within the uncertainties of the optical properties of the materials.

Repulsive forces between macroscopic bodies can be qualitatively understood by considering their material polarizabilities or, better, their dielectric response functions: ε₁, ε₂ and ε₃ (see Supplementary Information). The interaction of material 1 with material 2 across medium 3 goes as a summation of terms with differences in material permittivities

$$-({\mathit{\varepsilon }}_1-{\mathit{\varepsilon }}_3)({\mathit{\varepsilon }}_2-{\mathit{\varepsilon }}_3)$$ (1)

over frequencies ξ that span the entire spectrum^2,12. Between two like materials, ε₁ = ε₂, these terms are negative and correspond to attraction. However, when the dielectric response ε₃ of the medium is between ε₁ and ε₂,

$${\mathit{\varepsilon }}_1>{\mathit{\varepsilon }}_3>{\mathit{\varepsilon }}_2$$ (2)

then the −(ε₁ − ε₃) (ε₂ − ε₃) terms are positive; the force is repulsive.

An easy-to-see limit for this repulsion is the case where region 2 is air or vacuum and the polarizability of medium 3 is less than that of substrate 1 (see, for example, ref. 2, pages 27 and 58). As a result, substance 3, rather than form a droplet, spreads out to achieve maximum proximity to substance 1.

Examples of material systems that obey equation (2) are rare but do exist. One of the earliest successes of Lifshitz's equation was the quantitative explanation of the thickening of a superfluid helium film on the walls of a container^12,27. In that system, it is energetically more favourable for the liquid to be between the vapour and the container, and the liquid climbs the wall. One set of materials (solid–liquid– solid) that obeys inequality (2) over a large frequency range is gold, bromobenzene and silica (Fig. 1b; see also Supplementary Information for a discussion of the optical properties).

Figure 1. Repulsive quantum electrodynamical forces can exist for two materials separated by a fluid.

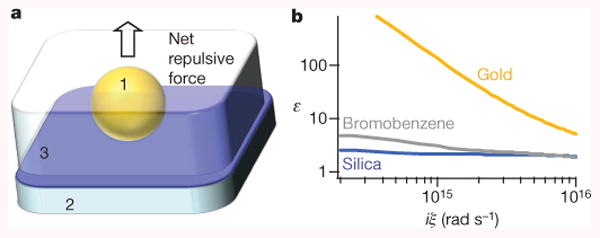
a, The interaction between material 1 and material 2 immersed in a fluid (material 3) is repulsive when ε₁(iξ) > ε₃(iξ) > ε₂(iξ), where the ε(iξ) terms are the dielectric functions at imaginary frequency (see Supplementary Information for details about the definition of ε(iξ)). b, The optical properties of gold, bromobenzene and silica are such that ε_gold(iξ) > ε_bromobenzene(iξ) > ε_silica(iξ) and lead to a repulsive force between the gold and silica surfaces.

Our measurements are conducted between a large plate and a 39.8 μm diameter polystyrene sphere coated with a 100 nm thick gold film, which is attached to a cantilever and mounted on an atomic force microscope with a fluid-filled cell (Fig. 2a). Light from a superluminescent diode is reflected off the back of the cantilever and is used to monitor its bending. To advance the sphere towards the plate, an Asylum Research linear variable differential transformer is used to control a piezo column, which reduces hysteresis and nonlinearities inherent in piezoelectrics. Any interaction between the sphere and the plate will result in a bending of the cantilever and a change in the detector signal that monitors the difference in light intensity between the top half of the detector and the bottom half of the detector. This difference signal is proportional to the force.

Figure 2. Experimental set-up and deflection data.

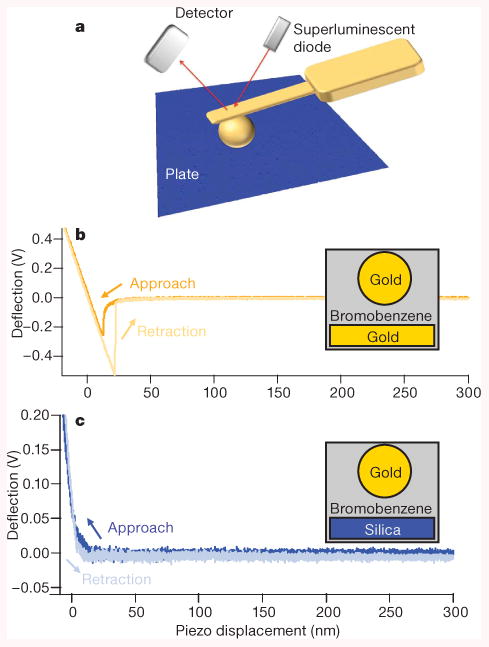
a, A sphere is attached to an atomic force microscope cantilever, which is enclosed within a bromobenzene-filled cell for force measurements. b, Deflection data showing attractive interactions between a gold sphere and a gold plate. c, For the case of the same gold sphere and a silica plate, deflection data show a repulsive interaction evident during both approach and retraction. Note that the deflection voltage signal is a difference signal obtained from the detector and is proportional to the bending of the cantilever, as discussed in the text.

Cleaning procedures are performed on all surfaces before measurements. The silica plate, gold plate (consisting of a silica plate coated with 200 nm of gold) and fluid cell are ultrasonically cleaned for 30 min in ethanol followed by drying in flowing nitrogen. The cantilever chip is similarly rinsed with ethanol, but without ultrasonic cleaning (to avoid damage).

Electrostatic force microscopy is performed on the samples to ensure that surface charge effects are small and will not mask the Casimir–Lifshitz force (see Supplementary Information). For both the silica and gold plates used in the experiments, no evidence of excess charge accumulation is found. Similarly, no electrostatic double-layer force is expected for clean, uncharged surfaces separated by a fluid of low dielectric constant like bromobenzene¹⁷.

Force measurements are conducted in a fluid-filled cell containing both the gold and silica plates. The cantilever is completely submerged in bromobenzene (EM Science, Merck), which is filtered through a 0.2 μm PTFE filter before use. The set-up is assembled and allowed to equilibrate for 1 h before measurements. All measurements are performed at room temperature.

Raw deflection versus piezo displacement data show that the force is changed from attractive to repulsive by replacing the gold plate with the silica plate (Fig. 2b, c). The data in Fig. 2b, c were acquired with a piezo speed of 45 nm s^–1. With the gold plate, the cantilever is bent towards the surface during the approach, which corresponds to an attractive force between the sphere and plate until contact (Fig. 2b). Once contact is made, the normal force of the plate pushes against the sphere. Upon retraction, the sphere sticks to the plate for an additional 10 nm, owing to stiction between the two gold surfaces, before losing contact with the surface. When the silica plate is used, the cantilever is bent away from the surface during the approach, corresponding to a repulsive interaction (Fig. 2c). During retraction, the sphere continues to show repulsion. This cannot be a result of the hydrodynamic force, because that force is in a direction that opposes the motion of the sphere and will change sign as the direction is changed. Similarly, the repulsion observed in Fig. 2c cannot be due to charge trapped on silica; any charge that does exist on the surface will induce an image charge of opposite sign on the metal sphere and lead to an attractive interaction.

The detector signal is converted to a force signal by calibration with the hydrodynamic force²⁸. By performing measurements at different piezo speeds, we can isolate the hydrodynamic force from the Casimir–Lifshitz force for calibration purposes²⁸. Because the hydrodynamic force is linear with velocity, subtracting the total measured force at two different speeds results in only a hydrodynamic force with no contribution from the Casimir–Lifshitz force. A similar scheme can be used to distinguish the Casimir–Lifshitz force. Experimental precautions to minimize electrostatic effects are described in detail in the Supplementary Information and in ref. 28.

The measured forces after calibration show a clear distinction between the attractive and repulsive regimes when the plateis changed from gold to silica (Fig. 3a). The blue (orange) circles correspond to the average force from 50 runs between the gold sphere and the silica (gold) plate. Histograms of the force data at different distances show a Gaussian distribution and no evidence of systematic errors (see Supplementary Information). For clarity, error bars, which represent the standard deviation of the data, are shown for only seven points.

Figure 3. Attractive and repulsive Casimir–Lifshitz force measurements.

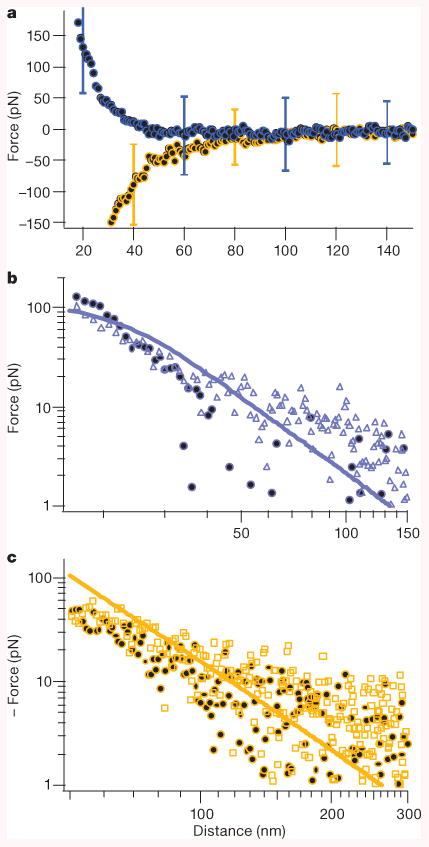
a, Blue (orange) circles represent the average of 50 data sets for the force between a gold sphere and a silica (gold) plate in bromobenzene. For clarity, error bars, which represent the standard deviation of the data, are only shown for seven data points. b, Measured repulsive force betweena gold sphere and a silica plate in bromobenzene on a log–log scale (blue circles) and calculated force using Lifshitz's theory (solid line) including corrections for the measured surface roughness of the sphere and the plate. Blue triangles are force data for another gold sphere (nominally of the same diameter)/silica plate pair. c, Measured attractive force on a log–log scale for two gold sphere/plate pairs (circles and squares) in bromobenzene. The calculated force includes surface roughness corrections corresponding tothe data represented by the circles (see Supplementary Information for calculations).

The experiment is repeated with an additional sphere and plate for both configurations. Figure 3b shows the measured force for two different spheres of nominally the same diameter and two different silica plates. Similar measurements for two spheres and gold plates are shown in Fig. 3c. The solid lines are the temperature dependent Lifshitz's theory including surface roughness corrections (see Supplementary Information) for the first sphere–plate pair (circles). Because the second set of measurements are made with spheres and plates of similar surface roughness and size, the corrections are of similar magnitude.

Uncertainties in the optical properties of the materials used are probably responsible for the significant discrepancy between theory and experiment. Previous measurements of attractive forces between gold surfaces in ethanol^11,28 showed a smaller discrepancy between theory and experiments. This comparison leads us to believe that the two-oscillator model (see Supplementary Information) is insufficient for detailed theoretical analysis using bromobenzene. Besides, measurements of the optical properties over a large spectral range are not available for bromobenzene. It is also possible that the optical properties are modified for very thin films. In addition to the uncertainties in the optical properties of the materials, discrepancies between theory and experiment are expected at small separations. There the surface roughness correction to Lifshitz's theory begins to fail when the surface roughness is of comparable size to the surface separation. Finally, we note that for the largest distances shown in Fig. 3b, c the averaged values for the force magnitude appear to be greater than the predicted value of the force from Lifshitz's theory. However, it should be stressed that this appearance is mostly due to logarithmic compression of the vertical axis and the fact that negative values are necessarily omitted on the log–log plot. It should further be noted that force magnitudes below 10pN cannot be accurately determined because of the relatively large spread in the data.

Finally, other effects are sometimes named after Casimir, which are not quantum electrodynamic in origin but rather the result of thermodynamic fluctuations. The critical Casimir effect is one such phenomenon (see, for example, ref. 29 and references therein); however, this effect is not present in our experiment because it occurs only in binary liquid mixtures near a critical point. Away from the critical point, the correlation length is too small to result in a force between macroscopic surfaces separated by tens or hundreds of nanometres. Thermal acoustic pressure fluctuations can also occur between two surfaces separated by a third material and give rise to an attractive force sometimes referred to as the acoustic Casimir effect³⁰. For two plates that are perfect reflectors of electromagnetic and acoustic waves, the ratio of the acoustic Casimir force to the quantum electrodynamic Casimir force is about 0.06 at 100 nm and room temperature³⁰. The introduction of a fluid results in a decrease of the acoustic impedance mismatch, and hence a reduction in the acoustic Casimir force due to a weaker confinement of pressure fluctuations. Given these results, we expect the acoustic Casimir effect to be similarly small for our system.

We have presented detailed measurements, which unambiguously show that long-range quantum electrodynamic forces between solid bodies can become repulsive when the optical properties of the materials are properly chosen. With such materials, quantum levitation of one surface above another in a fluid should be possible and could lead to the suppression of stiction and to ultra-low friction devices and sensors^13–15.