Fig. 1.
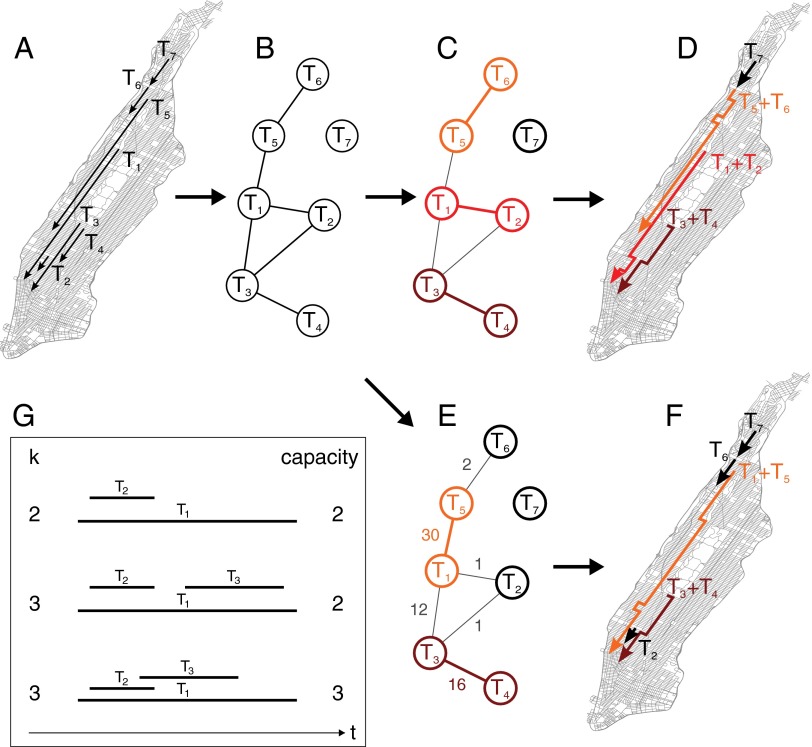
Shareability networks translate spatiotemporal sharing problems into a graph-theoretic framework that provides efficient solutions. (A) Example of seven trips, T1,…, T7, requested and to be shared in Manhattan, New York City. (B) Construction of shareability network for k = 2. Trips that could potentially be shared are connected, given the necessary time constraints to hold which we assume here to be the case. Trips 1 and 4 cannot be shared because the total length of the best shared route would be longer than the sum of the single routes. Likewise, trip 7 is an isolated node because it cannot possibly be shared with other trips. (C) Maximum matching of the shareability network gives the maximum number of trip pairs, i.e., the maximum number of shared trips. (D) Implementation (routing) of the maximum matching solution. (E) Alternatively, maximum weighted matching of the shareability network gives the solution with the minimal total travel time, which in this case leads to a different solution than unweighted maximum matching. Here only two pairs of trips are shared, but the amount of travel time saved, given by the sum of link weights of the matching, 30 + 16, is optimal. (F) Implementation (routing) of the weighted maximum matching solution. (G) k sharing and taxi capacity. Each of the three cases involves a number of trips Ti to be shared, but ordered differently in time t. (Top) This case corresponds to a feasible sharing according to our model with k = 2, and the trips can be accommodated in a taxi with capacity ≥2. (Middle) This case corresponds to a model with k = 3 because three trips are combined, but the three trips can be combined in a taxi with capacity = 2 because two of the trips are nonoverlapping. (Bottom) This case corresponds to k = 3, but here a taxi capacity ≥3 is needed to accommodate the combined trips. Here we are assuming one passenger per trip, in line with the data reported in ref. 18, according to which the average number of passengers per trip is 1.3.