Fig. 3.

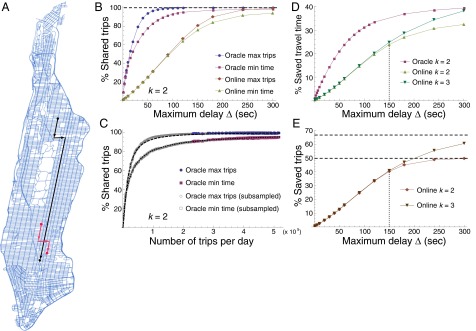
Benefits of trip sharing. (A) Street network of Manhattan, and examples of two trips that can be shared under the omniscient Oracle model, but not under the Online model. The starting time of the red trip is much later than that of the black trip, but in the Online model trip sharing decisions must be taken within a very short time window δ = 1 min to notify customers of trip-sharing opportunities as soon as possible after their order. (B) Percentage of shared trips as a function of the trip time delay Δ in the Oracle and in the Online model for the two considered optimization criteria of maximizing shared trips (max trips) and minimizing total travel time (min time), when up to k = 2 trips can be shared. (C) Shareability as a function of trips per day in the Oracle model. Typical days in New York City feature around 400,000 trips with near-maximum shareability. Subsampling data by randomly removing vehicles reveals the underlying saturation curves, fit (dashed lines) by a simple function of type $f\left(x\right)=K{x}^n/\left(1+K{x}^n\right)$ with the two parameters K and n well-known in adsorption processes and biochemical systems (SI Appendix). The fast, hyperbolic saturation implies that taxi sharing could be effective even in cities with vehicle densities much lower than New York, or when the willingness to share is low. (D) Percentage of saved travel time as a function of Δ for k = 2 and k = 3. Although δ is reduced from practically infinite in the Oracle model to δ = 1 min in the Online model, saved travel time is well above 30% for Δ = 300 s, for k = 3 almost reaching the maximum possible value from the Oracle model with k = 2. (E) Percentage of saved trips as a function of Δ with k = 2 and k = 3. The theoretically possible maximum (dashed lines) of 50% for k = 2 and 66.7% for k = 3 are closely approximated. For Δ < 150 s (dotted line), the benefits of 3-sharing over 2-sharing are negligible.