Abstract
In this article we investigate the heat and mass transfer analysis in mixed convective radiative flow of Jeffrey fluid over a moving surface. The effects of thermal and concentration stratifications are also taken into consideration. Rosseland's approximations are utilized for thermal radiation. The nonlinear boundary layer partial differential equations are converted into nonlinear ordinary differential equations via suitable dimensionless variables. The solutions of nonlinear ordinary differential equations are developed by homotopic procedure. Convergence of homotopic solutions is examined graphically and numerically. Graphical results of dimensionless velocity, temperature and concentration are presented and discussed in detail. Values of the skin-friction coefficient, the local Nusselt and the local Sherwood numbers are analyzed numerically. Temperature and concentration profiles are decreased when the values of thermal and concentration stratifications parameters increase. Larger values of radiation parameter lead to the higher temperature and thicker thermal boundary layer thickness.
Introduction
The boundary layer flow of non-Newtonian fluids gains a special attention of the researchers because of its wide occurrence in the industrial and engineering processes. The most commonly involved fluids in industry and technology are categorized as non-Newtonian. Many of the materials used in biological sciences, chemical and petroleum industries, geophysics etc. are also known as the non-Newtonian fluids. The non-Newtonian fluids are further divided into three main classes namely differential, rate and integral types. The simplest subclass of non-Newtonian fluids is the rate type fluids. The present study involves the Jeffrey fluid model which falls into the category of rate type non-Newtonian fluids. This fluid model exhibits the properties of ratio of relaxation to retardation times and retardation time. This model is very popular amongst the investigators. Few studies regarding Jeffrey fluid model are mentioned in the references [1]–[5].
The better cooling rate in the manufacturing processes is very essential for the best quality final product. For such processes, a controlled cooling system is required. An electrically polymeric liquid seems to be a good candidate for such applications of polymer and metallurgy because here the flow can be controlled by an applied magnetic field. Further the magnetohydrodynamic (MHD) flows are quite prominent in MHD power generating systems, cooling of nuclear reactors, plasma studies, geothermal energy extraction and many others. Interesting investigations on MHD flows can be seen in the references [6]–[11]. The thermal radiation effects have pivotal role in the industrial and engineering processes. Such processes are performed at very high temperature under various non-isothermal conditions and in situations where convective heat transfer coefficients are smaller. The radiative heat transfer can be used in hypersonic flights, model of pertinent equipment, nuclear power plants, nuclear reactors, gas turbines, space vehicles etc. [12]–[15].
Influence of stratification is an important aspect in heat and mass transfer analysis. The formation or deposition of the layers is known as the stratification. This phenomenon occurs due to the change in temperature or concentration, or variations in both, or presence of various fluids or different densities. It is quite important and interesting to examine the effects of combined stratifications (thermal and concentration stratifications) in mixed convective flow past a surface when heat and mass transfer analysis is performed simultaneously. Investigation of doubly stratified flows is a subject of special attention nowadays because of its broad range of applications in industrial and engineering processes. Few practical examples of these applications include heat rejection into the environment such as rivers, seas and lakes, thermal energy storage systems like solar ponds, mixture in industrial, food and manufacturing processing, density stratification of the atmosphere etc. Having all such applications in view, Hayat et al. [16] provided an analysis to examine the thermal stratification effects in mixed convective flow of Maxwell fluid over a stretching surface. Simultaneous effects of thermal stratification and thermal radiation in stretched flow of thixotropic fluid are discussed by Shehzad et al. [17]. Ibrahim and Makinde [18] considered the effects of double stratifications in mixed convection flow of nanofluid past a vertical plate. Srinivasacharya and Upender [19] investigated the doubly stratified flow of micropolar fluid in the presence of an applied magnetic field. Soret and Dufour effects on doubly stratified flow of viscous fluid in a porous medium are studied by Srinivasacharya and Surender [20].
Here our main theme is to study the influences of thermal and concentration stratifications in mixed convection flow of Jeffrey fluid over a stretching sheet. Heat and mass transfer characteristics are encountered. Further, we considered the thermal radiation effect. Mathematical modelling is presented subject to boundary layer assumptions and Roseland's approximation. The governing nonlinear flow model is solved and homotopic solutions [21]–[35] of dimensionless velocity, temperature and concentration are presented. Physical quantities for various parameters of interest are examined. To our knowledge such analysis is not yet reported.
Governing Problems
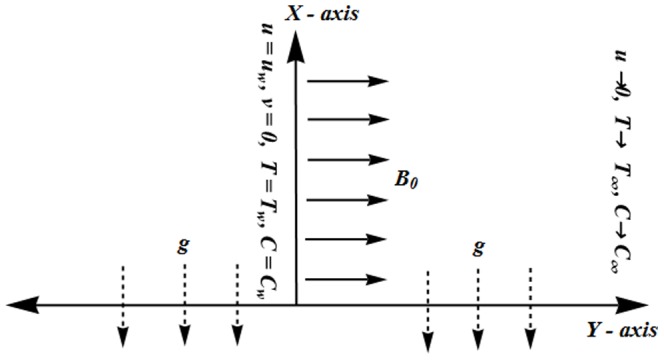
We consider the mixed convection flow of an incompressible Jeffrey fluid over a stretching surface. Thermal and concentration stratifications are taken into account in the presence of thermal radiation. The vertical surface has temperature 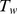 and concentration
and concentration 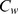 and further
and further 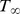 and
and 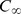 are the temperature and concentration of ambient fluid. The
are the temperature and concentration of ambient fluid. The  and
and 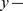 axes are chosen along and normal to the surface. The magnetic field of strength B0 is applied normal to the flow direction (see Fig. 1). The effects of induced magnetic field are neglected due to the low magnetic Reynolds number. The governing partial differential equations under boundary layer assumptions are given below [4], [14]:
axes are chosen along and normal to the surface. The magnetic field of strength B0 is applied normal to the flow direction (see Fig. 1). The effects of induced magnetic field are neglected due to the low magnetic Reynolds number. The governing partial differential equations under boundary layer assumptions are given below [4], [14]:
Figure 1. Physical model.
| (1) |
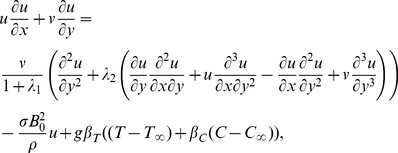 |
(2) |
| (3) |
| (4) |
where  and
and  denote the velocity components in the
denote the velocity components in the 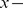 and
and 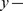 directions,
directions, 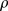 the fluid density,
the fluid density, 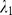 the ratio of relaxation to retardation times,
the ratio of relaxation to retardation times, 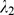 the retardation time,
the retardation time, 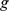 the gravitational acceleration,
the gravitational acceleration, 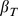 the thermal expansion coefficient,
the thermal expansion coefficient, 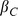 the concentration expansion coefficient,
the concentration expansion coefficient, 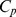 the specific heat at constant pressure,
the specific heat at constant pressure, 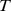 the fluid temperature,
the fluid temperature, 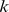 the thermal conductivity of fluid,
the thermal conductivity of fluid, 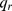 the radiative heat flux,
the radiative heat flux,  the fluid concentration and
the fluid concentration and 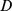 the diffusion coefficient.
the diffusion coefficient.
The subjected boundary conditions are [18]:
| (5) |
| (6) |
in which  is the stretching rate,
is the stretching rate, 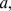
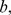
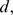
 are dimensional constants and
are dimensional constants and 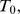
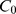 are the reference temperature and reference concentration, respectively.
are the reference temperature and reference concentration, respectively.
The radiative flux is accounted by employing the Rosseland assumption in the energy equation [12], [15]:
| (7) |
in which 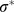 the Stefan-Boltzmann constant and
the Stefan-Boltzmann constant and 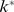 the mean absorption coefficient. Further, the differences of temperature within the flow is assumed to be small such that
the mean absorption coefficient. Further, the differences of temperature within the flow is assumed to be small such that 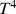 may be expressed as a linear function of temperature. Expansion of
may be expressed as a linear function of temperature. Expansion of 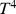 about
about 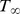 via Taylor's series and ignoring higher order terms, we have
via Taylor's series and ignoring higher order terms, we have
| (8) |
By employing Eqs. (7) and (8), Eq. (3) has the form
| (9) |
Setting
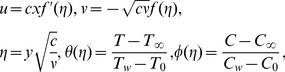 |
(10) |
equation (1) is satisfied automatically and reduced forms of Eqs. (7)–(10) and (13) are
| (11) |
| (12) |
| (13) |
and the boundary conditions in dimensionless form has the following form
| (14) |
| (15) |
Here 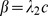 is the Deborah number,
is the Deborah number, 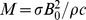 the magnetic parameter,
the magnetic parameter, 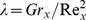 the thermal buoyancy parameter with
the thermal buoyancy parameter with 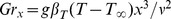 the local Grashof number and
the local Grashof number and 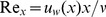 the local Reynolds number,
the local Reynolds number, 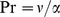 the Prandtl number,
the Prandtl number, 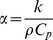 the thermal diffusivity,
the thermal diffusivity, 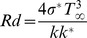 the thermal radiation parameter,
the thermal radiation parameter, 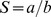 the thermal stratification parameter,
the thermal stratification parameter, 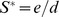 the concentration stratification parameter,
the concentration stratification parameter, 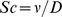 the Schmidt number and
the Schmidt number and 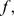
 and
and 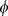 the dimensionless velocity, temperature and concentration, respectively.
the dimensionless velocity, temperature and concentration, respectively.
The skin friction coefficient, the local Nusselt number and the local Sherwood number are
| (16) |
where 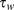 is the shear stress along the stretching surface,
is the shear stress along the stretching surface, 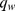 is the surface heat flux and
is the surface heat flux and 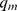 is the surface mass flux. The local skin-friction coefficient, local Nusselt and local Sherwood numbers in dimensionless forms are given below:
is the surface mass flux. The local skin-friction coefficient, local Nusselt and local Sherwood numbers in dimensionless forms are given below:
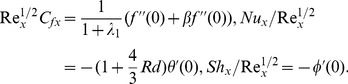 |
(17) |
Development of the Series Solutions
To develop the homotopic procedure [21]–[23], we choose the initial guesses and operators in the forms given below:
| (18) |
| (19) |
with
| (20) |
where 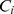
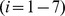 are the arbitrary constants. The zeroth order deformation equations together with the boundary conditions are
are the arbitrary constants. The zeroth order deformation equations together with the boundary conditions are
| (21) |
| (22) |
| (23) |
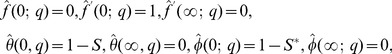 |
(24) |
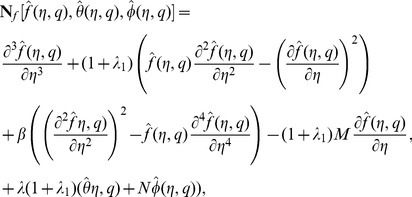 |
(25) |
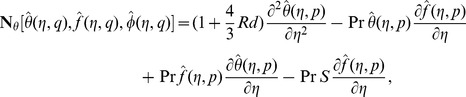 |
(26) |
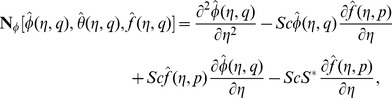 |
(27) |
where 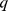 is an embedding parameter,
is an embedding parameter, 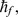
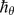 and
and 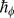 the non-zero auxiliary parameters and
the non-zero auxiliary parameters and 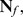
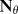 and
and 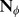 the nonlinear operators. For
the nonlinear operators. For 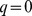 and
and 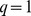 one has
one has
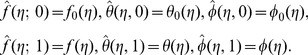 |
(28) |
When variation of  is taken into account from
is taken into account from  to
to  then
then 
 and
and 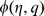 vary from
vary from 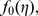
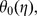
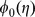 to
to 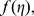
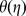 and
and 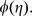 We expand
We expand 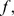
 and
and 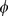 in the following forms [24]–[26]:
in the following forms [24]–[26]:
| (29) |
| (30) |
| (31) |
where the convergence of above series strongly depends upon 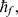
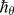 and
and 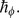 Considering that
Considering that 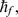
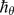 and
and 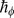 are selected properly such that Eqs. (29)–(31) converge for
are selected properly such that Eqs. (29)–(31) converge for 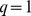 and thus [27], [28]:
and thus [27], [28]:
| (32) |
| (33) |
| (34) |
The general solutions are derived as follows:
| (35) |
| (36) |
| (37) |
where 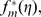
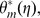 and
and 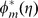 are the special solutions.
are the special solutions.
Analysis and Discussion
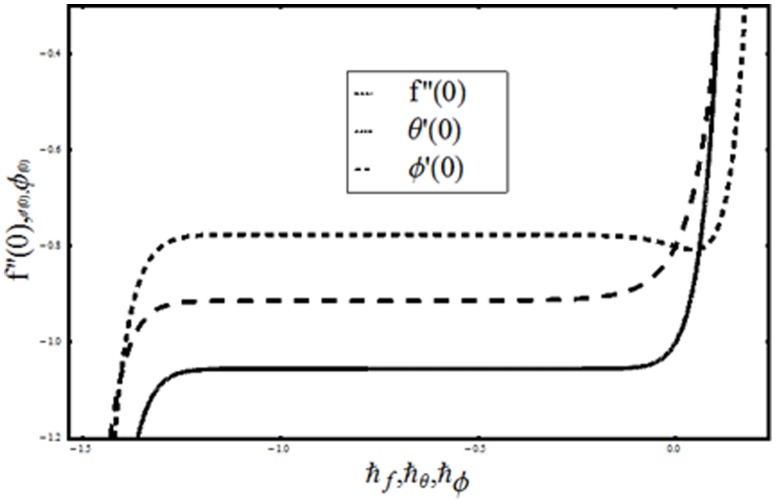
The coupled nonlinear ordinary differential equations are solved via homotopy analysis method. The convergence of derived homotopic solutions depend on the suitable values of auxiliary parameters 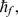
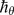 and
and 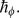 Hence the
Hence the 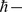 curves of functions
curves of functions 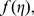
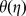 and
and 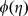 are drawn at
are drawn at 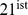 -order of approximations to choose the admissible values of
-order of approximations to choose the admissible values of 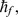
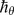 and
and 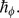 From Fig. 2 we have seen that the range of admissible values of
From Fig. 2 we have seen that the range of admissible values of 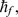
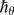 and
and 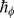 are
are 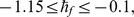
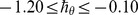 and
and 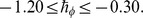 Table 1 also shows that the developed homotopic solutions are convergent in the whole region of
Table 1 also shows that the developed homotopic solutions are convergent in the whole region of 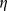 when
when 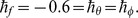
Figure 2.
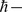 curves of functions
curves of functions 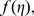
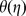 and
and 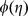 at 17th-order of deformations when
at 17th-order of deformations when 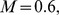
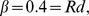
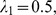
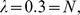
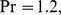
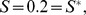
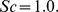 .
.
Table 1. Convergence of homotopy solution for different order of approximations when 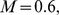
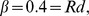
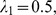
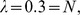
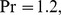
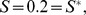
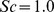 and
and 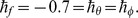 .
.
| Order of approximation |
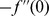
|
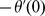
|
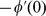
|
| 01 | 1.060200 | 0.790667 | 0.870000 |
| 10 | 1.055105 | 0.776083 | 0.913029 |
| 17 | 1.055116 | 0.776004 | 0.913502 |
| 24 | 1.055118 | 0.775996 | 0.913543 |
| 28 | 1.055118 | 0.775996 | 0.913547 |
| 35 | 1.055118 | 0.775996 | 0.913547 |
| 40 | 1.055118 | 0.775996 | 0.913547 |
The dimensionless velocity profile 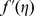 for different values of magnetic parameter
for different values of magnetic parameter 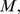 Deborah number
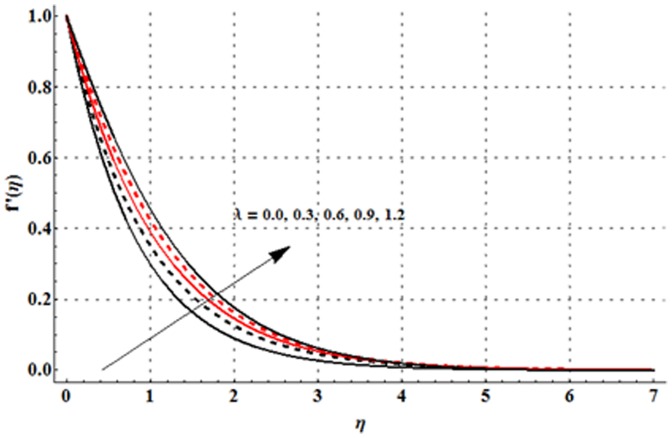
Deborah number 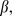 ratio of relaxation to retardation times
ratio of relaxation to retardation times 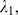 thermal buoyancy parameter
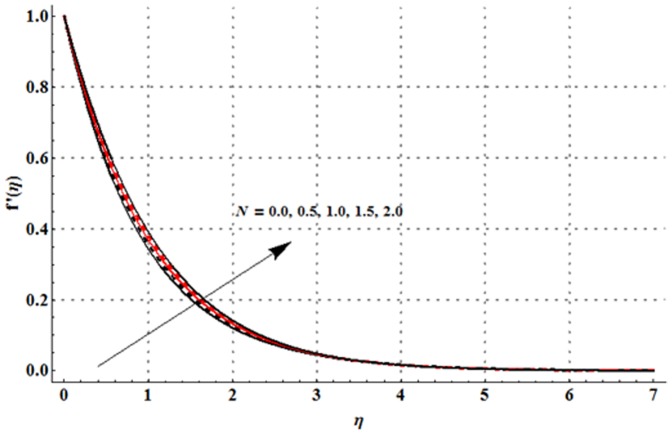
thermal buoyancy parameter 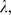 concentration buoyancy parameter
concentration buoyancy parameter 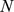 and radiation parameter
and radiation parameter 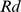 is sketched in the Figs. 3–8. It is noticed from Fig. 3 that the velocity profile and momentum boundary layer thickness is reduced when larger values of magnetic parameter are used. Here the magnetic parameter involves the Lorentz force. Lorentz force has an ability to resist the fluid flow. Such resistance in fluid flow leads to a reduction in the velocity profile. From Fig. 4 it is observed that larger Deborah number shows higher velocity and thicker momentum boundary layer thickness. From the definition of Deborah number, one can see that the Deborah number is directly proportional to the retardation time. Larger Deborah number has higher retardation time. Such higher retardation time gives rise to the fluid flow due to which the velocity profile is enhanced. Fig. 5 illustrates the impact of ratio of relaxation to retardation times on the velocity field. This Fig. shows that the velocity and its related boundary layer thickness are decreasing functions of ratio of relaxation to retardation times. Fig. 6 depicts that an increase in thermal buoyancy parameter leads to an increase in the velocity profile. Thermal buoyancy parameter depends on the buoyancy force. Larger buoyancy parameter has stronger buoyancy force. Such stronger buoyancy force acts as an agent and causes to an increase in the fluid velocity. Fig. 7 elucidates that both velocity profile and its related momentum boundary layer thickness are enhanced with an increase in the concentration buoyancy parameter. The change in velocity distribution function for various values of radiation parameter is examined in Fig. 8. Here we observed that the velocity distribution function is increased when we increase the values of radiation parameter.
is sketched in the Figs. 3–8. It is noticed from Fig. 3 that the velocity profile and momentum boundary layer thickness is reduced when larger values of magnetic parameter are used. Here the magnetic parameter involves the Lorentz force. Lorentz force has an ability to resist the fluid flow. Such resistance in fluid flow leads to a reduction in the velocity profile. From Fig. 4 it is observed that larger Deborah number shows higher velocity and thicker momentum boundary layer thickness. From the definition of Deborah number, one can see that the Deborah number is directly proportional to the retardation time. Larger Deborah number has higher retardation time. Such higher retardation time gives rise to the fluid flow due to which the velocity profile is enhanced. Fig. 5 illustrates the impact of ratio of relaxation to retardation times on the velocity field. This Fig. shows that the velocity and its related boundary layer thickness are decreasing functions of ratio of relaxation to retardation times. Fig. 6 depicts that an increase in thermal buoyancy parameter leads to an increase in the velocity profile. Thermal buoyancy parameter depends on the buoyancy force. Larger buoyancy parameter has stronger buoyancy force. Such stronger buoyancy force acts as an agent and causes to an increase in the fluid velocity. Fig. 7 elucidates that both velocity profile and its related momentum boundary layer thickness are enhanced with an increase in the concentration buoyancy parameter. The change in velocity distribution function for various values of radiation parameter is examined in Fig. 8. Here we observed that the velocity distribution function is increased when we increase the values of radiation parameter.
Figure 3. Influence of 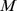 on the velocity profile
on the velocity profile 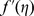 when
when 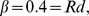
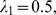
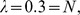
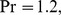
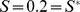 and
and 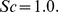 .
.
Figure 8. Influence of 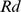 on the velocity profile
on the velocity profile 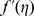 when
when 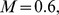
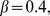
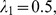
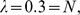
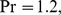
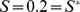 and
and 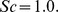 .
.
Figure 4. Influence of 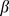 on the velocity profile
on the velocity profile 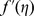 when
when 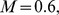
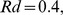
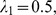
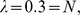
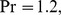
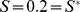 and
and 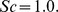 .
.
Figure 5. Influence of 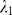 on the velocity profile
on the velocity profile 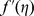 when
when 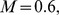
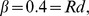
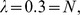
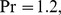
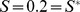 and
and 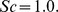 .
.
Figure 6. Influence of 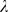 on the velocity profile
on the velocity profile 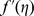 when
when 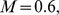
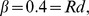
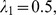
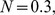
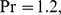
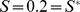 and
and 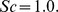 .
.
Figure 7. Influence of 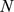 on the velocity profile
on the velocity profile 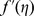 when
when 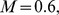
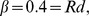
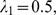
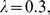
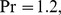
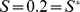 and
and 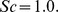 .
.
The variations in the non-dimensional temperature distribution function 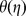 correspond to different values of magnetic parameter
correspond to different values of magnetic parameter 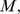 Deborah number
Deborah number 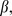 ratio of relaxation to retardation times
ratio of relaxation to retardation times 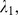 thermal buoyancy parameter
thermal buoyancy parameter 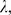 Prandtl number
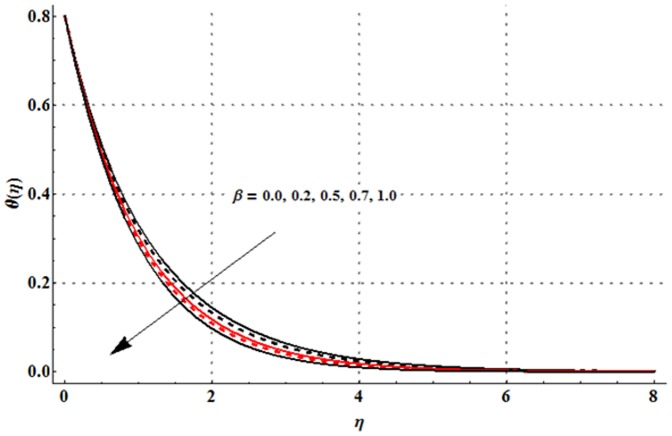
Prandtl number 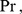 thermal stratification parameter
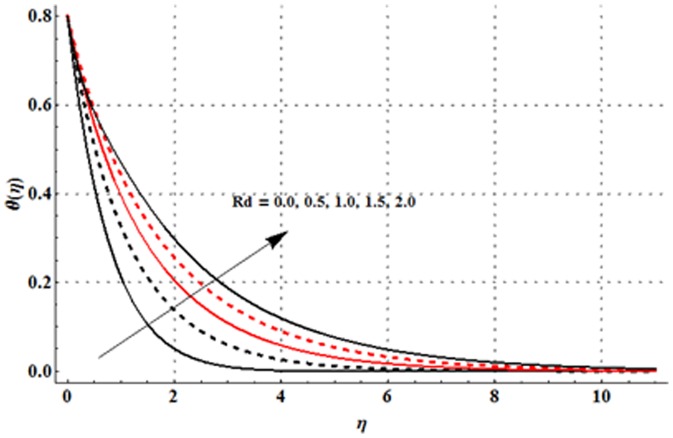
thermal stratification parameter 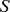 and radiation parameter
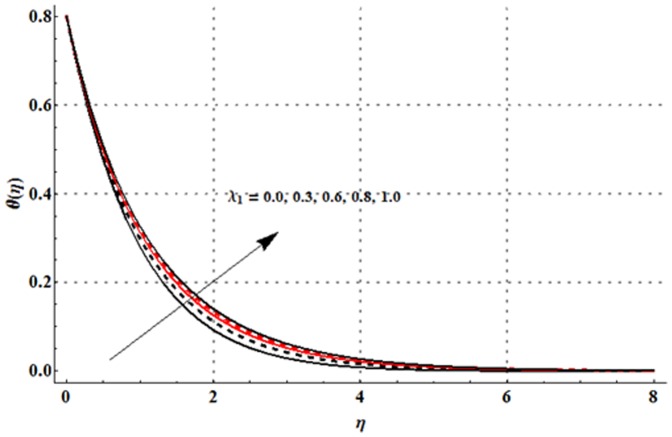
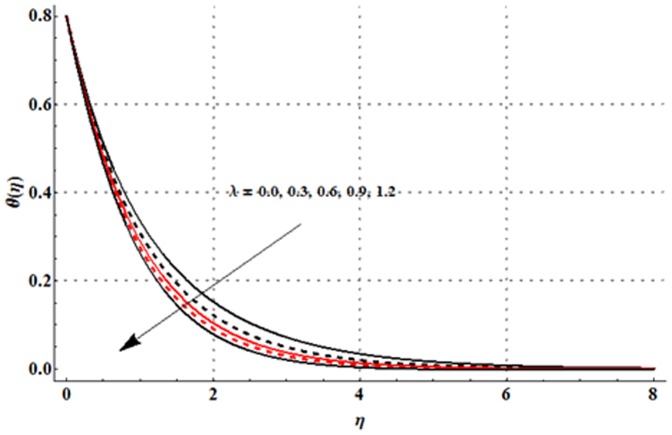
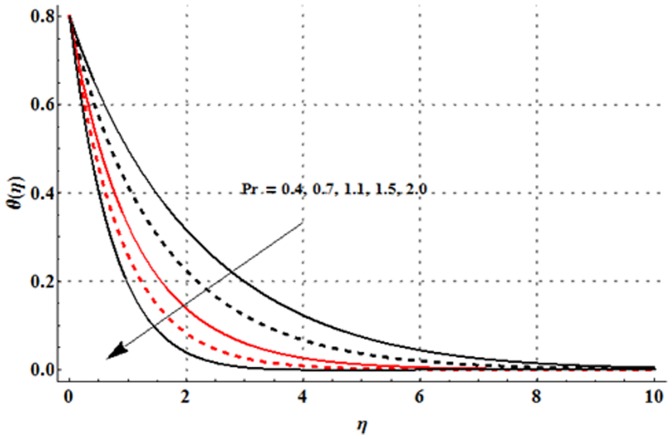
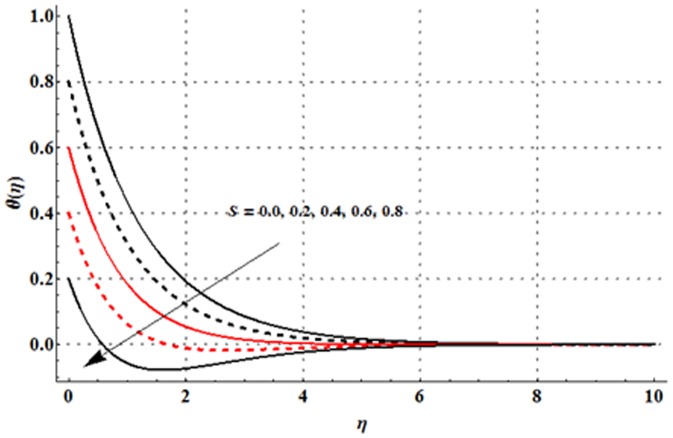
and radiation parameter 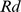 are examined in the Figs. 9–15. From Fig. 9 it is seen that the temperature profile and thermal boundary layer thickness are enhanced for the larger magnetic parameter. Here stronger Lorentz force corresponds to the larger magnetic parameter. This stronger Lorentz force has an ability to increase the temperature. Figs. 10 and 11 depict that the Deborah number and ratio of relaxation to retardation times have quite reverse effects on the temperature field and thermal boundary layer thickness. Temperature is decreased with an increase in the Deborah number but an enhancement in the temperature is observed for larger ratio of relaxation to retardation times. Fig. 12 illustrates that an increase in the thermal buoyancy parameter leads to a reduction in the temperature profile and thermal boundary layer thickness. From Fig. 13 we observed that lower temperature and thinner thermal boundary layer thickness correspond to an increase in the Prandtl number. Prandtl number is the ratio of momentum to thermal diffusivities. An enhancement in the Prandtl number implies to higher momentum diffusivity and lower thermal diffusivity. Such variation in momentum and thermal diffusivities shows a reduction in the temperature profile and thermal boundary layer thickness. Fig. 14 is sketched for temperature field when different values of thermal stratification parameter are taken into account. We have seen that the temperature profile is reduced when we increase the values of thermal stratification parameter. It is also noticed that the case of prescribed surface temperature is obtained when
are examined in the Figs. 9–15. From Fig. 9 it is seen that the temperature profile and thermal boundary layer thickness are enhanced for the larger magnetic parameter. Here stronger Lorentz force corresponds to the larger magnetic parameter. This stronger Lorentz force has an ability to increase the temperature. Figs. 10 and 11 depict that the Deborah number and ratio of relaxation to retardation times have quite reverse effects on the temperature field and thermal boundary layer thickness. Temperature is decreased with an increase in the Deborah number but an enhancement in the temperature is observed for larger ratio of relaxation to retardation times. Fig. 12 illustrates that an increase in the thermal buoyancy parameter leads to a reduction in the temperature profile and thermal boundary layer thickness. From Fig. 13 we observed that lower temperature and thinner thermal boundary layer thickness correspond to an increase in the Prandtl number. Prandtl number is the ratio of momentum to thermal diffusivities. An enhancement in the Prandtl number implies to higher momentum diffusivity and lower thermal diffusivity. Such variation in momentum and thermal diffusivities shows a reduction in the temperature profile and thermal boundary layer thickness. Fig. 14 is sketched for temperature field when different values of thermal stratification parameter are taken into account. We have seen that the temperature profile is reduced when we increase the values of thermal stratification parameter. It is also noticed that the case of prescribed surface temperature is obtained when 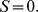 Physically, the difference between the surface temperature and ambient temperature is decreased when larger values of thermal stratification parameter are used. This change in surface and ambient temperatures leads to a decrease in the temperature profile. From Fig. 15 we noticed that higher temperature and thicker thermal boundary layer thickness correspond to the larger radiation parameter. Here larger radiation parameter gives more heat to fluid due to which the temperature profile is enhanced.
Physically, the difference between the surface temperature and ambient temperature is decreased when larger values of thermal stratification parameter are used. This change in surface and ambient temperatures leads to a decrease in the temperature profile. From Fig. 15 we noticed that higher temperature and thicker thermal boundary layer thickness correspond to the larger radiation parameter. Here larger radiation parameter gives more heat to fluid due to which the temperature profile is enhanced.
Figure 9. Influence of 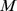 on the temperature profile
on the temperature profile 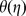 when
when 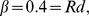
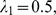
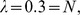
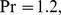
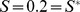 and
and 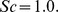 .
.
Figure 15. Influence of 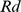 on the temperature profile
on the temperature profile 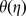 when
when 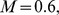
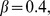
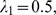
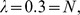
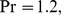
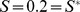 and
and 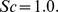 .
.
Figure 10. Influence of 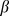 on the temperature profile
on the temperature profile 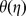 when
when 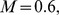
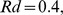
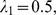
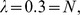
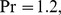
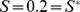 and
and 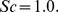 .
.
Figure 11. Influence of 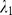 on the temperature profile
on the temperature profile 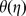 when
when 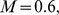
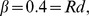
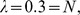
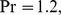
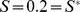 and
and 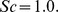 .
.
Figure 12. Influence of 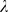 on the temperature profile
on the temperature profile 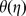 when
when 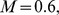
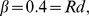
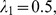
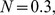
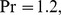
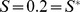 and
and 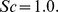 .
.
Figure 13. Influence of 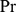 on the temperature profile
on the temperature profile 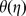 when
when 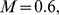
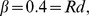
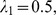
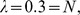
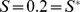 and
and 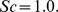 .
.
Figure 14. Influence of 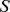 on the temperature profile
on the temperature profile 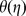 when
when 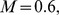
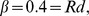
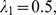
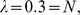
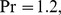
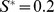 and
and 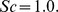 .
.
The effects of magnetic parameter 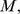 Deborah number
Deborah number 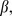 ratio of relaxation to retardation times
ratio of relaxation to retardation times 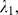 concentration stratification parameter
concentration stratification parameter 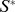 and Schmidt number
and Schmidt number 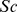 on the concentration field
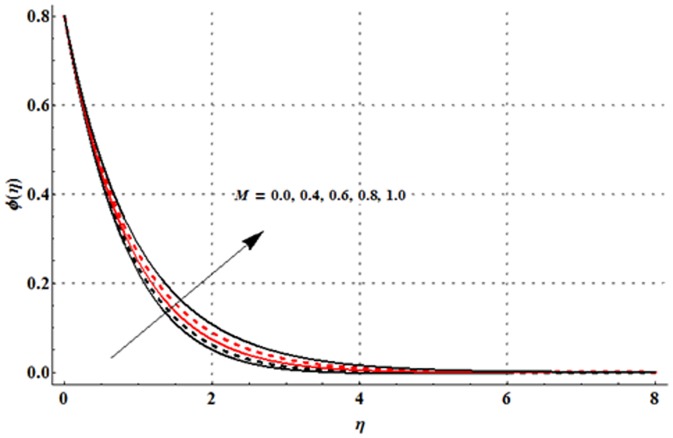
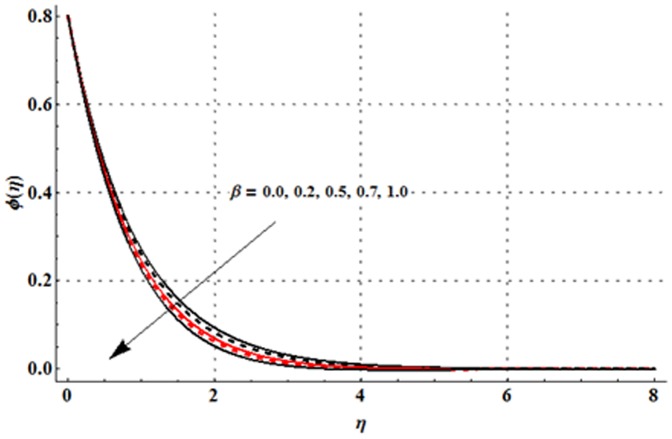
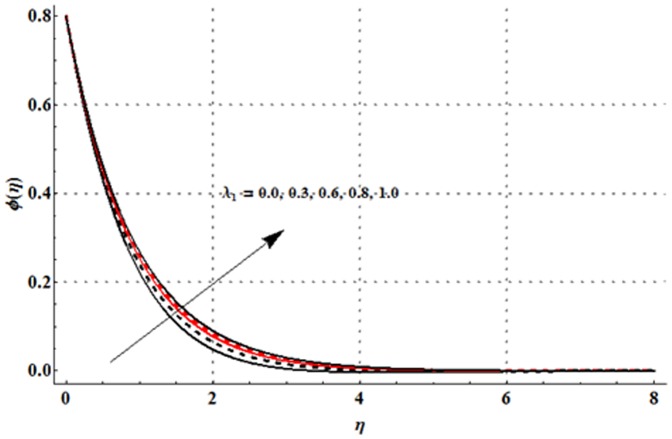
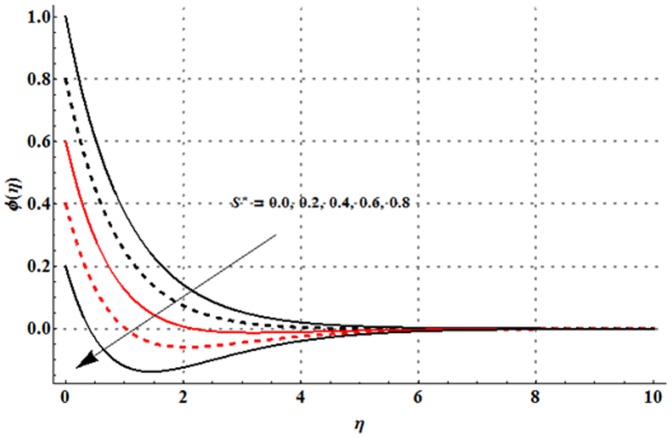
on the concentration field 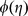 are shown in the Figs. 16–20. Fig. 16 elucidates that concentration profile and its associated boundary layer thickness are increased with an increase in the magnetic parameter. From Figs. 17 and 18, we observed that the concentration is decreased for larger Deborah number but the larger values of ratio of relaxation to retardation times give rise to the concentration field. Impact of concentration stratification parameter on the concentration profile is examined in Fig. 19. From this Fig. it is observed that the concentration profile is reduced with an increase in the concentration stratification parameter. Further prescribed surface concentration case is achieved when we use
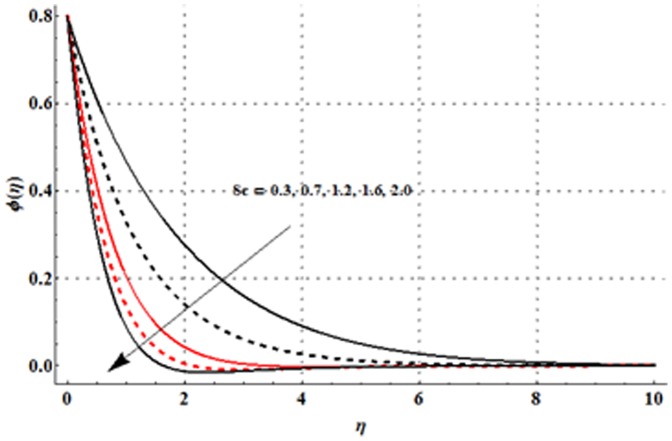
are shown in the Figs. 16–20. Fig. 16 elucidates that concentration profile and its associated boundary layer thickness are increased with an increase in the magnetic parameter. From Figs. 17 and 18, we observed that the concentration is decreased for larger Deborah number but the larger values of ratio of relaxation to retardation times give rise to the concentration field. Impact of concentration stratification parameter on the concentration profile is examined in Fig. 19. From this Fig. it is observed that the concentration profile is reduced with an increase in the concentration stratification parameter. Further prescribed surface concentration case is achieved when we use 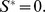 An increase in Schmidt number leads to a reduction in the concentration profile and its related boundary layer thickness (see Fig. 20).
An increase in Schmidt number leads to a reduction in the concentration profile and its related boundary layer thickness (see Fig. 20).
Figure 16. Influence of 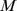 on the concentration profile
on the concentration profile 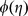 when
when 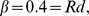
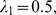
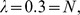
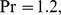
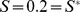 and
and 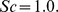 .
.
Figure 20. Influence of 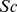 on the concentration profile
on the concentration profile 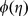 when
when 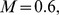
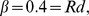
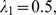
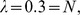
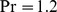 and
and 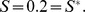 .
.
Figure 17. Influence of 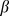 on the concentration profile
on the concentration profile 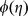 when
when 
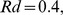
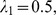
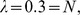
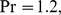
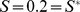 and
and 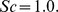 .
.
Figure 18. Influence of 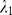 on the concentration profile
on the concentration profile 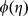 when
when 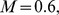
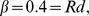
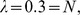
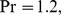
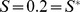 and
and 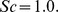 .
.
Figure 19. Influence of 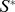 on the concentration profile
on the concentration profile 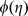 when
when 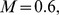
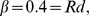
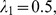
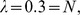
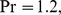
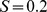 and
and 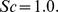 .
.
The numerical values of 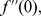
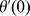 and
and 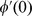 at different order of HAM approximations are analyzed in Table 1 when
at different order of HAM approximations are analyzed in Table 1 when 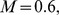
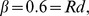
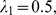
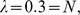
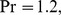
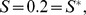
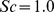 and
and 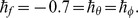 From this Table it is noticed that the values of
From this Table it is noticed that the values of 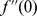 and
and 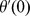 start to repeat from 24th-order of deformations. On the other hand the values of
start to repeat from 24th-order of deformations. On the other hand the values of 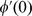 converge from 28th-order of approximations. Table 2 presents the numerical values of skin-friction coefficient for different values of
converge from 28th-order of approximations. Table 2 presents the numerical values of skin-friction coefficient for different values of 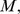
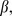
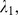
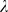 and
and 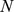 when
when 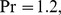
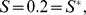
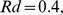 and
and 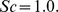 It is observed that the values of skin-friction coefficient are larger when we increase the values of
It is observed that the values of skin-friction coefficient are larger when we increase the values of 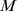 and
and 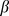 but these values are smaller for larger
but these values are smaller for larger 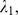
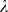 and
and 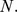 Table 3 is computed to examine the values of skin-friction coefficient for different values of
Table 3 is computed to examine the values of skin-friction coefficient for different values of 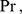

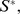
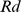 and
and 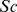 when
when 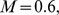
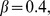
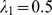 and
and 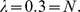 This Table shows that the values of skin-friction coefficient are increased with an increase in
This Table shows that the values of skin-friction coefficient are increased with an increase in 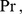
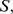
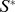 and
and 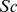 but a decrease is noticed for the larger
but a decrease is noticed for the larger 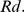 Numerical values of local Nusselt and Sherwood numbers for various values of
Numerical values of local Nusselt and Sherwood numbers for various values of 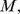
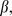
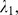
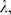
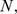
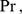
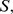
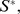
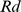 and
and 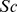 are observed in the Tables 4 and 5. From these Tables we have seen that the values of local Nusselt number are larger in comparison to the values of local Sherwood number when we used the values of
are observed in the Tables 4 and 5. From these Tables we have seen that the values of local Nusselt number are larger in comparison to the values of local Sherwood number when we used the values of 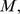

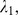
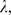
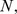
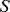 and
and 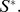
Table 2. Values of skin-friction coefficient 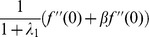 for different values of
for different values of 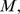
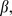
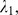
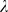 and
and 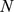 when
when 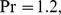
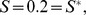
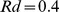 and
and 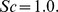 .
.
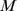
|
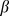
|
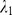
|
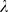
|
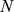
|
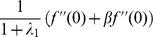
|
| 0.0 | 0.4 | 0.5 | 0.3 | 0.3 | 0.82197 |
| 0.4 | 0.89699 | ||||
| 0.8 | 1.09849 | ||||
| 0.6 | 0.0 | 0.5 | 0.3 | 0.3 | 0.81634 |
| 0.3 | 0.94515 | ||||
| 0.7 | 1.09609 | ||||
| 0.6 | 0.4 | 0.0 | 0.3 | 0.3 | 1.23185 |
| 0.6 | 0.95028 | ||||
| 1.0 | 0.84010 | ||||
| 0.6 | 0.4 | 0.5 | 0.0 | 0.3 | 1.12665 |
| 0.4 | 0.81119 | ||||
| 0.7 | 0.94018 | ||||
| 0.6 | 0.4 | 0.5 | 0.3 | 0.0 | 1.01394 |
| 0.4 | 0.97514 | ||||
| 0.7 | 0.94646 |
Table 3. Values of skin-friction coefficient 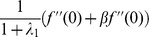 for different values of
for different values of 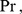
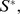
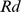 and
and 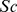 when
when 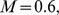
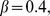
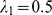 and
and 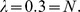 .
.
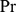
|
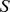
|
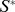
|
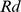
|
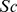
|
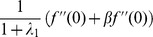
|
| 0.7 | 0.2 | 0.2 | 0.4 | 1.0 | 0.96396 |
| 1.0 | 0.97756 | ||||
| 1.3 | 0.98797 | ||||
| 1.2 | 0.0 | 0.2 | 0.4 | 1.0 | 0.94859 |
| 0.5 | 1.03868 | ||||
| 0.7 | 1.07436 | ||||
| 1.2 | 0.2 | 0.0 | 0.4 | 1.0 | 0.97432 |
| 0.5 | 1.00044 | ||||
| 0.7 | 1.01086 | ||||
| 1.2 | 0.2 | 0.2 | 0.0 | 1.0 | 1.00186 |
| 0.5 | 0.98145 | ||||
| 0.8 | 0.96839 | ||||
| 1.2 | 0.2 | 0.2 | 0.4 | 0.8 | 0.98212 |
| 2.0 | 0.99263 | ||||
| 2.5 | 0.99495 |
Table 4. Values of local Nusselt number 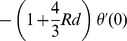 and local Sherwood number
and local Sherwood number 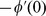 for different values of
for different values of 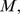
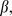
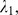
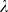 and
and 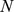 when
when 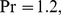
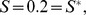
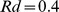 and
and 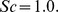 .
.
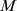
|
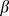
|
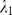
|
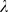
|
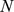
|
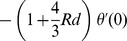
|
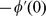
|
| 0.0 | 0.4 | 0.5 | 0.3 | 0.3 | 1.24653 | 0.95218 |
| 0.4 | 1.22027 | 0.93431 | ||||
| 0.8 | 1.15112 | 0.88693 | ||||
| 0.6 | 0.0 | 0.5 | 0.3 | 0.3 | 1.14034 | 0.87924 |
| 0.3 | 1.17885 | 0.90598 | ||||
| 0.7 | 1.21882 | 0.93328 | ||||
| 0.6 | 0.4 | 0.0 | 0.3 | 0.3 | 1.25054 | 0.95473 |
| 0.6 | 1.18031 | 0.90697 | ||||
| 1.0 | 1.14782 | 0.88445 | ||||
| 0.6 | 0.4 | 0.5 | 0.0 | 0.3 | 1.12659 | 0.87086 |
| 0.4 | 1.20514 | 0.92399 | ||||
| 0.7 | 1.24331 | 0.95029 | ||||
| 0.6 | 0.4 | 0.5 | 0.3 | 0.0 | 1.18090 | 0.90734 |
| 0.4 | 1.19273 | 0.91552 | ||||
| 0.7 | 1.20103 | 0.92126 |
Table 5. Values of local Nusselt number 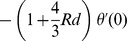 and local Sherwood number
and local Sherwood number 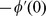 for different values of
for different values of 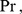
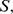
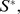
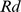 and
and 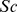 when
when 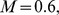
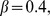
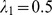 and
and 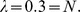 .
.
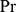
|
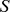
|
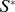
|
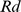
|
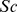
|
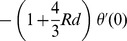
|
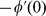
|
| 0.7 | 0.2 | 0.2 | 0.4 | 1.0 | 0.84401 | 0.93252 |
| 1.0 | 1.05959 | 0.91966 | ||||
| 1.3 | 1.25180 | 0.91100 | ||||
| 1.2 | 0.0 | 0.2 | 0.4 | 1.0 | 1.31047 | 0.92744 |
| 0.5 | 1.00330 | 0.89150 | ||||
| 0.7 | 0.87521 | 0.87585 | ||||
| 1.2 | 0.2 | 0.0 | 0.4 | 1.0 | 1.19544 | 0.99065 |
| 0.5 | 1.18137 | 0.79709 | ||||
| 0.7 | 1.17562 | 0.71897 | ||||
| 1.2 | 0.2 | 0.2 | 0.0 | 1.0 | 1.01578 | 0.90118 |
| 0.5 | 1.22660 | 0.91628 | ||||
| 0.8 | 1.32621 | 0.92373 | ||||
| 1.2 | 0.2 | 0.2 | 0.4 | 0.8 | 1.19275 | 0.78950 |
| 2.0 | 1.18395 | 1.40976 | ||||
| 2.5 | 1.18275 | 1.61211 |
Conclusions
We examined the effects of thermal and concentration stratifications in mixed convective radiative flow of Jeffrey fluid in this attempt. The main observations that we found in this investigation are as follows:
We have to compute 28th-order of HAM deformations for the convergent solutions.
Deborah number
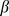 and ratio of relaxation to retardation times have reverse effects on the velocity profile
and ratio of relaxation to retardation times have reverse effects on the velocity profile 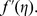
The effects of thermal buoyancy parameters on the velocity field
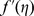 are more pronounced in comparison to concentration buoyancy parameter.
are more pronounced in comparison to concentration buoyancy parameter.An increase in thermal stratification parameter
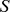 leads to a reduction in the temperature field and thermal boundary layer thickness.
leads to a reduction in the temperature field and thermal boundary layer thickness.The temperature profile and thermal boundary layer thickness are enhanced when radiation parameter
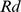 is increased.
is increased.The concentration field and its associated boundary layer thickness are decreasing functions of concentration stratification parameter
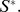
Numerical values of skin-friction coefficient are increased by increasing
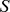 and
and 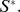
The larger values of
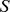 and
and 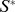 correspond to the lower values of local Nusselt and local Sherwood numbers.
correspond to the lower values of local Nusselt and local Sherwood numbers.
Data Availability
The authors confirm that all data underlying the findings are fully available without restriction. All relevant data are included within the paper.
Funding Statement
This project is funded by the Deanship of Scientific Research (DSR) King Abdulaziz University, Jeddah, Saudi Arabia under grant no. 78-130-35-HiCi. The authors, therefore, acknowledge with thanks DSR. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Kothandapani M, Srinivas S (2008) Peristaltic transport of a Jeffrey fluid under the effect of magnetic field in an asymmetric channel. Int J Non-Linear Mech 43: 915–924. [Google Scholar]
- 2. Tripathi D, Ali N, Hayat T, Chaube MK, Hendi AA (2011) Peristaltic flow of MHD Jeffrey fluid through a finite length cylindrical tube. Appl Math Mech-Engl Edit 32: 1148–1160. [Google Scholar]
- 3. Hayat T, Shehzad SA, Qasim M, Obaidat S (2012) Radiative flow of Jeffery fluid in a porous medium with power law heat flux and heat source. Nuclear Eng Design 243: 15–19. [Google Scholar]
- 4. Turkyilmazoglu M, Pop I (2013) Exact analytical solutions for the flow and heat transfer near the stagnation point on a stretching/shrinking sheet in a Jeffrey fluid. Int J Heat Mass Transfer 57: 82–88. [Google Scholar]
- 5. Shehzad SA, Alsaadi FE, Monaquel SJ, Hayat T (2013) Soret and Dufour effects on the stagnation point flow of Jeffery fluid with convective boundary conditions. Europ Phys J Plus 128: 56. [Google Scholar]
- 6. Ramzan M, Farooq M, Alsaedi A, Hayat T (2013) MHD three-dimensional flow of couple stress fluid with Newtonian heating. Europ Phys J Plus 128: 49. [Google Scholar]
- 7. Sheikholeslami M, Gorji-Bandpy M, Ganji DD (2013) Numerical investigation of MHD effects on Al2O3-water nanofluid flow and heat transfer in a semi-annulus enclosure using LBM. Energy 60: 501–510. [Google Scholar]
- 8. Rashidi MM, Abelman S, Mehr NF (2013) Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int J Heat Mass Transfer 62: 515–525. [Google Scholar]
- 9. Makinde OD, Khan WA, Khan ZH (2013) Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet. Int J Heat Mass Transfer 62: 526–533. [Google Scholar]
- 10. Turkyilmazoglu M (2013) The analytical solution of mixed convection heat transfer and fluid flow of a MHD viscoelastic fluid over a permeable stretching surface. Int J Mech Sci 77: 263–268. [Google Scholar]
- 11. Shehzad SA, Alsaedi A, Hayat T (2013) Hydromagnetic steady flow of Maxwell fluid over a bidirectional stretching surface with prescribed surface temperature and prescribed surface heat flux. Plos One 8: e68139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Turkyilmazoglu M, Pop I (2013) Heat and mass transfer of unsteady natural convection flow of some nanofluids past a vertical infinite flat plate with radiation effect. Int J Heat Mass Transfer 59: 167–171. [Google Scholar]
- 13. Hayat T, Waqas M, Shehzad SA, Alsaedi A (2013) Mixed convection radiative flow of Maxwell fluid near a stagnation point with convective condition. J Mech 29: 403–409. [Google Scholar]
- 14. Shehzad SA, Alsaedi A, Hayat T (2013) Influence of thermophoresis and Joule heating on the radiative flow of Jeffrey fluid with mixed convection. Braz J Chem Eng 30: 897–908. [Google Scholar]
- 15. Moradi A, Ahmadikia H, Hayat T, Alsaedi A (2013) On mixed convection radiation interaction about an inclined plate through a porous medium. Int J Thermal Sci 64: 129–136. [Google Scholar]
- 16. Hayat T, Shehzad SA, Al-Sulami HH, Asghar S (2013) Influence of thermal stratification on the radiative flow of Maxwell fluid. J Braz Soc Mech Sci Eng 35: 381–389. [Google Scholar]
- 17. Shehzad SA, Qasim M, Alsaedi A, Hayat T, Alhuthali MS (2013) Combined effects of thermal stratification and thermal radiation in mixed convection flow of thixotropic fluid. Europ Phys J Plus 128: 7. [Google Scholar]
- 18. Ibrahim W, Makinde OD (2013) The effect of double stratification on boundary-layer flow and heat transfer of nanofluid over a vertical plate. Comput Fluids 86: 433–441. [Google Scholar]
- 19. Srinivasacharya D, Upendar M (2013) Effect of double stratification on MHD free convection in a micropolar fluid. J Egypt Math Soc 21: 370–378. [Google Scholar]
- 20. Srinivasacharya D (2014) Surender (2014) Non-Darcy mixed convection in a doubly stratified porous medium with Soret-Dufour effects. Int J Eng Math 2014: 126218. [Google Scholar]
- 21. Liao SJ (2009) Notes on the homotopy analysis method: Some definitions and theorems. Commun Nonlinear Sci Numer Simulat 14: 983–997. [Google Scholar]
- 22. Turkyilmazoglu M (2010) A note on the homotopy analysis method. Appl Math Lett 23: 1226–1230. [Google Scholar]
- 23. Turkyilmazoglu M (2012) Solution of the Thomas-Fermi equation with a convergent approach. Commun Nonlinear Sci Numer Simulat 17: 4097–4103. [Google Scholar]
- 24. Zhang W, Qian YH, Lai SK (2012) Extended homotopy analysis method for multi-degree-of-freedom non-autonomous nonlinear dynamical systems and its application. Acta Mech 223: 2537–2548. [Google Scholar]
- 25. Sheikholeslami M, Ashorynejad HR, Domairry G, Hashim I (2012) Flow and heat transfer of cu-water nanofluid between a stretching sheet and a porous surface in a rotating system. J Appl Math 2012: 421320. [Google Scholar]
- 26. Rashidi MM, Ali M, Freidoonimehr N, Nazari F (2013) Parametric analysis and optimization of entropy generation in unsteady MHD flow over a stretching rotating disk using artificial neural network and particle swarm optimization algorithm. Energy 55: 497–510. [Google Scholar]
- 27. Abbasbandy S, Hashemi MS, Hashim I (2013) On convergence of homotopy analysis method and its application to fractional integro-differential equations. Quaestiones Mathematicae 36: 93–105. [Google Scholar]
- 28. Hayat T, Naseem A, Farooq M, Alsaedi A (2013) Unsteady MHD three-dimensional flow with viscous dissipation and Joule heating. Europ Phys J Plus 128: 158. [Google Scholar]
- 29. Alsaadi FE, Shehzad SA, Hayat T, Monaquel SJ (2013) Soret and Dufour effects on the unsteady mixed convection flow over a stretching surface. J Mech 29: 623–632. [Google Scholar]
- 30. Hayat T, Shehzad SA, Al-Mezel S, Alsaedi A (2014) Three-dimensional flow of an Oldroyd-B fluid over a bidirectional stretching surface with prescribed surface temperature and prescribed surface heat flux. J Hydrol Hydromech 62: 117–125. [Google Scholar]
- 31. Hayat T, Shehzad SA, Qasim M, Asghar S (2014) Three-dimensional stretched flow via convective boundary conditions and heat generation/absorption. Int J Numer Methods Heat Fluid Flow 24: 342–358. [Google Scholar]
- 32. Abbasbandy S, Hayat T, Alsaedi A, Rashidi MM (2014) Numerical and analytical solutions for Falkner-Skan flow of MHD Oldroyd-B fluid. Int J Numer Methods Heat Fluid Flow 24: 390–401. [Google Scholar]
- 33. Shehzad SA, Alsaedi A, Hayat T, Alhuthali MS (2013) Three-dimensional flow of an Oldroyd-B fluid with variable thermal conductivity and heat generation/absorption. Plos One 8: e78240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Hayat T, Shehzad SA, Alsaedi A (2013) Three-dimensional stretched flow of Jeffery fluid with variable thermal conductivity and thermal radiation. Appl Math Mech-Eng Edit 34: 823–832. [Google Scholar]
- 35. Hayat T, Asad S, Mustafa M, Alsaedi A (2014) Radiation effects on the flow of Powell-Eyring fluid past an unsteady inclined stretching sheet with non-uniform heat source/sink. Plos One 9: e103214. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The authors confirm that all data underlying the findings are fully available without restriction. All relevant data are included within the paper.