Assessment of amide I spectroscopic maps for a gas-phase peptide using IR-UV double-resonance spectroscopy and density functional theory calculations

Abstract

The spectroscopy of amide I vibrations has become a powerful tool for exploring protein structure and dynamics. To help with spectral interpretation, it is often useful to perform molecular dynamics (MD) simulations. To connect spectroscopic experiments to simulations in an efficient manner, several researchers have proposed “maps,” which relate observables in classical MD simulations to quantum spectroscopic variables. It can be difficult to discern whether errors in the theoretical results (compared to experiment) arise from inaccuracies in the MD trajectories or in the maps themselves. In this work, we evaluate spectroscopic maps independently from MD simulations by comparing experimental and theoretical spectra for a single conformation of the α-helical model peptide Ac-Phe-(Ala)₅-Lys-H⁺ in the gas phase. Conformation-specific experimental spectra are obtained for the unlabeled peptide and for several singly and doubly ¹³C-labeled variants using infrared-ultraviolet double-resonance spectroscopy, and these spectra are found to be well-modeled by density functional theory (DFT) calculations at the B3LYP/6-31G** level. We then compare DFT results for the deuterated and ¹³C¹⁸O-labeled peptide with those from spectroscopic maps developed and used previously by the Skinner group. We find that the maps are typically accurate to within a few cm⁻¹ for both frequencies and couplings, having larger errors only for the frequencies of terminal amides.

I. INTRODUCTION

The elucidation of the structural and dynamical properties of proteins is among the most rich, challenging, and relevant problems in chemical physics. The vast array of possible primary sequences gives rise to an even larger number of protein conformations, and understanding these conformations and the transitions between them is fundamental for many problems in health and biological engineering. One family of techniques that has recently proven useful in addressing these problems involves the infrared (IR) spectroscopy of the amide I (mostly CO stretch) vibration of the peptide bonds of proteins. Researchers have found that the amide I IR line shape of proteins is sensitive both to local environments and to the couplings between different amide chromophores. These couplings often lead to unique spectral features for different secondary structures.^1–3

IR spectroscopy suffers, however, from ambiguities in the interpretation of experimental data. The IR line shapes of proteins generally consist of overlapping contributions from a multitude of structures that interconvert on a variety of timescales, and there can be multiple ways to decompose the line shape into contributions from different structures. Thus, IR line shapes frequently permit interpretation in terms of multiple underlying structural models. To discriminate more effectively between these models, many researchers have turned to molecular dynamics (MD) simulation, which provides the positions of all sites (frequently all atoms) at each time step. This method, however, suffers from potential disconnects with reality, as the accuracy of the force fields employed can be questionable. In fact, it is well-known that different protein force fields may give rise to substantially different structures and dynamics even for simple peptides.⁴

In order to make a direct connection between simulation and experiment, a number of researchers have proposed methods by which amide I IR line shapes can be calculated from classical MD simulations.^5–16 To the extent that the experimental and calculated spectra agree, one may with greater justification trust results from MD simulations, and use those results to interpret experimental spectra. Amide I spectra are typically calculated using a frequency “map,” which parameterizes the local-mode frequencies as a function of MD electrostatic potentials, fields, or field gradients on atoms involved in the amide I vibration.^{5,6,8,9,13–18} Maps have also been proposed for calculating nearest-neighbor frequency shifts, amide I transition dipoles, and vibrational couplings as a function of peptide geometry.^5,10,18–24 Although it is possible to avoid these parameterizations by calculating spectra using electronic-structure methods,^12,25–30 spectroscopic maps possess important advantages in computational cost. Whereas electronic-structure calculations are limited either to fairly small systems or to static structures, methods based on classical force fields can be employed to calculate spectra for hundreds of chromophores over hundreds of nanoseconds, allowing for more extensive sampling of protein conformational landscapes and for the incorporation of dynamical effects.

In this work, we specifically examine the amide I spectroscopic maps recently employed by the Skinner group.^14,31–33 In our maps, the amide I frequency is computed as a function of components of the MD electric fields on the C and N atoms of the amide. The maps include three parameters: two describing the effect of electric fields on the amide C and N atoms, and a zero-field intercept. The parameters were chosen so as to reproduce experimental data for the peak position and line width of the N-deuterated model peptide N-methylacetamide (NMAD) in D₂O, dimethylsulfoxide (DMSO), and chloroform when calculating spectra from simulations using the GROMOS96 53a6 force field.³⁴ For non-nearest-neighbor couplings, we use a parameterization by Torii and Tasumi²² that describes the amide I transition dipole as a function of the coordinates of the amide C, O, and N atoms, and models couplings via transition dipole interactions. For nearest-neighbor frequency shifts and couplings, we employ Ramachandran angle-based maps from Jansen and co-workers.¹⁰

To test the accuracy of spectroscopic maps, a number of authors have performed detailed comparisons of simulated frequencies, couplings, and line shapes to experimental data for a variety of peptide sizes and secondary structures.^15,35–42 In particular, a previous analysis of our maps relied on a comparison to two-dimensional IR data for an isotope-labeled, macrocylic, parallel β-peptide.³³ However, spectroscopic calculations are subject to errors both in the generation of conformations via MD simulation and in the application of the maps, and the extent to which each of these effects is responsible for the error in computed spectra is typically unclear. MD simulations can be avoided by benchmarking map results against electronic-structure calculations, in which case the conformations treated using maps or electronic structure are known to be the same.^{10,26,43–47} However, possible errors in the electronic-structure calculations then become a concern. Accordingly, one would really like to connect the results to experimental data for a peptide in a known conformation. In this work, therefore, we address the errors inherent in our maps by examining the spectrum of a single conformation of a model peptide in the gas phase. (A similar approach was taken in recent work by Buchanan et al.^48,49) Specifically, we examine the model α-helix Ac-Phe-(Ala)₅-Lys-H⁺ (Ac-FA5K).

To perform this study, it is necessary to acquire reliable amide I spectra for a single conformation of Ac-FA5K. In previous work, the Rizzo group^50,51 has presented conformation-specific NH- and OH-stretch spectra for this peptide using infrared-ultraviolet (IR-UV) double-resonance spectroscopy. In this method, cold (∼10 K) gas-phase peptides are isolated in an ion trap using electrospray ionization. Photofragmentation is induced using a UV laser that excites an electronic transition of the phenylalanine ring, and the electronic spectrum is quite sensitive to the peptide conformation. The IR spectrum of a single conformation of the peptide can be obtained by introducing an IR pulse prior to the UV pulse. When a system vibration is resonant with the IR frequency, causing the peptide to become vibrationally excited, the population of ground-state Ac-FA5K is diminished. The IR spectrum can thus be measured as a depletion in the photofragmentation signal between the IR-on and IR-off conditions.

In addition to the native peptide, experimental spectra are also obtained for several singly or doubly ¹³C-labeled isotopomers of Ac-FA5K. ¹³C labeling reduces the amide I frequency by ∼40 cm⁻¹, diminishing the effect of couplings between the labeled and unlabeled amides and allowing for a better characterization of individual frequencies (using single labels) and couplings (using double labels).^52–54

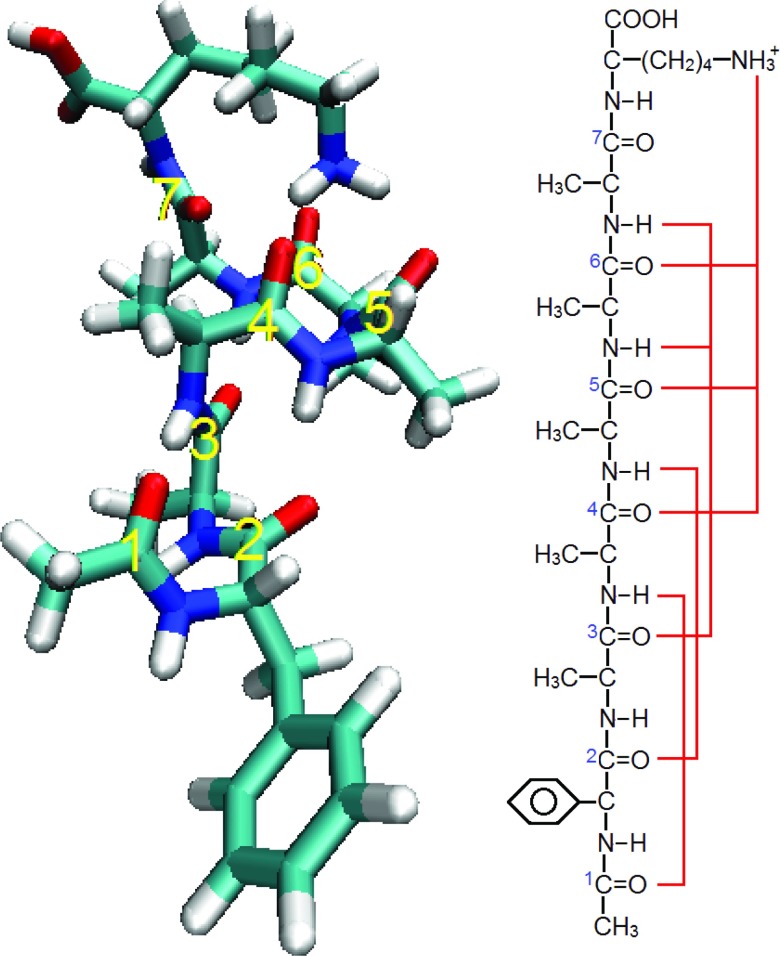
To correlate the experimental data with a microscopic conformation, one can perform a conformational search using a classical force field, followed by energy minimization and frequency calculation using an electronic structure method. The experimental peptide conformation can then be identified by searching for the best match between the experimental and theoretical IR frequencies and intensities. In previous work, several conformations of Ac-FA5K were identified in this way, by comparing NH-stretch spectra from experiment and from density functional theory (DFT).⁵¹ In Figure 1, one of these structures (structure “B” in the previous study⁵¹) is shown, along with a schematic depicting the hydrogen bonding pattern of its amide I residues. Note that this peptide possesses seven amide I chromophores, all of which are located on the peptide backbone.

FIG. 1.

(Left) VMD snapshot showing the conformation of Ac-FA5K studied in this work, with labels showing the seven amide chromophores. (Right) Diagram of the molecular structure of Ac-FA5K, with red lines showing hydrogen bonds to the amide groups.

In this work, we first present experimental and DFT amide I spectra for this conformation of Ac-FA5K, both for the native peptide and for singly or doubly ¹³C-labeled isotopomers. Excellent agreement between the experimental and DFT results is observed (as might indeed be expected based on previous work^55–57), reinforcing our identification of the experimental structure and validating our DFT calculations. We then compare the DFT results to results from our spectroscopic maps. For this comparison, we consider the deuterated peptide, since our maps are actually developed for deuterated amide vibrations. Of particular interest is a direct comparison between our maps and DFT for the local-mode frequencies and couplings between modes. To this end, we consider the deuterated peptide with single and double ¹³C¹⁸O labels. For the former, the labeled groups are decoupled from the other modes (even more so than with ¹³C labels), so we can determine their frequencies directly from the DFT calculations. For the latter, the labeled pair is decoupled from the other modes, and we can deduce the coupling from the frequency shift of the labeled modes as compared to the results for single labels. Both frequencies and couplings are then compared directly with map predictions. In this way, we are able to characterize the reliability of the maps in a more thorough and clear manner than has previously been achieved.

II. METHODS

A. Synthesis and double-resonance spectroscopy of the Ac-Phe-(Ala)₅-Lys-H⁺ peptide in the amide I spectral region

The Ac-FA5K peptides were synthesized using solid-phase Fmoc chemistry on an Applied Biosystems 433A synthesizer and purified by high-performance liquid chromatography. For the synthesis of singly and doubly isotope-labeled samples, carbon-13 substituted L-alanine of 99% isotopic purity (CortecNet) was used.

The experimental setup for the spectroscopic studies is described in detail elsewhere.⁵⁸ Briefly, gas-phase, protonated peptides are produced at atmospheric pressure using nano-electrospray from a 0.1 M solution in 50:50:0.1 methanol:water:acetic acid. A metal capillary samples the nanospray plume and draws ions into the vacuum chamber, where they are mass-selected by a quadrupole mass filter and guided into a 22-pole RF ion trap, which is cooled to 6 K by a closed cycle refrigerator. A pulse of helium introduced into the trap before the arrival of the ion packet collisionally cools the ions to ∼10 K. Approximately 40 ms later, a UV laser pulse (or combination of IR and UV pulses) is sent through the trap to excite the cold ions. After a short delay (10 μs–2 ms), parent ions and charged fragments resulting from the absorption of UV photons are released from the trap, passed through a second quadrupole mass filter that selects either fragment or parent ions, and detected with a channeltron detector.

The electronic spectrum of the cold, protonated peptide ions is measured by recording the photofragment ion signal as a function of the UV wavelength. Since isotopic labeling does not change the electronic properties of the peptide, electronic spectra for singly and doubly ¹³C-labeled Ac-FA5K appear identical to that reported previously for unlabeled Ac-FA5K.⁵⁰ Conformer-specific vibrational spectra of the cold ions are then recorded by fixing the UV laser on a particular feature in the electronic spectrum, and introducing an IR laser pulse that precedes the UV pulse by 150 ns.⁵⁹ When the IR laser frequency is resonant with a ground state vibrational band of the peptide, IR absorption removes population from the ground state, resulting in a depletion of the UV-induced photofragmentation signal. This depletion is recorded as a function of IR frequency to obtain a conformer-specific IR spectrum.

UV laser pulses are produced by doubling the frequency of a Nd:YAG pumped dye laser (Lumonics) using a BBO crystal. IR laser pulses in the range 1300–2000 cm⁻¹ are produced by mixing the signal and idler beams from an infrared OPO (LaserVision) in a AgGaSe2 crystal.

B. Previous DFT calculations

Previously, Stearns et al.⁵¹ performed DFT calculations to determine the lowest-energy conformations of Ac-FA5K, which were validated using the IR spectra of cold ions in the NH-stretch region. The initial conformational search was performed in Macromodel⁶⁰ using the AMBER force field,⁶¹ and the most favorable structures were further optimized in Gaussian 03⁶² at the B3LYP/6-31G** level.^63–67 Vibrational frequencies were calculated for the 21 most stable conformations and scaled by a factor of 0.952 for comparison to the NH-stretch frequencies. (Note that this factor is different from the one used below for comparison of amide I frequencies. The scaling factor acts primarily to compensate for the failure to consider vibrational anharmonicity in the electronic structure calculations, and different scaling factors are required for vibrations with different anharmonicities.)

The structure assigned to conformer B of Ac-FA5K is a helix with a C₁₀–C₁₀–C₁₀–C₁₃ hydrogen-bonding pattern and a g-orientation of the phenylalanine side chain.⁵¹ This conformer, which is the object of the present work, is depicted in Figure 1.

C. DFT calculation of amide I IR spectra

Amide I spectra of Ac-FA5K were computed using Gaussian 09.⁶⁸ First, the minimum-energy geometry of the relevant configuration of Ac-FA5K at the B3LYP/6-31G** level was found; the use of analytic gradients was necessary to achieve convergence. Harmonic frequency analysis was then performed including all degrees of freedom, for the following isotope conditions:

• 1.Unlabeled (with ¹H, ¹²C, and ¹⁶O),
• 2.¹³C-labeled at the experimental locations,
• 3.D-labeled at all backbone amide groups and at the Lys amine group, and both unlabeled and ¹³C¹⁸O-labeled at the backbone amide groups for all single and double labels.

The first two isotope conditions are employed to compare DFT results with experiment. The last isotope condition is used for comparison with results from spectroscopic maps. D-labeling at the amide groups is necessary because the maps are parameterized for NMAD rather than its fully protonated isotopomer NMA, since amide I spectra of proteins are typically collected in D₂O (the water bending mode would interfere with the amide I stretch in a protonated, aqueous system).¹⁴ D-labeling at the Lys amine group is necessary because this group possesses a bending mode near 1640 cm⁻¹ in the fully protonated system. Because amides 4, 5, and 6 all hydrogen-bond to this group (see Figure 1), their amide I frequencies are influenced quite strongly by coupling to the Lys bend, which is not accounted for by the maps; deuteration shifts the Lys bend to much lower frequency (∼1210 cm⁻¹), removing this effect. Finally, we employ ¹³C¹⁸O-labeling in the calculation to minimize coupling effects between labeled and unlabeled amides (by shifting the local modes further out of resonance with the unlabeled band). Although ¹³C¹⁸O-labeling creates the possibility of coupling to a phenyl ring-breathing mode near 1610 cm⁻¹, this coupling was found to affect the amide I frequencies very little.

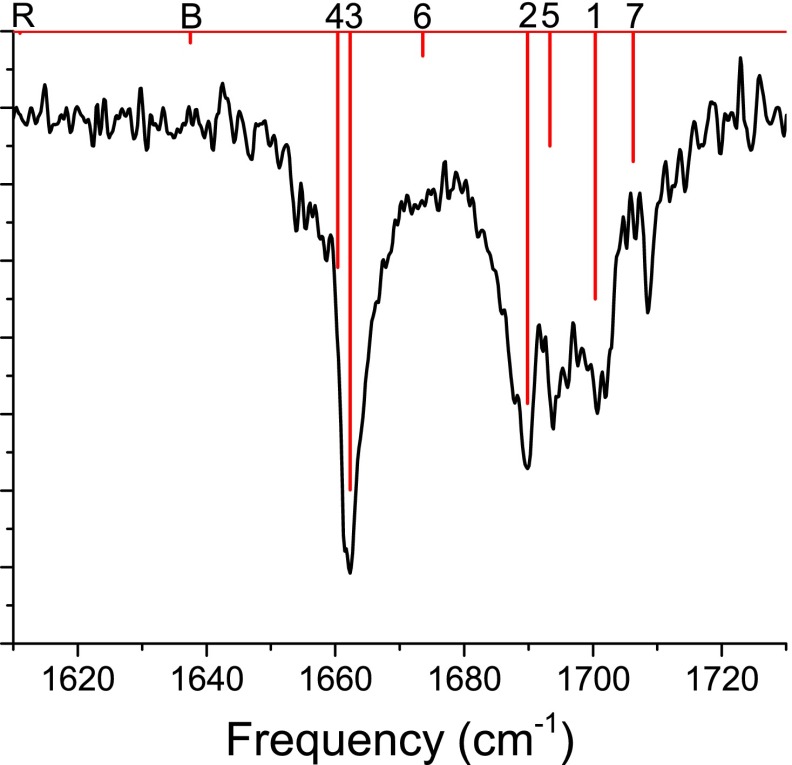
Typically, frequencies obtained from DFT calculations are significantly too high (both because the calculations involve the harmonic approximation, and due to errors in the exchange functional), and it is necessary to scale the results in order to match experiment.^69,70 Here, we choose our scaling factor such that the strongest theoretical peak of the fully unlabeled peptide (labeled “3” in Figure 3) matches the peak frequency in the experimental IR spectrum. The scaling factor thus obtained is 0.970751, and this factor is applied to each frequency in every DFT calculation.

FIG. 3.

Experimental (black) and DFT (red) spectra for fully protonated, unlabeled Ac-FA5K. DFT lines are labeled according to the dominant contributor to the mode; “R” indicates a phenyl ring-breathing mode, “B” indicates a lysine –${\mathrm{NH}}_3^{+}$ bending mode, and 1-7 indicate amide I modes (labeled as in Figure 1).

D. DFT calculation of frequencies and couplings for ¹³C¹⁸O labels

Considering first the single ¹³C¹⁸O labels, the frequency perturbation from the label is significantly larger than the spread in unlabeled frequencies and the vibrational couplings, so the local-mode frequency is essentially uncoupled from the unlabeled band. Therefore, the relevant DFT normal mode is actually a local mode, and we can obtain the local-mode frequency directly from the harmonic analysis.

The calculation of vibrational couplings using DFT is more challenging, and the most rigorous approaches involve either finite difference calculations^22,23 or Hessian matrix reconstruction methods.^23,71,72 Here, we employ a much simpler approach, which is, however, more in keeping with our treatment of the frequencies. For the ¹³C¹⁸O double labels, we assume that the two labeled modes are decoupled from the other modes of the molecule. This means that we can describe these two modes with a 2 × 2 vibrational Hamiltonian. The diagonal elements are the frequencies of the two local modes, ω_i and ω_j; we determine these from calculations on systems with single ¹³C¹⁸O labels. The off-diagonal elements, meanwhile, are (identically) the coupling β_ij, which we would like to obtain. This 2 × 2 Hamiltonian may be diagonalized to determine two eigenfrequencies λ_±

$${\lambda }_{\pm }=\frac{1}{2}({\omega }_i+{\omega }_j)\pm \frac{1}{2}\sqrt{{({\omega }_i-{\omega }_j)}^2+4{\beta }_{ij}^2}.$$ (1)

The eigenfrequencies λ_± are simply the labeled frequencies determined from DFT calculations on a doubly ¹³C¹⁸O-labeled system. We therefore rearrange Eq. (1) to solve for β_ij

$$|{\beta }_{ij}|=\frac{1}{2}{[{({\lambda }_{+}-{\lambda }_{-})}^2-{({\omega }_i-{\omega }_j)}^2]}^{1/2}.$$ (2)

The magnitude of β_ij can thus be determined from the vibrational frequencies of the appropriate singly and doubly isotope-labeled systems. The sign of β_ij can then be determined by making use of the known dependence of the intensities of the transitions for the two eigenfrequencies (which come from the DFT calculation) on the angle between the transition dipoles and the sign of β_ij (analysis not presented).⁷³

E. Map-based calculation of frequencies and couplings for ¹³C¹⁸O labels

For a given peptide configuration (in this case the DFT-optimized configuration of Ac-FA5K), the maps provide a prescription for the local-mode frequencies and couplings.^14,31–33 For the frequencies, several components must be considered. The first involves the electrostatic environment of a given amide I vibration, including (in general) the solvent (water or lipid), ions, and peptide residues that are not nearest neighbors of the residue of interest. In this case, of course, solvent and ions are absent, so the electrostatic contribution comes only from peptide atoms. In our map, the frequency of a single chromophore is determined by the electric fields (due to the other peptide atoms) on the C and N atoms of the amide of interest (in the CO direction).¹⁴ Specifically, the electric fields considered are those created by the atomic charges that would be present in a GROMOS96 53a6 simulation.³⁴ Note that although GROMOS96 53a6 treats aliphatic CH, CH₂, and CH₃ groups as united atoms, the united atoms are always uncharged, so contributions from these groups to the frequency are not considered.

The frequency maps have a zero-field intercept, which was parameterized to be 1684 cm⁻¹ from experimental line-shape data for NMAD in D₂O, DMSO, and chloroform. This differs from the gas-phase frequency for the amide I mode of NMAD, 1717 cm⁻¹,⁷⁴ and accounts for general solvation effects. Indeed, we estimate that the frequency of NMAD in hexane and other non-polar solvents would be close to this lower value.^14,75–77 These solvation effects are not relevant for the present application to a gas-phase peptide; in this work, therefore, we modify our map by shifting the intercept back to the gas-phase value of 1717 cm⁻¹. In addition, however, the ¹³C¹⁸O isotope label produces a shift of −70 cm⁻¹,^14,31,32 reducing the intercept to 1647 cm⁻¹. Therefore, the map we use for these isotope labels is

$$\omega =1647+7729E_C-3576E_N,$$ (3)

where the frequency is in cm⁻¹ and the electric fields E_C and E_N are in atomic units.

In the calculation of the electric fields for the map just presented, the contributions from the C, O, N, H, and alpha-C atoms of the chromophore of interest and of any neighboring amide groups are excluded. These contributions are handled by computing a nearest-neighbor frequency shift, which is added to the result from Eq. (3), using a map created by Jansen and co-workers.¹⁰ In this map, which was parameterized based on DFT calculations (at the RPBE/TZ2P level^78–80) for N-acetyl-glycine-N′methylamide (a 2-chromophore glycine dipeptide), the frequency shift due to a neighboring amide group is parameterized as a function of the Ramachandran angles between the two residues. Different parameterizations are provided for neighboring residues on the C- and N-sides of the amide I of interest.^10,81

For the coupling between pairs of amide I chromophores, we adopt strategies developed by others.^10,22 Couplings between neighboring amide groups are determined by DFT calculations on glycine dipeptide and are parameterized in terms of the Ramachandran angles between the amides.¹⁰ For couplings between non-nearest-neighbor amides, the transition dipole coupling model of Torii and Tasumi²² is employed. This model, which was parameterized using calculations at the HF/6-31+G** level^82,83 for glycine dipeptide, computes couplings using transition-dipole interactions

$${\beta }_{ij}=383\frac{{\widehat{u}}_i·{\widehat{u}}_j-3\left[({\widehat{u}}_i·{\widehat{n}}_{ij})({\widehat{u}}_j·{\widehat{n}}_{ij})\right]}{r_{ij}^3},$$ (4)

where ${\widehat{u}}_i$ is the transition dipole unit vector for the ith chromophore, ${\widehat{n}}_{ij}$ is the unit vector pointing from dipole i to dipole j, and r_ij is the distance between the dipoles (in Å). The conversion factor produces a coupling in cm⁻¹.¹⁴ The location of the transition dipole is given by ${\vec{r}}_C+(0.665$ Å$){\widehat{n}}_{CO}$ + (0.258 Å$){\widehat{n}}_{CN}$, where ${\vec{r}}_C$ is the position of the amide C, and ${\widehat{n}}_{CO}$ and ${\widehat{n}}_{CN}$ are unit vectors pointing from the amide C to the amide O and N, respectively. The dipole lies in the CON plane and forms an angle of 10° with the OC vector; this geometry is displayed in Figure 2.

FIG. 2.

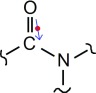
Diagram of amide I transition dipole position and orientation. The position of the dipole is the red dot. The dipole vector lies in the CON plane and forms an angle of 10° with the OC vector.

III. RESULTS AND DISCUSSION

A. Comparison of experimental and DFT spectra

In Figure 3, we display experimental and DFT results for the spectrum of the unlabeled peptide. The DFT and experimental results are found to agree very well; frequencies are accurate to within a few cm⁻¹, and intensities compare reasonably to experiment. Line “R,” which appears at 1611 cm⁻¹, is a phenyl ring-breathing (concerted C–C stretching) mode. Line “B,” which appears at 1638 cm⁻¹, is a bending mode of the lysine –${\mathrm{NH}}_3^{+}$ side chain. The other lines are from amide I modes and are labeled 1–7 according to the local mode (numbered as in Figure 1) that primarily contributes to the normal mode. The fractional contribution of each local mode to the normal mode is determined by

$$f_i=\frac{m_{Ci}|{\vec{r}}_{Ci}{|}^2+m_O{\left|{\vec{r}}_{Oi}\right|}^2}{{\sum }_{j=1}^7(m_{Cj}|{\vec{r}}_{Cj}{|}^2+m_O|{\vec{r}}_{Oj}{|}^2)},$$ (5)

where m_Ci and m_O are the masses of the C and O atoms of the ith amide group (because of ¹³C labeling, the carbon mass can vary), and ${\vec{r}}_{Ci}$ and ${\vec{r}}_{Oi}$ are the Cartesian normal-mode displacements (output by Gaussian) for the C and O atoms of the ith amide group. Despite significant normal-mode delocalization, the labeling scheme is unambiguous.

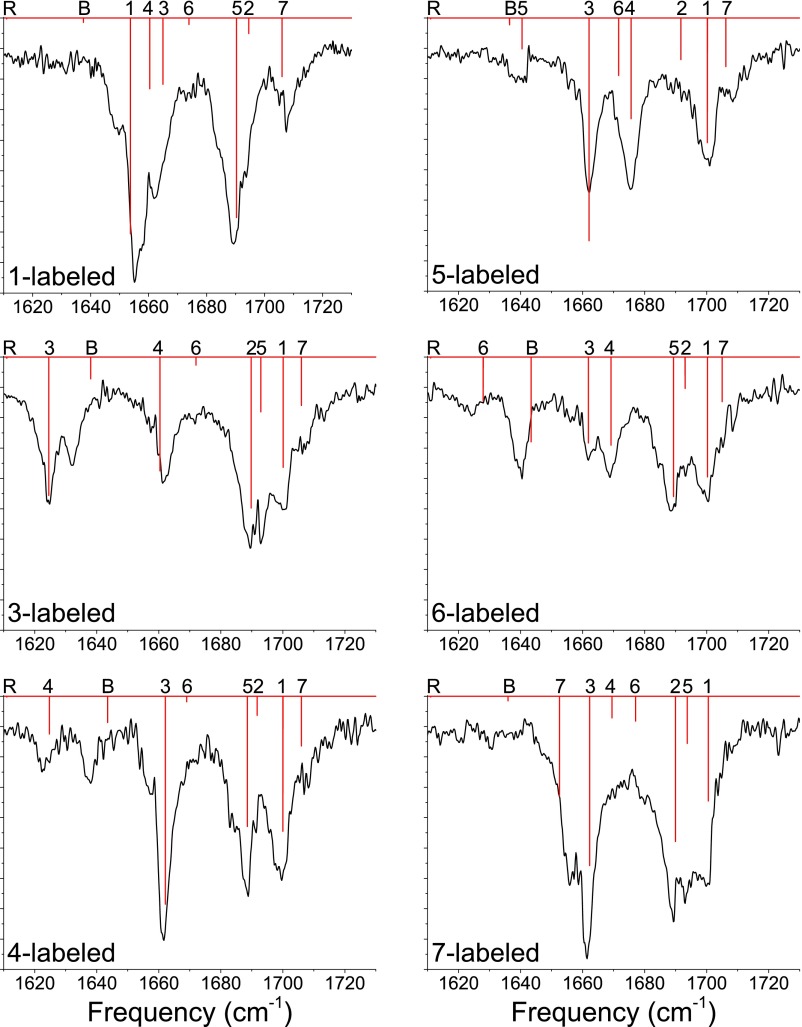
In Figure 4, we display experimental and DFT results for peptides with single ¹³C labels at the specified positions. With single labels, an amide I local mode can be isolated somewhat from the other amide I modes, allowing us to examine the ability of DFT to treat the frequency of an isolated chromophore and to reproduce changes in the other amide modes upon shifting this frequency.^84–86 Again, the DFT results are very good. The greatest errors are observed for the bending mode and for the ¹³C-labeled mode 6, which couples significantly to the bend; this indicates that the scaling factor applied to the DFT frequencies does not work as well for the bend as for the pure amide I modes. (This is to be expected, as the anharmonicities of the amide I and lysine bending modes should differ significantly.) These flaws notwithstanding, the modes generally appear at frequencies consistent with experiment, indicating that DFT characterizes the amide I modes quite well.

FIG. 4.

Experimental (black) and DFT (red) spectra for fully protonated, singly ¹³C-labeled Ac-FA5K. DFT lines are labeled according to the dominant contributor to the mode; “R” indicates a phenyl ring-breathing mode, “B” indicates a lysine –${\mathrm{NH}}_3^{+}$ bending mode, and 1-7 indicate amide I modes (labeled as in Figure 1).

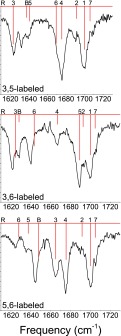
In Figure 5, we display experimental and DFT results for peptides with double ¹³C labels at the specified positions. Double labels are particularly useful for probing the coupling between a pair of labeled chromophores in relative isolation from the other amide modes.^33,35,85 The results are of comparable quality to the unlabeled and single-labeled results; the lysine bending mode and labeled modes with significant bend character appear at somewhat too high a frequency, but the results are otherwise very good. Taken together, the results in Figures 3–5 convince us that DFT calculations at the B3LYP/6-31G** level accurately treat the amide I modes of Ac-FA5K. Moreover, these results strongly support the validity of the structural assignment of the conformer studied here, which was based on a comparison of experimental and DFT NH-stretch spectra.⁵¹

FIG. 5.

Experimental (black) and DFT (red) spectra for fully protonated, doubly ¹³C-labeled Ac-FA5K. DFT lines are labeled according to the dominant contributor to the mode; “R” indicates a phenyl ring-breathing mode, “B” indicates a lysine –${\mathrm{NH}}_3^{+}$ bending mode, and 1-7 indicate amide I modes (labeled as in Figure 1).

B. Assessment of spectroscopic maps

In assessing our maps, it is more interesting from a theoretical point of view to assess the ingredients of the map, rather than the results of the map. In other words, the one-exciton Hamiltonian for the amide I vibrations has diagonal elements (the local-mode frequencies) and off-diagonal elements (the couplings between pairs of local modes). These are the ingredients of the map, and we use a variety of strategies to obtain these matrix elements. It is important, then, to assess our approaches for these matrix elements. In contrast, an assessment of the eigenfrequencies which result from the matrix elements provides less insight into how well different parts of the map work, and how the map might be improved.

The most obvious way to assess the diagonal and off-diagonal matrix elements is through isotope substitution, as discussed above. Ideally, we could use the experimental results for singly and doubly ¹³C-labeled peptides to determine frequencies and couplings and compare them with our maps. However, there are two problems with this approach: (1) the maps were developed for deuterated amide I modes whereas the experiments were performed using fully protonated peptides (for which the amide modes are slightly shifted and coupled to the lysine bend), and (2) the ¹³C labels used experimentally, with their ∼40 cm⁻¹ frequency shift, do not fully decouple every labeled mode (i.e., do not move every frequency far enough outside the unlabeled band). Moreover, all possible single and double labels were not studied experimentally.

The fact that the DFT calculations do an excellent job of reproducing the experimental spectra for the unlabeled and ¹³C-labeled peptides suggests an alternative strategy: rather than assessing the map by comparing to experiment, we can instead compare to DFT calculations. For these calculations, we use ¹³C¹⁸O labels. ¹³C¹⁸O labels induce a frequency shift of ∼70 cm⁻¹, which decouples the labeled and unlabeled modes much better than the 40 cm⁻¹ shift of ¹³C labels. Additionally, we consider all possible singly and doubly labeled peptides.

In Table I, we compare the seven ¹³C¹⁸O-labeled frequencies from B3LYP/6-31G** calculations (for the peptide deuterated at all amides and at the lysine amine) and the map. The mean unsigned error is 3.5 cm⁻¹, and the mean signed error is −1.8 cm⁻¹; if chromophores 1 and 7 are excluded, the mean unsigned error is 1.8 cm⁻¹, and the mean signed error is 0.6 cm⁻¹. Given that the frequency variation among chromophores is about 35 cm⁻¹, these errors are quite small, especially if the terminal chromophores are excluded. The better results for residues in the middle of the chain may reflect a cancellation of errors between the N-side and C-side nearest-neighbor frequency shifts.¹⁰ Possibly, the maps for the terminal residues ought to be parameterized separately.

Table I.

Comparison of ¹³C¹⁸O-labeled frequencies between DFT (B3LYP/6-31G**) and the spectroscopic map. Chromophore numbers are as in Figure 1.

Labeled chromophore	DFT frequency (cm−1)	Map frequency (cm−1)
1	1618.1	1607.2
2	1615.1	1612.8
3	1589.0	1591.2
4	1590.4	1593.9
5	1601.2	1601.5
6	1586.5	1585.7
7	1621.4	1616.7

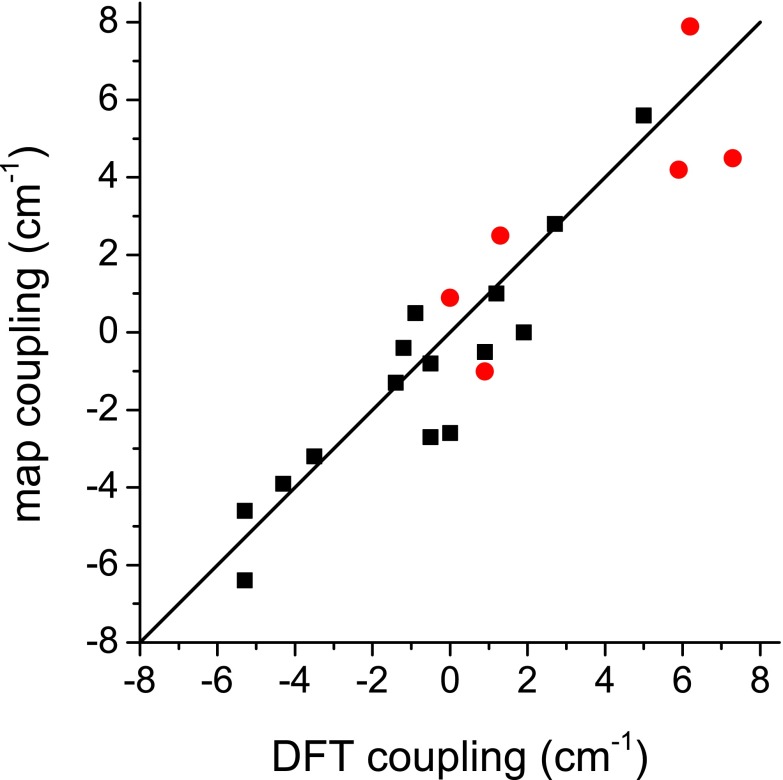
The couplings between nearest-neighbor chromophores are shown in Table II. Recall that the map values come from the nearest-neighbor coupling map,¹⁰ while the DFT values are calculated using the method presented in Subsection II D. The mean unsigned error is 1.7 cm⁻¹, and the mean signed error is −0.4 cm⁻¹. The couplings for all other chromophore pairs are shown in Table III. Here, the map values are approximated using transition dipole coupling.²² The mean unsigned error is 0.9 cm⁻¹, and the mean signed error is −0.4 cm⁻¹. We also present the data in Tables II and III graphically in Figure 6. Thus, we see that the couplings are fairly well reproduced, particularly when transition dipole coupling is used (for non-nearest-neighbors).

Table II.

Comparison of nearest-neighbor couplings between DFT (B3LYP/6-31G**) and the spectroscopic map. Chromophore numbers are as in Figure 1.

Labeled chromophores	DFT coupling (cm−1)	Map coupling (cm−1)
1,2	1.3	2.5
2,3	0.0	0.9
3,4	0.9	−1.0
4,5	5.9	4.2
5,6	6.2	7.9
6,7	7.3	4.5

Table III.

Comparison of non-nearest-neighbor (transition-dipole) couplings between DFT (B3LYP/6-31G**) and the spectroscopic map. Chromophore numbers are as in Figure 1.

Labeled chromophores	DFT coupling (cm−1)	Map coupling (cm−1)
1,3	−5.3	−4.6
1,4	−0.5	−2.7
1,5	−0.5	−0.8
1,6	−1.2	−0.4
1,7	1.2	1.0
2,4	−4.3	−3.9
2,5	0.0	−2.6
2,6	0.9	−0.5
2,7	−0.9	0.5
3,5	−3.5	−3.2
3,6	−5.3	−6.4
3,7	1.9	0.0
4,6	2.7	2.8
4,7	5.0	5.6
5,7	−1.4	−1.3

FIG. 6.

Plot depicting correlation between DFT and map couplings. Black squares are for non-nearest neighbors, and red circles are for nearest neighbors. DFT couplings are calculated as described in Subsection II D. Non-nearest-neighbor couplings are calculated using Torii and Tasumi's²² TDC map. Nearest-neighbor couplings are calculated using Jansen and co-workers’¹⁰ Ramachandran angle-based map.

IV. CONCLUSIONS

In this work, we have used a combination of IR-UV double-resonance spectroscopy and DFT calculations (at the B3LYP/6-31G** level) to evaluate the accuracy of our spectroscopic maps for the amide I vibrations of peptides. The DFT results for the unlabeled peptide, and for peptides with various single and double ¹³C labels, are in excellent agreement with experiment. This gives us confidence to use similar DFT calculations on deuterated and ¹³C¹⁸O-labeled peptides in order to assess our spectroscopic maps. We find that for the seven-chromophore alpha-helical peptide examined here, the maps are accurate to within a few cm⁻¹ for both frequencies and couplings.

The frequency map works very well indeed for chromophores in the interior of the chain, but works less well for terminal chromophores. This suggests that it might be worth developing separate parameterizations for terminal chromophores. For non-nearest-neighbor couplings, a transition-dipole scheme, unmodified from that developed by Torii and Tasumi²² 15 years ago, works remarkably well, in agreement with a recent collaboration with the Zanni group.³³ Nearest-neighbor couplings are described slightly less well (albeit still reasonably) by the map,¹⁰ and there may be room for further improvement in this area.

Another way to extend these maps would be to treat explicitly non-polar effects (particularly dispersive interactions), which are presently handled by the zero-field intercept of the frequency map. For the gas-phase peptide studied here, we set that intercept to the gas-phase frequency of the NMAD chromophore, whereas for applications to proteins in water or lipids, we use a value parameterized from spectra in different solvents.¹⁴ It would be desirable, however, to use the gas-phase intercept in all cases, and employ additional (non-electrostatic) mapping variables to decrease the frequency for solvated peptides. A method along these lines has recently been suggested by Małolepsza and Straub,⁸⁷ whose frequency map mirrors ours but includes additional shifts due to van der Waals forces on the atoms of the amide group. Although the frequency intercept of this map is still much lower than the gas-phase value (∼1675 cm⁻¹), this work is an intriguing contribution.

One noteworthy observation concerning these results is that the electrostatic map seems to work fairly well for a situation with point charges from protein atoms only (and not solvent). Because the map was parameterized for NMAD in three solvents (and therefore did not include any electric fields from protein point charges in the parameterization), it was not entirely obvious that the map would work well for the GROMOS protein point charges (although we have accumulated a reasonable body of work suggesting that it does^14,31–33). We note, however, that in work not presented here, we found the map to work poorly when using point charges from the CHARMM force field,⁸⁸ indicating that it is important to use a map with the force field for which it was parameterized. (The protein force field may affect the electric field map parameters through the sampling of NMAD/solvent conformations, or through the different solvent models required for different force fields.)

In summary, although there is certainly more work to be done, the present results indicate that the error intrinsic to the frequency and coupling maps is quite small (a few cm⁻¹) in most cases, assuming that solvation conditions are properly accounted for. (Recall that it was necessary to shift the zero-field intercept of the frequency map from 1684 cm⁻¹, the original parameter for a well-solvated peptide,¹⁴ to 1717 cm⁻¹, the appropriate value for a gas-phase peptide.⁷⁴) Although we have only examined an α-helical structure in this work, our similar results for a β-sheet structure in a previous study³³ suggest that this result may be general for a variety of secondary structures. Accordingly, to the extent that larger errors are seen when comparing experimental and theoretical spectra for more complex systems, it is likely that improper configurational sampling (possibly due to inadequate force fields) is to blame, rather than the effectiveness of the maps.