Abstract
Most complex human diseases are likely the consequence of the joint actions of genetic and environmental factors. Identification of gene-environment (GxE) interactions not only contributes to a better understanding of the disease mechanisms, but also improves disease risk prediction and targeted intervention. In contrast to the large number of genetic susceptibility loci discovered by genome-wide association studies, there have been very few successes in identifying GxE interactions which may be partly due to limited statistical power and inaccurately measured exposures. While existing statistical methods only consider interactions between genes and static environmental exposures, many environmental/lifestyle factors, such as air pollution and diet, change over time, and cannot be accurately captured at one measurement time point or by simply categorizing into static exposure categories. There is a dearth of statistical methods for detecting gene by time-varying environmental exposure interactions. Here we propose a powerful functional logistic regression (FLR) approach to model the time-varying effect of longitudinal environmental exposure and its interaction with genetic factors on disease risk. Capitalizing on the powerful functional data analysis framework, our proposed FLR model is capable of accommodating longitudinal exposures measured at irregular time points and contaminated by measurement errors, commonly encountered in observational studies. We use extensive simulations to show that the proposed method can control the Type I error and is more powerful than alternative ad hoc methods. We demonstrate the utility of this new method using data from a case-control study of pancreatic cancer to identify the windows of vulnerability of lifetime body mass index on the risk of pancreatic cancer as well as genes which may modify this association.
Keywords: gene-environment interaction, GWAS, functional data analysis, longitudinal exposure, measurement error
Introduction
Most complex human diseases are likely caused by the interplay between genetic and environmental risk factors [Thomas, 2010]. With the rapidly decreasing cost of high-throughput genotyping and next-generation sequencing technology, many large-scale genome-wide association studies (GWAS) and meta-analysis efforts have identified thousands of genetic loci associated with hundreds of human diseases and complex traits [Hindorff et al., 2009]. These findings have provided novel insights into the biological mechanisms of complex disease [Visscher et al., 2012]. Despite the great success of GWAS, a large proportion of the heritability of complex traits remains unexplained, which is often referred to as “missing heritability” [Manolio, 2013; Zuk et al., 2012]. The missing heritability has been attributed to yet to be identified rare genetic variants, gene-gene (GxG) and gene-environment (GxE) interactions. Identification of GxE interactions may contribute to finding the “missing heritability”, provide novel insights into the underlying disease mechanism [Wu et al., 2012], improve disease risk prediction [Garcia-Closas et al., 2013], and help develop disease prevention strategies because environmental exposures, which unlike genetic factors, are often modifiable.
Despite the great promise of GxE interactions, in contrast to the large number of GWAS-identified loci, only a few robustly replicated GxE interactions have been reported in the literature [Hutter et al., 2013; Wu et al., 2012]. The limited success can be attributed to a few challenges facing the GxE investigations. First, while typical GWAS are designed to ensure sufficient power for detecting genetic main effects, straightforward genome-wide scanning of GxE interactions has very limited power [Mukherjee et al., 2012a; Murcray et al., 2011]. In addition to ongoing efforts to increase sample sizes through study consortia collaborations, many new and powerful statistical methods and analysis strategies have been recently proposed to increase the statistical power for detecting genome-wide GxE interactions, including the Empirical Bayes (EB) method [Mukherjee and Chatterjee, 2008], two-stage methods [Kooperberg and Leblanc, 2008; Murcray et al., 2009], hybrid methods [Gauderman et al., 2013; Hsu et al., 2012; Murcray et al., 2011], and biological pathway-based methods [Jiao et al., 2013; Tang et al., 2014a; Tang et al., 2014b], among others [Hutter et al., 2013]. Second, environmental exposures are often not accurately measured. For example, dietary intake data are usually collected from food frequency questionnaires, which can be contaminated by measurement errors [Aschard et al., 2012]. As large collaborative consortia have become the mainstream in genetic epidemiology studies, environmental variables may be measured differently in individual cohorts and thus impose challenges for data harmonization and replication studies [Li et al., 2014]. Third, many environmental exposures are longitudinal and time-varying, e.g., air pollution, toxic exposure and dietary intake, while time-varying exposures in current GxE analysis are often simply treated as static and measured at some arbitrary time point, which may lead to possible bias and loss of power. Although the importance of taking into account time-varying environmental exposures in GxE analysis has been recognized [Bookman et al., 2011; Hutter et al., 2013; Mechanic et al., 2012], almost all statistical methods for GxE analysis, including the aforementioned works, only consider static environmental exposures. A few exceptions include [Ko et al., 2013; Mukherjee et al., 2012b], who proposed novel statistical methods to detect time-varying gene by cumulative environmental exposure interactions for repeatedly-measured quantitative traits in longitudinal cohort studies, i.e., G x E x time interactions.
On the other hand, case-control studies are often embedded in large cohort studies, for example, the Framingham Heart Study [Splansky et al., 2007] and the Kaiser Permanente cohort [Hoffmann et al., 2011], where the past longitudinal exposure data for both cases and controls may be available. Less commonly, as in the case-control study of pancreatic cancer to be analyzed here, lifetime body weight, thus, body mass index (BMI) history was collected retrospectively by personal interview. While considerable efforts have been devoted to modeling the association between longitudinal exposure and disease risk [Bhadra et al., 2012; Pepe et al., 1999; Sanchez et al., 2011], there is a lack of statistical methods to model and detect the interaction between gene and longitudinal environmental exposure in a case-control study.
To help alleviate this gap, we propose a novel statistical method for testing gene by longitudinal environmental exposure in the functional data analysis (FDA) framework. FDA is a powerful tool to extract informative features from high-dimensional longitudinal data, often contaminated by measurement errors, and achieve substantial dimension reduction [Ramsay and Silverman, 2005; Yao et al., 2005]. This technique has been successfully employed in image analysis [Sorensen et al., 2013], time-course gene expression analysis [Leng and Muller, 2006], and statistical genetics to model the association between rare genetic variants and disease phenotype [Luo et al., 2011]. In our proposed new method, we first reduce the dimension of the longitudinal environmental exposure by the functional principle component analysis (FPCA), taking into account measurement errors, and then model gene by longitudinal environmental exposure interaction by the functional logistic regression (FLR) model [Müller, 2005]. The new method is demonstrated by using a pancreatic cancer candidate gene-based case-control study to detect interactions between gene and BMI across an individual’s lifespan. Our real data-based simulation study shows the proposed method can satisfactorily control the Type I error and is more powerful than alternative methods.
Material and Methods
Notations
We consider a case-control study with a total sample size n including n1 cases and n2 controls (n = n1 + n2). Let Di denote the binary disease status of individual i: 0 for controls and 1 for cases (i = 1, .., n). Let Zi denote the covariate vector, including, for example, sex, age, and leading principle components capturing population substructure. Given a SNP to be tested for GxE interaction, let Gi denote the genotype of the SNP in subject i, equal to 0, 1 and 2 for major allele homozygotes, heterozygotes and minor allele homozygotes, respectively. In contrast to traditional GxE analysis in which a static environmental exposure is considered, here for each individual i, we consider time-varying environmental exposure, denoted by Ei(tij), where tij is the time of the individual i’s jth measurement (j = 1, …, Ji) and Ji is the individual i’s total number of measurements. tij takes values in the time interval
 = [T1, T2], which can be rescaled to the unit interval [0,1]. For example, in our pancreatic cancer case-control study example to be detailed later on, tij is the jth age period (in 10-year intervals from age 14–19 years until one year prior to diagnosis for cases or recruitment into the study for frequency-matched controls) in which the individual i’s BMI information was collected. See [Bhadra et al., 2012] for a more complete treatment of the time index tij. Other examples of longitudinal exposures include air pollutant intensity over time, dietary intake over a follow-up period, or lifestyle/host factors such as sex hormone levels and lifetime BMI in the application here. Note that Eis can be measured at either the same or different time points across individuals, the latter of which is more typical in observational studies.
= [T1, T2], which can be rescaled to the unit interval [0,1]. For example, in our pancreatic cancer case-control study example to be detailed later on, tij is the jth age period (in 10-year intervals from age 14–19 years until one year prior to diagnosis for cases or recruitment into the study for frequency-matched controls) in which the individual i’s BMI information was collected. See [Bhadra et al., 2012] for a more complete treatment of the time index tij. Other examples of longitudinal exposures include air pollutant intensity over time, dietary intake over a follow-up period, or lifestyle/host factors such as sex hormone levels and lifetime BMI in the application here. Note that Eis can be measured at either the same or different time points across individuals, the latter of which is more typical in observational studies.
Standard logistic regression for gene by longitudinal environmental exposure interaction
Since the standard logistic regression model can only test the interaction between gene and environmental exposures one at a time, it requires the longitudinal environmental exposures to be measured at the same time points across all n individuals, that is, J1 = J2 = ··· = Jn = J and t1j = t2j = ··· = tnj for all j = 1, …, J. Should this not hold, measurement time points need to be grouped into intervals in an ad hoc way, for example, into 5-year intervals [Sanchez et al., 2011]. Measurements in the same interval are then averaged, leading to a single environmental exposure value for each individual. We re-write Ei(tij) as Eij to denote the individual i’s exposure measure at the jth aligned time point. We fit the following logistic regression model, for j = 1, …, J,
| (1) |
under the additive genetic model. Other alternative genetic models, such as the dominant or recessive model, can also be assumed. We test the null hypothesis H0:βGE,1 = βGE,2 = ··· = βGE,J = 0 against the alternative H1: at least one of βGE,j is not 0. This can be done by calculating a p-value for each βGE,j and taking the minimum of the J p-values, denoted as minP. We then compare minP with the Bonferroni correction significance threshold 0.05/J. Since the J longitudinal exposures Eij’s are likely to be correlated, the Bonferroni correction, which assumes independent multiple tests, tend to be conservative, leading to reduced statistical power. Alternatively, we can resort to the parametric bootstrap method to obtain the null distribution of minP taking into account correlated measurements [Buzkova et al., 2011].
In the standard logistic regression framework, we can also model the longitudinal exposures jointly via
| (2) |
We test the null hypothesis H0:βGE,1 = βGE,2 = ··· = βGE,J = 0 against the alternative H1: at least one of βGE,j is not 0. This seems to be the same as that in Model (1); however, the key difference is that βE,j and βGE,j in Equation (1) are estimated for each environmental exposure measurement separately, whereas those in Equation (2) are estimated jointly for all measurements. We can employ a J-degrees-of-freedom likelihood ratio test (LRT), or its asymptotically equivalent score and Wald tests, to test the above hypothesis, which may suffer from loss of power if the number of measurements J is large [Pan et al., 2011]. Another caveat of Model (2) is that correlated longitudinal exposures may lead to unstable numerical solutions due to multicollinearity.
New method: functional logistic regression and FPCA
The FDA, including the FPCA and functional linear/generalized linear models, has emerged as a powerful approach to modeling noisy and irregularly measured longitudinal data in association with a scalar response variable, e.g., disease outcome [Li et al., 2010; Müller, 2005]. Here we propose to model the longitudinal environmental exposure in the FDA framework. First we decompose the longitudinal exposure trajectory into a few uncorrelated components using the FPCA, taking into account possible measurement errors, and then model gene by longitudinal exposure interaction using the functional logistic regression (FLR) model.
FPCA
We model the n individuals’ exposure trajectories as independent realizations from a square integrable stochastic process {E(t), t ∈
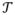 } with mean function μ(t) and covariance function R(s, t) = cov{E(s), E(t)} in time domain s, t ∈
} with mean function μ(t) and covariance function R(s, t) = cov{E(s), E(t)} in time domain s, t ∈
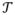 = [T1, T2]. By Mercer’s Thorem [Leng and Muller, 2006], we have eigendecomposition
, where ρk and λk are eigenfunctions and eigenvalues ordered by size λ1 ≥ λ2 ≥ ···. The orthonormal eigenfunctions satisfy
= [T1, T2]. By Mercer’s Thorem [Leng and Muller, 2006], we have eigendecomposition
, where ρk and λk are eigenfunctions and eigenvalues ordered by size λ1 ≥ λ2 ≥ ···. The orthonormal eigenfunctions satisfy
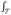 ρj(t)ρl(t) dt = δjl, which is 1 if j = l and 0 otherwise. By the Karhunen–Loève decomposition [Yao et al., 2005], a random curve Ei(t) from the population can be represented by
ρj(t)ρl(t) dt = δjl, which is 1 if j = l and 0 otherwise. By the Karhunen–Loève decomposition [Yao et al., 2005], a random curve Ei(t) from the population can be represented by
| (3) |
where FPCik =
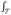 (Ei(t)−μ(t))ρk(t)dt is the kth functional principle component (FPC) score for the ith subject. In addition, FPCik satisfies E(FPCik) = 0 and Var(FPCik) = λk. The value of FPCik measures the similarity between the deviation of individual curve Ei(t) from the population mean and the kth eigenfunction (FPC) ρk(t). The above FPCA framework for functional data is analogous to the representation of random vectors in multivariate analysis by principle components: a random vector can be represented as linear combination of the orthonormal basis defined by the eigenvectors of its covariance matrix, which is the finite-dimensional equivalent of the Karhunen–Loève decomposition.
(Ei(t)−μ(t))ρk(t)dt is the kth functional principle component (FPC) score for the ith subject. In addition, FPCik satisfies E(FPCik) = 0 and Var(FPCik) = λk. The value of FPCik measures the similarity between the deviation of individual curve Ei(t) from the population mean and the kth eigenfunction (FPC) ρk(t). The above FPCA framework for functional data is analogous to the representation of random vectors in multivariate analysis by principle components: a random vector can be represented as linear combination of the orthonormal basis defined by the eigenvectors of its covariance matrix, which is the finite-dimensional equivalent of the Karhunen–Loève decomposition.
We further assume that we observe the ith individual’s exposure trajectory {Ei(tij), j = 1, …, Ji}, contaminated by measurement errors, at Ji time points for i = 1, …, n:
| (4) |
where the measurement error εij, independent of Ei(tij), has mean 0 and variance σ2 following the classical measurement error model [Carroll et al., 2006]. The observation time points tij’s can be either the same across individuals (regular time intervals) or irregular and sparse, the latter of which is often encountered in observational studies.
FPCA by Principle Analysis via Conditional Expectation (PACE)
We propose to employ the PACE method [Yao et al., 2005] to estimate the mean function μ(t), covariance function R(s, t), eigenfunctions ρk(t) and FPC scores FPCik from the entire observed data {Eij, i = 1, .., n and j = 1, …, Ji}, including both cases and controls. The PACE method has been shown to be versatile and powerful when applied to sparse and irregularly measured longitudinal data contaminated with measurement errors, as well as regularly measured longitudinal data with possible missing values [Müller, 2009]. Briefly, the PACE method carries out the FPCA as follows. First, all available measurements {(tij, Eij), i = 1, .., n and j = 1, …, Ji} are pooled to form a scatter plot and the estimate μ̂(t) of the mean function μ̂(t) is obtained by a one-dimensional kernel smoother. Second, the estimated covariance function R̂(s, t), for s, t ∈
 = [T1, T2], is obtained by a two-dimensional kernel smoother with all pairwise products {Eij, − μ̂(tij)}{Eil − μ̂(tij)}, for j ≠ l, as the responses and (tij, til) as the predictors. Third, estimated eigenfunctions ρ̂k(t) and eigenvalues λ̂k are obtained by applying spectral decomposition to the smoothed covariance surface R̂(s, t) after discretization. Because the smoothed R̂(s, t) may no longer be positive definite, only positve eigenvalues are retained [Yao et al., 2005]. Fourth, in contrast to estimating the FPC scores by numerical intergration FPCik =
= [T1, T2], is obtained by a two-dimensional kernel smoother with all pairwise products {Eij, − μ̂(tij)}{Eil − μ̂(tij)}, for j ≠ l, as the responses and (tij, til) as the predictors. Third, estimated eigenfunctions ρ̂k(t) and eigenvalues λ̂k are obtained by applying spectral decomposition to the smoothed covariance surface R̂(s, t) after discretization. Because the smoothed R̂(s, t) may no longer be positive definite, only positve eigenvalues are retained [Yao et al., 2005]. Fourth, in contrast to estimating the FPC scores by numerical intergration FPCik =
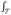 (Ei(t)−μ(t))ρk(t)dt, the PACE method takes measurement errors and sparse measurements into account by assuming FPCik and εij to be jointly normal and predicting the random effects
based on its conditional expectation:
; see [Yao et al., 2005] for details. Predictions
’s are then obtained by plugging in estimates of the parameters from the entire dataset, borrowing information from all subjects. Finally, it is often the case that the infinite-dimensional stochastic process {E(t), t ∈
(Ei(t)−μ(t))ρk(t)dt, the PACE method takes measurement errors and sparse measurements into account by assuming FPCik and εij to be jointly normal and predicting the random effects
based on its conditional expectation:
; see [Yao et al., 2005] for details. Predictions
’s are then obtained by plugging in estimates of the parameters from the entire dataset, borrowing information from all subjects. Finally, it is often the case that the infinite-dimensional stochastic process {E(t), t ∈
 } can be well approximated by the function space spanned by the leading K eigenfunctions, leading to a truncated version of the Karhunen–Loève representation,
} can be well approximated by the function space spanned by the leading K eigenfunctions, leading to a truncated version of the Karhunen–Loève representation,
| (5) |
The choice of K can be based on either the fraction of variance explained (FVE) or some model selection criteria, such as modfied AIC and BIC [Li et al., 2010; Yao et al., 2005]. As demonstrated in Equation (5), the infinite-dimensional trajectory Ei(t) is reduced to K FPC scores for each individual. The PACE method is implemented in the Matlab toolbox and R package “PACE”.
Functional Logistic Regression (FLR)
We first consider modeling the association between the disease status and the longitudinal environmental exposure (BMI in the application here) and then introduce the gene by longitudinal exposure interaction model.
Model the main effect of longitudinal exposure on the disease risk
We assume that the disease status is dependent on the longitudinal exposure via the following FLR model [Müller, 2005],
| (6) |
where β(t) is a time-varying coefficient, implying that a constant unit increase in the longitudinal exposure Ei(t) from time t1 to t2 will increase the odds of disease by , given other covariates Zi are fixed. By the Karhunen–Loève representation, both β(t) and Ei(t) can be expanded by the eigenfunctions and . Without loss of generality, we assume μ(t) ≡ 0, as μ(t) is not subject-specific and can be aborbed to the intercept α0 in model (6). Furthermore, we assume a truncated version of the Karhunen–Loève representation involving only the leading K as in equation (5). From the orthonormality of the eigenfunctions ρk, it follows that Model (6) is equivalent to
| (7) |
i.e., the outcome is dependent only on the leading K FPC scores, which are uncorrelated random effects by construction. We thus propose to: first, apply the PACE method to obtain the estimated and ; second, plug in the estimated FPC scores in Model (7) and estimate the regression coefficeints βk as usual logistic regression; and third, obtain the esitmate of the time varying coefficient β(t) by . We can perform a global test of H0:β1 = β2 = ··· = βK = 0, via, for example, a K-df LRT, to investigate if there is an overall association between the longitudinal exposure and disease risk. To take into account the uncertainty in the estimated FPC scores in Model (7), we can employ the nonparametric bootstrap procedure to obtain the standard error (SE) for the regression coefficients βk’s by resampling the paired observations (Di, Zi, Ei1, …, EiJi)′ with replacement and repeating the PACE procedure and the FLR [Li et al., 2010].
Model the interaction between gene and longitudinal exposure
To model the interaction between a SNP and the longitudinal exposure, we propose the following FLR model,
| (8) |
where β(t) and βGE(t) are time-varying coefficients for the longitudinal exposure main effect and its interaction effect with the SNP G. Similarly to Model (6), we can decompose β(t), βGE(t) and Ei(t) using the leading K orthornormal eigenfunctions ρk and rewrite Model (8) as
| (9) |
Testing the null hypothesis that there is no gene by longitudinal exposure interaction amounts to testing the time-varying interaction coefficient in Model (8) to be 0, i.e., H0:βGE(t) ≡ 0 for any t ∈ [T1, T2], which is equivalent to testing H0:βG1 = βG2 = ··· = βGK = 0 in Model (9). The latter can be tested by a K-df LRT or its asymptotically equivalent score or Wald test. However, the LRT may be less powerful if K is large and/or the interaction effect sizes βGk are moderate. Here we propose to employ the Sum of Squared score (SSU) test [Pan, 2009; Pan et al., 2011] to test the global null hypothesis H0:βG1 = βG2 = ··· = βGK = 0. Let UGE = (UG1, …, UGK)′ denote the efficient score vector for the K interaction terms in Model (9), where , p̂i is the fitted probability of Di = 1 from the main-effects logistic regression model, i.e., Model (9) without the interaction terms, and μ̂i,Gk = Ê(Gi * FPCik) is the fitted response value from the linear regression model . The SSU test statistic is defined as the sum of squared elements of the efficient score vector UGE, i.e., , which has an asymptotic null distribution of a mixture of ’s and can be well approximated by a scaled and shifted χ2 distribution [Pan, 2009]. The SSU test has been shown to be equivalent to the permutation-version of Goeman’s variance component score test for a random-effects logistic regression model [Goeman et al., 2006] and is closely related to kernel-machine regression for SNP-set association test [Pan, 2011; Wu et al., 2010]. We adapt the SSU to test pairwise interaction between a SNP and multiple FPCs, in comparison with testing the SNP-set association or interaction between multiple SNPs and an environmental exposure as originally proposed [Pan, 2009; Pan et al., 2011]. As to be shown in the numerical results, the SSU test was found to outperform other alternative tests.
Data application: a case-control study of pancreatic cancer
Pancreatic cancer is the fourth leading cause of cancer-related deaths for both men and women in the US with a 5-year survival rate of 6% [American Cancer Society, 2013]. Known risk factors for pancreatic cancer include cigarette smoking, long term Type 2 diabetes, heavy alcohol consumption and family history. There is increasing evidence that risk of pancreatic cancer is elevated among individuals who are obese or have high body mass index (BMI; weight in kilograms divided by height in meters squared). Specifically, we have previously shown that excess BMI in young adulthood confers a higher risk of pancreatic cancer than weight gain at a later age in a case-control study conducted at The University of Texas MD Anderson Cancer Center during 2004 to 2009 [Li et al., 2009]. Cases were patients with pathologically confirmed pancreatic adenocarcinoma and controls were healthy individuals frequency matched to cases by age, race, and sex. To assess the lifetime BMI influence on pancreatic cancer risk, we collected, by personal interview, height and body weight history of each study participant starting at ages 14 to 19 years and over 10-year intervals progressing to the year prior to recruitment in the study. The BMI for each individual was then calculated as weight in kilograms at each age period divided by adult body height in meters squared. It is of interest to discover genes that modify the association between changing BMI at different age periods and risk of pancreatic cancer, i.e., gene by longitudinal BMI interaction. As pancreatic cancer is a late-onset malignancy with a median age of diagnosis at 71 years of age [American Cancer Society, 2013], we performed gene by longitudinal BMI interaction analysis on 553 cases and 580 controls who were older than 50 at recruitment and had complete BMI information from age 14–19 progressing in 10-year intervals to age 50–59. These individuals were also genotyped for SNPs in susceptibility genes identified in previous GWAS of pancreatic cancer [Amundadottir et al., 2009; Petersen et al., 2010], including ABO, NR5A2 and CLTPM1L-TERT, as well as FTO, an obesity-associated gene [Berndt et al., 2013]. Genotyping was performed on genomic DNA from peripheral blood samples using the Taqman method. The study was approved by the institutional review board of The University of Texas MD Anderson Cancer Center.
To analyze this real dataset, we applied the univariate and multiple logistic regression Models (1) and (2) as well as the proposed FLR Model (9), in addition to some simple ad hoc methods previously proposed in the literature [Bhadra et al., 2012]. Specifically, we summarized the longitudinal BMI as a scalar via the following functions and then used the summary exposure in a standard logistic regression interaction model: (a) taking average over time to create average exposure
(called “aveBMI”), (b) using the maximum exposure over time Ei,max = max1≤j≤Ji
Eij (called “maxBMI”), (c) using the area under the longitudinal exposure curve (AUC) AUCi =
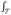 Ei(t)dt (called “aucBMI”), which can be approximated by the trapezoidal rule (see page 122 of [Fitzmaurice et al., 2011]), and (d) the first principle component from multivariate PCA of the longitudinal exposures (called “PC1”). We also considered the leading few PCs explaining at least 95% of the total variation in the observed exposures (called “PC95”). Compared with the proposed FLR Models (8) and (9), the ad hoc models (a) and (c) essentially assumed constant coefficient of the exposure and its interaction with the genetic factor over time, while model (b) assumed that the maximum exposure interacted with the genetic factor in modifying the disease risk regardless when the maximum occurred. These assumptions may not hold in practice, as to be shown in the analysis of the pancreatic cancer example. Also of note, multivariate PCA, including “1stPC” and “PC95”, can only be applied to longitudinal exposures measured at regular time points and cannot accommodate missing values as the FPCA.
Ei(t)dt (called “aucBMI”), which can be approximated by the trapezoidal rule (see page 122 of [Fitzmaurice et al., 2011]), and (d) the first principle component from multivariate PCA of the longitudinal exposures (called “PC1”). We also considered the leading few PCs explaining at least 95% of the total variation in the observed exposures (called “PC95”). Compared with the proposed FLR Models (8) and (9), the ad hoc models (a) and (c) essentially assumed constant coefficient of the exposure and its interaction with the genetic factor over time, while model (b) assumed that the maximum exposure interacted with the genetic factor in modifying the disease risk regardless when the maximum occurred. These assumptions may not hold in practice, as to be shown in the analysis of the pancreatic cancer example. Also of note, multivariate PCA, including “1stPC” and “PC95”, can only be applied to longitudinal exposures measured at regular time points and cannot accommodate missing values as the FPCA.
Results
FPCA of longitudinal BMI
We applied the FPCA to the BMI measures from the following five age intervals with cases and controls pooled together: 14–19, 20–29, 30–39, 40–49 and 50–59 years. We denote the time domain as
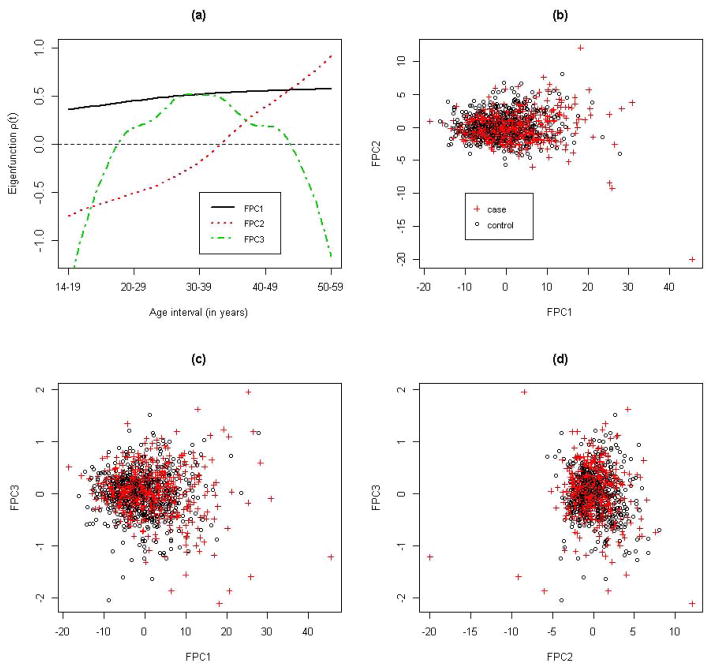
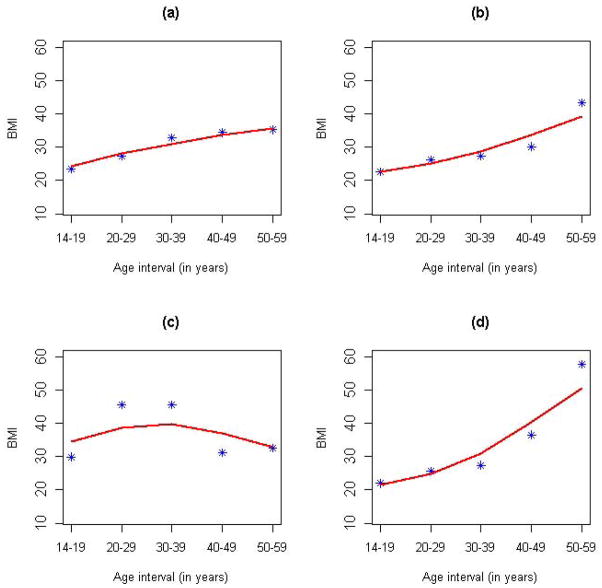
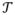 = [T1, T2] = [1, 5], with t = 1, 2, 3, 4 and 5 corresponding to each of the five age intervals. Therefore, the BMI was measured on a regular grid for all individuals: Ji ≡ 5 for all i = 1, .., n, and t1j = t2j = ··· = tnj for all j = 1, …, 5. As shown in Figure S1, the raw BMI profiles exhibited substantial variations in both cases and controls. Taking into account possible measurement errors in the recalled BMI, we employed the PACE method to perform the FPCA of the longitudinal BMI pooled from all cases and controls. The kernel smoothed mean function μ̂(t) and covariance function R̂(s, t) are shown in Figures S2 and S3. The mean function captured the overall increasing trend of BMI with aging, while the covariance function indicated that the covariance between two BMI measures decreased as they became farther away. The PACE method estimated the measure error σ2 to be 1.22, which suggests that the BMI measure was contaminated by a mean zero random error with a standard deviation of 1.2. In addition, the leading three FPCs, i.e., K = 3, were selected by a modified Bayesian Information Criterion (BIC), which is the default model selection method in the PACE package. The top three FPCs explained, respectively, 89%, 9.6% and 1% of the total variation in the observed BMI and explained 99.6% of the total variation collectively (Figure S4). Figure 1 shows the first three FPCs along with scatter plots for pairwise FPC scores. The first FPC represented a relative constant vertical shift from the pooled mean curve. The second FPC captured the pattern of initially underweight and eventually overweight in later adulthood, while the third FPC represented overweight in the middle three age intervals (20–29, 30–39 and 40–49 years). Although the majority of the cases and controls were not obviously separated by the first three FPC scores, there were a number of cases with extreme scores, suggesting that the FPCs might extract useful information regarding the disease risk. We also plotted a few randomly selected individuals’ observed versus PACE predicted (Equation 5) BMI trajectories, as well as for individuals with extreme FPC scores (Figure 2 and S5). We can see that the PACE method predicted the BMI trajectories very well in general and shrunk extreme BMI values toward the population mean for more stable predictions, especially for those individuals with extreme FPC scores (Figure 2(c) and (d) and Figure S5(c) and (d)). On the other hand, as demonstrated in Figure 2(c) and (d), the two individuals with the largest FPC3 and FPC2 score, respectively, matched the corresponding FPCs in Figure 1(a) very well.
= [T1, T2] = [1, 5], with t = 1, 2, 3, 4 and 5 corresponding to each of the five age intervals. Therefore, the BMI was measured on a regular grid for all individuals: Ji ≡ 5 for all i = 1, .., n, and t1j = t2j = ··· = tnj for all j = 1, …, 5. As shown in Figure S1, the raw BMI profiles exhibited substantial variations in both cases and controls. Taking into account possible measurement errors in the recalled BMI, we employed the PACE method to perform the FPCA of the longitudinal BMI pooled from all cases and controls. The kernel smoothed mean function μ̂(t) and covariance function R̂(s, t) are shown in Figures S2 and S3. The mean function captured the overall increasing trend of BMI with aging, while the covariance function indicated that the covariance between two BMI measures decreased as they became farther away. The PACE method estimated the measure error σ2 to be 1.22, which suggests that the BMI measure was contaminated by a mean zero random error with a standard deviation of 1.2. In addition, the leading three FPCs, i.e., K = 3, were selected by a modified Bayesian Information Criterion (BIC), which is the default model selection method in the PACE package. The top three FPCs explained, respectively, 89%, 9.6% and 1% of the total variation in the observed BMI and explained 99.6% of the total variation collectively (Figure S4). Figure 1 shows the first three FPCs along with scatter plots for pairwise FPC scores. The first FPC represented a relative constant vertical shift from the pooled mean curve. The second FPC captured the pattern of initially underweight and eventually overweight in later adulthood, while the third FPC represented overweight in the middle three age intervals (20–29, 30–39 and 40–49 years). Although the majority of the cases and controls were not obviously separated by the first three FPC scores, there were a number of cases with extreme scores, suggesting that the FPCs might extract useful information regarding the disease risk. We also plotted a few randomly selected individuals’ observed versus PACE predicted (Equation 5) BMI trajectories, as well as for individuals with extreme FPC scores (Figure 2 and S5). We can see that the PACE method predicted the BMI trajectories very well in general and shrunk extreme BMI values toward the population mean for more stable predictions, especially for those individuals with extreme FPC scores (Figure 2(c) and (d) and Figure S5(c) and (d)). On the other hand, as demonstrated in Figure 2(c) and (d), the two individuals with the largest FPC3 and FPC2 score, respectively, matched the corresponding FPCs in Figure 1(a) very well.
Figure 1. Functional principle components (FPCs) and FPC scores.
Panel (a) displays the leading three FPCs; panels (b) (c) and (d) display pairwise FPC scores with circles and crosses corresponding to controls and cases, respectively.
Figure 2. Observed versus PACE-predicted BMI profiles.
Panels (a) and (b) display the BMI profiles of two randomly selected individuals with asterisks and solid lines corresponding to observed and PACE-predicted BMI, respectively. Panel (c) shows an individual with the largest FPC3 score and the third smallest FPC2 score. Panel (d) shows an individual with the largest FPC2 score and the smallest FPC3 score.
Modeling the main effect of longitudinal BMI on disease risk by FLR
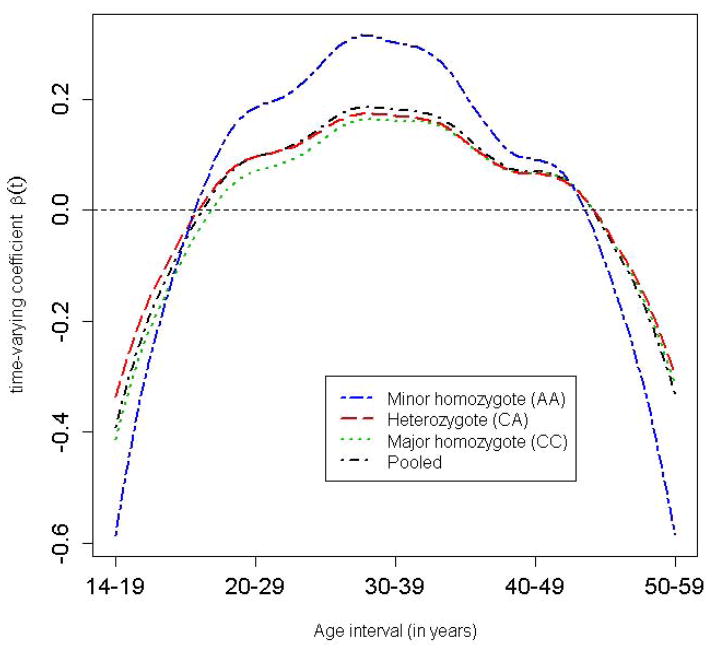
We first investigated the main effect of lifetime BMI on the pancreatic cancer risk via the FLR (Model 6). By resorting to the FPCA procedure as described above, we fitted Model (7) as a usual logistic regression with the predicted FPC scores as covariates adjusted for age at recruitment and gender. Table S1 shows the estimated regression coefficients, their model-based standard errors (SEs)/95% confidence intervals (CIs), as well as bootstrap-based SEs and 95% CIs taking into account the uncertainty in predicting the random FPC scores. It is noted that the model- and bootstrap-based SEs were almost identical, as were the 95% CIs, suggesting that the estimation error was likely ignorable in this data example. The first and third FPCs were both significantly and positively associated with the disease risk (p-value = 1.39 x 10−9 and 0.048, respectively). The p-value for the LRT of the global null hypothesis H0: β1 = β2 = β3 = 0 was 1.55 x 10−9, indicating that the longitudinal BMI was highly significantly associated with the pancreatic cancer risk. Figure 3 shows the time-varying coefficient for the longitudinal BMI obtained by , confirming our previous finding that overweight in the age intervals 20–29 and 30–39 years conferred a higher risk of pancreatic cancer than did weight gain at later ages [Li et al., 2009] (the “pooled” curve corresponds to the BMI main effect; other curves to be discussed in the next section). We can estimate the increase in disease odds for a constant unit increase in the BMI from time t1 to t2 by exponentiating the area under the curve , i.e, . For example, if an individual’s BMI increased by 1 unit from age 25 to 35 years given the BMI during other ages was fixed, the odds of developing pancreatic cancer would increase by approximately 12%. We have demonstrated here that the FLR coupled with FPCA is a powerful means to identify the windows of vulnerability of longitudinal exposure on the disease risk [Hutter et al., 2013].
Figure 3. Genotype-specific time-varying coefficient for the longitudinal BMI.
The individual curves were obtained by fitting Model (7) stratified by the genotype of FTO SNP rs8050136 adjusted for age and gender, while the “pooled” curve was obtained by fitting Model (7) to all the individuals adjusted for age and gender.
Detecting gene by longitudinal BMI interaction by FLR
To identify genes that may modify the association between longitudinal BMI and pancreatic cancer risk, i.e., gene by longitudinal BMI interaction, we applied the FLR interaction Model (9) to SNPs from the candidate gene study of pancreatic cancer. We performed a variety of interaction tests, including FLR-based tests and SNP by age-specific BMI interaction tests, as specified in Models (1) and (2). As shown in Table 1, SNP rs8050136 in FTO was found to be nominally interacting with the longitudinal BMI (p-value for the FLR-based SSU test = 0.02). Age-specific BMI interaction tests showed that the age interval 20–29 years had the smallest p-value = 0.02; however, after adjusting for multiple comparisons, i.e., testing five age-specific BMI interactions in total, the SNP by BMI interaction was no longer significant with the parametric-bootstrap-based minP p-value = 0.14. Noticeably, the interaction test for rs8050136 by BMI for the last age interval, i.e., 50–59 years, was the least significant interval (p-value = 0.12), underscoring the importance of considering longitudinal/lifespan environmental exposure in GxE analysis. SNP rs8050136 together with other SNPs in the FTO gene has been robustly associated with BMI/obesity in previous GWAS [Berndt et al., 2013]. Table S2 shows the regression coefficient estimates in the FLR Model (9) for rs805013; only the first FPC appeared to interact with the SNP (p-value = 0.02). The FLR-based SSU test for the global null hypothesis H0: βG1 = βG2 = βG3 = 0 detected this significant interaction (p-value=0.02), while the FLR-based score test had a non-significant p-value = 0.10 (Table 1). Our simulation study showed that the SSU test was more powerful than the generic LRT and score test while maintaining the Type I error at the nominal level (to be discussed in the next section). In addition, in a previous study of the same population with a larger sample size of 1,000 case-control pairs of pancreatic cancer, we identified a highly significant interaction between rs8050136 and dichotomized adult BMI (age interval 30–39 years), thereby supporting our findings reported here [Tang et al., 2011]. Similar to the main-effect FLR for the longitudinal BMI, the model-based SEs and 95% CIs in the FLR-based interaction model were very close to those based on bootstrapping the “pair” of observations, i.e., the pair of disease status and covariates vector, confirming that the estimation error in the PACE-based FPCA was ignorable in this data example. To further investigate the interaction, we fitted the longitudinal BMI main-effect FLR Model (7) stratified by the genotype of rs8050136 and obtained genotype-specific time-varying coefficients for BMI. As shown in Figure 3, the gene by longitudinal BMI interaction mainly occurred in early adulthood, i.e., ages 20–29 and 30–39 years, consistent with the results from the age-specific BMI interaction analysis (Table 1). For example, for the same 1 unit increase in BMI from age 25 to 35 years, homozygous minor allele carriers of rs8050136 (AA genotype) had approximately 7% higher odds of developing pancreatic cancer than homozygous major allele carriers (CC genotype).
Table 1.
P-values for gene by longitudinal BMI interaction
| SNP | Positionb | Gene | BMIc (14– 19 yrs.) |
BMI (20– 29 yrs.) |
BMI (30– 39 yrs.) |
BMI (40– 49 yrs.) |
BMI (50– 59 yrs.) |
BMId (Bonf. ) |
BMIe (MinP; boot) |
ave BMIf |
max BMIf |
auc BMIf |
PC1g | PC95g | BMIh (Score ) |
FLRi (Score ) |
FLRi (SSU ) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| rs505922 | chr9: 136149229 | ABO | .63a | .28 | .87 | .82 | .67 | 1.0 | .83 | .84 | .66 | .80 | .79 | .53 | .42 | .61 | .77 |
| rs1558902 | chr16: 53803574 | FTO | .11 | .14 | .72 | .33 | .99 | .55 | .46 | .40 | .97 | .38 | .35 | .38 | .06 | .39 | .36 |
| rs8050136 | chr16: 53816275 | FTO | .04 | .02 | .04 | .03 | .12 | .12 | .14 | .03 | .09 | .03 | .03 | .11 | .17 | .10 | .02 |
| rs1202940 | chr1: 199905828 | NR5A 2 | .69 | .98 | .15 | .09 | .19 | .44 | .38 | .24 | .12 | .23 | .26 | .38 | .23 | .39 | .18 |
| rs3790844 | chr1: 200007432 | NR5A 2 | .62 | .73 | .35 | .09 | .11 | .43 | .34 | .21 | .12 | .22 | .24 | .41 | .63 | .43 | .23 |
| rs3790843 | chr1: 200010824 | NR5A 2 | .58 | .96 | .22 | .13 | .21 | .65 | .54 | .26 | .17 | .27 | .29 | .61 | .70 | .65 | .32 |
| rs401681 | chr5: 1322087 | CLPT M1L-TERT | .42 | .99 | .94 | .95 | .98 | 1.0 | .94 | .92 | .83 | .97 | .92 | .64 | .88 | .63 | 1.0 |
All p-values were adjusted for age and gender.
chromosome number and position (human reference genome hg19).
Gene by age-specific BMI interaction by Model (1).
Adjusted minimum p-value (minP) for age-specific interactions based on the Bonferroni procedure.
minP based on parametric bootstrap.
aveBM: average BMI; maxBMI: maximum BMI; aucBMI: area under the BMI curve.
PC1: the first PC from multivariate PCA; PC95: leading PCs explaining at least 95% of total variation.
Score test p-value for gene by longitudinal BMI interaction via multiple logistic regression Model (2).
Functional logistic regression (FLR)-based score test and Sum of Squared score (SSU) test.
To evaluate possible confounding effect of cancer-related weight loss in patients, we performed a sensitivity analysis and set the BMI information in the age interval 50–59 years to missing should a patient be diagnosed during their 50s (n = 167 cases). Since the PACE-FPCA framework allows missing values, we were able to fit the FLR interaction Model (9) as previously described for complete BMI information. The rs8050136 by longitudinal BMI interaction remained nominally significant by the FLR-based SSU test with a p-value = 0.016, suggesting that our analyses based on complete BMI were unlikely to be confounded by the reverse causality derived from pancreatic cancer-associated weight loss.
Also shown in Table 1, two ad hoc summaries of the longitudinal BMI, including “aveBMI”, “aucBMI”, were able to detect the rs8050136 by BMI interaction (both p-values = 0.03), while “maxBMI” did not identify it (p-value = 0.09). As the time points were equally spaced and each individual had the same number of measurements in this data example, it is not difficult to see that “aveBMI” was approximately a re-scaled version of “aucBMI”, which explained why they gave similar results across the SNPs. A closer look revealed that “aveBMI” and “aucBMI” were highly correlated with BMI in the 30’s, while “maxBMI” had the highest correlation with BMI in the 50’s, consistent with the age-specific BMI interaction analysis results. The first PC from multivariate PCA, explaining 91% of the total variation, had roughly the same loadings across the five BMI measures, and thus, was highly correlated with “aveBMI”. Not surprisingly it was able to identify the rs8050136 by BMI interaction (p-value = 0.03), while the first three PCs, explaining 96% of the total variation, had an insignificant score test p-value = 0.11 due to the extra degrees of freedom. Although the multivariate PCA and the FPCA performed similarly in detecting the rs8050136 by BMI interaction, we’d like to emphasize that the FPCA is more flexible and powerful in that it can accommodate missing values, both regularly and irregularly measured longitudinal exposures, as well as measurement errors. More importantly, the FPCA coupled with the FLR can not only test for interaction effects, but also estimate the time-varying interaction effects as exemplified by Figure 3.
We also identified significant gender by longitudinal BMI interaction using the proposed FLR model with an SSU test p-value = 0.037 (Table S3 and S4). Further analysis of the gender-specific time-varying coefficient for the longitudinal BMI revealed that the interaction was the strongest in the age interval 40–49 years (Figure S6), in contrast to age intervals 20–29 and 30–39 years for SNP rs8050136 in the FTO gene. Our analyses here exemplify the need to look at the entire range of longitudinal exposure in the GxE analysis [Hutter et al., 2013] and the proposed FLR model coupled with the FPCA thereby provides a powerful tool for such investigations.
Simulation studies
Simulation I: Type I error and power
To further evaluate the proposed method’s properties, we performed a simulation study that resembled the pancreatic cancer real data example. We used the parameter values estimated from the real data when generating the simulated genotype, longitudinal BMI and disease status. Specifically, following [Leng and Muller, 2006], the disease status of each subject was simulated based on the following model: , where Gi was simulated from Binomial (2, p = 0.4) to resemble the FTO SNP rs8050136 with a minor allele frequency (MAF) of 40%, and the three FPC scores were independently simulated from normal distributions FPCi1~N(0, 7.12), FPCi2~N(0, 2.32), and FPCi3~N(0, 0.762). We set β0 to be −4.6, corresponding to a baseline 1% disease prevalence, and other parameters estimated from the pancreatic cancer dataset: (βG, β1, β2, β3, βG1, βG2, βG3)′ = (0.04,0.048, −0.068,0.25,0,0,0)′ and (0.04,0.02, −0.02,0.28,0.03, −0.03,0.02)′ to evaluate the Type I error and power, respectively. The latter parameter values were based on the rs8050136 by longitudinal BMI interaction analysis unadjusted for age and gender (Table S5). We generated the observed BMI profiles at 5 equally-spaced time points which corresponded to the 5 age intervals, according to the following model without measurement error, , or the classical measurement error model , where εij~N(0, σ̂2) or εij~N(0, (2σ̂)2), σ̂ = 1.2 was the standard deviation for the measurement error estimated from the real data, and μ̂(t) and ρ̂k(t) were the estimated mean function and PFCs. For each simulation replicate, we generated a large homogeneous study population and then randomly sampled 1,000 cases and 1,000 controls to form a simulated dataset. We applied the proposed FLR coupled with PACE-based FPCA (Model (9)) and age-specific BMI interaction analysis methods (Models (1) and (2)) to the simulated datasets and evaluated the empirical Type I error and power under significance level α=0.05 based on 2,000 replications. To further evaluate the Type I error at a lower α level, for example, 0.001, we also increased the replications to 20,000.
Results from Simulation I
As shown in Table 2, all methods under consideration maintained the Type I error at the nominal level except the unadjusted minimum p-value (minP) of the age-specific BMI interaction analysis, which had substantial Type I error inflation. On the other hand, the Bonferroni adjusted minP appeared to have conservative Type I errors, while the parametric-bootstrap adjusted minP was less conservative. Increased variances of the measurement error did not affect the Type I error control except for the unadjusted minP. The same conclusions held under lower α levels (0.01, 0.001 and 0.0005) based on 20,000 replications (Table S6).
Table 2.
Empirical Type I error at significance level
| Measurement error in FPCA simulation modela |
BMIc (14– 19 yrs.) |
BMI (20– 29 yrs.) |
BMI (30– 39 yrs.) |
BMI (40– 49 yrs.) |
BMI (50– 59 yrs.) |
BMI MinPd (unadjusted) |
BMI MinPe (Bonf.) |
BMI MinPf (Parametric bootstrap) |
BMIg (Score) |
FLRh (LRT) |
FLRh (Score) |
FLRh (SSU) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| w/o error | .051b | .049 | .048 | .047 | .054 | .103 | .020 | .025 | .049 | .052 | .052 | .048 |
| with error (σ) | .047 | .049 | .047 | .047 | .049 | .121 | .026 | .031 | .044 | .050 | .050 | .050 |
| with error (2σ) | .041 | .047 | .046 | .049 | .047 | .140 | .031 | .038 | .043 | .052 | .051 | .044 |
Whether observed BMI was contaminated by measurement error in the simulation model; σ is the estimated standard deviation of measurement error from the real data.
All empirical Type I errors were based on 2,000 simulation replications with 1,000 cases and 1,000 controls in each replicate.
Gene by age-specific BMI interaction by Model (1).
Unadjusted minimum p-value (minP) for age-specific interactions.
Adjusted minP for age-specific interactions based on the Bonferroni procedure.
Adjusted minP for age-specific interactions based on parametric bootstrap.
Score test for gene by longitudinal BMI interaction via multiple logistic regression Model (2).
Functional logistic regression (FLR)-based likelihood ratio test (LRT), score test and Sum of Squared score (SSU) test.
Table 3 shows the empirical statistical powers at α=0.05. The FLR-based SSU test was the most powerful across different simulation scenarios. Although age-specific BMI interaction analysis in certain age intervals might be more powerful than the FLR-based SSU, the minP tests (Bonferroni-adjusted and parametric bootstrap-adjusted to take into account multiple testing) were always dominated by the SSU test. Noticeably, even though the unadjusted minP appeared to have the highest power, it could not control the Type I error (Table 2) and should be excluded from the comparison. As the variance of the measurement error increased, most tests’ performance deteriorated; however, the FLR-based SSU test was quite robust to increased measurement error. The FLR-based LRT and score tests had comparable statistical power as expected. Although they were less powerful than the score test in the multiple BMI-based logistic regression Model (2) when there was no measurement error in the observed BMI, their power loss was less severe than the latter in the presence of increased measurement errors, suggesting that the proposed FLR model was more robust to contaminated longitudinal exposure measurements. Nevertheless, the FLR-based LRT and score tests were less powerful than the SSU test, which we recommend to use coupled with the proposed FLR model.
Table 3.
Empirical statistical power at significance level
| Measurement error in FPCA simulation modela |
BMIc (14– 19 yrs.) |
BMI (20– 29 yrs.) |
BMI (30– 39 yrs.) |
BMI (40– 49 yrs.) |
BMI (50– 59 yrs.) |
BMI MinPc (unadjusted) |
BMI MinPe (Bonf.) |
BMI MinPf (Parametric bootstrap) |
BMIg (Score) |
FLRh (LRT) |
FLRh (Score) |
FLRh (SSU) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| w/o error | .768b | .842 | .837 | .762 | .579 | .873i | .740 | .754 | .794 | .705 | .708 | .811 |
| with error (σ) | .727 | .815 | .816 | .734 | .570 | .893i | .724 | .736 | .593 | .690 | .690 | .810 |
| with error (2σ) | .633 | .739 | .754 | .658 | .509 | .894i | .711 | .719 | .564 | .650 | .655 | .792 |
Whether observed BMI was contaminated by measurement error in the simulation model; σ is estimated standard deviation of measurement error from the real data.
All empirical powers were based on 2,000 simulation replications with 1,000 cases and 1,000 controls in each replicate.
Gene by age-specific BMI interaction by Model (1).
Unadjusted minimum p-value (minP) for age-specific interactions.
Adjusted minP for age-specific interactions based on the Bonferroni procedure.
Adjusted minP for age-specific interactions based on parametric bootstrap.
Score test for gene by longitudinal BMI interaction via multiple logistic regression Model (2).
Functional logistic regression (FLR)-based likelihood ratio test (LRT), score test and Sum of Squared score (SSU) test.
Type I error cannot be controlled as shown in Table 2.
Simulation II: effect of the number of longitudinal measurements
We conducted additional simulations to evaluate the effect of the number of longitudinal measurements on the Type I error and power of the proposed FLR method. Specifically, we followed the setup in Simulation I, but, instead of 5 time points, we generated the observed BMI at 3, 4, 5, 7, 10 and 20 equally spaced time points between the two endpoints, 1 and 5, and always included these two points. For example, when there were 3 measurements, each individual’s BMI was observed at time points 1, 3 and 5 with measurement error standard deviation σ̂ = 1.2. We used the modified BIC method (the default in PACE) to select the optimal number of FPCs. The empirical Type I error rate and power were based on 1,000 and 200 replications, respectively. As shown in Table S7, both FLR-SSU and multiple logistic regression fitting of the observed BMI (Model (2)) were able to control the Type I error rate at the nominal level regardless of the number of longitudinal measurements. There was a 3% increase in power when the number of measurements increased from 3 to 4 for the proposed FLR-SSU test, while the power remained almost constant with further increased numbers of measurements beyond 4. On the other hand, the multiple logistic regression’s power severely deteriorated as the number of measurements increased beyond 4, because of the multicollinearity among the multiple longitudinal measurements. This simulation study supported that we were able to reliably test for interaction effects with 5 BMI measurements in the pancreatic cancer dataset using the FLR-SSU test.
Simulation III: model robustness
We also performed simulations to evaluate how robust the proposed FLR method was with respect to different model misspecifications, including (a) incorrect number of FPCs, (b) misspecified exposure main effects, and (c) longitudinal BMI not simulated from the FPCA model.
First, we evaluated the Type I error and power when the disease status was dependent on three FPCs under Simulation I, but only the first one or two were selected in the FPCA step. This incorrect number of FPCs was possible due to noise in the data and model selection uncertainty in the first FPCA step. As shown in Table S8, the FLR model coupled with the Wald test (for one FPC) or the SSU test (for two or three FPCs) was able to control the Type I error rate at the nominal level even with incorrect number of FPCs, i.e., one or two FPCs; in addition, the power was around 81% regardless of the number of FPCs included, likely because the first FPC had the largest interaction effect size among the three under Simulation I resembling the real data (Table S5).
Second, we evaluated the effect of misspecified exposure main effects on the Type I error and power. It has been reported in the literature that model misspecifications, especially the exposure main effects, can lead to inflated Type I error in GxE tests [Cornelis et al., 2012; Tchetgen Tchetgen and Kraft, 2011]. We first tested whether a quadratic term of age-specific BMI main effect was needed in Model (1) in the pancreatic cancer dataset, and found no significant quadratic term for any of the five age intervals. We also fitted a generalized spline regression to age-specific BMI. As shown in Figure S7, BMI in the 30–39 years age interval (denoted by BMI30) appeared to be linearly associated with the logit of disease risk. Therefore, a linear term of age-specific BMI main effect turned out to be adequate in the real data application. We further carried out simulations to evaluate the robustness of Models (1) and (2) and the proposed FLR model. We simulated longitudinal BMI from the FPCA model as in Simulation I, but the disease status was only dependent on BMI30: . The simulation details and results are described in Supplemental Text Section 3.1. In summary, we confirmed the previous finding reported in the literature that misspecified main effect of BMI30 led to inflated Type I error rate; in addition, we found that, for age-specific BMI other than BMI30, even the interaction Model (1) with quadratic term of BMI main effect had inflated Type I error. In contrast, the proposed FLR model controlled the Type I error satisfactorily and remained high power without explicitly incorporating quadratic main or interaction effects. Although the FLR model appeared to be robust to nonlinear interaction effects, we’d like to point out that the FLR model was developed to estimate and test for time-varying main and interaction effects, i.e., for datasets with longitudinal exposure within the same individual, rather than for modeling nonlinear effects of a static exposure, e.g., BMI30, across individuals. Nevertheless, because multiple FPCs were included in the FLR model, some nonlinear effects of the exposure at a given time point might be captured, leading to the appealing model robustness.
Finally, we simulated the longitudinal BMI and disease status from non-FPCA/FLR model to further evaluate the model robustness. As detailed in Supplemental Text Section 3.2, we resampled the observed rs8050136 genotype and longitudinal BMI pairs with replacement from the pooled cases and controls in the pancreatic cancer dataset, and generated the disease status based on the real data-fitted multiple logistic regression Model (2). As shown in Table S10, the comparative performance of the different tests was qualitatively the same as that in Simulation I, and the FLR-SSU test remained the most powerful one.
Discussion
We have proposed a novel FLR-based statistical framework for detecting gene by longitudinal environmental exposure interactions. The proposed two-stage approach first summarizes the longitudinal exposure into a few FPCs via the PACE method which takes into account possible measurement errors, and then tests for interaction between a SNP and FPCs in a FLR model. Using data from a case-control study of pancreatic cancer and real data-based simulations, we demonstrated that the SSU test nested in the FLR model was more powerful than alternative methods. In addition, the SSU test was found to be robust to measurement errors in the longitudinal environmental exposure. Although in our real data example the environmental exposure was measured on a regular time grid, the proposed method can be equally applied to irregularly measured time-varying exposures as commonly seen in observational studies. Since the first-stage PACE-based FPCA only needs to be applied once for all SNPs, the proposed method can be easily scaled up to genome-wide scale interaction scan. Therefore, we recommend the use of the FLR model coupled with the SSU test to detect gene by longitudinal exposure interactions.
It has been well recognized that early-life exposures, e.g., maternal, childhood or adolescence exposures, may be critical to disease occurrence later in life [Hutter et al., 2013; Sutcliffe and Colditz, 2013]. Therefore, it is important to consider long-term exposure history beyond the immediate short window prior to disease onset to identify the critical window of disease development. Powerful statistical methods have also recently been proposed to detect time-varying gene by cumulative environmental exposure interactions for repeated-measured quantitative phenotypes, i.e., G x E x time interactions [Ko et al., 2013; Mukherjee et al., 2012b]. To the best of our knowledge, the proposed FLR method described here is the first to detect gene by longitudinal environmental exposure interactions in a case-control study. It would be of interest to extend the current framework to quantitative and longitudinal phenotypes, for example, via the functional linear model for functional response variable [Müller, 2009].
Recently it has been demonstrated that robustly identified GxE interactions can improve disease risk prediction and help develop intervention strategies [Garcia-Closas et al., 2013]. It remains a great challenge to develop effective prevention and intervention strategies for pancreatic cancer in the general population due to its low incidence rate and a poor understanding of the disease etiology. However, the identified FTO by early adulthood obesity interaction, once replicated in independent studies, may hold the promise to be incorporated into and improve the existing risk prediction model for pancreatic cancer [Klein et al., 2013]. The risk model could then be used to identify high-risk individuals, for example, those who are smokers and have family history of pancreatic cancer, minor allele homozygote of rs8050136 and obesity in early adulthood, for targeted interventions, such as participation in weight loss and smoking cessation programs.
To summarize the longitudinal exposure, we employed the FPCA which is conceptually similar to the multivariate PCA. Both methods are used for dimension reduction and have been applied in genetic studies. For example, the PCA has been used to control population stratification and to summarize multiple SNPs in a region in SNP-set association tests [Wei et al., 2012], while the FPCA has been employed in rare variant association tests to model rare mutation profiles [Luo et al., 2011]. The PCA and FPCA, however, differ in the many aspects. First, the FPCA models functional data with a time or spatial domain, and, thus, measurements at different time points, unlike in PCA, are not exchangeable. Second, the FPCA is often coupled with some smoothing procedures to take into account measurement errors by borrowing information from neighboring measurements, e.g., either smoothing the mean and covariance functions as in the PACE method, or smoothing the raw longitudinal trajectories as advocated by others [Ramsay and Silverman, 2005]. Third, the FPCA can be applied to longitudinal data measured at either regular or irregular time points and can accommodate missing data, while the PCA can only be applied to regularly measured data without missing values.
In the FPCA-FLR framework, we propose to perform the FPCA on the combined case-control samples rather than only control samples for two main reasons. First, ignoring disease status in the FPCA step avoids differential estimation errors between cases and controls as well as using the disease status twice, and thus ensures that the Type I error rate is maintained at the nominal level in the subsequent FLR association test step. This is in line with the “EG2” two-step GxE test of [Murcray et al., 2009] and multivariate PCA-based SNP-set association test of case-control data [Wei et al., 2012]. Second, it is necessary to perform the FPCA on the pooled samples in order to extract longitudinal exposure patterns, i.e., the FPCs, which may be only present in the cases, but nevertheless are relevant with the disease association and interaction with the genetic factor. Another related concern is that, given the FPCA-FLR method was only applied to cohort data before [Müller, 2005; Yao et al., 2005], whether we can apply it to outcome-dependent sampling schemes, such as the case-control study design. Intuitively, if we consider the FPCA as a means of applying dimension reduction to the covariates prior to association testing, it should not matter whether we have cohort or case-control data. As for effect size estimation, it has been well known that valid estimation of the odds ratio and its asymptotic variance can be obtained by applying the logistic regression model to case-control data as if the sampling were perspective [Prentice and Pyke, 1979]. Considering this result is established for simple exposure variables and the FPC scores in the FLR are nonlinear transformations of the original longitudinal exposures, we resorted to simulations to address the above concern. As detailed in Supplemental Text Section 3.3, we simulated cohort samples with disease prevalence around 50%, each consisting of roughly 1,000 cases and 1,000 controls, as well as case-control studies of 1,000 case-control pairs with baseline disease prevalence at 1%. We found that, between the cohort and case-control designs, the FLR model gave very similar estimates of the regression coefficients in terms of bias and variance (Table S11), supporting the validity of applying the FLR model to case-control data.
There are some potential limitations in our proposed statistical framework. First, the proposed method is two-stage: the first-stage FPCA is only applied to the pooled longitudinal exposures without considering the disease status and genetic data. While this approach has the advantages of maintaining the Type I error rate in the second-stage interaction test, generating data-adaptive and interpretable basis functions, i.e., the FPCs, and facilitating genome-wide interaction analysis, it is possible that the extracted FPCs contain irrelevant information about the disease status or GxE interactions, leading to reduced statistical power. It would be of interest to develop computational efficient one-step methods for detecting gene by longitudinal exposure interactions. Second, the longitudinal exposure data in our real data example is recalled BMI information collected by personal interviews, which, however, may be contaminated by recall bias and other measurement errors. Although our proposed method can accommodate the classical measurement errors [Carroll et al., 2006] and previous studies have found a high level of accuracy of self-reported past body weights compared with measured weights [Casey et al., 1991; Stevens et al., 1990], there is a lack of validation data for this study population and possible recall bias inherently associated with the case-control design cannot be excluded. On the other hand, in nested case-control studies within prospective longitudinal cohorts, such as the Framingham Heart Study [Splansky et al., 2007] and the Kaiser Permanente cohort of nearly 100,000 individuals with both GWAS and longitudinal electronic health records (EHR) [Hoffmann et al., 2011], exposure variables are more accurately measured and unlikely prone to recall bias. A recent study was able to investigate the association between childhood heights from age 8 to 13 years and adult prostate cancer risk in over 125,000 individuals by linking the Copenhagen School Health Records Register prospective cohort and the Danish Cancer Register [Cook et al., 2013]. Finally, as the research community increasingly appreciates the importance of exposure history across one’s lifespan on the risk of complex disease and its interaction with genetic factors [Hutter et al., 2013; Sutcliffe and Colditz, 2013], more and more studies, such as the National Children’s Study, are collecting accurately measured time-varying exposure information, thereby providing unprecedented opportunities for investigation into the complex interplay between genes and longitudinal environmental exposures.
R programs implementing the proposed FLR method will be posted on our website at: https://sites.google.com/site/utpengwei/
Supplementary Material
Acknowledgments
This research was supported by NIH grants R01CA169122, R01HL116720, R01HL106034 (to P.W.), a supplemental grant to R01CA98380 and the Sheikh Ahmed Center for Pancreatic Cancer Research Funds (to D.L.). We thank Dr. Wei Pan for helpful discussions and Ms. Sara Barton for editorial assistance. We are grateful to two anonymous reviewers for their many helpful and constructive comments that improved the presentation of the paper.
Footnotes
The authors declare no conflict of interest.
References
- American Cancer Society. Cancer Facts & Figures 2013. Atlanta: American Cancer Society;; 2013. [Google Scholar]
- Amundadottir L, Kraft P, Stolzenberg-Solomon RZ, Fuchs CS, Petersen GM, Arslan AA, Bueno-de-Mesquita HB, Gross M, Helzlsouer K, Jacobs EJ, et al. Genome-wide association study identifies variants in the ABO locus associated with susceptibility to pancreatic cancer. Nature Genetics. 2009;41(9):986–90. doi: 10.1038/ng.429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aschard H, Lutz S, Maus B, Duell EJ, Fingerlin TE, Chatterjee N, Kraft P, Van Steen K. Challenges and opportunities in genome-wide environmental interaction (GWEI) studies. Human Genetics. 2012;131(10):1591–613. doi: 10.1007/s00439-012-1192-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berndt SI, Gustafsson S, Magi R, Ganna A, Wheeler E, Feitosa MF, Justice AE, Monda KL, Croteau-Chonka DC, Day FR, et al. Genome-wide meta-analysis identifies 11 new loci for anthropometric traits and provides insights into genetic architecture. Nature Genetics. 2013;45(5):501–12. doi: 10.1038/ng.2606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhadra D, Daniels MJ, Kim S, Ghosh M, Mukherjee B. A Bayesian semiparametric approach for incorporating longitudinal information on exposure history for inference in case-control studies. Biometrics. 2012;68(2):361–70. doi: 10.1111/j.1541-0420.2011.01686.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bookman EB, McAllister K, Gillanders E, Wanke K, Balshaw D, Rutter J, Reedy J, Shaughnessy D, Agurs-Collins T, Paltoo D, et al. Gene-environment interplay in common complex diseases: forging an integrative model-recommendations from an NIH workshop. Genet Epidemiol. 2011;35(4):217–225. doi: 10.1002/gepi.20571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzkova P, Lumley T, Rice K. Permutation and parametric bootstrap tests for gene-gene and gene-environment interactions. Annals of Human Genetics. 2011;75(1):36–45. doi: 10.1111/j.1469-1809.2010.00572.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll RJ, Ruppert D, Stefanski LA, Crainiceanu C. Measurement Error in Nonlinear Models: A Modern Perspective. New York: Chapman & Hall; 2006. [Google Scholar]
- Casey VA, Dwyer JT, Berkey CS, Coleman KA, Gardner J, Valadian I. Long-term memory of body weight and past weight satisfaction: a longitudinal follow-up study. The American Journal of Clinical Nutrition. 1991;53(6):1493–8. doi: 10.1093/ajcn/53.6.1493. [DOI] [PubMed] [Google Scholar]
- Cook MB, Gamborg M, Aarestrup J, Sorensen TI, Baker JL. Childhood height and birth weight in relation to future prostate cancer risk: a cohort study based on the copenhagen school health records register. Cancer Epidemiology, Biomarkers & Prevention. 2013;22(12):2232–40. doi: 10.1158/1055-9965.EPI-13-0712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornelis MC, Tchetgen EJ, Liang L, Qi L, Chatterjee N, Hu FB, Kraft P. Gene-environment interactions in genome-wide association studies: a comparative study of tests applied to empirical studies of type 2 diabetes. American Journal of Epidemiology. 2012;175(3):191–202. doi: 10.1093/aje/kwr368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitzmaurice GM, Laird NM, Ware JH. Applied longitudinal analysis. Hoboken, N.J: Wiley; 2011. [Google Scholar]
- Garcia-Closas M, Rothman N, Figueroa JD, Prokunina-Olsson L, Han SS, Baris D, Jacobs EJ, Malats N, De Vivo I, Albanes D, et al. Common genetic polymorphisms modify the effect of smoking on absolute risk of bladder cancer. Cancer Research. 2013;73(7):2211–20. doi: 10.1158/0008-5472.CAN-12-2388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gauderman WJ, Zhang P, Morrison JL, Lewinger JP. Finding novel genes by testing G x E interactions in a genome-wide association study. Genet Epidemiol. 2013;37(6):603–13. doi: 10.1002/gepi.21748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goeman JJ, van de Geer S, van Houwelingen HC. Testing against a high dimensional alternative. J R Stat Soc B. 2006;68:477–493. [Google Scholar]
- Hindorff LA, Sethupathy P, Junkins HA, Ramos EM, Mehta JP, Collins FS, Manolio TA. Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proceedings of the National Academy of Sciences of the United States of America. 2009;106(23):9362–7. doi: 10.1073/pnas.0903103106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann TJ, Kvale MN, Hesselson SE, Zhan Y, Aquino C, Cao Y, Cawley S, Chung E, Connell S, Eshragh J, et al. Next generation genome-wide association tool: design and coverage of a high-throughput European-optimized SNP array. Genomics. 2011;98(2):79–89. doi: 10.1016/j.ygeno.2011.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu L, Jiao S, Dai JY, Hutter C, Peters U, Kooperberg C. Powerful cocktail methods for detecting genome-wide gene-environment interaction. Genet Epidemiol. 2012;36(3):183–94. doi: 10.1002/gepi.21610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutter CM, Mechanic LE, Chatterjee N, Kraft P, Gillanders EM. Gene-Environment Interactions in Cancer Epidemiology: A National Cancer Institute Think Tank Report. Genet Epidemiol. 2013;37(7):643–657. doi: 10.1002/gepi.21756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiao S, Hsu L, Bezieau S, Brenner H, Chan AT, Chang-Claude J, Le Marchand L, Lemire M, Newcomb PA, Slattery ML, et al. SBERIA: set-based gene-environment interaction test for rare and common variants in complex diseases. Genet Epidemiol. 2013;37(5):452–64. doi: 10.1002/gepi.21735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein AP, Lindstrom S, Mendelsohn JB, Steplowski E, Arslan AA, Bueno-de-Mesquita HB, Fuchs CS, Gallinger S, Gross M, Helzlsouer K, et al. An absolute risk model to identify individuals at elevated risk for pancreatic cancer in the general population. PLoS ONE. 2013;8(9):e72311. doi: 10.1371/journal.pone.0072311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ko YA, Saha-Chaudhuri P, Park SK, Vokonas PS, Mukherjee B. Novel likelihood ratio tests for screening gene-gene and gene-environment interactions with unbalanced repeated-measures data. Genet Epidemiol. 2013;37(6):581–91. doi: 10.1002/gepi.21744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kooperberg C, Leblanc M. Increasing the power of identifying gene x gene interactions in genome-wide association studies. Genet Epidemiol. 2008;32(3):255–63. doi: 10.1002/gepi.20300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leng X, Muller HG. Classification using functional data analysis for temporal gene expression data. Bioinformatics. 2006;22(1):68–76. doi: 10.1093/bioinformatics/bti742. [DOI] [PubMed] [Google Scholar]
- Li D, Morris JS, Liu J, Hassan MM, Day RS, Bondy ML, Abbruzzese JL. Body mass index and risk, age of onset, and survival in patients with pancreatic cancer. JAMA. 2009;301(24):2553–62. doi: 10.1001/jama.2009.886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li S, Mukherjee B, Taylor JM, Rice KM, Wen X, Rice JD, Stringham HM, Boehnke M. The Role of Environmental Heterogeneity in Meta-Analysis of Gene-Environment Interactions With Quantitative Traits. Genet Epidemiol. 2014 doi: 10.1002/gepi.21810. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Wang N, Carroll RJ. Generalized functional linear models with semiparametric single-Index interactions. J Am Stat Assoc. 2010;105(490):621–633. doi: 10.1198/jasa.2010.tm09313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo L, Boerwinkle E, Xiong M. Association studies for next-generation sequencing. Genome Research. 2011;21(7):1099–108. doi: 10.1101/gr.115998.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio TA. Bringing genome-wide association findings into clinical use. Nature Reviews Genetics. 2013;14(8):549–58. doi: 10.1038/nrg3523. [DOI] [PubMed] [Google Scholar]
- Mechanic LE, Chen HS, Amos CI, Chatterjee N, Cox NJ, Divi RL, Fan R, Harris EL, Jacobs K, Kraft P, et al. Next generation analytic tools for large scale genetic epidemiology studies of complex diseases. Genet Epidemiol. 2012;36:22–35. doi: 10.1002/gepi.20652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukherjee B, Ahn J, Gruber SB, Chatterjee N. Testing gene-environment interaction in large-scale case-control association studies: possible choices and comparisons. Am J Epidemiol. 2012a;175(3):177–90. doi: 10.1093/aje/kwr367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukherjee B, Chatterjee N. Exploiting gene-environment independence for analysis of case-control studies: an empirical Bayes-type shrinkage estimator to trade-off between bias and efficiency. Biometrics. 2008;64(3):685–94. doi: 10.1111/j.1541-0420.2007.00953.x. [DOI] [PubMed] [Google Scholar]
- Mukherjee B, Ko YA, Vanderweele T, Roy A, Park SK, Chen J. Principal interactions analysis for repeated measures data: application to gene-gene and gene-environment interactions. Statistics in Medicine. 2012b;31(22):2531–51. doi: 10.1002/sim.5315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller H-G. Functional modeling of longitudinal data. In: Fitzmaurice G, Davidian M, Verbeke G, Molenberghs G, editors. Longitudinal Data Analysis (Handbooks of Modern Statistical Methods) New York: Wiley; 2009. pp. 223–252. [Google Scholar]
- Müller H-G, Stadtmüller U. Generalized functional linear models. Ann Statist. 2005;33(2):774–805. [Google Scholar]
- Murcray CE, Lewinger JP, Conti DV, Thomas DC, Gauderman WJ. Sample size requirements to detect gene-environment interactions in genome-wide association studies. Genet Epidemiol. 2011;35(3):201–10. doi: 10.1002/gepi.20569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murcray CE, Lewinger JP, Gauderman WJ. Gene-environment interaction in genome-wide association studies. Am J Epidemiol. 2009;169(2):219–26. doi: 10.1093/aje/kwn353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W. Asymptotic tests of association with multiple SNPs in linkage disequilibrium. Genet Epidemiol. 2009;33(6):497–507. doi: 10.1002/gepi.20402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W. Relationship between genomic distance-based regression and kernel machine regression for multi-marker association testing. Genet Epidemiol. 2011;35:211–216. doi: 10.1002/gepi.20567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W, Basu S, Shen X. Adaptive tests for detecting gene-gene and gene-environment interactions. Hum Hered. 2011;72(2):98–109. doi: 10.1159/000330632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepe MS, Heagerty P, Whitaker R. Prediction using partly conditional time-varying coefficients regression models. Biometrics. 1999;55(3):944–950. doi: 10.1111/j.0006-341x.1999.00944.x. [DOI] [PubMed] [Google Scholar]
- Petersen GM, Amundadottir L, Fuchs CS, Kraft P, Stolzenberg-Solomon RZ, Jacobs KB, Arslan AA, Bueno-de-Mesquita HB, Gallinger S, Gross M, et al. A genome-wide association study identifies pancreatic cancer susceptibility loci on chromosomes 13q22.1, 1q32.1 and 5p15.33. Nature Genetics. 2010;42(3):224–8. doi: 10.1038/ng.522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prentice RL, Pyke R. Logistic Disease Incidence Models and Case-Control Studies. Biometrika. 1979;66(3):403–411. [Google Scholar]
- Ramsay JO, Silverman BW. Functional data analysis. New York: Springer-Verlag; 2005. [Google Scholar]
- Sanchez BN, Hu H, Litman HJ, Tellez-Rojo MM. Statistical methods to study timing of vulnerability with sparsely sampled data on environmental toxicants. Environmental Health Perspectives. 2011;119(3):409–15. doi: 10.1289/ehp.1002453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorensen H, Goldsmith J, Sangalli LM. An introduction with medical applications to functional data analysis. Statistics in Medicine. 2013;32(30):5222–40. doi: 10.1002/sim.5989. [DOI] [PubMed] [Google Scholar]
- Splansky GL, Corey D, Yang Q, Atwood LD, Cupples LA, Benjamin EJ, D’Agostino RB, Sr, Fox CS, Larson MG, Murabito JM, et al. The Third Generation Cohort of the National Heart, Lung, and Blood Institute’s Framingham Heart Study: design, recruitment, and initial examination. Am J Epidemiol. 2007;165(11):1328–35. doi: 10.1093/aje/kwm021. [DOI] [PubMed] [Google Scholar]
- Stevens J, Keil JE, Waid LR, Gazes PC. Accuracy of current, 4-year, and 28-year self-reported body weight in an elderly population. Am J Epidemiol. 1990;132(6):1156–63. doi: 10.1093/oxfordjournals.aje.a115758. [DOI] [PubMed] [Google Scholar]
- Sutcliffe S, Colditz GA. Prostate cancer: is it time to expand the research focus to early-life exposures? Nature Reviews Cancer. 2013;13(3):208–518. doi: 10.1038/nrc3434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang H, Dong X, Hassan M, Abbruzzese JL, Li D. Body mass index and obesity- and diabetes-associated genotypes and risk for pancreatic cancer. Cancer Epidemiology, Biomarkers & Prevention. 2011;20(5):779–92. doi: 10.1158/1055-9965.EPI-10-0845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang H, Wei P, Duell EJ, Risch HA, Olson SH, Bueno-de-Mesquita HB, Gallinger S, Holly EA, Petersen GM, Bracci PM, et al. Axonal guidance signaling pathway interacting with smoking in modifying the risk of pancreatic cancer: A gene and pathway-based interaction analysis of GWAS data. Carcinogenesis. 2014a;35:1039–1045. doi: 10.1093/carcin/bgu010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang H, Wei P, Duell EJ, Risch HA, Olson SH, Bueno-de-Mesquita HB, Gallinger S, Holly EA, Petersen GM, Bracci PM, et al. Genes-environment interactions in obesity- and diabetes-associated pancreatic cancer: a GWAS data analysis. Cancer Epidemiology, Biomarkers & Prevention. 2014b;23(1):98–106. doi: 10.1158/1055-9965.EPI-13-0437-T. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen EJ, Kraft P. On the robustness of tests of genetic associations incorporating gene-environment interaction when the environmental exposure is misspecified. Epidemiology. 2011;22(2):257–61. doi: 10.1097/EDE.0b013e31820877c5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas D. Gene--environment-wide association studies: emerging approaches. Nature reviews Genetics. 2010;11(4):259–72. doi: 10.1038/nrg2764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher PM, Brown MA, McCarthy MI, Yang J. Five years of GWAS discovery. Am J Hum Genet. 2012;90(1):7–24. doi: 10.1016/j.ajhg.2011.11.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei P, Tang H, Li D. Insights into pancreatic cancer etiology from pathway analysis of genome-wide association study data. PLoS ONE. 2012;7(10):e46887. doi: 10.1371/journal.pone.0046887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu C, Kraft P, Zhai K, Chang J, Wang Z, Li Y, Hu Z, He Z, Jia W, Abnet CC, et al. Genome-wide association analyses of esophageal squamous cell carcinoma in Chinese identify multiple susceptibility loci and gene-environment interactions. Nature Genetics. 2012;44(10):1090–7. doi: 10.1038/ng.2411. [DOI] [PubMed] [Google Scholar]
- Wu MC, Kraft P, Epstein MP, Taylor DM, Chanock SJ, Hunter DJ, Lin X. Powerful SNP-set analysis for case-control genome-wide association studies. Am J Hum Genet. 2010;86(6):929–42. doi: 10.1016/j.ajhg.2010.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao F, Müller HG, Wang JL. Functional data analysis for sparse longitudinal data. J Am Stat Assoc. 2005;100:577–590. [Google Scholar]
- Zuk O, Hechter E, Sunyaev SR, Lander ES. The mystery of missing heritability: Genetic interactions create phantom heritability. Proceedings of the National Academy of Sciences of the United States of America. 2012;109(4):1193–8. doi: 10.1073/pnas.1119675109. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.