Combining family- and population-based imputation data for association analysis of rare and common variants in large pedigrees

Abstract

In the last two decades, complex traits have become the main focus of genetic studies. The hypothesis that both rare and common variants are associated with complex traits is increasingly being discussed. Family-based association studies using relatively large pedigrees are suitable for both rare and common variant identification. Because of the high cost of sequencing technologies, imputation methods are important for increasing the amount of information at low cost. A recent family-based imputation method, GIGI, is able to handle large pedigrees and accurately impute rare variants, but does less well for common variants where population-based methods perform better. Here, we propose a flexible approach to combine imputation data from both family- and population-based methods. We also extend the association test SKAT-RC, originally proposed for data from unrelated subjects, to family data in order to make use of such imputed data. We call this extension “famSKAT-RC”. We compare the performance of famSKAT-RC and several other existing burden and kernel association tests. In simulated pedigree sequence data, our results show an increase of imputation accuracy from use of our combining approach. Also, they show an increase of power of the association tests with this approach over the use of either family- or population-based imputation methods alone, in the context of rare and common variants. Moreover, our results showed better performance of famSKAT-RC compared to the other considered tests, in most scenarios investigated here.

Introduction

In the last two decades, complex traits have become the main focus of genetic studies. Complex traits are likely to be influenced by variants in several genes located on different chromosomes [Bodmer and Bonilla 2008; Frazer, et al. 2009]. Many plausible hypotheses postulate the implication of multiple genetic factors in complex traits, including copy number variations (CNV), gene-gene and gene-environment interactions, and multiple rare variants [Bansal, et al. 2010b]. Linkage analysis in pedigrees has succeeded in identifying mutations in multiple genes for rare Mendelian forms of some complex traits [Delepine, et al. 1997; Goate, et al. 1991; Paunio, et al. 2001; Polymeropoulos, et al. 1997; Saad, et al. 2011; Schellenberg, et al. 1992; Zimprich, et al. 2004]. For some of these traits, Genome Wide Association Studies (GWAS) in data of unrelated subjects have also succeeded in identifying common variants in the same genes discovered by linkage analysis, such as the gene SNCA associated with Parkinson’s disease [Nalls, et al. 2011; Saad, et al. 2011]. This suggests that there is a continuum between the spectrum of rare and common variants associated with complex traits, which signifies the investigation of the “Multiple Rare and Common Variants - Complex Disease” (MRCV-CD) hypothesis. The MRCV-CD hypothesis states that rare and common variants are both jointly involved in at least some complex traits [Curtis 2012; Ionita-Laza, et al. 2013].

For common variant identification, the majority of GWAS are based on population-based designs that use unrelated subjects. For adequate sample sizes, GWAS are relatively powerful for identifying common variants [Risch and Merikangas 1996], which generally have moderate to small effects on complex traits. However for detecting rare variants, which are likely to have large effects and possibly obvious functional consequences [Cirulli and Goldstein 2010], GWAS with unrelated subjects lack power for available/feasible sample sizes. In this context, traditional family-based linkage analyses, which are fairly robust to allelic heterogeneity [Ott 1991], are well known to be more powerful. Nonetheless, the rare functional variant model is not inconsistent with the absence of secure linkage evidence for most common diseases [Cirulli and Goldstein 2010]. Therefore, family-based GWAS appear to be an attractive and well suited option for the study of rare variants. Their advantage is the enrichment of copies of rare alleles in pedigrees [Wijsman 2012]. Unlike linkage analysis, family-based GWAS are also powerful for identifying association with common variants. The reason this design has not yet been widely used is the difficult and expensive need to sample family members coupled with some limitations to available analytical tools [Bansal, et al. 2010b]. With the increasing discussions about the involvement of both rare and common variants [Curtis 2012; Gibson 2011; Ionita-Laza, et al. 2013; Iyengar and Elston 2007], separately or jointly in complex trait etiologies, and development of suitable analytical tools, family-based GWAS have become practical, and useful for the identification of new susceptibility genes. Several association tests have been proposed to deal with rare and common variants jointly, such as SKAT/famSKAT [Chen, et al. 2013; Schifano, et al. 2012; Schifano, et al. 2013; Wu, et al. 2011], SKAT-RC [Ionita-Laza, et al. 2013], and CMC (Combined Multivariate Collapsing, [Li and Leal 2008]). The last two tests split rare and common SNPs into two bins and treat them separately via a kernel test (SKAT-RC) and multiple regression (CMC) framework. The SKAT-RC and CMC tests have been proposed for population-based designs but not yet for family-based designs.

With the rapid advances of current sequencing technologies, rare and common variants can be genotyped at the same time. The genotyping quality depends on several factors including sequencing depth. The required sequencing depth for good genotyping quality of rare variants is greater than that required for common variants [Bansal, et al. 2010a]. Despite the decrease in sequencing costs, performing large GWAS on sequence data is still cost-prohibitive. In addition, some subjects cannot be sequenced because of the absence of DNA or its low quantity and quality (especially for diseases with late onset age [Jacobs, et al. 2012; Laurie, et al. 2012]). Interestingly, the pseudo-sequencing strategy based on imputation makes these studies more affordable. This strategy consists of combining sequence data on a small subset of subjects with SNP or other marker data on the remaining subjects to finally obtain imputed sequence data for the un-sequenced subjects. The idea of imputation came from family-based designs: in the same pedigree, subjects share large chunks of chromosomes, typically quantified by identity by descent estimates (IBD). So basically, if we know the chromosome marker allele data on a few subjects at a particular marker position and we know how these chromosomes are transmitted in the pedigree, we may impute the missing chromosome marker alleles on all pedigree subjects who inherited the same copy of the chromosome at the position of the marker. The same idea has been extended to population-based designs [Li, et al. 2009] under the assumption that all humans belong to one big family with a large number of generations. Therefore, the shared chunks of chromosomes between unrelated subjects are much smaller than the shared chunks between family subjects. These small chunks of chromosomes are typically quantified by linkage disequilibrium (LD) blocks. LD and IBD are orthogonal sources of correlation information used by population-based (MACH [Li, et al. 2006], IMPUTE [Marchini, et al. 2007], and BEAGLE [Browning and Browning 2009]) vs, family-based (MERLIN [Burdick, et al. 2006] and GIGI [Cheung, et al. 2013]) imputation methods, respectively.

Family-based imputation is especially challenging for large pedigrees. GIGI (Genotype Imputation Given Inheritance) is able to handle large pedigrees, accurately impute rare variants (Minor Allele Frequency (MAF) ≤ 0.01), and also impute data on completely untyped subjects. However, GIGI’s authors showed in a limited evaluation that for common variants, GIGI can be moderately outperformed by the population-based imputation method implemented by BEAGLE, which ignores pedigree structure. On the other hand, they showed that BEAGLE has much poorer imputation performance for rare variants. These conclusions were not investigated for different LD patterns or for a variety of pedigree structures. Yet, if the LD between common SNPs is low, the imputation accuracy of BEAGLE decreases [Browning and Browning 2009] and hence GIGI may provide better accuracy in such regions, even for common SNPs. In addition, for the spectrum of uncommon variants with MAF ranging between 0.01 and 0.1, the best imputation accuracy might come from either GIGI or BEAGLE. Therefore, a natural question is how to combine the orthogonal sources of correlation information used by GIGI (IBD) and BEAGLE (LD) in order to increase the imputation accuracy in family-based designs and then to efficiently perform association studies under the MRCV-CD hypothesis.

In Genetic Analysis Workshop 18, a first attempt to combine imputation data from GIGI and BEAGLE was made, providing promising results [Marchani, et al. (in press)]. In our study here, we extend this idea and propose a practical and flexible approach to combine population-and family-based imputation data in large pedigrees. We call this approach “GIGI+BEAGLE”, because it uses imputed data from both GIGI and BEAGLE, although different imputation methods or programs could be used. We evaluate the imputation accuracy of the combined approach via simulation of sequence data on large pedigrees under low and high LD patterns. In addition, we extend the SKAT-RC test to family-based designs (famSKAT-RC), we evaluate its statistical performance, and also the performance of two other association tests: 1) famSKAT [Chen, et al. 2013; Schifano, et al. 2012], and an extension of CMC (Combined Multivariate Collapsing [Li and Leal 2008]) that we propose for family data (famCMWS; Combined Multivariate Weighted Sum). Furthermore, we show a considerable gain of power using imputed data from the combining approach, and also using the famSKAT-RC test, for a variety of scenarios. We implemented famSKAT-RC in R, based on the source code of famSKAT [Chen, et al. 2013] and SKAT [Wu, et al. 2011], and GIGI+BEAGLE in a C program. The source code of the programs is available at http://faculty.washington.edu/wijsman/software.shtml.

Material and Methods

Imputation

Family-based imputation

We used GIGI [Cheung, et al. 2013] to impute untyped SNPs in pedigree data, proceeding pedigree by pedigree. For a pedigree of size N, suppose that we have dense SNP data (e.g. sequence data) for N_d subjects and sparse SNP data (e.g. 1 SNP each ~0.5 centi-Morgan (cM)) for all subjects. To impute the dense SNP genotypes on the N-N_d subjects, this method starts by using inheritance vector (IV) realizations estimated on the sparse SNP data for all subjects. We used the gl_auto program implemented in MORGAN to obtain these IV realizations [Thompson 2011]. Then, based on these IV realizations, the dense SNP data, the meiotic map, the allele frequencies of the dense SNPs, and the pedigree structure, GIGI calculates the probabilities (p_AA, p_Aa, and p_aa) of the three possible genotypes (AA, Aa, aa), the allelic dosages toward the minor allele “a” (Allelic Dosage = 2 × p_aa + 1 × p_Aa + 0 × p_AA), and the best-guess genotypes for each N-N_d subject at untyped dense SNPs. The mathematical and other details concerning GIGI are described elsewhere [Cheung, et al. 2013]. To provide intuition, recall that GIGI imputes SNPs one by one, ignoring the LD information between them. Its method is based on relating the founder genome labels (FGL) to the corresponding allelic types (A, a) via IBD graphs. FGLs, which represent the IBD pattern, are given by the gl_auto package in MORGAN. In brief, GIGI uses three principles based on inheritance in pedigrees to assign allelic types to FGLs. First, GIGI uses the concept of “phasing” a SNP genotype with respect to a pair of FGLs in an individual [Wijsman 1987]. Phasing in an individual, or equivalently, assigning each of two SNP alleles in an individual to one of the two FGLs in the individual, can occur only when the SNP is homozygous in that individual. This phasing is frequency dependent, with a lower probability of occurrence per individual for SNPs with higher MAF than for SNPs with lower MAF. Second, GIGI uses the information that IBD, as represented by a particular FGL, implies that once an allelic type has been assigned to an FGL anywhere in a pedigree, that allelic type can be assigned to all carriers of that FGL. This results in phasing of heterozygote SNP genotypes to their respective FGLs, when one of the two alleles was previously phased as a homozygote within an individual. Finally, any subjects who share the same pair of FGLs must also share both allelic types, even if the particular allelic types cannot be phased relative to the pair of FGLs. These latter two principles are frequency independent since they depend only on allelic or genotypic IBD.

Population-based imputation

We used BEAGLE [Browning and Browning 2009] to impute untyped SNPs assuming that all pedigree subjects are unrelated. This method uses LD information between SNPs rather than IBD information between subjects. BEAGLE puts all subjects having dense SNP data (Dense SNP Subjects, DSS) across all pedigrees in a first pool, which forms the reference panel, and the subjects that have only sparse SNP data in a second pool. Then, using a general class of hidden Markov models (HMMs), it infers the haplotype phase of both pools’ subjects, and based on the estimates of phased haplotypes of the first pool’s subjects, it imputes the second pool’s subjects at their untyped dense SNPs. For these SNPs, BEAGLE calculates the probabilities of the three possible genotypes (AA, Aa, aa), the allelic dosages, and the best-guess genotypes. In the population-based imputation methods, the density of sparse SNPs and the size of the reference panel (number of DSS) are important factors that influence the imputation accuracy. In general, the imputation accuracy increases with the density of sparse SNPs and the reference panel sample size [Badke, et al. 2013; Pei, et al. 2008]. For data consisting of low density sparse SNPs, like that used for GIGI, BEAGLE is unlikely to be able to accurately impute any untyped SNP. This is because the LD between distant SNPs (~500 Mbp) is generally very low. However, note that unlike GIGI that requires the DSS to be selected from the pedigrees, BEAGLE can use external DSS (e.g., 1000 Genomes Project) and can, therefore, impute variants that are not observed in the sequenced pedigree subjects.

Data combination of GIGI and BEAGLE imputation (GIGI+BEAGLE)

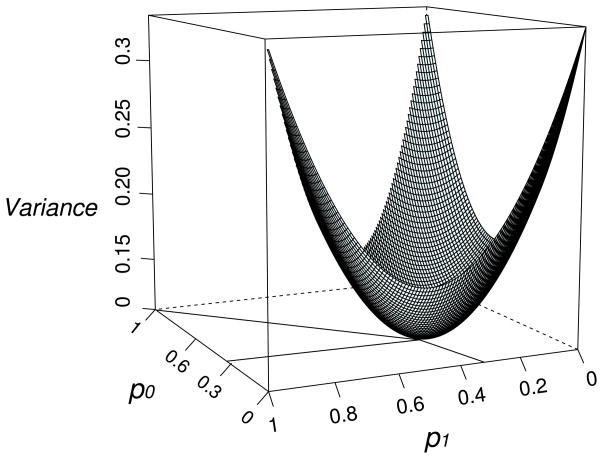
We propose a flexible approach to combine family-based and population-based imputation results. We called our approach here GIGI+BEAGLE because we used GIGI and BEAGLE independently as family- and population-based imputation methods, respectively. Alternative programs and methods could also be used with the expectation of similar results. Our approach is based on a vote strategy between both imputation methods. For every SNP of every individual, we choose the most certain imputation allelic dosage given by either of these methods (GIGI and BEAGLE). The decision criterion of selecting one of the two allelic dosages is based on the highest variance among the corresponding genotype probabilities. The motivation for using this measure comes from the fact that the lowest variance comes from the set of the following probabilities: p₀=0.333, p₁=0.333, and p₂=0.333 (p₀=p_AA, p₁=p_Aa, and p₂=p_aa). This means that the imputation approach cannot choose any one of the three possible genotypes over another. On the other hand, the highest variance results from one of the following sets of probabilities: (p_AA, p_Aa, p_aa) = (0, 0, 1), (0, 1, 0), or (1, 0, 0). These three cases mean that the imputation approach is able to definitively call one of the three possible genotypes. Figure 1 shows all possible probability sets and their variances.

Figure 1.

Joint probabilities of possible genotypes (AA, Aa, aa) and their variances.

Our strategy splits SNPs into two bins: SNPs with rare minor allele (SNPs with MAF≤0.01), which we call “rare” SNPs, and SNPs with common minor allele (SNPs with MAF>0.01), which we call “common” SNPs. For common SNPs, it selects the set of three probabilities having the highest variance between GIGI’s and BEAGLE’s estimates and calculates the corresponding allelic dosage. For rare SNPs, as GIGI clearly has the advantage over BEAGLE because of the low LD between rare and common SNPs, we weight the variance of BEAGLE probabilities of rare SNPs by their imputation accuracy estimates, R², calculated by BEAGLE. In general, the R² values of rare SNPs are very small and usually equal to zero. Therefore, allelic dosages will come from GIGI for the majority of rare SNPs. In the rare case of a tie between GIGI and BEAGLE (equal variances), the allelic dosages come from GIGI for rare SNPs and come from BEAGLE for common SNPs.

We also considered two different approaches to combine data from GIGI and BEAGLE. The first one, which we call G+B+T (GIGI+BEAGLE+Threshold), merges data of rare and common SNPs based on MAF threshold: It extracts allelic dosages of rare SNPs from GIGI and allelic dosages of common SNPs from BEAGLE. The second one, which we call G_S+B (GIGI strict+BEAGLE), first extracts the most certain genotypes (dictated by the pedigree structure) given by GIGI for both rare and common SNPs using very strict imputation calling thresholds (t₁=0.999 and t₂=0.999); that is, only the very confident genotypes are used and the remaining genotypes are set to be missing. Then, it fills in these missing genotypes by their corresponding allelic dosages from the GIGI+BEAGLE approach. G_S+B uses both best-guess genotypes and allelic dosages. If the best-guess genotypes are not accurate, G_S+B may face a decrease of imputation accuracy. This approach is similar to the GAW18 study [Marchani, et al. (in press)] as the authors used strict imputation calling thresholds for GIGI. However, they used the BEAGLE best-guess genotypes rather than allelic dosages, used in our combining approach.

Association analysis

Several association tests have been proposed to deal with rare and common SNPs jointly, such as SKAT/famSKAT [Chen, et al. 2013; Schifano, et al. 2012; Wu, et al. 2011], SKAT-RC [Ionita-Laza, et al. 2013], and CMC [Li and Leal 2008]. The last two tests split rare and common SNPs into two bins and treat them separately via a kernel test (SKAT-RC) and a multiple regression (CMC) framework. The SKAT-RC and CMC tests have been proposed for population-based designs. We propose extensions of these two tests to family-based designs, famSKAT-RC and famCMWS. In famCMWS, rare SNPs are collapsed into a mega-variable, which is treated as single variable with common SNPs, each separately, as fixed effects. However in famSKAT and famSKAT-RC, all SNPs are treated separately and considered as random effects. All these tests account for family relationships through a random effect structured by the kinship matrix. Unlike famSKAT and famSKAT-RC, famCMWS suffers when the effects of associated SNPs are in opposite directions. However, we do not consider this scenario in our simulations because it has been widely discussed in the literature and SKAT-type tests are generally expected to outperformed the burden-type tests [Chen, et al. 2013; Schifano, et al. 2012; Wu, et al. 2011].

We performed association analysis on a quantitative trait, only, using four tests: famSKAT, famSKAT-RC, famCMWS, and famSKAT-B, which is similar to famSKAT but with rare SNPs collapsed as in famCMWS. We used this test as a parallel comparison with famCMWS (with same variables in the model). We compared these four tests, in the sequence data, while taking only associated SNPs in the analysis into account, or including both associated and non-associated SNPs in the analysis. In the different imputation datasets, we only used famCMWS taking only associated SNPs in the analysis into account. Performing the other tests would lead to the same conclusions.

Before describing the models, we introduce the following notation:

Y is the vector of quantitative trait values of all N individuals;

R_(N×r) = [w_R,1R₁ … w_R,jR_j … w_R,rR_r] and C_(N×c) = [w_C,1C₁ … w_C,jC_j … w_C,cC_c] are the weighted genotype matrices of the N individuals at the r and c rare and common SNPs in a region of interest (e.g. gene), where genotypes are coded as the number (or the expected/estimated number in imputation) of copies of minor alleles. The variables w_R,. and w_C,. are the weights for rare and common SNPs, respectively, where $\sqrt{w_{R,j}}~\mathit{Beta}(1,25)$ [Wu, et al. 2011] and $\sqrt{w_{C,j}}~\mathit{Beta}(0.5,0.5)$ [Ionita-Laza, et al. 2013];

X_(N×p) = [X₁ … X_j … X_p] is the matrix of p covariates; $u=(u_1,\dots ,u_N)~N(0,{\sigma }_g^2\mathit{\Phi })$ is the vector of individual specific random effects where ${\sigma }_g^2$ is the genetic variance, Φ_(N×N) is a matrix of twice the coefficient of kinship between pairs of individuals, and I_(N×N) is the identity matrix. Note that the use of twice the coefficient of kinship is important if one want to correctly estimate the value of ${\sigma }_g^2$. In our analysis, it is just a scaling parameter;

and finally, $\epsilon =({\epsilon }_1,\dots ,{\epsilon }_N)~N(0,{\sigma }_e^{2}I)$ is the vector of residual errors where ${\sigma }_e^2$ is the residual variance.

Combined Multivariate Weighted Sum approach accounting for family relationship: “famCMWS”

The famCMWS model is

$$Y=X\alpha +{\beta }_r\sum _{j=1}^r\sqrt{w_{R,j}}{R}_j+C{\beta }_c+u+\epsilon$$

where: α_(p,1), β_r(1,1), and β_c(c,1) are the fixed effect coefficients. To test the association between the trait and the region of interest, we used the log likelihood ratio test (LRT) to compare the two models M₀: Y = Xα + u + ε and $M_1:Y=X\alpha +{\beta }_r{\sum }_{j=1}^r\sqrt{w_{R,j}}{R}_j+C{\beta }_c+u+\epsilon$. The test statistic is twice the difference of the two models’ likelihoods: $T=-2[ln(L_0)-ln(L_1))~{\chi }_{(c+1)}^2$, where L₀ and L₁ are the likelihoods of M₀ and M₁, respectively. This test corresponds to the null hypothesis H₀:β_r = 0, β_c = 0. In real data analysis, if this test gives significant results, we should consider testing H₀:β_r = 0, or H₀:β_c = 0 in order to determine if the test is driven by rare or common SNPs alone.

Sequence Kernel Association Test accounting for family relationship: “famSKAT-RC”

The famSKAT-RC model is

$$Y=X\alpha +R{\beta }_r+C{\beta }_c+u+\epsilon$$

where β_r(r,1) and β_c(c,1) are the vectors of random effect coefficients of rare and common SNPs, respectively, with E(β_r) = 0, E(β_c) = 0, Var(β_r) = ϕτ, Var(β_c) = (1 − ϕ)τ, τ is a variance component, and ϕ is the part of the variance explained by rare SNPs. The log-likelihood is

$$l=C-\frac{1}{2}log\mid V\mid -\frac{1}{2}{(Y-X\widehat{\alpha })}^{\prime }{V}^{-1}(Y-X\widehat{\alpha })$$

where $V=\tau \varphi R{R}^{\prime }+\tau (1-\varphi )C{C}^{\prime }+{\sigma }_g^2\mathit{\Phi }+{\sigma }_e^{2}I=\mathit{Var}(Y)$. The first derivative of the log-likelihood respect with τ is

$$\frac{\partial l}{\partial \tau }=-\frac{1}{2}\text{tr}\left(V^{-1}(\varphi R{R}^{\prime }+(1-\varphi )C{C}^{\prime })\right)+\frac{1}{2}{(Y-X\alpha )}^{\prime }{V}^{-1}(\varphi R{R}^{\prime }+(1-\varphi )C{C}^{\prime })V^{-1}(Y-X\widehat{\alpha })$$

Testing the null hypothesis of β_r = β_c = 0 is equivalent to testing the null hypothesis of τ = 0. Under this null hypothesis, $\widehat{V}={\sigma }_g^2\mathit{\Phi }+{\sigma }_e^{2}I$, and the score test statistic is written as:

$$\begin{array}{c}Q={(Y-X\widehat{\alpha })}^{\prime }{\widehat{V}}^{-1}(\varphi R{R}^{\prime }+(1-\varphi )C{C}^{\prime }){\widehat{V}}^{-1}(Y-X\widehat{\alpha })\\ =\varphi [{(Y-X\widehat{\alpha })}^{\prime }{\widehat{V}}^{-1}R{R}^{\prime }{\widehat{V}}^{-1}(Y-X\widehat{\alpha })]+(1-\varphi )[{(Y-X\widehat{\alpha })}^{\prime }{\widehat{V}}^{-1}C{C}^{\prime }{\widehat{V}}^{-1}(Y-X\widehat{\alpha })]\\ =\varphi Q_{\mathit{rare}}+(1-\varphi )Q_{\mathit{common}}.\end{array}$$

It is straightforward to see that this test is equivalent to the original famSKAT for rare SNPs if ϕ = 1 or for common SNPs if ϕ = 0. In our analysis, we compared the performance of famSKAT-RC for three different values of ϕ:0.3, 0.5, and $\frac{\text{SD}(Q_{\mathit{rare}})}{\text{SD}(Q_{\mathit{rare}})+\text{SD}(Q_{\mathit{comon}})}$. The test using the last value was used by [Ionita-Laza, et al. 2013] and yielded greater power than the test that uses a grid of different values ϕ(0, 0.25, 0.5, 0.75, 1).

The statistic Q follows a sum of chi-square distributions with one df each [Zhang and Lin 2003]:

$$Q~\sum _i^q{\lambda }_i{\chi }_{1,i}^2;$$

where λ_is are the eigenvalues of the matrix $P^{\frac{1}{2}}(\varphi R{R}^{\prime }+(1-\varphi )C{C}^{\prime })P^{\frac{1}{2}}$, P = V̂⁻¹ − V̂⁻¹X(XV̂⁻¹X′)⁻¹X′V̂⁻¹. P-values can be estimated analytically using the Davies approximation [Lee, et al. 2012; Wu, et al. 2011]. Note that the nuisance parameter ρ used in [Jiang and McPeek 2014; Lee, et al. 2012] to combine the advantages of both burden and kernel tests was not implemented in our model and will be implemented in future studies.

Simulation

We simulated sequence data on a large collection of extended pedigrees extracted from an Alzheimer’s disease cohort under study at the University of Washington. These pedigrees are therefore representative of what may be found in a real study. We considered five datasets: 1) D1: All subjects are sequenced; 2) D2: 20% of subjects are sequenced and the remaining subjects, which have sparse SNP data, are imputed using GIGI (same strategy of [Saad and Wijsman 2014]); 3) D3: This dataset is the same as the previous one except that imputation was carried out using BEAGLE; 4) D4, D5, and D6: These three datasets are the combination of D2 and D3 using the GIGI+BEAGLE, G+B+T, and G_S+B approaches, respectively.

Simulated Sequence Data

We used the same simulation strategy used in a previous study [Saad and Wijsman 2014] to obtain 100 semi-realistic sequence datasets that mimic the 1000 Genomes Project sequence data [Abecasis, et al. 2010]. Briefly, we simulated 20,000 haplotypes for a region of 10 Mbp. In the center of this region, we considered a gene of 30 Kbp length (313 SNPs). We considered two LD pattern scenarios: LowLD and HighLD. From the pool of 20,000 haplotypes, we started by randomly selecting haplotypes, without replacement, for the unrelated founders. Then, we passed the haplotypes down through the generations (the number of generations varies between three and five) using a recombination rate of 1% per cM per meiosis. We repeated this last step 100 times for each LD pattern to obtain 100 sequence datasets.

We considered 40 pedigrees with mean size 30 subjects, and sizes ranging from 20 to 53 subjects. The pedigrees we considered contain a total of 1197 subjects (384 founders).

Simulated Phenotype

Type 1 Error and Power simulation

For each simulated sequence dataset, we simulated 100 quantitative traits under the null hypothesis of no association. We fitted the model Y = ε where ε follows a multivariate normal distribution N(0, Σ), with Σ = h²Φ + (1 − h²)I. We fixed the genetic variance due to polygenic effects as ${\sigma }_g^2=1$ and the residual variance as ${\sigma }_e^2=1$, so the heritability is $h^2=\frac{{\sigma }_g^2}{{\sigma }_g^2+{\sigma }_e^2}=0.5$. This model has genetic variation defined by the pedigree structure but not by the gene.

Under the alternative hypothesis of association, we simulated 100 quantitative traits for each simulated sequence dataset by fitting the model: Y = G^Aβ^A + ε where β^A is the vector of effect sizes of the “A” associated SNPs, G^A is the (N × A) matrix of their genotypes and ε is defined above (type 1 error simulation). The effect sizes of the associated SNPs were determined by the function ${\beta }_j^A=\sqrt{\frac{v_{\mathit{total}}^A/A}{2\times {\mathit{MAF}}_j\times (1-{\mathit{MAF}}_j)}}$, where MAF_j is the minor allele frequency of the associated SNP j estimated in the generated sequence data, and $v_{\mathit{total}}^A$ is the total additive variance of all associated SNPs combined. The genetic variation of this model is defined by both pedigree structure and associated SNPs. In our simulation, we set the total additive variance to 1%, so 99% of the genetic variance is not explained by SNPs in the gene. We tuned the value of the total additive variance in such a way that the power of the association test is neither very low nor very high to maximize power differences among the methods. We randomly selected associated SNPs from the list of rare and common SNPs in the gene and we varied their numbers as 10 and 20. We also varied the proportion of rare (f_r) and common (f_c) associated SNPs among all associated SNPs as (f_r, f_c) = (0.7, 0.3) and (0.5, 0.5). We also added non-associated SNPs in the model for some settings. We set the number of non-associated SNPs (U) as the double of the number of associated SNPs (U=2A), using the same proportions of common SNPs, f_c. Note that all associated SNPs have the same effect directions.

We estimated both type 1 error and power rates at threshold α as the proportion of replicates for which the p-value of the association test is lower than α.

Imputation Analysis

Sparse and dense SNPs for GIGI

Prior to imputation for each genetic dataset, we used the program gl_auto in MORGAN (http://www.stat.washington.edu/thompson/Genepi/MORGAN/Morgan.shtml) [Thompson 2011] to obtain a set of 1000 IVs, at the positions of the sparse SNPs, realized from the joint distribution of SNP genotypes given the pedigree and observed data. The sparse SNP set consisted of 20 SNPs, approximately equally distant (one SNP is each 0.5 Mb ~0.5 cM), in linkage equilibrium (LE), highly informative (MAF>0.4), and typed on all subjects. The dense SNP dataset is limited to the considered gene, which contains 313 SNPs.

Sparse and dense SNPs for BEAGLE

For BEAGLE, the sparse SNP (tag SNP) dataset should be denser than the sparse SNP dataset used for GIGI in order to achieve good imputation accuracy. We limited the dense SNP dataset to the gene region plus 250 Kbp up and downstream (3599 SNPs). Among these SNPs, we used the HapBlock [Nicolas, et al. 2006] software in both LowLD and HighLD pattern datasets to select the list of tag SNPs. This software gives a sorted list of the most informative SNPs. We chose the first 400 SNPs, which yielded a density of one SNP every ~1.3 Kbp. Increasing this density would likely improve the imputation accuracy, and hence the power of association. However, our conclusions do not depend on this particular choice of SNP density. Note that during phasing, BEAGLE completely ignores relationships among individuals and only uses the LD information. Including the pedigree structure information would add extra information and improve the phasing. BEAGLE can use trio samples to improve the phasing but not the complete pedigree structure. The influence of doing this on the accuracy of imputation needs evaluation in further studies.

Dense SNP Subjects (DSS) selection

Although the selection of DSS is of great importance to absolute power, as discussed earlier [Saad and Wijsman 2014], we simply selected d = 20% of subjects, at random, from each pedigree to be the DSS, rounding up the number of selected subjects. This led to a selection of 240 different subjects in each of the 100 simulated sequence datasets. A good selection of DSS is not the focus of our study and the selection strategy we conducted should not affect our conclusions. Nonetheless, by selecting different sets of subjects in each replicate of our simulation datasets, we covered the space of possible combinations of DSS.

Results

Imputation accuracy

Our aim is to compare the imputation accuracy between three main approaches: GIGI, BEAGLE, and GIGI+BEAGLE. We used the correlation estimate between the allelic dosages and the true genotypes as a measure of imputation accuracy. Correlation estimates may not be efficient for measuring imputation accuracy, especially for rare SNPs. However, our aim here is not to evaluate the imputation accuracy per se, but to compare it between different approaches. Four correlation values were attributed to every SNP. The first three values are the correlations between the true genotypes and the allelic dosages obtained by 1) GIGI (i.e. ρ_GIGI = cor(True, GIGI)), 2) BEAGLE (i.e. ρ_BEAGLE = cor(True, BEAGLE)), and 3) our approach GIGI+BEAGLE (i.e. ρ_GIGI+BEAGLE = cor(True, GIGI + BEAGLE)). The last value is the greater correlation of GIGI’s and BEAGLE’s correlations (i.e. MAX: ρ_MAX = max(ρ_GIGI, ρ_BEAGLE)). These four correlation values are the correlation averaged across the 100 simulated datasets. We compared these four correlation values for rare and common SNPs, separately. First, we compared GIGI to BEAGLE to show the best performance of both approaches for rare and common SNPs. Second, we compared GIGI+BEAGLE to GIGI and BEAGLE separately. Finally, we compared GIGI+BEAGLE and MAX to show the relative performance of our approach to the best (unknown in real data) of GIGI and BEAGLE. All of these comparisons were made for the two LD patterns (i.e. LowLD and HighLD).

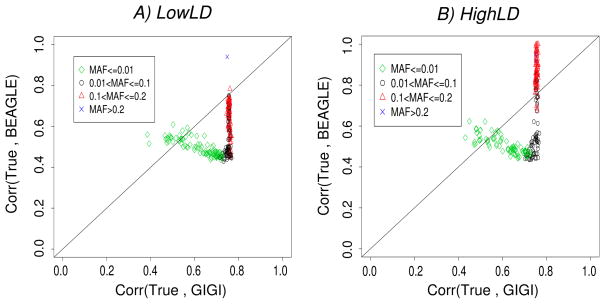
GIGI versus BEAGLE (Figure 2)

Figure 2.

Correlation between allelic dosages obtained by GIGI and the true genotypes (x-axis) versus correlation between allelic dosages obtained by BEAGLE and the true genotypes (y-axis), for different bins of MAFs: A) LowLD pattern, B) HighLD pattern.

We observed that GIGI had greater correlations with the truth than BEAGLE for almost all SNPs (even for common SNPs) under the LowLD pattern (Figure 2A). However, for the HighLD pattern, BEAGLE outperformed GIGI for SNPs with MAF greater than 0.1. For the majority of the remaining SNPs, GIGI appeared to be better (Figure 2B).

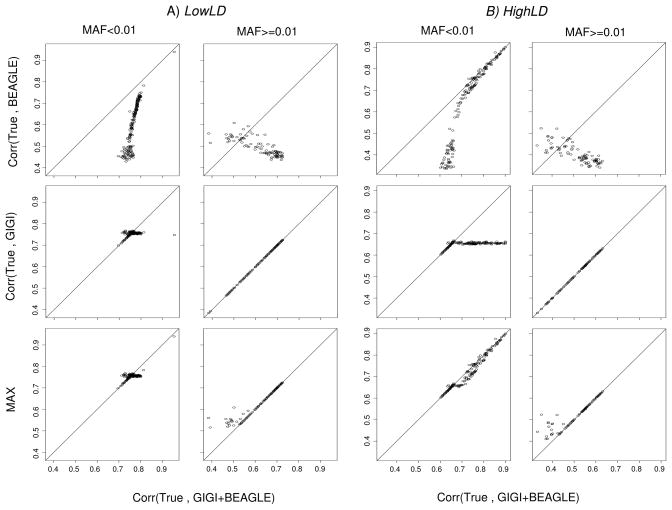
GIGI+BEAGLE versus BEAGLE and GIGI (First and second row of Figure 3)

Figure 3.

Correlation between allelic dosages obtained by GIGI+BEAGLE and the true genotypes (x-axes) versus correlation between allelic dosages obtained by: BEAGLE (first row figures), GIGI (second row figures), and the MAX between the correlations obtained by GIGI and BEAGLE (third row figures) with the true genotypes (y-axes). A) LowLD pattern, B) HighLD pattern. Left part of every LD pattern column figures: MAF>0.01; Right part of every LD pattern column figures: MAF<=0.01.

Interestingly, for both LowLD and HighLD patterns, GIGI+BEAGLE performed better or at least similar to BEAGLE for common SNPs (First row of Figure 3A and 3B). The better imputation accuracy of GIGI+BEAGLE was more striking for the LowLD pattern. This is expected because BEAGLE’s performance decreases with decreasing LD. Moreover for common SNPs, GIGI+BEAGLE shows greater imputation accuracy than does GIGI alone, especially for the HighLD pattern (Second row of Figure 3B). On the other hand for rare SNPs, GIGI+BEAGLE was better than BEAGLE for the majority of SNPs but performed similarly to GIGI, which indicates that the rare SNPs’ allelic dosages of GIGI+BEAGLE come from GIGI.

GIGI+BEAGLE versus MAX (Third row of Figure 3)

More importantly, we observed that GIGI+BEAGLE had an advantage even over the best of GIGI and BEAGLE for common SNPs (LowLD and HighLD). However, the MAX approach was slightly more advantageous for a few rare SNPs. These are SNPs imputed by BEAGLE from outside information that did not segregate down through the generations in the pedigree(s).

Our previous correlation results showed that our approach of combining imputation results across population and family data tends to improve the accuracy of imputation, regardless of the allele frequency spectrum and the LD patterns. In the next section, we investigate the gain of power of association tests using our approach’s combined data. Indeed, we compare the power of using data from GIGI+BEAGLE to that of using data from GIGI, BEAGLE, and the true simulated sequence data.

Association Analysis

We performed association analysis on the following datasets described above: D1 (Sequence), D2 (GIGI), D3 (BEAGLE), D4 (GIGI+BEAGLE), D5 (G+B+T), and D6 (G_S+B). We estimated the type 1 error and power rates at a threshold of α=0.01.

Type 1 Error Results

Over all scenarios we considered, type 1 error rates for all tests were well controlled. Under the LowLD pattern, the type 1 error rates of famSKAT-RC, famCMWS, famSKAT, and famSKAT-B including only associated SNPs in sequence data are shown in Table 1 and are very close to the target α=0.01. Type 1 error rates of famCMWS including only associated SNPs in imputation data under the LowLD pattern are shown in Table 2. Under the HighLD pattern, the corresponding results are shown in Table S1 and Table S2 in supplementary material. Finally, the results for association tests including both associated and non-associated SNPs in sequence data are shown in Table S3 and Table S4 in supplementary material for both LD patterns.

Table 1.

Type I error of of association tests: famSKAT-RC, famCMWS, famSKAT, and famSKAT-B under the LowLD pattern in the sequence data. A is the number of associated SNPs and f_c is the proportion of common SNPs.

A	fc	famSKAT-RC			famCMWS	famSKAT-B	famSKAT
		ϕ =0.5	ϕ =0.3	ϕ = $
10	0.3	0.0085	0.0082	0.0087	0.0099	0.0100	0.0100
	0.7	0.0100	0.0087	0.0094	0.0114	0.0086	0.0098
20	0.3	0.0092	0.0084	0.0090	0.0092	0.0106	0.0123
	0.7	0.0094	0.0113	0.0096	0.0110	0.0101	0.0094

^$ϕ = sd(Qrare)/(sd(Qrare)+sd(Qcommon))

Table 2.

Type I error of famCMWS under the LowLD pattern in the imputation data. A is the number of associated SNPs and f_c is the proportion of common SNPs.

A	fc	GIGI	BEAGLE	GIGI+BEAGLE	G+B+T	G_S+B
10	0.3	0.0099	0.0108	0.0082	0.0115	0.0113
	0.5	0.0123	0.0096	0.0118	0.0096	0.0112
20	0.3	0.0098	0.0110	0.0094	0.0113	0.0099
	0.5	0.0099	0.0117	0.0098	0.0110	0.0111

Power Results

We show our power results in two sections. The first one is “Comparison of association tests in sequence data”, in which we compare the power of famSKAT-RC, famCMWS, famSKAT, and famSKAT-B. For famSKAT-RC, we use a value of ϕ = 0.5 for all our comparisons, as we observed a slightly greater power using this value (Figure S1 in supplementary material). The second section is “famCMWS in imputation data”, in which we compare the power of famCMWS achieved using the different imputation datasets.

1) Comparison of association tests in sequence data

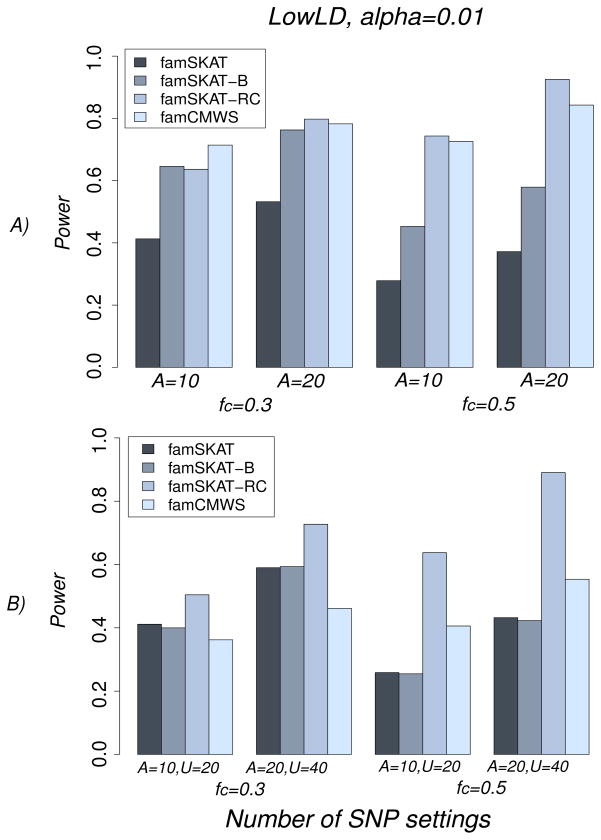
We started first by only including associated SNPs in the association model. Our results, under the LowLD pattern (Figure 4A), showed that famSKAT-RC was the most powerful test for all scenarios we considered, except for A=10 and f_c=0.3 where famSKAT-B and famSKAT-RC were essentially equivalent and fell between famSKAT and famCMWS. The second most powerful test was famCMWS. The original famSKAT was the least powerful. The difference of power between famSKAT-RC and famCMWS increased with the number of common SNPs: for three, five, six, and ten common SNPs, the difference of power increased from −0.07, to 0.01, 0.02, and to 0.09. As expected, famSKAT-B performed better than famSKAT because it collapses rare SNPs (associated risk SNPs), and hence this test was less penalized in this setting by the increasing df. Note that this result would no longer be true if protective and risk variants were included in the model. Interestingly, famCMWS performed better than famSKAT and famSKAT-B. The explanation of this result is that the burden tests are known to perform better when only associated SNPs are included in the model and have the same effect directions. However, including non-associated (and even protective) rare SNPs in the models would most likely decrease the power of famCMWS and famSKAT-B (as suggested in the literature [Chen, et al. 2013; Ionita-Laza, et al. 2013; Schifano, et al. 2012; Wu, et al. 2011]), but not as much as for famSKAT. Therefore, we evaluated the influence of including non-associated SNPs in the model on the power. Here, the power of famSKAT-RC, famCMWS, and famSKAT-B decreased, under the LowLD pattern (Figure 4B). FamCMWS and then famSKAT-B, were the most affected by the inclusion of non-associated SNPs. However, famSKAT was more robust: the power did not change much for A=10 and it increased for A=20. More importantly, famSKAT-RC substantially outclassed all other tests. The smallest and greatest differences of power between famSKAT-RC and the second most powerful test across all scenarios were 0.09 (for A=10, U=20, f_c=0.3) and 0.34 (for A=20, U=40, f_c=0.5), respectively. For the HighLD pattern, we observed the same trends (results not shown). Note that the weighting schemes used in the association tests may be of great importance and influence the power, especially when we study both common and rare SNPs jointly (results not shown). Therefore, this needs to be investigated more in future studies.

Figure 4.

Power of famSKAT, famSKAT-B, famSKAT-RC, and famCMWS in the sequence data, under the LowLD pattern, for the different settings of number of associated and non-associated SNPs and the proportion of common SNPs among them; A) For a model with associated SNPs only: A=10, f_c=0.3; A=10, f_c=0.5; A=20, f_c=0.3; and A=20, f_c=0.5; B) For a model with associated and non-associated SNPs: A=10, U=20, f_c=0.3; A=10, U=20, f_c=0.5; A=20, U=40, f_c=0.3; and A=20, U=40, f_c=0.5, where f_c is the proportion of common SNPs.

In the following section, we show the power results of famCMWS with a model including only associated SNPs, because the other tests with the other methods led to the same conclusions (results not shown), and also, famSKAT-RC was more computationally intensive.

2) famCMWS in imputation data

Figure 5 shows the power results of all imputation designs and the power achieved from using sequence data (all subjects are sequenced; D1). The D1 dataset is expected to give the greatest power and we consider it as our baseline comparison.

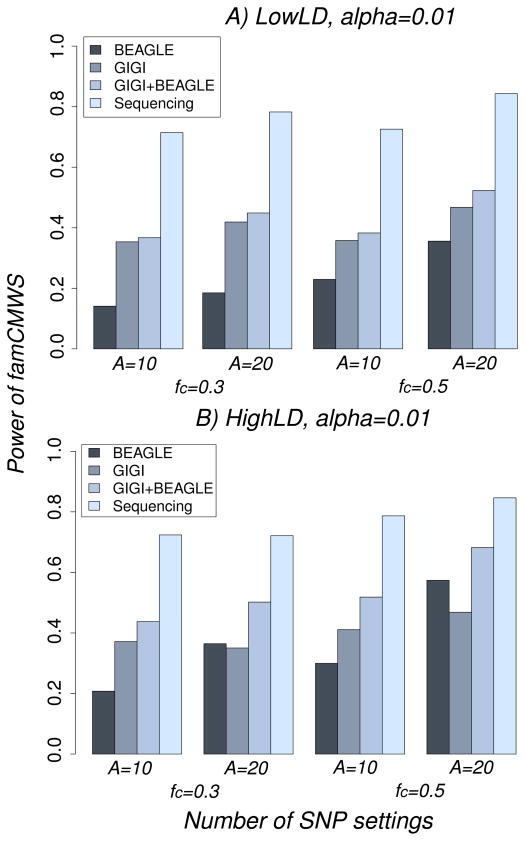
Figure 5.

Power of famCMWS for the different imputation and the sequence data, for a model with associated SNPs only, for the different settings of number of associated SNPs and the proportion of common SNPs among them: A=10, f_c=0.3; A=10, f_c=0.5; A=20, f_c=0.3; and A=20, f_c=0.5, where f_c is the proportion of common associated SNPs. A) LowLD pattern; B) HighLD pattern.

For the LowLD pattern, we observed that GIGI and GIGI+BEAGLE were substantially more powerful than BEAGLE for all numbers of associated SNPs (Figure 5A). For example, for A=20 and f_c=0.3, the power of GIGI, GIGI+BEAGLE, and BEAGLE was 0.42, 0.45, and 0.18, respectively (most of the advantage of GIGI+BEAGLE is derived from GIGI). This result is congruent with our imputation accuracy results, in which we observed that GIGI had more accuracy than BEAGLE for almost all SNPs under the LowLD pattern. Interestingly, our approach GIGI+BEAGLE produced (slightly) better power compared to GIGI. This suggests that although BEAGLE had poor performance in the LowLD pattern, GIGI+BEAGLE resulted in more information than GIGI alone did. This is consistent with the results in figures 3, which showed a few SNPs with low MAF that were better imputed by BEAGLE than GIGI, probably because no transmission information in the pedigrees was obtained by the choice of sequenced subjects.

On the other hand, under the HighLD pattern (Figure 5B), the difference of power between BEAGLE and GIGI (D) depends on the number of common SNPs in the model: for three, five, six, and ten common SNPs, D increased from −0.16 to −0.11, 0.01, and to 0.1. The explanation of this observation is that BEAGLE outperformed GIGI for common SNPs, so BEAGLE is better when the number of common SNPs increased. More importantly, GIGI+BEAGLE was still better than both of GIGI and BEAGLE for all scenarios.

All these results show that the gain of power using combined family- and population-based imputation via GIGI+BEAGLE results in a consistent increase of power of association testing.

LD pattern

As the amount of LD is a major factor for the success of BEAGLE’s imputation, it is important to evaluate the behavior of association tests using the combined data for different LD patterns. First, we did not observe any influence of LD on the power of association testing using either sequencing data or GIGI imputation data (results not shown), which is in agreement with what has been shown in the literature [Saad and Wijsman 2014]. This trend did not hold for BEAGLE and GIGI+BEAGLE (Figure S2, S3 in supplementary material). The power of association tests using these approaches increased when the LD between SNPs increased. This is expected because BEAGLE depends on the LD to impute untyped SNPs and GIGI+BEAGLE uses BEAGLE imputation data.

GIGI+BEAGLE versus alternative combinations

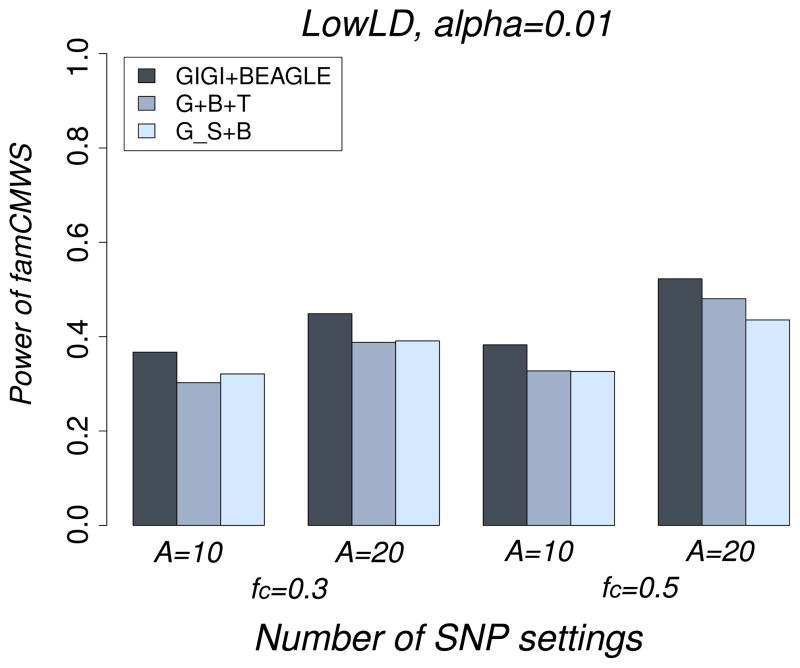
Finally, we compared GIGI+BEAGLE to G+B+T and G_S+B. GIGI+BEAGLE consistently performed better than the other approaches for both LowLD (Figure 6) and HighLD (Figure S4) patterns, as well for all other considered scenarios of the number of associated SNPs and the ratio of common SNPs among them. The result of GIGI+BEAGLE being better than G_S+B is initially counter-intuitive. We would expect that G_S+B would give results that were at least similar to those from GIGI+BEAGLE. After investigating this result, we found that the reason for the decrease in performance with the G_S+B approach is that even the very confident genotypes dictated by the pedigree were not always correct, especially for common SNPs.

Figure 6.

Power of famCMWS for the different combined imputation data (GIGI+BEAGLE, G+B+T, and G_S+B), under the LowLD pattern, for a model with associated SNPs only, for the different settings of number of associated SNPs and the proportion of common SNPs among them: A=10, f_c=0.3; A=10, f_c=0.5; A=20, f_c=0.3; and A=20, f_c=0.5, where f_c is the proportion of common associated SNPs.

Discussion

The involvement of rare and common variants, jointly or separately, in the etiologies of complex traits is a plausible hypothesis [Curtis 2012; Gibson 2011; Iyengar and Elston 2007]. Family-based association studies represent an attractive approach to study these two types of variants. However, even with the use of this design, large sample sizes are still needed to achieve good power, especially for rare variants. Moreover, to genotype these variants, the use of sequencing techniques are required. Despite decreasing sequencing costs, sequencing (Whole Genome and Exome Sequence (WGS/WES)) large family datasets (thousands of samples) is still prohibitive. Nonetheless, the pseudo-sequencing strategy [Saad and Wijsman 2014], based on imputation methods, makes the large family-based GWAS more affordable.

The imputation method GIGI [Cheung, et al. 2013] can handle large (and possibly complex) pedigrees (>100 subjects per pedigree). Despite the ability of GIGI to accurately impute rare variants, it does less well with common variants, particularly when dense framework data are available [Cheung, et al. 2013]. Here, population-based imputation methods, which use LD information and the dense framework panel of SNPs to guide imputation, are more suitable for common variant imputation. Several population-based imputation methods exist and perform very well for common variant imputation (MACH [Li, et al. 2006], IMPUTE [Marchini, et al. 2007], BEAGLE [Browning and Browning 2009]). In our study, we proposed a simple flexible approach to combine population- and family-based imputation data in large pedigrees. The main aim of our approach was to improve the imputation accuracy of both rare and common variants and jointly study them via association analysis. Our results showed a substantial and consistent increase of power using combined imputation approaches compared to the use of population- or family-based imputation data alone. The approach we propose is a straightforward two-step approach and has the advantage that it can be immediately applied to combining results from any such pair of programs. Other approaches may also be developed in the future to combine imputation data from more than one approach, or to incorporate ideas from population-based imputation into pedigree-based imputation. However, such approaches will be challenging to implement, and are clearly the topic of future work.

Our combining approach is based on allelic dosages. The combining approach that uses the most confident genotypes given by GIGI (G_S+B), dictated imputation from pedigree information, led to a decrease of power compared to the use of allelic dosages. Possible explanations of such a result include the fact that sampled inheritance vectors, even with 1000 realizations, might not always capture all possible inheritance vectors, and low-probability genotypes (e.g., homozygotes for the minor allele) may never be sampled. This suggests that the use of best-guess/most confident genotypes is advised neither in combining imputation data nor in downstream association analysis. Use of the allelic dosages instead, which take into account the imputation uncertainty, gives better imputation accuracy and hence greater power of association tests.

Several association tests have been proposed to deal with rare and common variants jointly, such as CMC [Li and Leal 2008] and SKAT/famSKAT [Chen, et al. 2013; Schifano, et al. 2012; Wu, et al. 2011]. Recently, a new kernel test, SKAT-RC, has been proposed for data of unrelated subjects [Ionita-Laza, et al. 2013]. This test outperformed the existing tests for many scenarios and simulation settings. We extended this test to family-based designs (famSKAT-RC) along with the CMC test (famCMWS). Our results showed that famSKAT-RC also outperformed all tests under the conditions we considered so far (famCMWS, famSKAT). The model used by famSKAT-RC splits variants into two classes (rare and common) using an arbitrary choice of MAF. However, when the spectrum of associated variant frequencies varies widely, moving between rare, uncommon, and common variant categories (and maybe more categories), considering a model of famSKAT-RC with a few extra classes of variants might yield better power and it is worth more investigation in the future. In addition, it is important to investigate thoroughly the influence of pedigree structure and size along with the number of rare and common associated and non-associated variants, together with the mix of protective and risk effects.

In summary, in our study, we showed the benefit of combining population- and family-based imputation data in a simple approach that is practical and useful for use on real data analysis. We also showed that famSKAT-RC generally has greater power than several other existing tests we considered, which encourages considering it in future family-based GWAS, hunting for rare and common variants jointly. The source code for famSKAT-RC, implemented in R, and of GIGI+BEAGLE, implemented in a C program, is available at http://faculty.washington.edu/wijsman/software.shtml.

Supplementary Material

Fig S1. Figure S1.

Power of famSKAT-RC in sequence data for different values of ϕ, under the LowLD pattern, for a model with associated SNPs only, for the different settings of number of associated SNPs and the proportion of common SNPs among them: A=10, f_c=0.3; A=10, f_c=0.5; A=20, f_c=0.3; and A=20, f_c=0.5, where f_c is the proportion of common associated SNPs.

Fig S2. Figure S2.

Power of famCMWS in imputation data given by BEAGLE, for a model with associated SNPs only, for the different LD patterns and the settings of number of associated SNPs and the proportion of common SNPs among them: A=10, f_c=0.3; A=10, f_c=0.5; A=20, f_c=0.3; and A=20, f_c=0.5, where f_c is the proportion of common associated SNPs.

Fig S3. Figure S3.

Power of famCMWS in imputation data given by GIGI+BEAGLE, for a model with associated SNPs only, for the different LD patterns and the settings of number of associated SNPs and the proportion of common SNPs among them: A=10, f_c=0.3; A=10, f_c=0.5; A=20, f_c=0.3; and A=20, f_c=0.5, where f_c is the proportion of common associated SNPs.

Fig S4. Figure S4.

Power of famCMWS for the different imputation combined data (GIGI+BEAGLE, G+B+T, and G_S+B), under the HighLD pattern, for a model with associated SNPs only, for the different settings of number of associated SNPs and the proportion of common SNPs among them: A=10, f_c=0.3; A=10, f_c=0.5; A=20, f_c=0.3; and A=20, f_c=0.5, where f_c is the proportion of common associated SNPs.