Figure 1.

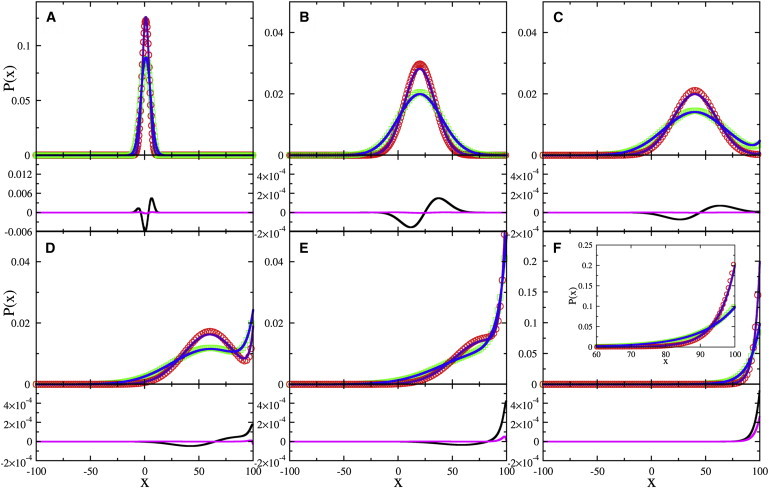
Evolution of P(x,t) starting from the δ-distribution P(x,0) = δ(x). The bacterial profiles of the two-step (blue line) and three-step (purple line) swimmers, calculated based on Eq. 18 at reduced times t/t_v = 0.01, 0.2, 0.4, 0.6, 0.8, and 2, are plotted in panels A–F, respectively. Here the chemoattractant concentration increases linearly along x, t_v (≡ L/v_d) 10⁴Δt, and Δt = 1 is the computation step. As seen, the steady-state exponential profiles are formed at t/t_v ≃ 2. (Green squares and red circles) Numerical solutions for Eqs. 3 and 4, and 10–13, respectively. (F, inset) Close-up for the steady-state profiles, where colored symbol and line designations are the same as above. Beneath each PDF, the first two terms $\left(v^2/2k_0\right)\left({\partial }^{2}P/\partial x^2\right)-v\left(\Delta k/k_0\right)\left(\partial P/\partial x\right)$ (black lines) and the last term $1/2\left(\partial /\partial x\right)\delta J_{\text{cw}}$ (magenta lines) on the right-hand side of Eq. 16 are plotted based on the numerical solutions. As seen, the extra flux term is significant only for late times. However, the analytic calculation without this term still yields a quantitatively good result, as demonstrated in panel F (inset). To see this figure in color, go online.