Abstract
The error threshold of replication limits the selectively maintainable genome size against recurrent deleterious mutations for most fitness landscapes. In the context of RNA replication a distinction between the genotypic and the phenotypic error threshold has been made; where the latter concerns the maintenance of secondary structure rather than sequence. RNA secondary structure is treated as a proxy for function. The phenotypic error threshold allows higher per digit mutation rates than its genotypic counterpart, and is known to increase with the frequency of neutral mutations in sequence space. Here we show that the degree of neutrality, i.e. the frequency of nearest-neighbour (one-step) neutral mutants is a remarkably accurate proxy for the overall frequency of such mutants in an experimentally verifiable formula for the phenotypic error threshold; this we achieve by the full numerical solution for the concentration of all sequences in mutation-selection balance up to length 16. We reinforce our previous result that currently known ribozymes could be selectively maintained by the accuracy known from the best available polymerase ribozymes. Furthermore, we show that in silico stabilizing selection can increase the mutational robustness of ribozymes due to the fact that they were produced by artificial directional selection in the first place. Our finding offers a better understanding of the error threshold and provides further insight into the plausibility of an ancient RNA world.
Introduction
Ever since the insight of Manfred Eigen [1], researchers have been puzzled by the question how the adverse effect of high mutation rate on the selectively maintainable genome size could be alleviated. The classical, sequence-based error threshold looks like this: imagine a population of wild-type (also called master in this context) and mutant templates of uniform length replicating with a finite accuracy. We further assume that wild-type sequences have high fitness and all the mutant copies have (identical) low fitness. This is obviously a simple fitness landscape. Whereas Eigen's [1] formalism can handle arbitrary fitness landscapes, the derivation of the error threshold is much more straightforward for this simple case. If we further adopt the simplification of no back mutations then a very simple result follows [2] for the critical error rate, 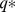 :
:
| (1) |
where 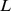 is the length of the sequence and s is the selective superiority of the wild-type sequence. An error rate of 1%, which is already quite an optimistic assumption, allows a sequence not longer than 100 nucleotides to be maintained. Four decades ago this problem looked rather paralyzing: what could a peptide enzymatically do that consisted of a mere 33 amino acids? And even if short peptides could be sufficiently enzymatic, does one gene make a genome?
is the length of the sequence and s is the selective superiority of the wild-type sequence. An error rate of 1%, which is already quite an optimistic assumption, allows a sequence not longer than 100 nucleotides to be maintained. Four decades ago this problem looked rather paralyzing: what could a peptide enzymatically do that consisted of a mere 33 amino acids? And even if short peptides could be sufficiently enzymatic, does one gene make a genome?
In an RNA world [3]–[8], in which RNAs act both as information storage molecules and enzymes, things are likely to have been different. There are ample examples of ribozymes that are less than a 100 nucleotides long [4], [9] (see also Table S1). Actually, the smallest ribozyme is 5 nucleotides long [10]. On the other hand, while a ribozyme can be less than 100 nucleotides long, a single gene still does not make a genome. However, recent investigations have somewhat alleviated the error threshold problem. First, it seems that intragenomic recombination may have shifted the threshold by about 30% [11]. Second, the processivity of replication (i.e. the constraint that during enzymatic template replication nucleotides have to be inserted one by one into the growing copy, and this must happen repeatedly) could have worked against erroneous insertions that slowed down replication: erroneous copies would have thus suffered from a built-in fitness disadvantage [12]. Although this effect was shown to be considerably smaller for RNA than DNA, nevertheless it may also have alleviated the error threshold by about one-third. Third, as we have shown by the analysis of two existing ribozymes (the Neurospora VS [13] and the hairpin ribozyme [14]), the fact that the maintenance of structure is more important for function than that of sequence significantly shifts the error threshold to longer sequences (the genotypic and phenotypic error thresholds are 0.033 versus 0.053 and 0.042 versus 0.144 for the two ribozymes, respectively), in support of the investigations of Takeuchi et al. [15] and Reidys et al. [16]. They proposed that neutral mutations, by keeping the same phenotype, should modify the error threshold:
| (2) |
where the critical parameter 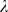 is the degree of neutrality, i.e. the fraction of neutral mutants among the mutants one step away from the master phenotype (the formula is from [15]).
is the degree of neutrality, i.e. the fraction of neutral mutants among the mutants one step away from the master phenotype (the formula is from [15]).
This phenotypic error threshold suggested two important considerations: (1) known ribozymes by the virtue of their small sizes could be replicated by replicases whose accuracy would not have surpassed those of experimentally produced, available polymerase ribozymes (working with error rates in the range 0.04–0.01 per digit per replication [17], [18]), and (2) a replicase working at an error rate one magnitude lower than the currently known polymerase ribozymes could have replicated a small genome of a complete ribo-organims [19], [20].
In this paper, we broaden the investigation of the error threshold into important directions. The questions are:
(1) What structural characteristic of RNAs determines the position of the phenotypic error threshold? More specifically, can the degree of neutrality (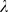 ) be employed to estimate the error threshold as proposed in [15], [16]. Please note, that the formula in Eq. 2 was derived by assuming that the effect of mutations are independent, and thus if there is two mutations that are independently neutral, then a sequence having both of them together will still be neutral. This is not necessary true. Furthermore the degree of neutrality is assumed to be the same for every sequences of the master type. We know that there places of different degree of neutrality along neutral paths (series of sequences having the same phenotype) [21]. Moreover, note that this formula is obtained at zero concentration of the master phenotype, which condition cannot occur when there is back mutation, especially in case of short sequences; it therefore gives an overestimate of the error threshold. In our analysis we start from Eigen's quasispecies model [1] and based on fitness landscapes of folded RNA we analytically calculate the error threshold, and correlate it with structural characteristic, thereby checking Eq. 2.
) be employed to estimate the error threshold as proposed in [15], [16]. Please note, that the formula in Eq. 2 was derived by assuming that the effect of mutations are independent, and thus if there is two mutations that are independently neutral, then a sequence having both of them together will still be neutral. This is not necessary true. Furthermore the degree of neutrality is assumed to be the same for every sequences of the master type. We know that there places of different degree of neutrality along neutral paths (series of sequences having the same phenotype) [21]. Moreover, note that this formula is obtained at zero concentration of the master phenotype, which condition cannot occur when there is back mutation, especially in case of short sequences; it therefore gives an overestimate of the error threshold. In our analysis we start from Eigen's quasispecies model [1] and based on fitness landscapes of folded RNA we analytically calculate the error threshold, and correlate it with structural characteristic, thereby checking Eq. 2.
(2) How general is our previous finding [19] that even low-accuracy replicases could replicate the known ribozymes if only the former were processive enough (i.e. if they could replicate adequately long templates irrespective of the accuracy problem)? Note that the best experimentally verified polymerase ribozyme, while being 198 nt long, can copy sequences up to 95 nt [17] or can copy a very specific template up to 206 nt [22]. If Eq. 2 can be used to estimate the error threshold, then we can make a rough estimate for known ribozyme sequences from the literature, and strengthen (or disprove) our previous claim.
We consider the above raised questions in turn. Finally, we look at the world of putative ribo-organisms in the light of our findings.
Results
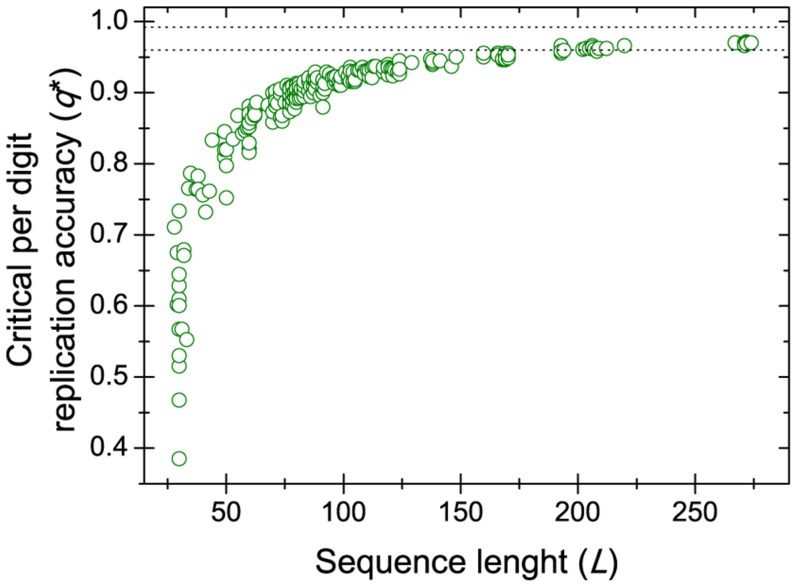
The position of the error threshold for an arbitrary fitness landscape and in the presence of back mutations is a matter of definition in the quasispecies model of Eigen [1], [23], [24]. We have calculated the error threshold for binary (GC) sequences (and the phenotypic error threshold for associated secondary structures) up to length 16. Sequences comprising of only GC nucleotides have similar structural diversity as those composed of all four bases (see below), and thus our results are representative for them as well. Note that even at this length, sequence space is vast (there are 216 = 65536 possible sequences) and exhaustive calculations for longer sequences or sequences with four bases are technically not feasible at the moment. Since the sequences are relatively short in this exhaustive analysis, the error threshold is not as sharp as for longer ones [25], and other types of diagnostics (such as the avoided crossing of the first and second largest eigenvalues [26]) do not work either, we define the error threshold as the error rate where the total concentration of master templates equals that of the non-master.
We employ a simple fitness landscape in which sequences belonging to the same secondary structure class (SSC) defined as the set of sequences of identical length sharing the same secondary structure, have high fitness (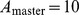 ) and all other sequences have base fitness (
) and all other sequences have base fitness (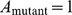 ). The selective superiority is thus
). The selective superiority is thus 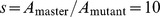 . The minimum free energy structures of the sequences are obtained with the ViennaRNA Package ver. 1.8 [27]. For a given SSC, we set the so called value matrix (cf. Eq. 6) of the system (cf. Eq. 5), which contains the replication and degradation rate constants of the sequences, according to the secondary structure corresponding to the SSC. By computing the leading eigenvector at a given per digit replication accuracy q, we get the equilibrium densities of master and mutant sequences. The value of q at which the densities of master and mutant sequences equal defines our error threshold. (Note that in case of L = 16, the value matrix has 232≈4.3•109 entries; memory consumption and computation time for longer sequences is enormous). The error threshold for major SSCs (SSCs covering at least 0.1% of the sequence space) is calculated.
. The minimum free energy structures of the sequences are obtained with the ViennaRNA Package ver. 1.8 [27]. For a given SSC, we set the so called value matrix (cf. Eq. 6) of the system (cf. Eq. 5), which contains the replication and degradation rate constants of the sequences, according to the secondary structure corresponding to the SSC. By computing the leading eigenvector at a given per digit replication accuracy q, we get the equilibrium densities of master and mutant sequences. The value of q at which the densities of master and mutant sequences equal defines our error threshold. (Note that in case of L = 16, the value matrix has 232≈4.3•109 entries; memory consumption and computation time for longer sequences is enormous). The error threshold for major SSCs (SSCs covering at least 0.1% of the sequence space) is calculated.
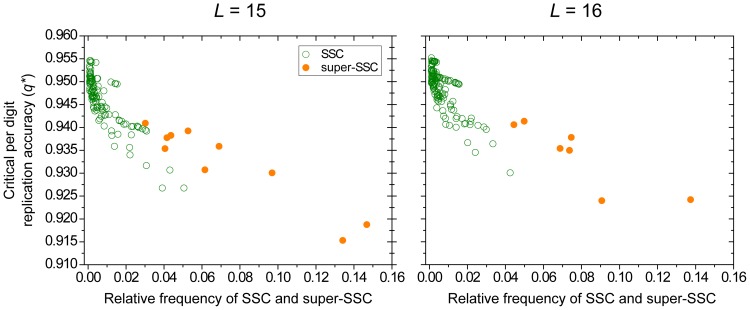
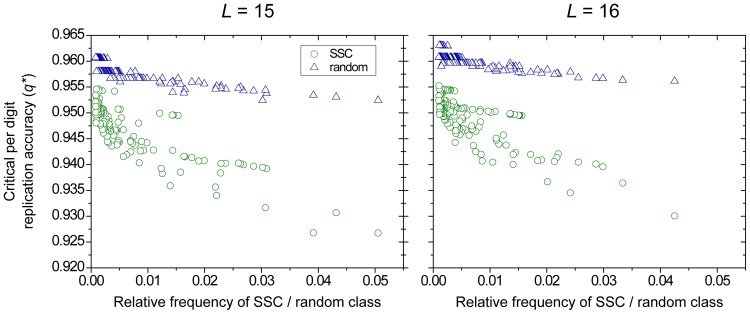
We find that the error threshold of sequences whose structures belong to the same SSC scales inversely with the relative frequency of the SSC genotypes in sequence space (Fig. 1): more common secondary structures are more robust. SSCs consisting of more sequences have a lower critical per digit replication accuracy, hence a more permissive error threshold. This can be understood as a higher number of members translate to a larger neutral network in the sequence space [28]. However, it is not just the mere number of sequences belonging to the class which makes them more robust against errors: Fig. 2 clearly shows that sets of random sequences, even if they have the same size as a SSC, suffer from a remarkably stricter error threshold.
Figure 1. Error thresholds of secondary structure classes (SSCs).
The graphs depict the critical per digit replication accuracies (error thresholds) as a function of the frequency of sequences belonging to an SSC among all possible structures of  (left) and
(left) and 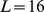 (right). Open circles represent individual SSCs, solid circles represent super-SSCs (SSSC) that merge structures that only differ in the flanking single-stranded regions. Only SSCs are included that cover at least 0.1% of the total sequence space.
(right). Open circles represent individual SSCs, solid circles represent super-SSCs (SSSC) that merge structures that only differ in the flanking single-stranded regions. Only SSCs are included that cover at least 0.1% of the total sequence space.
Figure 2. Error threshold for random sequences.
The green circles represent SSCs based on secondary structures (as in Fig. 1), blue triangles represent the error threshold of classes of random sequences of the same size as the corresponding SSC. Results are for  (left) and
(left) and 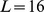 (right).
(right).
A way to extend the investigation of robustness towards more frequent structures is to merge structurally similar SSCs forming a super-SSC. Super-SSC is defined as structures that only differ in the number of leading and trailing single stranded nucleotides (a complete list of super-SSC is found in Table S3).With super-SSCs, the number of sequences belonging to a class can be increased while the main feature of the secondary structure (i.e. the lengths of stem and loop but not their positions in the chain) still remains the same. The above finding still holds for super-SSCs (see Fig. 1, red dots), with super-SSCs having a higher error threshold than any of the error thresholds of their SSCs. Thus if only the major structural features are selected for, the error threshold is even more permissive.
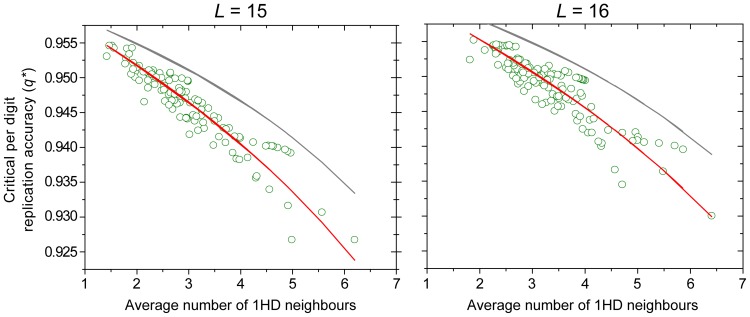
Next, we show that the phenotypic error threshold can be estimated by calculating the fraction of neutral 1-mutant neighbours. (It was previously hinted that it might be sufficient to consider the neutral mutants being just one mutation step away from the master [29]). We have found that for short sequences, the error threshold scales almost linearly with the average number of 1-mutant neighbours in the SSC (Fig. 3), which supports the insight provided by the Takeuchi-Hogeweg formula (Eq. 2). If we introduce the simple assumption that the frequency of back mutations is proportional to the number of 1-step neutral mutants there is a strong correlation between empirical calculations and the corrected Takeuchi-Hogeweg formula for error threshold (cf. Eq. 18 in Methods and the Discussion):
Figure 3. Correlation of the error threshold with average number of 1–Hamming distance neighbours.
Critical per digit replication accuracy of SSCs as a function of the average number of 1–Hamming distance neighbours for sequences in the SSC. Red curves show fit of Eq. 3 to the data points, while the dark gray curve show fit to Eq. 3 with no back-mutations (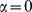 ). Results are for
). Results are for  (left) and
(left) and 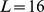 (right). The average number of 1HD neighbours can be transformed to
(right). The average number of 1HD neighbours can be transformed to 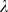 by dividing it by the length of the sequence.
by dividing it by the length of the sequence.
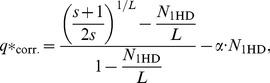 |
(3) |
where s is the selective superiority of the focal phenotype, N 1HD is the number of neutral 1-Hamming distance neighbours and α is the proportionality factor of back mutation. This correction includes the fifty-fifty definition of the error threshold given above and a heuristic account of the effect of back mutations.
We conclude thus that there is an ordering of robustness for two (or more) sequences of identical lengths: the one having more neighbours a single mutation step away with the same phenotype tends to have a higher error threshold.
In order to apply the formula (Eq. 2) to calculate the error threshold, we need the length L of the sequence, the frequency 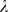 of one-step neutral mutants among all one-step mutants and the selective advantage s of the master phenotype. The length is naturally given, and
of one-step neutral mutants among all one-step mutants and the selective advantage s of the master phenotype. The length is naturally given, and 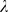 can be calculated exhaustively by folding all possible such mutants and comparing their minimum free energy structures to the secondary structure of the original sequence (this neglects mutations that are harmful even though the secondary structure remains unchanged) as
can be calculated exhaustively by folding all possible such mutants and comparing their minimum free energy structures to the secondary structure of the original sequence (this neglects mutations that are harmful even though the secondary structure remains unchanged) as 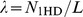 (there are
(there are  such mutant sequences for sequences comprising of only two bases, while there are
such mutant sequences for sequences comprising of only two bases, while there are  such sequences if all four bases are considered) (see Methods for the detailed explanation of the determination of
such sequences if all four bases are considered) (see Methods for the detailed explanation of the determination of 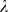 ). For the selective advantage, we apply our previous estimate of
). For the selective advantage, we apply our previous estimate of 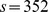 obtained for two fitness landscapes sampled more exhaustively [19].
obtained for two fitness landscapes sampled more exhaustively [19].
Now we turn to the case of real ribozymes and aptamers from the Aptamer Database [30] and from the review of Chen and coworkers [9], providing 305 sequences altogether [31]–[113] (Table S1). This set of sequences represents a considerable fraction of all known aptamers and ribozymes whose functions have prebiotic significance. The ribozymes in particular were selected on the basis of their metabolic importance which suggests their prebiotic significance. It turns out that all of these ribozymes and aptamers have lower critical copying fidelity than the 99% fidelity of the most recent polymerase [17] and most have a critical copying fidelity lower than the average 96.5% fidelity reported for the first putative polymerase [18] (Fig. 4). Thus moderately sized, metabolically important ribozymes can be replicated despite rather low fidelities (high error rates).
Figure 4. Error threshold of real ribozymes and aptamers.
Critical per digit replication accuracy required to replicate real ribozymes and aptamers, calculates using Eq. (2). Each point represents a ribozyme or an aptamer (see Table S1). The two dotted lines mark the zone of replication accuracy of putative RNA-dependent RNA polymerases (0.96 <q <0.99).
Another appreciation of the calculated error thresholds is possible as follows. For every length of aptamers or ribozymes in Table S1, we have folded 1000 randomly chosen RNA sequences of the given length. Of course, this is a small sample, but with good chance we mainly obtain structures that are common in phenotype space [114]. Enzymes are likely to belong to one of these common structures [115], [116]. We have collected λ for all of the 1000 sequences which tells us how the degree of neutrality ( ) of aptamers/ribozymes relates to that of the common structure. Real ribozymes (similarly to SSCs measured above) have rather low degree of neutrality (
) of aptamers/ribozymes relates to that of the common structure. Real ribozymes (similarly to SSCs measured above) have rather low degree of neutrality ( ) because these molecules have been produced by artificial directional selection [117], [118]. Such a decrease in robustness was shown. However, only 48.2% of the considered 305 real sequences (ribozymes and aptamers) have lower
) because these molecules have been produced by artificial directional selection [117], [118]. Such a decrease in robustness was shown. However, only 48.2% of the considered 305 real sequences (ribozymes and aptamers) have lower 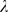 than the median for the random sequences. And 9.1% of the real sequences fall into the upmost decile, i.e. they have a higher
than the median for the random sequences. And 9.1% of the real sequences fall into the upmost decile, i.e. they have a higher 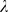 than 90% of random sequences; and 2.2% of the real sequences have higher
than 90% of random sequences; and 2.2% of the real sequences have higher 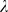 than 95% of the random sequences. All in all the distribution of neutralities is not different from the distribution obtained for the random sequences (see Methods). This is remarkable considering the fact that these ribozymes had been subject to intense directional selection for the required functionality. Although robustness and evolvability are not necessarily in conflict [119], [120], it is legitimate to ask whether stabilizing selection could increase the robustness of these populations further, as demonstrated in the theory of neutral networks [120]. We have thus exerted stabilizing selection on different molecules that already had a rather high
than 95% of the random sequences. All in all the distribution of neutralities is not different from the distribution obtained for the random sequences (see Methods). This is remarkable considering the fact that these ribozymes had been subject to intense directional selection for the required functionality. Although robustness and evolvability are not necessarily in conflict [119], [120], it is legitimate to ask whether stabilizing selection could increase the robustness of these populations further, as demonstrated in the theory of neutral networks [120]. We have thus exerted stabilizing selection on different molecules that already had a rather high 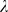 with population size 500 through 5000 generations (the only constraint was to maintain the phenotype). We show the highest degree of neutrality (
with population size 500 through 5000 generations (the only constraint was to maintain the phenotype). We show the highest degree of neutrality (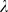 ) for structure-preserving variants (Fig. 5). It is apparent that stabilizing selection can guide robustness to the top 25% or even 5% of the distribution obtained for random sequences. Thus, we can expect that ribozymes in primordial ribo-organisms were even more error-resistant than ribozymes evolved in vitro, as they were subject to many generations of stabilizing selection.
) for structure-preserving variants (Fig. 5). It is apparent that stabilizing selection can guide robustness to the top 25% or even 5% of the distribution obtained for random sequences. Thus, we can expect that ribozymes in primordial ribo-organisms were even more error-resistant than ribozymes evolved in vitro, as they were subject to many generations of stabilizing selection.
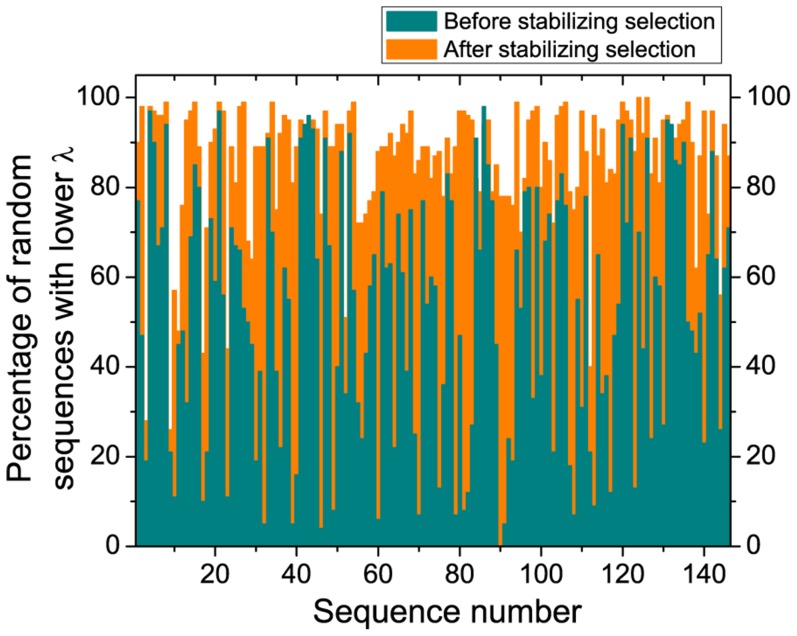
Figure 5. Stabilizing selection increases robustness of sequences.
The percentage of the random sequences having lower fraction of 1-step neutral mutants among all 1-step mutants (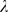 ) than the original sequence (green bars) and the best sequence after 5000 generations of stabilizing selection (orange bars). Sequences are ordered according to their length. Exact
) than the original sequence (green bars) and the best sequence after 5000 generations of stabilizing selection (orange bars). Sequences are ordered according to their length. Exact 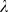 are given in Table S1.
are given in Table S1.
Discussion
We have found that the number of 1-step neutral mutants, for short sequences, is an excellent predictor of the error threshold (Fig. 2). Other characteristics of structure (see for example in [121]) are not as highly correlated with the error threshold. Maintenance of RNA secondary structure is a good predictor of maintenance of enzymatic activity [122], but especially around the active site the actual nucleotides presents are also important. In this investigation we have not considered critical sites in our fitness landscape, which would lower the degree of neutrality of sequences. Considering critical sites would most probably not affect the correlation of error threshold with the degree of neutrality.
The possibility of estimating the error threshold by available and easily computable characteristic of RNA sequences allows us to assess the replicability of aptamers and ribozymes. We have shown that functional phenotypes are mutationally robust above chance level and that, in effect, most known ribozymes could be replicated by a replicase working at the accuracy of the currently best RNA-dependent RNA polymerase ribozyme [17] (Fig. 4). Stabilizing selection, after the acquisition of function, can guide these molecular replicators to regions of sequence space which further increase robustness (Fig. 5).
It is important to discuss how our approach relates to the approach of Takeuchi et al.
[15]. Their formula Eq. (2) was derived from heuristic considerations. We have explicitly numerically computed the error threshold for lengths up to 16 using the criterion of master phenoype to all others being 1∶1 in equilibrium concentrations. Note that since we calculate explicitly, back mutations naturally are accounted for and are thus are not neglected. One of the results of the present paper is that the “top-down” formula of Takeuchi et al. is in qualitative agreement with our bottom-up quantitative results. The relation between their critical parameter and ours is 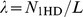 . Using our 50% criterion for the error threshold we obtain the modified form of the Takeuchi-Hogeweg error threshold (Eq. (2)):
. Using our 50% criterion for the error threshold we obtain the modified form of the Takeuchi-Hogeweg error threshold (Eq. (2)):
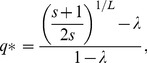 |
(4) |
which does not agree quantitatively with our data (Fig. 3). This is why we have introduced the correction factor α accounting for back mutations in Eq. (3) under the assumption that back mutations from multiple deleterious mutants can be ignored. Note that the formula in Eq. (3) is non-linear but gives good fit for short sequences. With longer sequences the linear relationship between the error threshold and 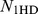 slowly deteriorates, and as shown in Fig. 3, there is increasing scatter around the nonlinear curve as well.
slowly deteriorates, and as shown in Fig. 3, there is increasing scatter around the nonlinear curve as well.
It is good news that individually all known ribozymes (genes) could be replicated in a realistic RNA world, but we must return to the important question as to how small genomes could have come into being. If we adopt the view that unlinked, naked genes preceded protocells and chromosomes [123] we should be happy with the current finding. There are mechanisms of dynamical coexistence of naked, unlinked replicators spreading on surfaces [124], [125]. In such a case, each sequence is competing with its own mutated copies (mutants can occasionally evolve into something new and useful [126]). We concur that such surface-bound dynamics was a stepping stone to “serious” forms of compartmentation, such as protocells [127]. Protocells can harbour a fair number of different, competing genes [128], but only if the error rate is low enough. It is plausible that error rates did evolve during the pre-cellular era of surface dynamics: more efficient (more accurate and faster) model replicases have been shown to spread on surfaces by kin selection [129]. We confirm the previous result in [19] that the transition from surface to protocell dynamics required only an order of magnitude increase in replication accuracy!
Methods
Derivation and analytical computation of the error threshold
The computation of the error threshold is based on the original quasispecies model of Eigen [1], [23], [24]:
| (5) |
where xk(t) is density of sequence k at time t; the coefficients 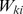 are elements of a value matrix W which contains replication and degradation rate constants (
are elements of a value matrix W which contains replication and degradation rate constants (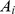 and
and 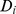 , respectively) and mutation frequencies (
, respectively) and mutation frequencies (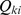 ) (the value matrix is filled according to the fitness landscape employed (see Results)):
) (the value matrix is filled according to the fitness landscape employed (see Results)):
| (6) |
and 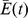 is the mean excess production:
is the mean excess production:
| (7) |
which can be removed by a non-linear transformation [23], [130]–[132] resulting an essentially linear equation. The model assumes that the only source of sequences is the correct or erroneous copies of present sequences; the substrates for replication are always present in sufficient quantity and excess molecules are washed out by a flux that keeps the total concentration constant.
As independent point mutations are assumed, mutation probability depends only on the Hamming distance of the initial (i) and final (k) binary sequences of length 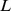 :
:
| (8) |
where 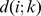 stands for the Hamming distance between the two sequences,
stands for the Hamming distance between the two sequences, 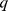 is the (constant) per digit replication accuracy,
is the (constant) per digit replication accuracy, 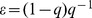 .
.
The dynamics of the system is governed by the leading eigenvalue and the corresponding eigenvector of W. We assume that there is no degradation (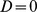 ), which does not affect the eigenvectors. Let
), which does not affect the eigenvectors. Let 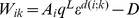 define the value matrix of the system and thus the modified equation without degradation is
define the value matrix of the system and thus the modified equation without degradation is  .
. 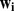 and
and 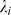 are eigenvectors and eigenvalues of the original matrix:
are eigenvectors and eigenvalues of the original matrix:
| (9) |
Consequently:
| (10) |
thus 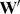 has the same eigenvectors and this type of transformation does not affect the rank of the eigenvalues.
has the same eigenvectors and this type of transformation does not affect the rank of the eigenvalues.
The analytical solution of the system is the following, see e.g. [24], [132]:
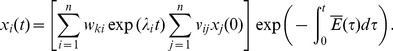 |
(11) |
We are interested in the 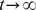 limit only. In this case:
limit only. In this case:
| (12) |
where 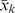 is the equilibrium mutant distribution, the “quasispecies” which consists of mutants distributed around the most efficient variant, called the master sequence.
is the equilibrium mutant distribution, the “quasispecies” which consists of mutants distributed around the most efficient variant, called the master sequence.
Equation (3) can be solved either by integrating this ordinary differential equation numerically e.g. via Runge–Kutta method or computing the leading eigenvalue λ1 and the corresponding right eigenvector (w). We use the latter, simpler method because of its smoother behavior.
To compute the leading eigenvalue and the corresponding right eigenvector we used the Krylov-Schur method implemented in the SLEPc library [133] using the PETSc matrix routines [134].
We have computed the error threshold of a system in the following way: (1) The value matrix of Eq. (5) was filled according to the fitness landscape (high fitness  , base fitness
, base fitness  ), using
), using 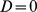 . (2) The leading eigenvector w was computed at two per-digit replication accuracy values:
. (2) The leading eigenvector w was computed at two per-digit replication accuracy values: 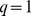 and
and 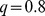 (in our systems, the error threshold always lies in this interval). From w it is easy to compute the total density of the master and mutant sequences. (3) The value of q at which the densities of the master and mutant sequences are the same is the error threshold (by our definition), thus we applied a secant algorithm to find the intersection point of the densities as a function of q (at a relative precision of 10−6). (4) The resulting
(in our systems, the error threshold always lies in this interval). From w it is easy to compute the total density of the master and mutant sequences. (3) The value of q at which the densities of the master and mutant sequences are the same is the error threshold (by our definition), thus we applied a secant algorithm to find the intersection point of the densities as a function of q (at a relative precision of 10−6). (4) The resulting 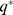 is the error threshold. The computation of an error threshold (with an arbitrary fitness landscape) using this algorithm – with a slight modification of the SLEPc code to reduce memory consumption – took about 12 hours and needed 4 GB of RAM on a 2.6 GHz Intel Xeon CPU.
is the error threshold. The computation of an error threshold (with an arbitrary fitness landscape) using this algorithm – with a slight modification of the SLEPc code to reduce memory consumption – took about 12 hours and needed 4 GB of RAM on a 2.6 GHz Intel Xeon CPU.
Analytical formulation of the phenotypic error threshold
Using the phenotypic dynamics described by Takeuchi et al. [15], the starting point is the following pair of differential equations:
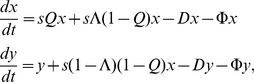 |
(13) |
where x and y denote the focal phenotype and mutants, respectively; Q is the replication accuracy of x; Λ is the fraction of neutral mutants of  ; D is the constant degradation rate;
; D is the constant degradation rate; 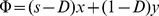 is the excess production; and s is the replication rate of the focal phenotype, while the mutants' replication rates are normalized to 1. We keep the concentration constant, i.e.
is the excess production; and s is the replication rate of the focal phenotype, while the mutants' replication rates are normalized to 1. We keep the concentration constant, i.e. 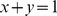 . Computing the steady state solution for
. Computing the steady state solution for 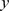 yields:
yields:
| (14) |
where
| (15) |
is the effective replication accuracy. Assuming that the number of neutral substitutions follows the binomial distribution (q denotes the correct per-digit replication probability):
| (16) |
Our criterion for error threshold implies y* = 1/2. Combining these results, the critical per-digit replication accuracy (our error threshold) is
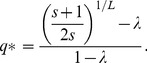 |
(17) |
This calculation ignores back mutations. With the simple assumption that the frequency of back mutations is proportional (by a factor of α) to the number of 1-step mutants (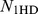 ), we get the following corrected critical per-digit replication accuracy:
), we get the following corrected critical per-digit replication accuracy:
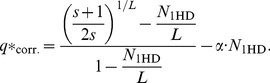 |
(18) |
Structural diversity of GC and GCAU sequences
Due to technical limitations, we have calculated the error threshold using sequences composed only of G and C, i.e. only two letters from the canonical four letter alphabet. Our question was: Would structural diversity, measured as the number of distinct structures and their relative frequencies, differ substantially for two and four letters?
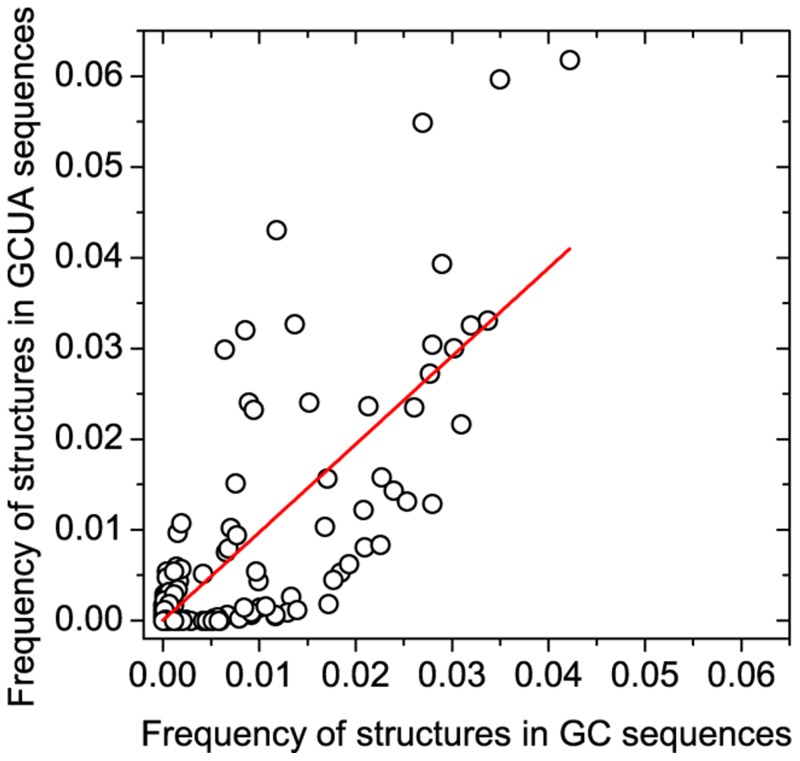
We have enumerated all sequences of length 14 using only GC nucleotides and using all four (GCAU). There are 16,384 unique GC sequences folding into 107 distinct structures (Table S2), whereas there are 268,435,456 unique GCAU sequences folding into 230 distinct structures (Table S2). In the case of the four-letter sequences, the most common structure (72.2%) is the one without any internal base-pair, in the binary sequences this structure has a much lower frequency (4.3%) due to the higher probability of having possible base-pairings in the sequence. If we leave out this structure, the relative frequencies of the remaining structures correlate in the two-base and four-base sequences. Correlation between frequencies is relatively high (0.79) (Fig. 6). A detailed investigation of RNA sequences of various alphabets can be found in [135].
Figure 6. Correlation of structure frequencies of GC (two-letter) and GCAU (four-letter) sequences of length 14.
Calculation of the fraction of neutral 1-step mutants
For each sequence, the minimum free-energy structures of all 1-step mutants (differing only in one position from the original) are obtained. The number of 1-step mutants having the same structure as the original sequence is divided by the number of all possible 1-step mutants (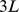 ) is the fraction of neutral one-mutants,
) is the fraction of neutral one-mutants, 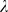 .
.
Populations consisting of 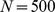 ribozymes were allowed to evolve for
ribozymes were allowed to evolve for 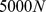 replications. At each replication each nucleotide of a sequence has a
replications. At each replication each nucleotide of a sequence has a 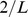 chance to mutate. This error rate is below the error threshold for all considered sequences. Sequences are chosen randomly for replication, with probability proportional to their structural similarity compared to the wild-type sequence. Thus we apply stabilizing selection on the structure of the wild-type sequence. After the
chance to mutate. This error rate is below the error threshold for all considered sequences. Sequences are chosen randomly for replication, with probability proportional to their structural similarity compared to the wild-type sequence. Thus we apply stabilizing selection on the structure of the wild-type sequence. After the 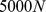 th replication,
th replication, 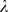 is calculated for each sequence folding to the original structure. The highest value among these is recorded.
is calculated for each sequence folding to the original structure. The highest value among these is recorded.
Statistical analysis
In order to statistically assess how the number of 1HD mutants of real ribozymes and aptamers before and after stabilizing selection relate to the distribution of number of 1HD mutants of random sequences, we calculated the percentile rank of data points in the random ensemble. Rank here means the average percentage ranking of the number of 1HD mutants. In case of multiple matches, average the percentage rankings of all matching scores. Percentiles are then divided into 10 bins of equal size between 0% and 100%. If the bins are equally populated then the distribution of the number of 1HD mutants for the real data is not different from that obtained for random sequences. Similarity of the distribution is assesses by  test. Multiple sequences come from the same study in our dataset, and thus the independency of the data point does not hold. Thus, we only use the sequences that are used in our analysis for further evolution, as we have only picked one from each study of similar length sequences. The distribution of the number of 1 HD mutants is not different from the distribution for random sequences (
test. Multiple sequences come from the same study in our dataset, and thus the independency of the data point does not hold. Thus, we only use the sequences that are used in our analysis for further evolution, as we have only picked one from each study of similar length sequences. The distribution of the number of 1 HD mutants is not different from the distribution for random sequences (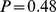 ). (Please note that for the whole set it would be
). (Please note that for the whole set it would be 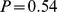 , so the same.) After stabilizing selection is applied the distribution is markedly different from the one obtained for random sequences (
, so the same.) After stabilizing selection is applied the distribution is markedly different from the one obtained for random sequences (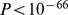 ).
).
Supporting Information
Error threshold of real ribozymes and aptamers. RNA sequences of ribozymes and aptamers from the literature is listed alongside their length, number of 1-neighbour neutral mutants, frequency of nearest-neighbour (one-step) neutral mutants (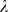 ), the estimated error threshold and the citation for the sequence. Stabilizing selection was applied to selected sequences, and the highest number of 1-neighbour neutral mutants is reported here.
), the estimated error threshold and the citation for the sequence. Stabilizing selection was applied to selected sequences, and the highest number of 1-neighbour neutral mutants is reported here.
(XLSX)
Structural diversity of RNA sequences of length 14 with two letter (GC) and four letter (GCAU) alphabet. Secondary structures in bracket notation are reported with the number of unique sequences folding to this structure. Frequencies of structures among all possible structures of length 14 are reported. The unstructured structure has the highest frequency among the sequences built from four letters. We also report the frequencies of structures if we omit these sequences from the total count.
(XLSX)
Secondary structure classes and Super secondary structure classes of GC sequences of length 16. Secondary structures in bracket notation are reported with the number of unique sequences folding to this structure. The first column show the super secondary structure class (SSSC) without leading and trailing single stranded nucleotides. The second column gives the total number of unique sequences folding into the SSSC. Then in column 3 the individual structures are reported as well as their total unique sequence count (column 4).
(XLSX)
Acknowledgments
We thank Viktor Péter Kovács, who helped us solve problems relating to the computation of the eigenvectors of big matrices.
Data Availability
The authors confirm that all data underlying the findings are fully available without restriction. All relevant data are within the paper and its Supporting Information files.
Funding Statement
Financial support has been provided by the European Research Council under the European Community's Seventh Framework Programme (FP7/2007–2013)/ERC grant agreement no [294332] and the Hungarian National Office for Research and Technology (NAP 2005/KCKHA005). AS and ÁK acknowledge support by the European Union and co-financed by the European Social Fund (grant agreement no. TAMOP 4.2.1/B-09/1/KMR-2010-0003). This work was carried out as part of EU COST action CM1304 “Emergence and Evolution of Complex Chemical Systems”. ÁK gratefully acknowledges a János Bolyai Research Fellowship of the Hungarian Academy of Sciences. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Eigen M (1971) Selforganization of matter and the evolution of biological macromolecules. Naturwissenscaften 10: 465–523. [DOI] [PubMed] [Google Scholar]
- 2. Maynard Smith J (1983) Models of evolution. Proceedings of the Royal Society of London B 219: 315–325. [Google Scholar]
- 3. Bernhardt H (2012) The RNA world hypothesis: the worst theory of the early evolution of life (except for all the others). Biology Direct 7: 23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Joyce GF (2002) The antiquity of RNA-based evolution. Nature 418: 214–220. [DOI] [PubMed] [Google Scholar]
- 5.Maurel M-C, Haenni AL (2005) The RNA world: Hypothesis, facts and experimental results. In: Barbier B, Gargaud M, Martin H, Reisse J, editors. Lectures in Astrobiology: Springer Verlag Ed. pp. 557–581. [Google Scholar]
- 6. Dworkin JP, Lazcano A, Miller SL (2003) The roads to and from the RNA world. Journal of Theoretical Biology 222: 127–134. [DOI] [PubMed] [Google Scholar]
- 7.Cech TR, Atkins JF, Gesteland RF, editors (2005) The RNA World. 3rd edition ed: Cold Spring Harbor Laboratory Press. 768 p. [Google Scholar]
- 8.Yarus M (2011) Life from an RNA World: The Ancestor Within. Harvard, USA: Harvard University Press. [Google Scholar]
- 9. Chen X, Li N, Ellington AD (2007) Ribozyme catalysis of metabolism in the RNA World. Chemistry & Biodiversity 4: 633–655. [DOI] [PubMed] [Google Scholar]
- 10. Chumachenko NV, Novikov Y, Yarus M (2009) Rapid and simple ribozymic aminoacylation using three conserved nucleotides. Journal of American Chemical Society 131: 5257–5263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Santos M, Zintzaras E, Szathmáry E (2004) Recombination in primeval genomes: a step forward but still a long leap from maintaining a sizeable genome. Journal of Molecular Evolution 59: 507–519. [DOI] [PubMed] [Google Scholar]
- 12. Rajamani S, Ichida JK, Antal T, Treco DA, Leu K, et al. (2010) Effect of stalling after mismatches on the error catastrophe in nonenzymatic nucleic acid replication. Journal of the American Chemical Society 132: 5880–5885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Lafontaine DA, Norman DG, Lilley DMJ (2002) The structure and active site of the Varkund satellite ribozyme. Biochemical Society Transactions 30: 1170–1175. [DOI] [PubMed] [Google Scholar]
- 14. Fedor M (2000) Structure and function of the hairpin ribozyme. Journal of Molecular Biology 297: 269–291. [DOI] [PubMed] [Google Scholar]
- 15. Takeuchi N, Poorthuis PH, Hogeweg P (2005) Phenotypic error threshold; additivity and epistasis in RNA evolution. BMC Evolutionary Biology 5: 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Reidys C, Forst CV, Schuster P (2001) Replication and mutation on neutral networks. Bulletin of Mathematical Biology 63: 57–94. [DOI] [PubMed] [Google Scholar]
- 17. Wochner A, Attwater J, Coulson A, Holliger P (2011) Ribozyme-catalyzed transcription of an active ribozyme. Science 332: 209–212. [DOI] [PubMed] [Google Scholar]
- 18. Johnston WK, Unrau PJ, Lawrence MS, Glasen ME, Bartel DP (2001) RNA-catalyzed RNA polymerization: accurate and general RNA-templated primer extension. Science 292: 1319–1325. [DOI] [PubMed] [Google Scholar]
- 19. Kun Á, Mauro S, Szathmáry E (2005) Real ribozymes suggest a relaxed error threshold. Nature Genetics 37: 1008–1011. [DOI] [PubMed] [Google Scholar]
- 20. Flintoft L (2005) A relaxed approach to errors. Nature Reviews Genetics 6: 724–724. [Google Scholar]
- 21. van Nimwegen E, Crutchfield JP, Huynen MA (1999) Neutral evolution of mutational robustness. Proceedings of the National Academy of Sciences of the USA 96: 9716–9720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Attwater J, Wochner A, Holliger P (2013) In-ice evolution of RNA polymerase ribozyme activity. Nature Chemistry 5: 1011–1018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Eigen M, McCaskill JS, Schuster P (1988) Molecular quasi-species. Journal of Physical Chemistry 92.. [Google Scholar]
- 24. Wilke CO, Ronnewinkel C, Martinetz T (2001) Dynamic fitness landscapes in molecular evolution. Physics Reports 349: 395–446. [Google Scholar]
- 25. Swetina J, Schuster P (1982) A model for polynucleotide replication. Biophysical Chemistry 46: 187–203. [DOI] [PubMed] [Google Scholar]
- 26. Nowak M, Schuster P (1989) Error thresholds of replication in finite populations mutation frequencies and the onset of muller's ratchet. Journal of Theoretical Biology 137: 375–395. [DOI] [PubMed] [Google Scholar]
- 27. Hofacker IL, Fontana W, Stadler PF, Bonhoeffer S, Tacker M, et al. (1994) Fast folding and comparison of RNA secondary structures. Monatchefte für Chemie 125: 167–188. [Google Scholar]
- 28. Grüner W, Giegerich R, Strothmann D, Reidys C, Weber J, et al. (1996) Analysis of RNA sequence structure maps by exhaustive enumeration II. Structures of neutral networks and shape space covering. Monatshefte für Chemie/Chemical Monthly 127: 375–389. [Google Scholar]
- 29. Schuster P, Stadler PF (1999) Nature and evolution of early replicons. In: Origin and Evolution of Viruses Domingo E, Webster RG, Holland J, editors. New York: Academic Press; pp. 1–24. [Google Scholar]
- 30. Lee JF, Hesselberth JR, Meyers LA, Ellington AD (2004) Aptamer Database. Nucleic Acid Research 32: D95–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Beaudry AA, Joyce GF (1992) Directed evolution of an RNA enzyme. Science 257: 635–641. [DOI] [PubMed] [Google Scholar]
- 32. Bell SD, Denu JM, Dixon JE, Ellington AD (1998) RNA molecules that bind to and inhibit the active site of a tyrosine phosphatase. Journal of Biological Chemistry 273: 14309–14314. [DOI] [PubMed] [Google Scholar]
- 33. Berens C, Thain A, Schroeder R (2001) A tetracycline-binding RNA aptamer. Bioorganic & Medicinal Chemistry 9: 2549–2556. [DOI] [PubMed] [Google Scholar]
- 34. Bridonneau P, Chang Y-F, O'Connell D, Gill SC, Snyder DW, et al. (1998) High-affinity aptamers selectively inhibit human nonpancreatic secretory phospholipase A2 (hnps-PLA2). Journal of Medicinal Chemistry 41: 778–786. [DOI] [PubMed] [Google Scholar]
- 35. Brockstedt U, Uzarowska A, Montpetit A, Pfau W, Labuda D (2004) In vitro evolution of RNA aptamers recognizing carcinogenic aromatic amines. Biochemical and Biophysical Research Communications 313: 1004–1008. [DOI] [PubMed] [Google Scholar]
- 36. Cerchia L, Ducongé F, Pestourie C, Boulay J, Aissouni Y, et al. (2005) Neutralizing aptamers from whole-cell SELEX inhibit the RET receptor tyrosine kinase. PLOS Biol 3: e123. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 37. Chen C-hB, Chernis GA, Hoang VQ, Landgraf R (2003) Inhibition of heregulin signaling by an aptamer that preferentially binds to the oligomeric form of human epidermal growth factor receptor-3. Proceedings of the National Academy of Sciences 100: 9226–9231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Coleman TM, Huang F (2002) RNA-catalyzed thioester synthesis. Chemistry & Biology 9: 1227–1236. [DOI] [PubMed] [Google Scholar]
- 39. Conn MM, Prudent JR, Schultz PG (1996) Porphyrin metalation catalyzed by a small RNA molecule. Journal of the American Chemical Society 118: 7012–7013. [Google Scholar]
- 40. Conrad R, Keranen LM, Ellington AD, Newton AC (1994) Isozyme-specific inhibition of protein kinase C by RNA aptamers. Journal of Biological Chemistry 269: 32051–32054. [PubMed] [Google Scholar]
- 41. Conrad R, Ellington AD (1996) Detecting immobilized protein kinase C isozymes with RNA aptamers. Analytical Biochemistry 242: 261–265. [DOI] [PubMed] [Google Scholar]
- 42. Cox JC, Rudolph P, Ellington AD (1998) Automated RNA selection. Biotechnology Progress 14: 845–850. [DOI] [PubMed] [Google Scholar]
- 43. Cox JC, Ellington AD (2001) Automated selection of anti-Protein aptamers. Bioorganic & Medicinal Chemistry 9: 2525–2531. [DOI] [PubMed] [Google Scholar]
- 44. Daniels DA, Chen H, Hicke BJ, Swiderek KM, Gold L (2003) A tenascin-C aptamer identified by tumor cell SELEX: Systematic evolution of ligands by exponential enrichment. Proceedings of the National Academy of Sciences 100: 15416–15421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Eulberg D, Buchner K, Maasch C, Klussmann S (2005) Development of an automated in vitro selection protocol to obtain RNA-based aptamers: identification of a biostable substance P antagonist. Nucleic Acids Research 33: e45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Fukuda K, Vishnuvardhan D, Sekiya S, Hwang J, Kakiuchi N, et al. (2000) Isolation and characterization of RNA aptamers specific for the hepatitis C virus nonstructural protein 3 protease. European Journal of Biochemistry 267: 3685–3694. [DOI] [PubMed] [Google Scholar]
- 47. Fusz S, Eisenführ A, Srivatsan SG, Heckel A, Famulok M (2005) A ribozyme for the aldol reaction. Chemistry & Biology 12: 941–950. [DOI] [PubMed] [Google Scholar]
- 48. Gal SW, Amontov S, Urvil PT, Vishnuvardhan D, Nishikawa F, et al. (1998) Selection of a RNA aptamer that binds to human activated protein C and inhibits its protease function. European Journal of Biochemistry 252: 553–562. [DOI] [PubMed] [Google Scholar]
- 49. Gebhardt K, Shokraei A, Babaie E, Lindqvist BH (2000) RNA aptamers to S-adenosylhomocysteine: Kinetic properties, divalent cation dependency, and comparison with anti-S-adenosylhomocysteine antibody. Biochemistry 39: 7255–7265. [DOI] [PubMed] [Google Scholar]
- 50. Geiger A, Burgstaller P, von der Eltz H, Roeder A, Famulok M (1996) RNA aptamers that bind l-arginine with sub-micromolar dissociation constants and high enantioselectivity. Nucleic Acids Research 24: 1029–1036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Gening LV, Klincheva SA, Reshetnjak A, Grollman AP, Miller H (2006) RNA aptamers selected against DNA polymerase β inhibit the polymerase activities of DNA polymerases β and κ. Nucleic Acids Research 34: 2579–2586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Hager AJ, Szostak JW (1997) Isolation of novel ribozymes that ligate AMP-activated RNA substrates. Chemistry & Biology 4: 607–617. [DOI] [PubMed] [Google Scholar]
- 53. Haller AA, Sarnow P (1997) In vitro selection of a 7-methyl-guanosine binding RNA that inhibits translation of capped mRNA molecules. Proceedings of the National Academy of Sciences 94: 8521–8526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Hamm J, Huber J, Lührmann R (1997) Anti-idiotype RNA selected with an anti-nuclear export signal antibody is actively transported in oocytes and inhibits Rev- and cap-dependent RNA export. Proceedings of the National Academy of Sciences 94: 12839–12844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Hartmann R, Nørby PL, Martensen PM, Jørgensen P, James MC, et al. (1998) Activation of 2′-5′ oligoadenylate synthetase by single-stranded and double-stranded RNA aptamers. Journal of Biological Chemistry 273: 3236–3246. [DOI] [PubMed] [Google Scholar]
- 56. Hesselberth JR, Miller D, Robertus J, Ellington AD (2000) In vitro selection of RNA molecules that Inhibit the activity of ricin A-chain. Journal of Biological Chemistry 275: 4937–4942. [DOI] [PubMed] [Google Scholar]
- 57. Hirao I, Harada Y, Nojima T, Osawa Y, Masaki H, et al. (2004) In vitro selection of RNA aptamers that bind to colicin E3 and structurally resemble the decoding site of 16S ribosomal RNA. Biochemistry 43: 3214–3221. [DOI] [PubMed] [Google Scholar]
- 58. Hirao I, Spingola M, Peabody D, Ellington A (1998) The limits of specificity: An experimental analysis with RNA aptamers to MS2 coat protein variants. Molecular Diversity 4: 75–89. [DOI] [PubMed] [Google Scholar]
- 59. Hornung V, Hofmann H-P, Sprinzl M (1998) In vitro selected RNA molecules that bind to elongation factor Tu. Biochemistry 37: 7260–7267. [DOI] [PubMed] [Google Scholar]
- 60. Huang F, Bugg CW, Yarus M (2000) RNA-catalyzed CoA, NAD, and FAD synthesis from phosphopantetheine, NMN, and FMN. Biochemistry 39: 15548–15555. [DOI] [PubMed] [Google Scholar]
- 61. Huang F, Yarus M (1997) 5′-RNA self-capping from guanosine diphosphate. Biochemistry 36: 6557–6563. [DOI] [PubMed] [Google Scholar]
- 62. Li N, Huang F (2005) Ribozyme-catalyzed aminoacylation from CoA thioesters. Biochemistry 44: 4582–4590. [DOI] [PubMed] [Google Scholar]
- 63. Hwang B, Lee S-W (2002) Improvement of RNA aptamer activity against myasthenic autoantibodies by extended sequence selection. Biochemical and Biophysical Research Communications 290: 656–662. [DOI] [PubMed] [Google Scholar]
- 64. Illangasekare M, Yarus M (1999) A tiny RNA that catalyzes both aminoacyl-tRNA and peptidyl-RNA synthesis. RNA 5: 1482–1489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Illangasekare M, Yarus M (1999) Specific, rapid synthesis of Phe-RNA by RNA. Proceedings of the National Academy of Sciences 96: 5470–5475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Jadhav VR, Yarus M (2002) Acyl-CoAs from coenzyme ribozymes. Biochemistry 41: 723–729. [DOI] [PubMed] [Google Scholar]
- 67. Jayasena VK, Gold L (1997) In vitro selection of self-cleaving RNAs with a low pH optimum. Proceedings of the National Academy of Sciences 94: 10612–10617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Jenne A, Famulok M (1998) A novel ribozyme with ester transferase activity. Chemistry & Biology 5: 23–34. [DOI] [PubMed] [Google Scholar]
- 69. Jeong S, Eom T-Y, Kim S-J, Lee S-W, Yu J (2001) In vitro selection of the RNA aptamer against the sialyl Lewis X and its inhibition of the cell adhesion. Biochemical and Biophysical Research Communications 281: 237–243. [DOI] [PubMed] [Google Scholar]
- 70. Jones LA, Clancy LE, Rawlinson WD, White PA (2006) High–affinity aptamers to subtype 3a hepatitis C virus polymerase display genotypic specificity. Antimicrob Agents Chemother 50: 3019–3027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Katahira M, Kobayashi S-i, Matsugami A, Ouhashi K, Uesugi S, et al. (1999) Structural study of an RNA aptamer for a Tat protein complexed with ligands. Nucleic Acids Symposium Series 42: 269–270. [DOI] [PubMed] [Google Scholar]
- 72. Khvorova A, Kwak Y-G, Tamkun M, Majerfeld I, Yarus M (1999) RNAs that bind and change the permeability of phospholipid membranes. Proceedings of the National Academy of Sciences 96: 10649–10654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Kikuchi K, Umehara T, Fukuda K, Kuno A, Hasegawa T, et al. (2005) A hepatitis C virus (HCV) internal ribosome entry site (IRES) domain III-IV-targeted aptamer inhibits translation by binding to an apical loop of domain IIId. Nucleic Acids Res 33: 683–692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Ogawa A, Tomita N, Kikuchi N, Sando S, Aoyama Y (2004) Aptamer selection for the inhibition of cell adhesion with fibronectin as target. Bioorganic & Medicinal Chemistry Letters 14: 4001–4004. [DOI] [PubMed] [Google Scholar]
- 75. Kim SJ, Kim MY, Lee JH, You JC, Jeong S (2002) Selection and stabilization of the RNA aptamers against the Human Immunodeficiency Virus Type-1 nucleocapsid protein. Biochemical and Biophysical Research Communications 291: 925–931. [DOI] [PubMed] [Google Scholar]
- 76. Kimoto M, Shirouzu M, Mizutani S, Koide H, Kaziro Y, et al. (2002) Anti-(Raf-1) RNA aptamers that inhibit Ras-induced Raf-1 activation. European Journal of Biochemistry 269: 697–704. [DOI] [PubMed] [Google Scholar]
- 77. Koizumi M, Breaker RR (2000) Molecular recognition of cAMP by an RNA aptamer. Biochemistry 39: 8983–8992. [DOI] [PubMed] [Google Scholar]
- 78. Kumar PKR, Machida K, Urvil PT, Kakiuchi N, Vishnuvardhan D, et al. (1997) Isolation of RNA aptamers specific to the NS3 protein of hepatitis C virus from a pool of completely random RNA. Virology 237: 270–282. [DOI] [PubMed] [Google Scholar]
- 79. Kumar RK, Yarus M (2001) RNA-catalyzed amino acid activation. Biochemistry 40: 6998–7004. [DOI] [PubMed] [Google Scholar]
- 80. Lee SK, Park MW, Yang EG, Yu J, Jeong S (2005) An RNA aptamer that binds to the β-catenin interaction domain of TCF-1 protein. Biochemical and Biophysical Research Communications 327: 294–299. [DOI] [PubMed] [Google Scholar]
- 81. Legiewicz M, Yarus M (2005) A more complex isoleucine aptamer with a cognate triplet. Journal of Biological Chemistry 280: 19815–19822. [DOI] [PubMed] [Google Scholar]
- 82. Lorger M, Engstler M, Homann M, Göringer HU (2003) Targeting the variable surface of African trypanosomes with variant surface glycoprotein-specific, serum-stable RNA pptamers. Eukaryotic Cell 2: 84–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83. Lupold SE, Hicke BJ, Lin Y, Coffey DS (2002) Identification and characterization of nuclease-stabilized RNA molecules that bind human prostate cancer cells via the prostate-specific membrane antigen. Cancer Research 62: 4029–4033. [PubMed] [Google Scholar]
- 84. Mannironi C, Scerch C, Fruscoloni P, Tocchini-Valentini GP (2000) Molecular recognition of amino acids by RNA aptamers: The evolution into an L-tyrosine binder of a dopamine-binding RNA motif. RNA 6: 520–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Meli M, Vergne J, Maurel M-C (2003) In vitro selection of adenine-dependent hairpin ribozymes. Journal of Biological Chemistry 278: 9835–9842. [DOI] [PubMed] [Google Scholar]
- 86. Missailidis S, Thomaidou D, Borbas KE, Price MR (2005) Selection of aptamers with high affinity and high specificity against C595, an anti-MUC1 IgG3 monoclonal antibody, for antibody targeting. Journal of Immunological Methods 296: 45–62. [DOI] [PubMed] [Google Scholar]
- 87. Miyakawa S, Oguro A, Ohtsu T, Imataka H, Sonenberg N, et al. (2006) RNA aptamers to mammalian initiation factor 4G inhibit cap-dependent translation by blocking the formation of initiation factor complexes. RNA 12: 1825–1834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88. Murphy MB, Fuller ST, Richardson PM, Doyle SA (2003) An improved method for the in vitro evolution of aptamers and applications in protein detection and purification. Nucleic Acids Research 31: e110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89. Piganeau N, Thuillier V, Famulok M (2001) In vitro selection of allosteric ribozymes: theory and experimental validation. Journal of Molecular Biology 312: 1177–1190. [DOI] [PubMed] [Google Scholar]
- 90.Ryu Y, Kim K-J, Roessner CA, Scott AI (2006) Decarboxylative Claisen condensation catalyzed by in vitro selected ribozymes. Chemical Communications: 1439–1441. [DOI] [PubMed]
- 91. Saito H, Kourouklis D, Suga H (2001) An in vitro evolved precursor tRNA with aminoacylation activity. The EMBO Journal 20: 1797–1878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92. Schürer H, Stembera K, Knoll D, Mayer G, Blind M, et al. (2001) Aptamers that bind to the antibiotic moenomycin A. Bioorganic & Medicinal Chemistry 9: 2557–2563. [DOI] [PubMed] [Google Scholar]
- 93. Seelig B, Jäschke A (1999) A small catalytic RNA motif with Diels-Alderase activity. Chemistry & Biology 6: 167–176. [DOI] [PubMed] [Google Scholar]
- 94. Seiwert SD, Stines Nahreini T, Aigner S, Ahn NG, Uhlenbeck OC (2000) RNA aptamers as pathway-specific MAP kinase inhibitors. Chemistry & Biology 7: 833–843. [DOI] [PubMed] [Google Scholar]
- 95. Sengle G, Eisenfuhr A, Arora PS, Nowick JS, Famulok M (2001) Novel RNA catalysts for the Michael reaction. Chem Biol 8: 459–473. [DOI] [PubMed] [Google Scholar]
- 96. Soukup GA, Emilsson GAM, Breaker RR (2000) Altering molecular recognition of RNA aptamers by allosteric selection. Journal of Molecular Biology 298: 623–632. [DOI] [PubMed] [Google Scholar]
- 97. Sun L, Cui Z, Gottlieb RL, Zhang B (2002) A selected ribozyme catalyzing diverse dipeptide synthesis. Chem Biol 9: 619–628. [DOI] [PubMed] [Google Scholar]
- 98. Tahiri-Alaoui A, Frigotto L, Manville N, Ibrahim J, Romby P, et al. (2002) High affinity nucleic acid aptamers for streptavidin incorporated into bi-specific capture ligands. Nucleic Acids Research 30: e45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99. Tang J, Breaker RR (2000) Structural diversity of self-cleaving ribozymes. Proceedings of the National Academy of Sciences of the USA 97: 5784–5789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100. Thomas M, Chédin S, Carles C, Riva M, Famulok M, et al. (1997) Selective targeting and inhibition of yeast RNA polymerase II by RNA aptamers. Journal of Biological Chemistry 272: 27980–27986. [DOI] [PubMed] [Google Scholar]
- 101. Tok JB-H, Cho J, Rando RR (2000) RNA aptamers that specifically bind to a 16S ribosomal RNA decoding region construct. Nucleic Acids Research 28: 2902–2910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102. Tuschl T, Sharp PA, Bartel DP (1998) Selection in vitro of novel ribozymes from a partially randomized U2 and U6 snRNA library. The EMBO Journal 17: 2637–2650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103. Ulrich H, Ippolito JE, Pagán OR, Eterovic VA, Hann RM, et al. (1998) In vitro selection of RNA molecules that displace cocaine from the membrane-bound nicotinic acetylcholine receptor. Proceedings of the National Academy of Sciences 95: 14051–14056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104. Unrau PJ, Bartel DP (1998) RNA-catalysed nucleotide synthesis. Nature 395: 260–263. [DOI] [PubMed] [Google Scholar]
- 105. Urvil PT, Kakiuchi N, Zhou D-M, Shimotohno K, Kumar PKR, et al. (1997) Selection of RNA aptamers that bind specifically to the NS3 protease of hepatitis C virus. European Journal of Biochemistry 248: 130–138. [DOI] [PubMed] [Google Scholar]
- 106. Wallace ST, Schroeder R (1998) In vitro selection and characterization of streptomycin-binding RNAs: recognition discrimination between antibiotics. RNA 4: 112–123. [PMC free article] [PubMed] [Google Scholar]
- 107. Wang Y, Killian J, Hamasaki K, Rando RR (1996) RNA molecules that specifically and stoichiometrically bind aminoglycoside antibiotics with high affinities. Biochemistry 35: 12338–12346. [DOI] [PubMed] [Google Scholar]
- 108. Wecker M, Smith D, Gold L (1996) In vitro selection of a novel catalytic RNA: characterization of a sulfur alkylation reaction and interaction with small peptide. RNA 2: 982–994. [PMC free article] [PubMed] [Google Scholar]
- 109. Weiss S, Proske D, Neumann M, Groschup MH, Kretzschmar HA, et al. (1997) RNA aptamers specifically interact with the prion protein PrP. Journal of Virology 71: 8790–8797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110. Welch M, Majerfeld I, Yarus M (1997) 23S rRNA similarity from selection for peptidyl transferase mimicry. Biochemistry 36: 6614–6623. [DOI] [PubMed] [Google Scholar]
- 111. White RR, Shan S, Rusconi CP, Shetty G, Dewhirst MW, et al. (2003) Inhibition of rat corneal angiogenesis by a nuclease-resistant RNA aptamer specific for angiopoietin-2. Proceedings of the National Academy of Sciences 100: 5028–5033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112. Williams KP, Ciafre S, Tocchini-Valentini GP (1995) Selection of novel Mg2+-dependent self-cleaving ribozymes. The EMBO Journal 14: 4551–4557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113. Zhang B, Cech TR (1997) Peptide bond formation by in vitro selected ribozymes. Nature 390: 96–100. [DOI] [PubMed] [Google Scholar]
- 114. Schuster P, Fontana W, Stadler PF, Hofacker IL (1994) From sequences to shapes and back: a case study in RNA secondary structures. Proceedings of the Royal Society of London B 255: 279–284. [DOI] [PubMed] [Google Scholar]
- 115. Joyce GF (2004) Directed evolution of nucleic acid enzymes. Annual Review of Biochemistry 73: 791–836. [DOI] [PubMed] [Google Scholar]
- 116. Geveretz J, Gan HH, Schlick T (2005) In vitro RNA random pools are not structurally diverse: A computational analysis. RNA 11: 853–863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117. Meyers L, Lee J, Cowperthwaite M, Ellington A (2004) The robustness of naturally and artificially selected nucleic acid secondary structures. Journal of Molecular Evolution 58: 681–691. [DOI] [PubMed] [Google Scholar]
- 118. Hayden EJ, Weikert C, Wagner A (2012) Directional selection causes decanalization in a Group I Ribozyme. PLOS ONE 7: e45351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119. Wagner GP, Altenberg L (1996) Complex adaptations and evolution of evolvability. Evolution 50: 329–347. [DOI] [PubMed] [Google Scholar]
- 120.Wagner A (2005) Robustness and Evolvability in Living Systems Princeton University Press.
- 121. Stich M, Manrubia SC (2011) Motif frequency and evolutionary search times in RNA populations. Journal of Theoretical Biology 280: 117–126. [DOI] [PubMed] [Google Scholar]
- 122.Kun Á, Maurel M-C, Santos M, Szathmáry E (2005) Fitness landscapes, error thresholds, amd cofactors in aptamer evolution. In: Klussmann S, editor. The aptamer handbook. Weinheim: WILEY-VCH Verlag GmbH & Co. KGaA. pp. 54–92. [Google Scholar]
- 123.Maynard Smith J, Szathmáry E (1995) The Major Transition in Evolution. Oxford, UK: W.H. Freeman. [Google Scholar]
- 124.Czárán T, Szathmáry E (2000) Coexistence of replicators in prebiotic evolution. In: Dieckmann U, Law R, Metz JAJ, editors. The Geometry of Ecological Interactions. Cambridge: Cambridge University Press. pp. 116–134. [Google Scholar]
- 125. Könnyű B, Czárán T, Szathmáry E (2008) Prebiotic replicase evolution in a surface-bound metabolic system: parasites as a source of adaptive evolution. BMC Evolutionary Biology 8: 267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126. Könnyű B, Czárán T (2011) The evolution of enzyme specificity in the metabolic replicator model of prebiotic evolution. PLOS ONE 6: e20931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Szathmáry E, Demeter L (1987) Group selection of early replicators and the origin of life. Journal of Theoretical Biology 128.. [DOI] [PubMed] [Google Scholar]
- 128.Hubai AG (2013) Emergence and evolution of primeval metabolic systems. Budapest: Eötvös Loránd University (Supervisor Á. Kun).
- 129. Szabó P, Scheuring I, Czárán T, Szathmáry E (2002) In silico simulations reveal that replicators with limited dispersal evolve towards higher efficiency and fidelity. Nature 420: 340–343. [DOI] [PubMed] [Google Scholar]
- 130. Jones BL, Enns RH, Rangnekar SS (1976) On the theory of selection of coupled macromolecular systems. Bulletin of Mathematical Biology 38: 15–28. [Google Scholar]
- 131. Thompson CJ, McBride JL (1974) On Eigen's theory of the self-organization of matter and the evolution of biological macromolecules. Mathematical biosciences 21: 127–142. [Google Scholar]
- 132. Schuster P, Swetina J (1988) Stationary mutant distributions and evolutionary optimization. Bulletin of Mathematical Biology 50: 635–660. [DOI] [PubMed] [Google Scholar]
- 133. Hernandez V, Roman JE, Vidal V (2005) SLEPc: A scalable and flexible toolkit for the solution of eigenvalue problems. ACM Trans Math Softw 31: 351–362. [Google Scholar]
- 134.Balay S, Buschelman K, Eijkhout V, Gropp WD, Kaushik D, et al.. (2008) PETSc Users Manual. Illinois, USA: Argonne National Laboratory. [Google Scholar]
- 135. Fontana W, Könings DAM, Stadler PF, Schuster P (1993) Statictics of RNA secondary structures. Biopolymers 33: 1389–1404. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Error threshold of real ribozymes and aptamers. RNA sequences of ribozymes and aptamers from the literature is listed alongside their length, number of 1-neighbour neutral mutants, frequency of nearest-neighbour (one-step) neutral mutants (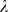 ), the estimated error threshold and the citation for the sequence. Stabilizing selection was applied to selected sequences, and the highest number of 1-neighbour neutral mutants is reported here.
), the estimated error threshold and the citation for the sequence. Stabilizing selection was applied to selected sequences, and the highest number of 1-neighbour neutral mutants is reported here.
(XLSX)
Structural diversity of RNA sequences of length 14 with two letter (GC) and four letter (GCAU) alphabet. Secondary structures in bracket notation are reported with the number of unique sequences folding to this structure. Frequencies of structures among all possible structures of length 14 are reported. The unstructured structure has the highest frequency among the sequences built from four letters. We also report the frequencies of structures if we omit these sequences from the total count.
(XLSX)
Secondary structure classes and Super secondary structure classes of GC sequences of length 16. Secondary structures in bracket notation are reported with the number of unique sequences folding to this structure. The first column show the super secondary structure class (SSSC) without leading and trailing single stranded nucleotides. The second column gives the total number of unique sequences folding into the SSSC. Then in column 3 the individual structures are reported as well as their total unique sequence count (column 4).
(XLSX)
Data Availability Statement
The authors confirm that all data underlying the findings are fully available without restriction. All relevant data are within the paper and its Supporting Information files.