MINIMAX BOUNDS FOR SPARSE PCA WITH NOISY HIGH-DIMENSIONAL DATA

Abstract

We study the problem of estimating the leading eigenvectors of a high-dimensional population covariance matrix based on independent Gaussian observations. We establish a lower bound on the minimax risk of estimators under the l₂ loss, in the joint limit as dimension and sample size increase to infinity, under various models of sparsity for the population eigenvectors. The lower bound on the risk points to the existence of different regimes of sparsity of the eigenvectors. We also propose a new method for estimating the eigenvectors by a two-stage coordinate selection scheme.

1. Introduction

Principal components analysis (PCA) is widely used to reduce dimensionality of multivariate data. A traditional setting involves repeated observations from a multivariate normal distribution. Two key theoretical questions are: (i) what is the relation between the sample and population eigenvectors, and (ii) how well can population eigenvectors be estimated under various sparsity assumptions? When the dimension N of the observations is fixed and the sample size n → ∞, the asymptotic properties of the sample eigenvalues and eigenvectors are well known [Anderson (1963), Muirhead (1982)]. This asymptotic analysis works because the sample covariance approximates the population covariance well when the sample size is large. However, it is increasingly common to encounter statistical problems where the dimensionality N is comparable to, or larger than, the sample size n. In such cases, the sample covariance matrix, in general, is not a reliable estimate of its population counterpart.

Better estimators of large covariance matrices, under various models of sparsity, have been studied recently. These include development of banding and thresholding schemes [Bickel and Levina (2008a, 2008b), Cai and Liu (2011), El Karoui (2008), Rothman, Levina and Zhu (2009)], and analysis of their rate of convergence in the spectral norm. More recently, Cai, Zhang and Zhou (2010) and Cai and Zhou (2012) established the minimax rate of convergence for estimation of the covariance matrix under the matrix l₁ norm and the spectral norm, and its dependence on the assumed sparsity level.

In this paper we consider a related but different problem, namely, the estimation of the leading eigenvectors of the covariance matrix. We formulate this eigenvector estimation problem under the well-studied “spiked population model” which assumes that the ordered set of eigenvalues ℒ(∑) of the population covariance matrix ∑ satisfies

$$ℒ(\sum )=\{{\mathrm{\lambda }}_1+{\mathrm{\sigma }}^2,\dots ,{\mathrm{\lambda }}_M+{\mathrm{\sigma }}^2,{\mathrm{\sigma }}^2,\dots ,{\mathrm{\sigma }}^2\}$$ (1.1)

for some M ≥ 1, where σ² > 0 and λ₁ > λ₂ > ⋯ > λ_M > 0. This is a standard model in several scientific fields, including, for example, array signal processing [see, e.g., van Trees (2002)] where the observations are modeled as the sum of an M-dimensional random signal and an independent, isotropic noise. It also arises as a latent variable model for multivariate data, for example, in factor analysis [Jolliffe (2002), Tipping and Bishop (1999)]. The assumption that the leading M eigenvalues are distinct is made to simplify the analysis, as it ensures that the corresponding eigenvectors are identifiable up to a sign change. The assumption that all remaining eigenvalues are equal is not crucial as our analysis can be generalized to the case when these are only bounded by σ². Asymptotic properties of the eigenvalues and eigenvectors of the sample covariance matrix under this model, in the setting when N/n → c ∈ (0, ∞) as n → ∞, have been studied by Lu (2002), Baik and Silverstein (2006), Nadler (2008), Onatski (2006) and Paul (2007), among others. A key conclusion is that when N/n → c > 0, the eigenvectors of standard PCA are inconsistent estimators of the population eigenvectors.

Eigenvector and covariance matrix estimation are related in the following way. When the population covariance is a low rank perturbation of the identity, as in this paper, sparsity of the eigenvectors corresponding to the nonunit eigenvalues implies sparsity of the whole covariance. Consistency of an estimator of the whole covariance matrix in spectral norm implies convergence of its leading eigenvalues to their population counterparts. If the gaps between the distinct eigenvalues remain bounded away from zero, it also implies convergence of the corresponding eigen-subspaces [El Karoui (2008)]. In such cases, upper bounds for sparse covariance estimation in the spectral norm, as in Bickel and Levina (2008a) and Cai and Zhou (2012), also yield upper bounds on the rate of convergence of the corresponding eigenvectors under the l₂ loss. These works, however, did not study the following fundamental problem, considered in this paper: How well can the leading eigenvectors be estimated, and namely, what are the minimax rates for eigenvector estimation? Indeed, it turns out that the optimal rates for covariance matrix estimation and leading eigenvector estimation are different. Moreover, schemes based on thresholding the entries of the sample covariance matrix do not achieve the minimax rate for eigenvector estimation. The latter result is beyond the scope of this paper and will be reported in a subsequent publication by the current authors.

Several works considered various models of sparsity for the leading eigenvectors and developed improved sparse estimators. For example, Witten, Tibshirani and Hastie (2009) and Zou, Hastie and Tibshirani (2006), among others, imposed l₁-type sparsity constraints directly on the eigenvector estimates and proposed optimization procedures for obtaining them. Shen and Huang (2008) suggested a regularized low rank approach to sparse PCA. The consistency of the resulting leading eigenvectors was recently proven in Shen, Shen and Marron (2011), in a model in which the sample size n is fixed while N → ∞. d’Aspremont et al. (2007) suggested a semi-definite programming (SDP) problem as a relaxation to the l₀-penalty for sparse population eigenvectors. Assuming a single spike, Amini and Wainwright (2009) studied the asymptotic properties of the resulting leading eigenvector of the covariance estimator in the joint limit as both sample size and dimension tend to infinity. Specifically, they considered a leading eigenvector with exactly k ≪ N nonzero entries all of the form $\{-1/\sqrt{k},1/\sqrt{k}\}$. For this hardest subproblem in the k-sparse l₀-ball, Amini and Wainwright (2009) derived information theoretic lower bounds for such eigenvector estimation.

In this paper, in contrast, following Johnstone and Lu (2009) (JL), we study estimation of the leading eigenvectors of ∑ assuming that these are approximately sparse, with a bounded l_q norm. Under this model, JL developed an estimation procedure based on coordinate selection by thresholding the diagonal of the sample covariance matrix, followed by the spectral decomposition of the submatrix corresponding to the selected coordinates. JL further proved consistency of this estimator assuming dimension grows at most polynomially with sample size, but did not study its convergence rate. Since this estimation procedure is considerably simpler to implement and computationally much faster than the l₁ penalization procedures cited above, it is of interest to understand its theoretical properties. More recently, Ma (2011) developed iterative thresholding sparse PCA(ITSPCA),which is based on repeated filtering, thresholding and orthogonalization steps that result in sparse estimators of the subspaces spanned by the leading eigenvectors. He also proved consistency and derived rates of convergence under appropriate loss functions and sparsity assumptions. In a later work, Cai, Ma and Wu (2012) considered a two-stage estimation scheme for the leading population eigenvector, in which the first stage is similar to the DT scheme applied to a stochastically perturbed version of the data. The estimates of the leading eigenvectors from this step are then used to project another stochastically perturbed version of the data to obtain the final estimates of the eigenvectors through solving an orthogonal regression problem. They showed that this two-stage scheme achieves the optimal rate for estimation of eigen-subspaces under suitable sparsity conditions.

In this paper, which is partly based on the Ph.D. thesis of Paul [Paul (2005)], we study the estimation of the leading eigenvectors of ∑, all assumed to belong to appropriate l_q spaces. Our analysis thus extends the JL setting and complements the work of Amini and Wainwright (2009) in the l₀-sparsity setting. For simplicity, we assume Gaussian observations in our analysis.

The main contributions of this paper are as follows. First, we establish lower bounds on the rate of convergence of the minimax risk for any eigenvector estimator under the l₂ loss. This analysis points to three different regimes of sparsity, which we denote dense, thin and sparse, each having its own rate of convergence. We show that in the “dense” setting (as defined in Section 3), the standard PCA estimator attains the optimal rate of convergence, whereas in sparser settings it is not even consistent. Next, we show that while the JL diagonal thresholding (DT) scheme is consistent under these sparsity assumptions, it is not rate optimal in general. This motivates us to propose a new refined thresholding method (Augmented Sparse PCA, or ASPCA) that is based on a two-stage coordinate selection scheme. In the sparse setting, both our ASPCA procedure, as well as the method of Ma (2011) achieve the lower bound on the minimax risk obtained by us, and are thus rate-optimal procedures, so long as DT is consistent. For proofs see Ma (2011) and Paul and Johnstone (2007). There is a somewhat special, intermediate, “thin” region where a gap exists between the current lower bound and the upper bound on the risk. It is an open question whether the lower bound can be improved in this scenario, or a better estimator can be derived. Table 1 provides a comparison of the lower bounds and rates of convergence of various estimators.

Table 1.

Comparison of lower bounds on eigenvector estimation and worst case rates of various procedures

Estimator Lower bound	Dense O(N/n)	Thin O(n−(1−q/2))	Sparse O((log N/n)1−q/2)
PCA	Rate optimal*	Inconsistent	Inconsistent
DT	Inconsistent	Inconsistent	Not rate optimal
ASPCA	Inconsistent	Inconsistent	Rate optimal†

^*When N/n → 0.

^†So long as DT is consistent.

The theoretical results also show that under comparable scenarios, the optimal rate for eigenvector estimation O((log N/n)^−(1−q/2)) (under squared-error loss) is faster than the rate obtained for sparse covariance estimation, O((log N/n)^−(1−q)) (under squared operator norm loss), by Bickel and Levina (2008a) and shown to be optimal by Cai and Zhou (2012).

Finally, we emphasize that to obtain good finite-sample performance for both our two-stage scheme, as well as for other thresholding methods, the exact thresholds need to be carefully tuned. This issue and the detailed theoretical analysis of the ASPCA estimator are beyond the scope of this paper, and will be presented in a future publication. After this paper was completed, we learned of Vu and Lei (2012), which cites Paul and Johnstone (2007) and contains results overlapping with some of the work of Paul and Johnstone (2007) and this paper.

The rest of the paper is organized as follows. In Section 2, we describe the model for the eigenvectors and analyze the risk of the standard PCA estimator. In Section 3, we present the lower bounds on the minimax risk of any eigenvector estimator. In Section 4, we derive a lower bound on the risk of the diagonal thresholding estimator proposed by Johnstone and Lu (2009). In Section 5, we propose a new estimator named ASPCA (augmented sparse PCA) that is a refinement of the diagonal thresholding estimator. In Section 6, we discuss the question of attainment of the risk bounds. Proofs of the results are given in Appendix A.

Throughout, 𝕊^N−1 denotes the unit sphere in ℝ^N centered at the origin, ⌊x⌋ denotes the largest integer less than or equal to x ∈ ℝ.

2. Problem setup

We suppose a triangular array model, in which for each n, the random vectors $X_i≔X_i^n,i=1,\dots ,n$, each have dimension N = N(n) and are independent and identically distributed on a common probability space. Throughout we assume that X_i’s are i.i.d. as N_N(0, ∑), where the population matrix ∑, also depending on N, is a finite rank perturbation of (a multiple of) the identity. In other words,

$$\sum =\sum _{\nu =1}^M{\mathrm{\lambda }}_{\nu }{\theta }_{\nu }{\theta }_{\nu }^T+{\mathrm{\sigma }}^{2}I,$$ (2.1)

where λ₁ > λ₂ > ⋯ > λ_M > 0, and the vectors θ₁, … ,θ_M ∈ ℝ^N are orthonormal, which implies (1.1). θ_ν is the eigenvector of ∑ corresponding to the νth largest eigenvalue, namely, λ_ν + σ². The term “finite rank” means that M remains fixed even as n → ∞. The asymptotic setting involves letting both n and N grow to infinity simultaneously. For simplicity, we assume that the λ_ν’s are fixed while the parameter space for the θ_ν’s varies with N.

The observations can be described in terms of the model

$$X_{ik}=\sum _{\nu =1}^M\sqrt{{\mathrm{\lambda }}_{\nu }}{\upsilon }_{\nu i}{\theta }_{\nu k}+\mathrm{\sigma }{Z}_{ik},i=1,\dots ,n,k=1,\dots ,N.$$ (2.2)

Here, for each i, υ_νi, Z_ik are i.i.d. N(0, 1). Since the eigenvectors of ∑ are invariant to a scale change in the original observations, it is henceforth assumed that σ = 1. Hence, λ₁, …, λ_M in the asymptotic results should be replaced by λ₁/σ², … , λ_M/σ² when (2.1) holds with an arbitrary σ > 0. Since the main focus of this paper is estimation of eigenvectors, without loss of generality we consider the uncentered sample covariance matrix S ≔ n⁻¹ XX^T, where X = [X₁: … : X_n].

The following condition, termed Basic assumption, will be used throughout the asymptotic analysis, and will be referred to as (BA).

(BA) (2.2) holds with σ = 1; N = N(n) → ∞ as n → ∞; λ₁ > ⋯ > λ_M > 0 are fixed (do not vary with N); M is unknown but fixed.

2.1. Eigenvector estimation with squared error loss

Given data ${\{X_i\}}_{i=1}^n$, the goal is to estimate M and the eigenvectors θ₁, … ,θ_M. For simplicity, to derive the lower bounds, we first assume that M is known. In Section 5.2 we derive an estimator of M, which can be shown to be consistent under the assumed sparsity conditions. To assess the performance of any estimator, a minimax risk analysis approach is proposed. The first task is to specify a loss function L(θ̂_ν, θ_ν) between the estimated and true eigenvector.

Eigenvectors are invariant to choice of sign, so we introduce a notation for the acute (angle) difference between unit vectors,

$$\mathbf{a}⊝\mathbf{b}=\mathbf{a}-\text{sign}(\langle \mathbf{a},\mathbf{b}\rangle )\mathbf{b},$$

where a and b are N × 1 vectors with unit l₂ norm. We consider the following loss function, also invariant to sign changes:

$$L(\mathbf{a},\mathbf{b})≔2(1-|\langle \mathbf{a},\mathbf{b}\rangle |)={\Vert \mathbf{a}⊝\mathbf{b}\Vert }^2.$$ (2.3)

An estimator θ̂_ν is called consistent with respect to L, if L(θ̂_ν,θ_ν) → 0 in probability as n → ∞.

2.2. Rate of convergence for ordinary PCA

We first consider the asymptotic risk of the leading eigenvectors of the sample covariance matrix (henceforth referred to as the standard PCA estimators) when the ratio N/n → 0 as n → ∞. For future use, we define

$$h(\mathrm{\lambda })≔\frac{{\mathrm{\lambda }}^2}{1+\mathrm{\lambda }},\mathrm{\lambda }>0,$$ (2.4)

and

$$g(\mathrm{\lambda },\mathrm{\tau })=\frac{{(\mathrm{\lambda }-\mathrm{\tau })}^2}{(1+\mathrm{\lambda })(1+\mathrm{\tau })},\mathrm{\lambda },\mathrm{\tau }>0.$$ (2.5)

In Johnstone and Lu (2009) (Theorem 1) it was shown that under a single spike model, as N/n → 0, the standard PCA estimator of the leading eigenvector is consistent. The following result, proven in the Appendix, is a refinement of that, as it also provides the leading error term.

Theorem 2.1. Let θ̂_ν,PCA be the eigenvector corresponding to the νth largest eigenvalue of S. Assume that (BA) holds and N, n → ∞ such that N/n → 0. Then, for each ν = 1, … , M,

$$\underset{{\theta }_{\nu }\in {𝕊}^{N-1}}{\text{sup}}𝔼L({\widehat{\theta }}_{\nu ,\text{PCA}},{\theta }_{\nu })=[\frac{N-M}{nh({\mathrm{\lambda }}_{\nu })}+\frac{1}{n}\sum _{\mu \ne \nu }\frac{1}{g({\mathrm{\lambda }}_{\mu },{\mathrm{\lambda }}_{\nu })}](1+o(1)).$$ (2.6)

Remark 2.1. Observe that Theorem 2.1 does not assume any special structure such as sparsity for the eigenvectors. The first term on the right-hand side of (2.6) is a nonparametric component which arises from the interaction of the noise terms with the different coordinates. The second term is “parametric” and results from the interaction with the remaining M − 1 eigenvectors corresponding to different eigenvalues. The second term shows that the closer the successive eigenvalues, the larger the estimation error. The upshot of (2.6) is that standard PCA yields a consistent estimator of the leading eigenvectors of the population covariance matrix when the dimension-to-sample-size ratio (N/n) is asymptotically negligible.

2.3. l_q constraint on eigenvectors

When N/n → c ∈ (0, ∞], standard PCA provides inconsistent estimators for the population eigenvectors, as shown by various authors [Johnstone and Lu (2009), Lu (2002), Nadler (2008), Onatski (2006), Paul (2007)]. In this subsection we consider the following model for approximate sparsity of the eigenvectors. For each ν = 1, … , M, assume that θ_ν belongs to an l_q ball with radius C, for some q ∈ (0, 2), thus θ_ν ∈ Θ_q (C), where

$${\mathrm{\Theta }}_q(C)≔\{\mathbf{a}\in {𝕊}^{N-1}:\sum _{k=1}^N{|a_k|}^q\le C^q\}.$$ (2.7)

Note that our condition of sparsity is slightly different from that of Johnstone and Lu (2009). Since 0 < q < 2, for Θ_q(C) to be nonempty, one needs C ≥ 1. Further, if C_q ≥ N_1−q/2, then the space Θ_q (C) is all of 𝕊^N−1 because in this case, the least sparse vector $\frac{1}{\sqrt{N}}$ (1, 1, … , 1) is in the parameter space.

The parameter space for θ ≔ [θ₁: … :θ_M] is denoted by

$${\mathrm{\Theta }}_q^M(C_1,\dots ,C_M)≔\{\mathbf{\theta }\in \prod _{\nu =1}^M{\mathrm{\Theta }}_q(C_{\nu }):\langle {\theta }_{\nu },{\theta }_{\nu \prime }\rangle =0,\text{for}\nu \ne \nu \prime \},$$ (2.8)

where Θ_q (C) is defined through (2.7), and C_ν ≥ 1 for all ν = 1, … , M. Thus ${\mathrm{\Theta }}_q^M$ consists of sparse orthonormal M-frames, with sparsity measured in l_q. Note that in the analysis that follows we allow the C_ν’s to increase with N.

Remark 2.2. While our focus is on eigenvector sparsity, condition (2.8) also implies sparsity of the covariance matrix itself. In particular, for q ∈ (0, 1), a spiked covariance matrix satisfying (2.8) also belongs to the class of sparse covariance matrices analyzed by Bickel and Levina (2008a), Cai and Liu (2011) and Cai and Zhou (2012). Indeed, Cai and Zhou (2012) obtained the minimax rate of convergence for covariance matrix estimators under the spectral norm when the rows of the population matrix satisfy a weak-l_q constraint. However, as we will show below, the minimax rate for estimation of the leading eigenvectors is faster than that for covariance estimation.

3. Lower bounds on the minimax risk

We now derive lower bounds on the minimax risk of estimating θ_ν under the loss function (2.3). To aid in describing and interpreting the lower bounds, we define the following two auxiliary parameters. The first is an effective noise level per coordinate

$${\tau }_{\nu }^2=1/(nh({\mathrm{\lambda }}_{\nu }))$$ (3.1)

and the second is an effective dimension

$$m_{\nu }≔A_q{({\overline{C}}_{\nu }/{\tau }_{\nu })}^q,$$ (3.2)

where a_q ≔ (2/9)^1−q/2, c₁ ≔ log(9/8) and $A_q≔1/(a_q{c}_1^{q/2})$ and finally ${\overline{C}}_{\nu }^q≔C_{\nu }^q-1$.

The phrase effective noise level per coordinate is motivated by the risk bound in Theorem 2.1: dividing both sides of (2.6) by N, the expected “per coordinate” risk (or variance) of the PCA estimator is asymptotically ${\tau }_{\nu }^2$. Next, following Nadler (2009), let us provide a different interpretation of τ_ν. Consider a sparse θ_ν and an oracle that, regardless of the observed data, selects a set J_τ of all coordinates of θ_ν that are larger than τ in absolute value, and then performs PCA on the sample covariance restricted to these coordinates. Since θ_ν ∈ Θ_q (C_ν), the maximal squared-bias is

$$\underset{{\theta }_{\nu }\in {\mathrm{\Theta }}_q(C_{\nu })}{\text{sup}}\sum _{k\notin J_{\tau }}{|{\theta }_{\nu k}|}^2\asymp \text{sup}\{\sum _{k=1}^N{x}_k^{2/q}:\sum _{k=1}^N{x}_k\le C_{\nu }^q,0\le x_k\le {\tau }^q\}\asymp C_{\nu }^q{\tau }^{2-q},$$

which follows by the correspondence x_k = |θ_νk|^q, and the convexity of the function ${\sum }_{k=1}^N{x}_k^{2/q}$. On the other hand, by Theorem 2.1, the maximal variance term of this oracle estimator is of the order k_τ /(nh(λ_ν)) where k_τ is the maximal number of coordinates of θ_ν exceeding τ. Again, θ_ν ∈ Θ_q (C_ν) implies that $k_{\tau }\asymp C_{\nu }^q{\tau }^{-q}$. Thus, to balance the bias and variance terms, we need $\tau \asymp 1/\sqrt{nh({\mathrm{\lambda }}_{\nu })}={\tau }_{\nu }$. This heuristic analysis shows that τ_ν can be viewed as an oracle threshold for the coordinate selection scheme, that is, the best possible estimator of θ_ν based on individual coordinate selection can expect to recover only those coordinates that are above the threshold τ_ν.

To understand why m_ν is an effective dimension, consider the least sparse vector θ_ν ∈ Θ_q (C_ν). This vector should have as many nonzero coordinates of equal size as possible. If $C_{\nu }^q>N^{1-q/2}$ then the vector with coordinates ± N^−1/2 does the job. Otherwise, we set the first coordinate of the vector to be $\sqrt{1-r^2}$ for some r ∈ (0, 1) and choose all the nonzero coordinates to be of magnitude τ_ν. Clearly, we must have $r^2=m{\tau }_{\nu }^2$, where m + 1 is the maximal number of nonzero coordinates, while the l_q constraint implies that ${(1-r^2)}^{q/2}+m{\tau }_{\nu }^q\le C_{\nu }^q$. The last inequality shows that the maximal m is just a constant multiple of m_ν. This construction also constitutes the key idea in the proof of Theorems 3.1 and 3.2. Finally, we set

$$N\prime =N-M.$$ (3.3)

Theorem 3.1. Assume that (BA) holds, 0 < q < 2 and n, N → ∞. Then, there exists a constant B₁ > 0 such that for n sufficiently large,

$$R_{\nu }^{*}≔\underset{{\widehat{\theta }}_{\nu }}{\text{inf}}\underset{{\mathrm{\Theta }}_q(\mathbf{C})}{\text{sup}}𝔼L({\widehat{\theta }}_{\nu },{\theta }_{\nu })\ge B_1{\delta }_n,$$ (3.4)

where δ_n is given by

$${\delta }_n=\{\begin{array}{ccc}{\tau }_{\nu }^{2}N\prime ,\hfill & \mathit{\text{if}}{\tau }_{\nu }^{2}N\prime <1\mathit{\text{and}}N\prime <m_{\nu }\hfill & (\mathit{\text{dense setting}}),\hfill \\ {\tau }_{\nu }^2{m}_{\nu },\hfill & \mathit{\text{if}}{\tau }_{\nu }^2{m}_{\nu }<1\mathit{\text{and}}{m}_{\nu }<N\prime \hfill & (\text{sparse setting}),\hfill \\ 1,\hfill & \mathit{\text{if}}{\tau }_{\nu }^2·\text{min}\{N\prime m_{\nu }\}>1\hfill & (\mathit{\text{weak signal}}).\hfill \end{array}$$

We may think of m_{n, ν} ≔ min{N′, m_ν} as the effective dimension of the least favorable configuration.

In the thin setting, $m_{n,\nu }=A_q{\overline{C}}_{\nu }^q{[nh({\mathrm{\lambda }}_{\nu })]}^{q/2}<N(\mathrm{i}.\mathrm{e}.,{\overline{C}}_{\nu }^q{n}^{q/2}<c\prime N$ for some c′ > 0), and the lower bound is of the order

$${\delta }_n=A_q{\overline{C}}_{\nu }^q{\tau }_{\nu }^{2-q}=\frac{A_q{\overline{C}}_{\nu }^q}{{[nh({\mathrm{\lambda }}_{\nu })]}^{1-q/2}}\asymp \frac{{\overline{C}}_{\nu ,n}^q}{n^{1-q/2}}.$$ (3.5)

In the dense setting, on the other hand, m_{n, ν} = N − M, and

$${\delta }_n=\frac{N-M}{nh({\mathrm{\lambda }}_{\nu })}\asymp \frac{N}{n}.$$ (3.6)

If N/n → c for some c > 0, then δ_n ≍ 1, and so any estimator of the eigenvector θ_ν is inconsistent. If N/n → 0, then equation (3.6) and Theorem 2.1 imply that the standard PCA estimator θ̂_ν,PCA attains the optimal rate of convergence.

A sharper lower bound is possible if ${\overline{C}}_{\nu }^q{n}^{q/2}=O(N^{1-\alpha })$ for some α ∈ (0, 1). We call this a sparse setting, noting that it is a special case of the thin setting. In this case the dimension N is much larger than the quantity ${\overline{C}}_{\nu }^q{n}^{q/2}$ measuring the effective dimension. Hence, we define a modified effective noise level percoordinate

$${\overline{\tau }}_{\nu }^2=\frac{\alpha }{9}\frac{\text{log}N}{nh({\mathrm{\lambda }}_{\nu })},$$

and a modified effective dimension

$${\overline{m}}_{\nu }=a_q^{-1}{({\overline{C}}_{\nu }/{\overline{\tau }}_{\nu })}^q.$$

Theorem 3.2. Assume that (BA) holds, 0 < q < 2 and n, N → ∞ in such a way that ${\overline{C}}_{\nu }^q{n}^{q/2}=O(N^{1-\alpha })$ for some α ∈ (0, 1). Then there exists a constant B₁ such that for n sufficiently large, the minimax bound (3.4) holds with

$${\delta }_n={\overline{m}}_{\nu }{\overline{\tau }}_{\nu }^2=a_q^{-1}{C}_{\nu }^q{\left(\frac{\text{log}N}{nh({\mathrm{\lambda }}_{\nu })}\right)}^{1-q/2}(\mathit{\text{sparse setting}})$$ (3.7)

so long as this quantity is ≤ 1.

Note that in the sparse setting δ_n is larger by a factor of (log N)^1−q/2 compared to the thin setting [equation (3.5)].

It should be noted that for fixed signal strength λ_ν, for the corresponding eigenvector to be thin, but not sparse is somewhat of a “rarity,” as the following argument shows: consider first the case N = o(n). If $N\prime <A_q{(h({\mathrm{\lambda }}_{\nu }))}^{q/2}{\overline{C}}_{\nu }^q{n}^{q/2}$, then we are in the dense setting, since ${\tau }_{\nu }^{2}N\prime \asymp N/n\to 0$. On the other hand, if N = o(n) and ${\overline{C}}_{\nu }^q{n}^{q/2}=O(N^{1-\alpha })$ for some α ∈ (0, 1), then θ_ν is sparse, according to the discussion preceding Theorem 3.2. So, if N = o (n), for the eigenvector θ_ν to be thin but not sparse, we need ${\overline{C}}_{\nu }^q{n}^{q/2}\asymp N{s}_N$ where s_N is a term which may be constant or may converge to zero at a rate slower than any polynomial in N. Next, consider the case n = o (N). For a meaningful lower bound, we require ${\tau }_{\nu }^2{m}_{\nu }<1$, which means that ${\overline{C}}_{\nu }^q{n}^{q/2}<c_{q,\nu }n$ for some constant c_q,ν > 0. Thus, as long as n = O(N^1−α) for some α ∈ (0, 1), θ_ν cannot be thin but not sparse. Finally, suppose that N ≍ n, and let ${\overline{C}}_{\nu }^q=N^{\beta }$ for some β ≥ 0. If β < 1 − q/2, then we are in the sparse case. On the other hand, if β > 1 − q/2, then there is no sparsity at all since when $C_{\nu }^q\ge N^{1-q/2}$ the entire 𝕊^N−1 belongs to the relevant l_q ball for θ_ν. Hence, only if β = 1 − q/2 exactly, it is possible for θ_ν to be sparse. This analysis emphasizes the point that at least for a fixed signal strength, thin but not sparse is a somewhat special situation.

4. Risk of the diagonal thresholding estimator

In this section, we analyze the convergence rate of the diagonal thresholding (DT) approach to sparse PCA proposed by Johnstone and Lu (2009) (JL). In this section and in Section 5, we assume for simplicity that N ≥ n. Let the sample variance of the kth coordinate, the kth diagonal entry of S, be denoted by S_kk. Then DT consists of the following steps:

1. Define I = I (γ_n) to be the set of indices k ∈ {1, … , N} such that S_kk > 1 + γ_n for some threshold γ_n > 0.

2. Let S_II be the submatrix of S corresponding to the coordinates I. Perform an eigen-analysis of S_II and denote its eigenvectors by f_i, i = 1, … , min{n, |I|}.

3. For ν = 1, … , M, estimate θ_ν by the N × 1 vector f̃_ν, obtained from f_ν by augmenting zeros to all the coordinates in I^c ≔ {1, … , N} \ I.

Assuming that θ_ν ∈ Θ_q(C_ν), and a threshold ${\gamma }_n=\gamma \sqrt{\text{log}N/n}$ for some γ > 0, JL showed that DT yields a consistent estimator of θ_ν, but did not further analyze the risk. Indeed, as we prove below, the risk of the DT estimator is not rate optimal. This might be anticipated from the lower bound on the minimax risk (Theorems 3.1 and 3.2) which indicate that to attain the optimal risk, a coordinate selection scheme must select all coordinates of θ_ν of size at least $c\sqrt{\text{log}N/n}$ for some c > 0. With a threshold of the form γ_n above, however, only coordinates of size (log N/n)^1/4 are selected. Even for the case of a single signal, M = 1, this leads to a much larger lower bound.

Theorem 4.1. Suppose that (BA) holds with M = 1. Let C > 1 (may depend on n), 0 < q < 2 and n, N → ∞ be such that $C^q{n}^{q/4}=o(\sqrt{n})$. Then the diagonal thresholding estimator θ̂_{1, DT} satisfies

$$\underset{{\theta }_1\in {\mathrm{\Theta }}_q(C)}{\text{sup}}𝔼L({\widehat{\theta }}_{1,\text{DT}},{\theta }_1)\ge K_q{\overline{C}}^q{n}^{-(1-q/2)/2}$$ (4.1)

for a constant K_q > 0, where C̄^q = C^q −1.

A comparison of (4.1) with the lower bound (3.5), shows a large gap between the two rates, n^{−1/2(1−q/2)} versus n^−(1−q/2). This gap arises because DT uses only the diagonal of the sample covariance matrix S, ignoring the information in its off diagonal entries. In the next section we propose a refinement of the DT scheme, denoted ASPCA, that constructs an improved eigenvector estimate using all entries of S.

In the sparse setting, the ITSPCA estimator of Ma (2011) attains the same asymptotic rate as the lower bound of Theorem 3.2, provided DT yields consistent estimates of the eigenvectors. The latter condition can be shown to hold if, for example, $C_{\nu }^q{n}^{q/4}{(\text{log}N)}^{1-q/2}=o(\sqrt{n})$ for all ν = 1, … , M. Thus, in the sparse setting, with this additional restriction, the lower bound on the minimax rate is sharp, and consequently, the DT estimator is not rate optimal.

5. A two-stage coordinate selection scheme

As discussed above, the DT scheme can reliably detect only those eigenvector coordinates k for which |θ_ν,k| ≥ c(log N/n)^1/4 (for some c > 0), whereas to reach the lower bound one needs to detect those coordinates for which |θ_ν,k| ≥ c(log N/n)^1/2.

To motivate an improved coordinate selection scheme, consider the single component (i.e., M = 1) case, and form a partition of the N coordinates into two sets A and B, where the former contains all those k such that |θ_1k| is “large” (selected by DT), and the latter contains the remaining smaller coordinates. Partition the matrix ∑ as

$$\sum =\left[\begin{array}{cc}{\sum }_{AA}\hfill & {\sum }_{AB}\hfill \\ {\sum }_{BA}\hfill & {\sum }_{BB}\hfill \end{array}\right].$$

Observe that ${\sum }_{BA}={\mathrm{\lambda }}_1{\theta }_{1,B}{\theta }_{1,A}^T$. Let θ̃₁ be a “preliminary” estimator of θ₁ such that lim_{n → ∞} ℙ(〈θ̃_1,A, θ_1,A〉 ≥ δ₀) = 1 for some δ₀ > 0 (e.g., θ̃₁ could be the DT estimator). Then we have the relationship

$${\sum }_{BA}{\tilde{\theta }}_{1,A}=\langle {\tilde{\theta }}_{1,A},{\theta }_{1,A}\rangle {\mathrm{\lambda }}_1{\theta }_{1,B}\approx c({\delta }_0){\mathrm{\lambda }}_1{\theta }_{1,B}$$

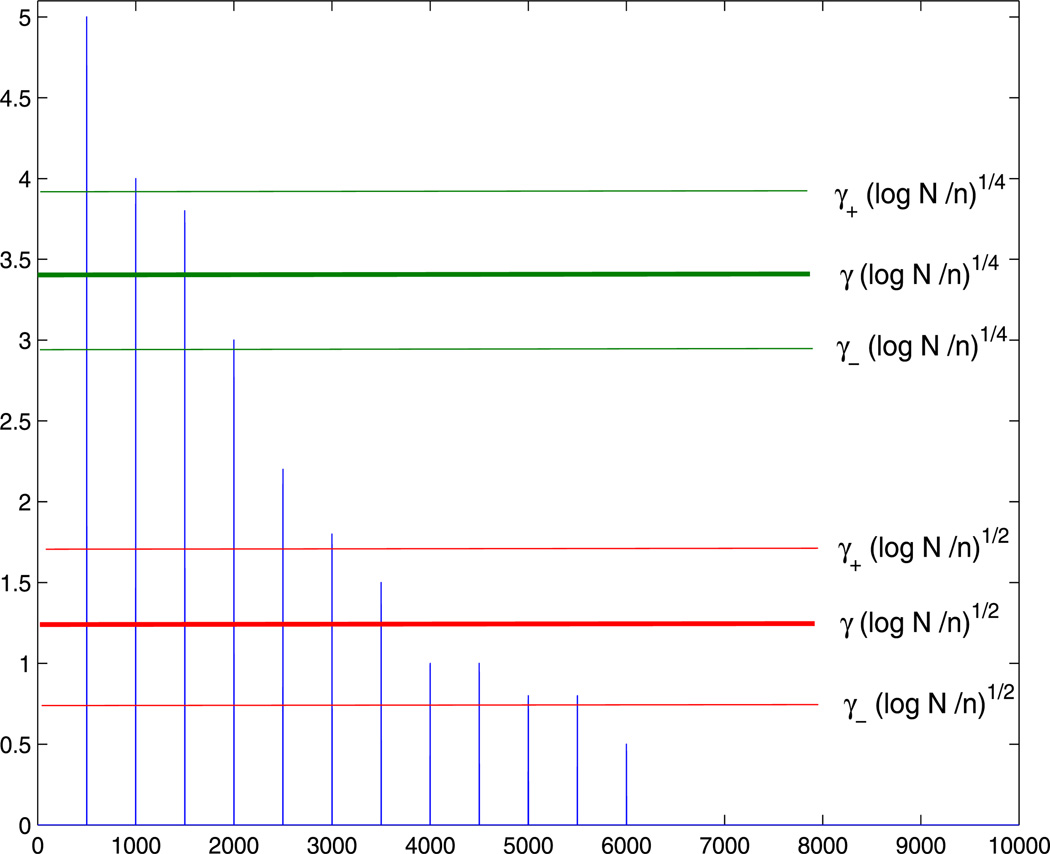
for some c(δ₀) bounded below by δ₀/2, say. Thus one possible strategy is to additionally select all those coordinates of ∑_BAθ̃_1,A that are larger (in absolute value) than some constant multiple of $\sqrt{\text{log}N}/\sqrt{nh({\mathrm{\lambda }}_1)}$. Neither ∑_BA nor λ₁ is known, but we can use S_BA as a surrogate for the former and the largest eigenvalue of S_AA to obtain an estimate for the latter. A technical challenge is to show that, with probability tending to 1, such a scheme indeed recovers all coordinates k with $|{\theta }_{1k}|>{\gamma }_{+}\sqrt{\text{log}N}/\sqrt{nh({\mathrm{\lambda }}_1)}$, while discarding all coordinates k with $|{\theta }_{1k}|<{\gamma }_{-}\sqrt{\text{log}N}/\sqrt{nh({\mathrm{\lambda }}_1)}$ for some constants γ₊ > γ₋ > 0. Figure 1 provides a pictorial description of the DT and ASPCA coordinate selection schemes.

Fig. 1.

Schematic diagram of the DT and ASPCA thresholding schemes under the single component setting. The x-axis represents the indices of different coordinates of the first eigenvector and the vertical lines depict the absolute values of the coordinates. The threshold for the DT scheme is γ(log N/n)^1/4 while the thresholds for the ASPCA scheme is γ(log N/n)^1/2. For some generic constants γ₊ > γ > γ₋ > 0, with high probability, the schemes select all coordinates above the upper limits (indicated by the multiplier γ₊) and discard all coordinates below the lower limits (indicated by the multiplier γ₋).

5.1. ASPCA scheme

Based on the ideas described above, we now present the ASPCA algorithm. It first makes two stages of coordinate selection, whereas the final stage consists of an eigen-analysis of the submatrix of S corresponding to the selected coordinates. The algorithm is described below.

For any γ > 0 define

$$I(\gamma )=\{k:{\mathbf{S}}_{kk}>1+\gamma \}.$$ (5.1)

Let γ_i > 0 for i = 1, 2 and κ > 0 be constants to be specified later.

Stage 1.

• 1°Let I = I (γ_1,n) where ${\gamma }_{1,n}={\gamma }_1\sqrt{\text{log}N/n}.$.
• 2°Denote the eigenvalues and eigenvectors of S_II by ℓ̂₁ > ⋯ > ℓ̂_m1 and f₁, … , f_m1, respectively, where m₁ = min{n, |I|}.
• 3°Estimate M by M̂ defined in Section 5.2.

Stage 2.

• 4°Let $\mathbf{E}=[{\widehat{\ell }}_1^{-1/2}{\mathbf{f}}_1\cdots {\widehat{\ell }}_{\widehat{M}}^{1/2}{\mathbf{f}}_{\widehat{M}}]$ and Q = S_IcI E.
• 5°Let $J=\{k\notin I:{({\mathbf{\text{QQ}}}^T)}_{kk}>{\gamma }_{2,n}^2\}$ for some γ_2,n > 0. Define K = I ∪ J.

Stage 3.

• 6°For ν = 1, …, M̂, denote by θ̂_ν the νth eigenvector of S_KK, augmented with zeros in the coordinates K^c.

Remark 5.1. The ASPCA scheme is specified up to the choice of parameters γ₁ and γ_2,n that determine its rate of convergence. It can be shown that choosing γ₁ = 4 and

$${\gamma }_{2,n}=\kappa \sqrt{\frac{\text{log}N}{n}}+\sqrt{\frac{\widehat{M}}{n}}$$ (5.2)

with $\kappa =\sqrt{3+\epsilon }$ for some ε > 0, results in an asymptotically optimal rate. Again, we note that for finite N, n, the actual performance in terms of the risk of the resulting eigenvector estimate may have a strong dependence on the threshold. In practice, a delicate choice of thresholds can be highly beneficial. This issue, as well as the analysis of the risk of the ASPCA estimator, are beyond the scope of this paper and will be studied in a separate publication.

5.2. Estimation of M

Estimation of the dimension of the signal subspace is a classical problem. If the signal eigenvalues are strong enough (i.e., ${\mathrm{\lambda }}_{\nu }>c\sqrt{N/n}$ for all ν = 1, … , M, for some c > 1 independent of N, n), then nonparametric methods that do not assume eigenvector sparsity can asymptotically estimate the correct M; see, for example, Kritchman and Nadler (2008). When the eigenvectors are sparse, we can detect much weaker signals, as we describe below.

We estimate M by thresholding the eigenvalues of the submatrix S_ĪĪ where $\overline{I}≔I(\overline{\gamma }\sqrt{\text{log}N/n})$ for some γ̄ ∈ (0, γ₁). Let m̄ = min{n, |Ī|} and ℓ̄₁ > ⋯ > ℓ̄_m̄ be the nonzero eigenvalues of S_ĪĪ. Let α_n > 0 be a threshold of the form

$${\alpha }_n=2\sqrt{\frac{|\overline{I}|}{n}}+(1+co\sqrt{\frac{\text{log}n}{n}})\frac{|\overline{I}|}{n}$$

for some user-defined constant c₀ > 0. Then, define M̂ by

$$\widehat{M}≔\text{max}\{1\le k\le \overline{m}:{\overline{\ell }}_k>1+{\alpha }_n\}.$$ (5.3)

The idea is that, for large enough n, I (γ_n) ⊂ Ī with high probability and thus |Ī| acts as an upper bound on |I (γ_1n)|. Using this and the behavior of the extreme eigenvalues of a Wishart matrix, it can be shown that, with a suitable choice of c₀ and γ̄, M̂ is a consistent estimator of M.

6. Summary and discussion

In this paper we have derived lower bounds on eigenvector estimates under three different sparsity regimes, denoted dense, thin and sparse. In the dense setting, Theorems 2.1 and 3.1 show that when N/n → 0, the standard PCA estimator attains the optimal rate of convergence.

In the sparse setting, Theorem 3.1 of Ma (2011) shows that the maximal risk of the ITSPCA estimator proposed by him attains the same asymptotic rate as the corresponding lower bound of Theorem 3.2. This implies that in the sparse setting, the lower bound on the minimax rate is indeed sharp. In a separate paper, we prove that in the sparse regime, the ASPCA algorithm also attains the minimax rate. All these sparse setting results currently require the additional condition of consistency of DT—without this condition, the rate optimality question remains open.

Finally, our analysis leaves some open questions in the intermediate thin regime. According to Theorem 3.1, the lower bound in this regime is smaller by a factor of (log N)^1−q/2, as compared to the sparse setting. Therefore, whether there exists an estimator (and in particular, one with low complexity), that attains the current lower bound, or whether this lower bound can be improved is an open question for future research. However, as we indicated at the end of Section 3, the eigenvector being thin but not sparse is a somewhat rare occurrence in terms of mathematical possibilities.

APPENDIX A: PROOFS

A.1. Asymptotic risk of the standard PCA estimator

To prove Theorem 2.1, on the risk of the PCA estimator, we use the following lemmas. Throughout, ‖B‖ = sup{x^T Bx : ‖x‖₂ = 1} denotes the spectral norm on square matrices.

Deviation of extreme Wishart eigenvalues and quadratic forms

In our analysis, we will need a probabilistic bound for deviations of ‖n⁻¹ZZ^T − I‖. This is given in the following lemma, proven in Appendix B.

Lemma A.1. Let Z be an N × n matrix with i.i.d. N (0, 1) entries. Suppose N < n and set $t_n=8\sqrt{n^{-1}\text{log}n}$ and γ_n = N/n. Then for any c > 0, there exists n_c ≥ 1 such that for all n ≥ n_c,

$$\mathbb{P}(\Vert n^{-1}{\mathbf{\text{ZZ}}}^T-I_N\Vert >{\gamma }_n+2\sqrt{{\gamma }_n}+c{t}_n)\le 2n^{-c^2}.$$ (A.1)

Lemma A.2 [Johnstone (2001)]. Let ${\chi }_n^2$ denote a Chi-square random variable with n degrees of freedom. Then

$$\mathbb{P}({\chi }_n^2>n(1+\epsilon ))\le e^{-3n{\epsilon }^2/16}(0<\epsilon <\frac{1}{2}),$$ (A.2)

$$\mathbb{P}({\chi }_n^2<n(1-\epsilon ))\le e^{-n{\epsilon }^2/4}(0<\epsilon <1),$$ (A.3)

$$\mathbb{P}({\chi }_n^2>n(1+\epsilon ))\le \frac{\sqrt{2}}{\epsilon \sqrt{n}}{e}^{-n{\epsilon }^2/4}(0<\epsilon <1/2,n\ge 16).$$ (A.4)

Lemma A.3 [Johnstone and Lu (2009)]. Let y_1i, y_2i, i = 1, … , n, be two sequences of mutually independent, i.i.d. N(0, 1) random variables. Then for large n and any b s.t. 0 < b ≪ $\sqrt{n}$,

$$\mathbb{P}(|\frac{1}{n}\sum _{i=1}^n{y}_{1i}{y}_{2i}|>\sqrt{b/n})\le 2\text{exp}\{-\frac{3b}{2}+O(n^{-1}{b}^2)\}.$$ (A.5)

Perturbation of eigen-structure

The following lemma, modified in Appendix B from Paul (2005), is convenient for risk analysis of estimators of eigenvectors. Several variants of this lemma appear in the literature, most based on the approach of Kato (1980). To state it, let the eigenvalues of a symmetric matrix A be denoted by λ₁(A) ≥ ⋯ ≥ λ_m (A), with the convention that λ₀(A) = ∞ and λ_m+1 (A) = −∞. Let P_s denote the projection matrix onto the possibly multidimensional eigenspace corresponding to λ_s (A) and define

$$H_r(A)=\sum _{s\ne r}\frac{1}{{\mathrm{\lambda }}_s(A)-{\mathrm{\lambda }}_r(A)}{P}_s(A).$$

Note that H_r (A) may be viewed as the resolvent of A “evaluated at λ_r (A).”

Lemma A.4. Let A and B be symmetric m × m matrices. Suppose that λ_r (A) is a unique eigenvalue of A with

$${\delta }_r(A)=\text{min}\{|{\mathrm{\lambda }}_j(A)-{\mathrm{\lambda }}_r(A)|:1\le j\ne r\le m\}.$$

Let p_r denote the unit eigenvector associated with the λ_r(A). Then

$${\mathbf{p}}_r(A+B)⊝{\mathbf{p}}_r(A)=-H_r(A)B{\mathbf{p}}_r(A)+R_r,$$ (A.6)

where, if $4\Vert B\Vert \le {\delta }_r^{-1}$ (A),

$$\Vert R_r\Vert \le K{\delta }_r^{-1}(A)\Vert H_r(A)B{\mathbf{p}}_r(A)\Vert \Vert B\Vert ,$$ (A.7)

and we may take K = 30.

Proof of Theorem 2.1. First we out line the approach. For notational simplicity, throughout this subsection, we write θ̂_ν to mean θ̂_ν,PCA. Recall that the loss function L(θ̂_ν, θ_ν) = ‖θ̂_ν ⊝ θ_ν‖². Invoking Lemma A.4 with A = ∑ and B = S − ∑ we get

$${\widehat{\theta }}_{\nu }⊝{\theta }_{\nu }=-H_{\nu }\mathbf{S}{\theta }_{\nu }+R_{\nu },$$ (A.8)

where and

$$H_{\nu }\equiv H_{\nu }(\sum )≔\sum _{1\le \mu \ne \nu \le M}\frac{1}{{\mathrm{\lambda }}_{\mu }-{\mathrm{\lambda }}_{\nu }}{\theta }_{\mu }{\theta }_{\mu }^T-\frac{1}{{\mathrm{\lambda }}_{\nu }}{P}_{\perp }$$ (A.9)

and $P_{\perp }=I-{\sum }_{\mu =1}^M{\theta }_{\mu }{\theta }_{\mu }^T$. Note that H_νθ_ν = 0 and that H_ν∑θ_ν = 0.

Let ${\epsilon }_{n\nu }=K{\delta }_r^{-1}(\sum )\Vert \mathbf{S}-\sum \Vert$. We have from (A.7) that

$$\Vert R_{\nu }\Vert \le \Vert H_{\nu }\mathbf{S}{\theta }_{\nu }\Vert {\delta }_{n\nu }^{\prime },$$

and we will show that as n → ∞, ε_nν → 0 with probability approaching 1 and that

$$\Vert H_{\nu }\mathbf{S}{\theta }_{\nu }{\Vert }^2{(1-{\epsilon }_{n\nu })}^2\le L({\widehat{\theta }}_{\nu },{\theta }_{\nu })\le \Vert H_{\nu }\mathbf{S}{\theta }_{\nu }{\Vert }^2{(1+{\epsilon }_{n\nu })}^2.$$ (A.10)

Theorem 2.1 then follows from an (exact, nonasymptotic) evaluation,

$$𝔼[{\Vert H_{\nu }\mathbf{S}{\theta }_{\nu }\Vert }^2]=\frac{N-M}{nh({\mathrm{\lambda }}_{\nu })}+\frac{1}{n}\sum _{\mu \ne \nu }\frac{(1+{\mathrm{\lambda }}_{\mu })(1+{\mathrm{\lambda }}_{\nu })}{{({\mathrm{\lambda }}_{\mu }-{\mathrm{\lambda }}_{\nu })}^2}.$$ (A.11)

We begin with the evaluation of (A.11). First we derive a convenient representation of H_νSθ_ν. In matrix form, model (2.2) becomes

$$\mathbf{X}=\sum _{\nu =1}^M\sqrt{{\mathrm{\lambda }}_{\nu }}{\theta }_{\nu }{\upsilon }_{\nu }^T+\mathbf{Z},$$ (A.12)

where ${\upsilon }_{\nu }={({\upsilon }_{\nu i})}_{i=1}^n$, for ν = 1, … , M. Also, define

$$z_{\nu }={\mathbf{Z}}^T{\theta }_{\nu },w_{\nu }={\mathbf{X}}^T{\theta }_{\nu }=\sqrt{{\mathrm{\lambda }}_{\nu }}{\upsilon }_{\nu }+z_{\nu }$$ (A.13)

and

$${\langle \mathbf{a},\mathbf{b}\rangle }_n=\frac{1}{n}\sum _{i=1}^n{a}_i{b}_i\text{\hspace{1em} for arbitrary}\mathbf{a},\mathbf{b}\in {ℝ}^n.$$ (A.14)

Then we have

$$\mathbf{S}{\theta }_{\nu }=\frac{1}{n}\mathbf{X}{w}_{\nu }=\sum _{\mu =1}^M\sqrt{{\mathrm{\lambda }}_{\mu }}{\langle {\upsilon }_{\mu },w_{\nu }\rangle }_n{\theta }_{\mu }+\frac{1}{n}\mathbf{Z}{w}_{\nu }.$$

Using (A.13),

$$\frac{1}{n}{H}_{\nu }\mathbf{Z}{w}_{\nu }=\sum _{\mu \ne \nu }\frac{\langle z_{\mu },w_{\nu }\rangle }{{\mathrm{\lambda }}_{\mu }-{\mathrm{\lambda }}_{\nu }}{\theta }_{\mu }-\frac{1}{n{\mathrm{\lambda }}_{\nu }}{P}_{\perp }\mathbf{Z}{w}_{\nu }.$$

Using (A.9), H_νθ_μ = (λ_μ − λ_ν)⁻¹ θ_μ for μ ≠ ν, and we arrive at the desired representation

$$H_{\nu }\mathbf{S}{\theta }_{\nu }=\sum _{\mu \ne \nu }\frac{{\langle w_{\mu },w_{\nu }\rangle }_n}{{\mathrm{\lambda }}_{\mu }-{\mathrm{\lambda }}_{\nu }}{\theta }_{\mu }-\frac{1}{n{\mathrm{\lambda }}_{\nu }}{P}_{\perp }\mathbf{Z}{w}_{\nu }.$$ (A.15)

By orthogonality,

$${\Vert H_{\nu }\mathbf{S}{\theta }_{\nu }\Vert }^2=\sum _{\mu \ne \nu }\frac{{\langle w_{\mu },w_{\nu }\rangle }_n^2}{{({\mathrm{\lambda }}_{\mu }-{\mathrm{\lambda }}_{\nu })}^2}+\frac{1}{n^2{\mathrm{\lambda }}_{\nu }^2}{w}_{\nu }^T{\mathbf{Z}}^T{P}_{\perp }\mathbf{Z}{w}_{\nu }.$$ (A.16)

Now we compute the expectation. One verifies that z_ν ~ N(0, I_n) independently of each other and of each υ_ν ~ N(0, I_n), so that w_ν ~ N (0, (1 + λ_ν) I_n) independently. Hence, for μ ≠ ν,

$$𝔼[{\langle w_{\mu },w_{\nu }\rangle }_n^2=n^{-2}𝔼\text{tr}(w_{\nu }{w}_{\nu }^T{w}_{\mu }{w}_{\mu }^T)=n^{-2}\text{tr}((1+{\mathrm{\lambda }}_{\mu })(1+{\mathrm{\lambda }}_{\nu })I_n)=n^{-1}(1+{\mathrm{\lambda }}_{\mu })(1+{\mathrm{\lambda }}_{\nu }).$$ (A.17)

From (A.13),

$$𝔼[w_{\nu }^T{\mathbf{Z}}^T{P}_{\perp }\mathbf{Z}{w}_{\nu }|\mathbf{Z}]=z_{\nu }^T{\mathbf{Z}}^T{P}_{\perp }\mathbf{Z}{z}_{\nu }+{\mathrm{\lambda }}_{\nu }𝔼[{\upsilon }_{\nu }^T{\mathbf{Z}}^T{P}_{\perp }\mathbf{Z}{\upsilon }_{\nu }|\mathbf{Z}]=\text{tr}(\mathbf{Z}{\mathbf{Z}}^T{P}_{\perp }\mathbf{Z}{\mathbf{Z}}^T{\theta }_{\nu }{\theta }_{\nu }^T)+{\mathrm{\lambda }}_{\nu }\text{tr}(P_{\perp }\mathbf{Z}{\mathbf{Z}}^T).$$

Now, it can be easily verified that if W ≔ ZZ^T ~ W_N(n, I), then for arbitrary symmetric N × N matrices Q, R, we have

$$𝔼[\text{tr}(WQWR)]=n[\text{tr}(QR)+\text{tr}(Q)\text{tr}(R)]+n^2\text{tr}(QR).$$ (A.18)

Taking Q = P_⊥ and $R={\theta }_{\mu }{\theta }_{\mu }^T$ and noting that QR = 0, by (A.18) we have

$$𝔼[w_{\nu }^T{\mathbf{Z}}^T{P}_{\perp }\mathbf{Z}{w}_{\nu }]=n\text{tr}(P_{\perp })+n{\mathrm{\lambda }}_{\nu }\text{tr}(P_{\perp })=n(N-M)(1+{\mathrm{\lambda }}_{\nu }).$$ (A.19)

Combining (A.17) with (A.19) in computing the expectation of (A.16), we obtain the expression (A.11) for 𝔼‖H_νSθ_ν‖².

A.2. Bound for ‖S − ∑‖

We begin with the decomposition of the sample covariance matrix S. Introduce the abbreviation ξ_μ = n⁻¹Zυ_μ. Then

$$\mathbf{S}=\sum _{\mu ,\mu \prime =1}^M\sqrt{{\mathrm{\lambda }}_{\mu }{\mathrm{\lambda }}_{\mu \prime }}{\langle {\upsilon }_{\mu },{\upsilon }_{\mu \prime }\rangle }_n{\theta }_{\mu }{\theta }_{\mu \prime }^T+\sum _{\mu =1}^M\sqrt{{\mathrm{\lambda }}_{\mu }}({\theta }_{\mu }{\xi }_{\mu }^T+{\xi }_{\mu }{\theta }_{\mu }^T)+n^{-1}\mathbf{Z}{\mathbf{Z}}^T$$ (A.20)

and from (2.1), with V_μμ′= |〈υ_μ, υ_μ′〉_n − δ_μμ′| and δ_μμ′ denoting the Kronecker symbol,

$$\Vert \mathbf{S}-\sum \Vert \le \sum _{\mu ,\mu \prime =1}^M\sqrt{{\mathrm{\lambda }}_{\mu }{\mathrm{\lambda }}_{\mu \prime }}{V}_{\mu \mu \prime }+2\sum _{\mu =1}^M\sqrt{{\mathrm{\lambda }}_{\mu }}\Vert {\xi }_{\mu }\Vert +\Vert n^{-1}\mathbf{Z}{\mathbf{Z}}^T-I\Vert .$$ (A.21)

We establish a bound for ‖S − ∑‖ with probability converging to one. Introduce notation

$${\eta }_n=\sqrt{N^{-1}\text{log}n},{\overline{\eta }}_n=\sqrt{n^{-1}\text{log}n},{\gamma }_n=N/n,\sqrt{\mathrm{\Lambda }}=\sum _{\mu =1}^M\sqrt{{\mathrm{\lambda }}_{\mu }}.$$

Fix c > 0 and assume that γ_n ≤ 1. Initially, we assume that 2cη_n ≤ 1/2, which is equivalent to N ≥ 16c² log n.

We introduce some events of high probability under which (A.21) may be bounded. Thus, let D₁ be the intersection of the events

$$|\Vert {\upsilon }_{\mu }{\Vert }_n^2-1|\le 2c{\overline{\eta }}_n,1\le \mu \le M,|{\langle {\upsilon }_{\mu },{\upsilon }_{\mu \prime }\rangle }_n|c{\overline{\eta }}_n,1\le \mu \ne \mu \prime \le M,N^{-1}\Vert \mathbf{Z}{\upsilon }_{\mu }{\Vert }^2/\Vert {\upsilon }_{\mu }{\Vert }^2\le 1+2c{\eta }_n,1\le \mu \le M,$$ (A.22)

and let D₂ be the event

$$\Vert n^{-1}\mathbf{Z}{\mathbf{Z}}^T-I\Vert \le {\gamma }_n+2\sqrt{{\gamma }_n}+8c{\overline{\eta }}_n.$$ (A.23)

To bound the probability of $D_1^c$, in the case of the first line of (A.22), use (A.3) and (A.4) with ε = 2cη̄_n. For the second, use (A.5) with b = c² log n. For the third, observe that Zυ_μ/‖υ_μ‖ ~ N_N(0, I), and again use (A.4), this time with ε = 2cη_n < 1/2. For $D_2^c$, we appeal to Lemma A.1. As a result,

$$\mathbb{P}(D_1^c)\le 3M{n}^{-c^2}+M(M-1)n^{-(3/2)c^2+O(n^{-1}{\text{log}}^{2}n)},\mathbb{P}(D_2^c)\le 2n^{-c^2}.$$ (A.24)

To bound (A.21) on the event D₁ ∩ D₂, we use bounds (A.22) and (A.23), and also write

$$\Vert {\xi }_{\mu }\Vert =\sqrt{{\gamma }_n}\frac{\Vert \mathbf{Z}{\upsilon }_{\mu }\Vert }{\sqrt{N}\Vert {\upsilon }_{\mu }\Vert }\frac{\Vert {\upsilon }_{\mu }\Vert }{\sqrt{n}}\le \sqrt{{\gamma }_n}{(1+2c{\eta }_n)}^{1/2}{(1+2c{\overline{\eta }}_n)}^{1/2}=\sqrt{{\gamma }_n}{H}_n,$$ (A.25)

say, and also noting that η̄_n ≤ η_n, we obtain

$$\Vert \mathbf{S}-\sum \Vert \le \sqrt{{\gamma }_n}[2c{\eta }_n\mathrm{\Lambda }+2\sqrt{\mathrm{\Lambda }}{H}_n+4(1+2c{\eta }_n)].$$ (A.26)

Now combine the bound 2cη_n < 1/2 with H_n ≤ 3/2 and $2\sqrt{\mathrm{\Lambda }}\le \mathrm{\Lambda }+1$ to conclude that on D₁ ∩ D₂,

$$\Vert \mathbf{S}-\sum \Vert \le 2(\mathrm{\Lambda }+4)\sqrt{{\gamma }_n}$$

and so

$${\epsilon }_{n\nu }\le 2K{\delta }_{\nu }^{-1}(\sum )(\mathrm{\Lambda }+4)\sqrt{{\gamma }_n}\to 0$$

since N/n → 0.

Let us now turn to the case N ≤ 16c² log n. We can replace the last event in (A.22) by the event

$$N^{-1}{\Vert \mathbf{Z}{\upsilon }_{\mu }\Vert }^2/{\Vert {\upsilon }_{\mu }\Vert }^2\le 2(c^2\text{log}n+\text{log}N),1\le \mu \le M,$$

and the second bound holds for $\mathbb{P}(D_1^c)$ for sufficiently large n, using the bound $\mathbb{P}(N^{-1}{\chi }_N^2>a)\le 2N(1-\Phi (\sqrt{a}))\le N\sqrt{2/a\pi }{e}^{-a/2}$ for any a > 0. In (A.25), we replace the term (1 + 2cη_n)^1/2 by (2c² log n + 2 log N)^1/2 which may be bounded by $a_1\sqrt{\text{log}n}$. As soon as N ≥ 4c², we also have $2c{\eta }_n\le \sqrt{\text{log}n}$ and so $1+2c{\overline{\eta }}_n\le 1+\sqrt{{\gamma }_n\text{log}n}$. This leads to a bound for the analog of H_n in (A.26) and so to

$$\Vert \mathbf{S}-\sum \Vert \le \sqrt{{\gamma }_n\text{log}n}\{\mathrm{\Lambda }+2a_1\sqrt{\mathrm{\Lambda }}{(1+\sqrt{{\gamma }_n\text{log}n)}}^{1/2}+a_2\}.$$

When N ≤ 16c² log n, we have $\sqrt{{\gamma }_n\text{log}n}\le 4c\text{log}n/\sqrt{n}$ and so

$${\epsilon }_{n\nu }\le a_{3}K{\delta }_{\nu }^{-1}(\sum )(\mathrm{\Lambda }+1)\text{log}n/\sqrt{n}\to 0.$$

To summarize, choose $c=\sqrt{2}$, say, so that D_n = D₁ ∩ D₂ has probability at least 1−O(n⁻²), and on D_n we have ε_nν → 0. This completes the proof of (A.10).

Theorem 2.1 now follows from noticing that L(θ̂_ν, θ_ν) ≤ 2 and so

$$𝔼[L({\widehat{\theta }}_{\nu },{\theta }_{\nu }),D_n^c]\le 2\mathbb{P}(D_n^c)=O(n^{-2})=o(𝔼\Vert H_{\nu }\mathbf{S}{\theta }_{\nu }{\Vert }^2)$$

and an additional computation using (A.16) which shows that

$$𝔼[{\Vert H_{\nu }\mathbf{S}{\theta }_{\nu }\Vert }^2,D_n^c]\le {(𝔼[\Vert H_{\nu }\mathbf{S}{\theta }_{\nu }{\Vert }^4])}^{1/2}P(D_n^c)=o(𝔼\Vert H_{\nu }\mathbf{S}{\theta }_{\nu }{\Vert }^2).$$

A.3. Lower bound on the minimax risk

In this subsection, we prove Theorems 3.1 and 3.2. The key idea in the proofs is to utilize the geometry of the parameter space in order to construct appropriate finite-dimensional subproblems for which bounds are easier to obtain. We first give an overview of the general machinery used in the proof.

Risk bounding strategy

A key tool for deriving lower bounds on the minimax risk is Fano’s lemma. In this subsection, we use superscripts on vectors θ as indices, not exponents. First, we fix ν ∈ {1, … , M} and then construct a large finite subset ℱ of ${\mathrm{\Theta }}_q^M$ (C₁, … , C_M), such that for some δ > 0, to be chosen

$${\mathit{\theta }}^1,{\mathit{\theta }}^2\in ℱ\Rightarrow L({\theta }_{\nu }^1,{\theta }_{\nu }^2)\ge 4\delta .$$

This property will be referred to as “4δ-distinguishability in θ_ν.” Given any estimator θ̄ of θ, based on data X_n = (X₁, … , X_n), define a new estimator ϕ(X_n) = θ*, whose M components are given by ${\theta }_{\mu }^{*}={\text{arg min}}_{\mathit{\theta }\in ℱ}L({\widehat{\theta }}_{\mu },{\theta }_{\mu })$, where θ̂_μ is the μth column of θ̂. Then, by Chebyshev’s inequality and the 4δ-distinguishability in θ_ν, it follows that

$$\underset{\mathit{\theta }\in {\mathrm{\Theta }}_q^M(C_1,\dots ,C_M)}{\text{sup}}{𝔼}_{\mathit{\theta }}L({\widehat{\theta }}_{\nu },{\theta }_{\nu })\ge \delta \underset{\mathit{\theta }\in ℱ}{\text{sup}}{\mathbb{P}}_{\mathit{\theta }}(\varphi ({\mathbf{X}}_n)\ne \mathit{\theta }).$$ (A.27)

The task is then to find an appropriate lower bound for the quantity on the right-hand side of (A.27). For this, we use the following version of Fano’s lemma, due to Birgé (2001), modifying a result of Yang and Barron (1999), pages 1570 and 1571.

Lemma A.5. Let {P_θ : θ ∈ Θ} be a family of probability distributions on a common measurable space, where Θ is an arbitrary parameter set. Let p_max be the minimax risk over Θ, with the loss function L′(θ, θ′) = 1θ≠θ′,

$$p_{\text{max}}=\underset{T}{\text{inf}}\underset{\theta \in \mathrm{\Theta }}{\text{sup}}{\mathbb{P}}_{\theta }(T\ne \theta )=\underset{T}{\text{inf}}\underset{\theta \in \mathrm{\Theta }}{\text{sup}}𝔼L\prime (\theta ,T),$$

where T denotes an arbitrary estimator of θ with values in Θ. Then for any finite subset ℱ of Θ, with elements θ₁, … ,θ_J where J = |ℱ |,

$$p_{\text{max}}\ge 1-\underset{Q}{\text{inf}}\frac{J^{-1}{\sum }_{i=1}^{J}K(P_i,Q)+\text{log}2}{\text{log}J},$$ (A.28)

where P_i = ℙ_θi, and Q is an arbitrary probability distribution, and K(P_i,Q) is the Kullback–Leibler divergence of Q from P_i.

The following lemma, proven in Appendix B, gives the Kullback–Leibler discrepancy corresponding to two different values of the parameter.

Lemma A.6. Let ${\mathit{\theta }}^j≔[{\theta }_1^j:\dots :{\theta }_M^j],j=1,2$ be two parameters (i.e., for each j, ${\theta }_k^j’s$ are orthonormal). Let ∑_j denote the matrix given by (2.1) with θ = θ^j (and σ = 1). Let P_j denote the joint probability distribution of n i.i.d. observations from N (0, ∑_j) and let η(λ) = λ/(1 + λ). Then the Kullback–Leibler discrepancy of P₂ with respect to P₁ is given by

$${{\rm K}}_{1,2}≔\mathit{K}({\mathit{\theta }}^1,{\mathit{\theta }}^2)=\frac{n}{2}[\sum _{\mu =1}^M\eta ({\mathrm{\lambda }}_{\mu }){\mathrm{\lambda }}_{\mu }-\sum _{\mu =1}^M\sum _{\mu \prime =1}^M\eta ({\mathrm{\lambda }}_{\mu }){\mathrm{\lambda }}_{\mu \prime }{\langle {\theta }_{\mu \prime }^1,{\theta }_{\mu }^2\rangle }^2].$$ (A.29)

.

Geometry of the hypothesis set and sphere packing

Next, we describe the construction of a large set of hypotheses ℱ, satisfying the 4δ distinguishability condition. Our construction is based on the well-studied sphere-packing problem, namely how many unit vectors can be packed onto 𝕊^m−1 with given minimal pairwise distance between any two vectors.

Here we follow the construction due to Zong (1999) (page 77). Let m be a large positive integer, and m₀ = ⌊2m/9⌋. Define $Y_m^{*}$ as the maximal set of points of the form z = (z₁, … , z_m) in 𝕊^m−1 such that the following is true:

$$\sqrt{m_0}{z}_i\in \{-1,0,1\}\forall i\sum _{i=1}^m|z_i|\le \sqrt{m_0}$$

and

$$\text{for}\mathbf{z},\mathbf{z}\prime \in Y_m^{*}\Vert \mathbf{z}-\mathbf{z}\prime \Vert \ge 1.$$

For any m ≥ 1, the maximal number of points lying on 𝕊^m−1 such that any two points are at distance at least 1, is called the kissing number of an m-sphere. Zong (1999) used the construction described above to derive a lower bound on the kissing number, by showing that $|Y_m^{*}|\ge {(9/8)}^{m(1+o(1))}$ for m large.

Next, for m < N − M we use the sets $Y_m^{*}$ to construct our hypothesis set ℱ of the same size, $|ℱ|=|Y_m^{*}|$. To this end, let ${\{{\mathbf{e}}_{\mu }\}}_{\mu =1}^N$ denote the standard basis of ℝ^N. Our initial set θ⁰ is composed of the first M standard basis vectors, θ⁰ = [e₁: … :e_M]. Then, for fixed ν, and values of m, r yet to be determined, each of the other hypotheses θ^j ∈ ℱ has the same vectors as θ⁰ for k ≠ ν. The difference is that the νth vector is instead given by

$${\theta }_{\nu }^j=\sqrt{1-r^2{\mathbf{e}}_{\nu }}+r\sum _{l=1}^m{z}_l^j{\mathbf{e}}_{M+l},j=1,\dots ,|F|,$$ (A.30)

where ${\mathbf{z}}^j=(z_1^j,\dots ,z_m^j),j\ge 1$, is an enumeration of the elements of $Y_m^{*}$. Thus ${\theta }_{\nu }^j$ perturbs e_ν in subsets of the fixed set of coordinates {M + 1, … , M + m}, according to the sphere-packing construction for 𝕊^m−1.

The construction ensures that ${\theta }_1^j,\dots ,{\theta }_M^j$ are orthonormal for each j. In particular, $\langle {\theta }_{\mu }^j,{\mathbf{e}}_{\mu \prime }\rangle$, vanishes unless μ = μ′, and so (A.29) simplifies to

$$K({\mathit{\theta }}^j,{\mathit{\theta }}^0)=\frac{1}{2}nh({\mathrm{\lambda }}_{\nu })(1-{\langle {\theta }_{\nu }^j,{\theta }_{\nu }^0\rangle }^2)=\frac{1}{2}nh({\mathrm{\lambda }}_{\nu })r^2$$ (A.31)

for j = 1, … , |ℱ |. Finally, $\langle {\theta }_{\nu }^j,{\theta }_{\nu }^k\rangle =1-r^2+r^2\langle {\mathbf{z}}^j,{\mathbf{z}}^k\rangle$, and so by construction, for any θ^j, θ^k ∈ ℱ with j ≠ k, we have

$$L({\theta }_{\nu }^j,{\theta }_{\nu }^k)\ge r^2.$$ (A.32)

In other words, the set ℱ is r²-distinguishable in θ_ν. Consequently, combining (A.27), (A.28) and (A.31) (taking Q = P_θ⁰ in Lemma A.5), we have

$$R_{\nu }^{*}=\underset{{\widehat{\theta }}_{\nu }}{\text{inf}}\underset{{\mathrm{\Theta }}_q(\mathbf{C})}{\text{sup}}𝔼L({\widehat{\theta }}_{\nu },{\theta }_{\nu })\ge (r^2/4)[1-a(r,ℱ)]$$ (A.33)

with

$$a(r,ℱ)=\frac{nh({\mathrm{\lambda }}_{\nu })r^2/2+\text{log}2}{\text{log}|ℱ|}.$$ (A.34)

Proof of Theorem 3.1. It remains to specify m and let r ∈ (0, 1). Let $Y_m^{*}$ be the sphere-packing set defined above, and let ℱ be the corresponding set of hypotheses, defined via (A.30).

Let c₁ = log(9/8), then we have log |ℱ | ≥ b_mc₁m, where b_m → 1 as m → ∞. Now choose r = r(m) so that a(r, ℱ) ≤ 3/4 asymptotically in the bound (A.33). To accomplish this, set

$$r^2=\frac{c_{1}m}{nh({\mathrm{\lambda }}_{\nu })}.$$ (A.35)

Indeed, inserting this into (A.34) we find that

$$a(r,ℱ)\le \frac{c_{1}m/2+\text{log}2}{b_m{c}_{1}m}.$$

Therefore, so long as m ≥ m_*, an absolute constant, we have a(r, ℱ₀) ≤ 3/4 and hence $R_{\nu }^{*}\ge r^2/16=(c_1/16)m{\tau }_{\nu }^2.$.

We also need to ensure that ${\theta }_{\nu }^j\in {\mathrm{\Theta }}_q(C_{\nu })$. Since exactly m₀ coordinates are nonzero out of {M + 1, … , M + m},

$$\Vert {\theta }_{\nu }^j{\Vert }_q^q={(1-r^2)}^{q/2}+r^q{m}_0^{1-q/2}\le 1+a_q{r}^q{m}^{1-q/2},$$

, where a_q = (2/9)^1−q/2. A sufficient condition for ${\theta }_{\nu }^{(j)}\in {\mathrm{\Theta }}_q(C_{\nu })$ is that

$$a_{q}m{(r^2/m)}^{q/2}\le {\overline{C}}_{\nu }^q.$$ (A.36)

Our choice (A.35) fixes r²/m, and so, recalling that $A_q=1/(a_q{c}_1^{q/2})$, the previous display becomes

$$m\le A_q{\overline{C}}_{\nu }^q{[nh({\mathrm{\lambda }}_{\nu })]}^{q/2}.$$

To simultaneously ensure that (i) r² < 1, (ii) m does not exceed the number of available co-ordinates, N − M and (iii) ${\theta }_{\nu }^j\in {\mathrm{\Theta }}_q(C_{\nu })$, we set

$$m=\lfloor m\prime \rfloor ,m\prime =\text{min}\{nh({\mathrm{\lambda }}_{\nu }),N-M,A_q{\overline{C}}_{\nu }^q{(nh({\mathrm{\lambda }}_{\nu }))}^{q/2}\}.$$

Recalling (3.1), (3.2) and (3.3), we have

$$m\prime =\text{min}\{{\tau }_{\nu }^{-2},N\prime ,m_{\nu }\}={\tau }_{\nu }^{-2}\text{min}\{1,{\tau }_{\nu }^2·\text{min}\{N\prime ,m_{\nu }\}\}.$$

To complete the proof of Theorem 3.1, set B₁ = [(m_* + 1)/m_*]c₁/16 and observe that

$$R_{\nu }^{*}\ge B_{1}m\prime {\tau }_{\nu }^2.$$

Proof of Theorem 3.2. The construction of the set of hypotheses in the proof of Theorem 3.1 considered a fixed set of potential nonzero coordinates, namely {M + 1, … ,M + m}. However, in the sparse setting, when the effective dimension is significantly smaller than the nominal dimension N, it is possible to construct a much larger collection of hypotheses by allowing the set of nonzero coordinates to span all remaining coordinates {M + 1, … , N}.

In the proof of Theorem 3.2 we shall use the following lemma, proven in Appendix B. Call A ⊂ {1, … , N} an m-set if |A| = m.

Lemma A.7. Let k be fixed, and let 𝒜_k be the maximal collection of m-sets such that the intersection of any two members has cardinality at most k −1. Then, necessarily,

$$|{𝒜}_k|\ge \left(\begin{array}{c}N\hfill \\ k\hfill \end{array}\right)/{\left(\begin{array}{c}m\hfill \\ k\hfill \end{array}\right)}^2.$$ (A.37)

Let k = [m₀/2] + 1 and m₀ = [βm] with 0 < β < 1. Suppose that m, N → ∞with m = o(N). Then

$$|{𝒜}_k|\ge \text{exp}[N\epsilon (\beta m/2N)-2m\epsilon (\beta /2)](1+o(1)),$$ (A.38)

, where ε(x) is the Shannon entropy function,

$$\epsilon (x)=-x\text{log}(x)-(1-x)\text{log}(1-x),0<x<1.$$

Let π be an m-set contained in {M + 1, … , N}, and construct a family ℱ_π by modifying (A.30) to use the set π rather than the fixed set {M +1, … , M + m} as in Theorem 3.1,

$${\theta }_{\nu }^{(j,\pi )}=\sqrt{1-r^2{\mathbf{e}}_{\nu }}+r\sum _{l\in \pi }{z}_l^j{\mathbf{e}}_l,j=1,\dots ,|Y_m^{*}|.$$

We will choose m below to ensure that ${\theta }_{\nu }^{(j,\pi )}\in {\mathrm{\Theta }}_q(C_{\nu })$. Let 𝒫 be a collection of sets π such that, for any two sets π and π′ in 𝒫, the set π ∩ π′ has cardinality at most m₀/2. This ensures that the sets ℱ_π are disjoint for π ≠ π′, since each ${\theta }_{\nu }^{(j,\pi )}$ is nonzero in exactly m₀ + 1 coordinates. This construction also ensures that

$$\text{for all}{\mathit{\theta }}^1,{\mathit{\theta }}^2\in \underset{\pi \in 𝒫}{\cup }{ℱ}_{\pi }L({\mathit{\theta }}^1,{\mathit{\theta }}^2)\ge (\frac{m_0}{2}+\frac{m_0}{2}){\left(\frac{r}{\sqrt{m_0}}\right)}^2=r^2.$$

Define ℱ ≔ ∪_π∈𝒫 ℱ_π. Then

$$|ℱ|=\left|\underset{\pi \in 𝒫}{\cup }{ℱ}_{\pi }\right|=|𝒫||Y_m^{*}|\ge |𝒫|{(9/8)}^{m(1+o(1))}.$$ (A.39)

By Lemma A.7, there is a collection 𝒫 such that |𝒫| is at least exp([Nε(m/9N)− 2mε(1/9)](1 + o(1))). Since ε(x) ≥ − x log x, it follows from (A.39) that

$$\frac{\text{log}|ℱ|}{m}\ge (\frac{1}{9}\text{log}\frac{9N}{m}-2\epsilon (1/9))+\text{log}(9/8)(1+o(1))\ge \frac{\alpha }{9}\text{log}N+O(1),$$

since m = O (N^1−α).

Proceeding as for Theorem 3.1, we have log |ℱ| ≥ b_m (α/9)m log N, where b_m → 1. Let us set (with m still to be specified)

$$r^2=m\frac{(\alpha /9)\text{log}N}{nh({\mathrm{\lambda }}_{\nu })}=m{\overline{\tau }}_{\nu }^2.$$ (A.40)

Again, so long as m ≥ m_*, we have a(r, ℱ) ≤ 3/4 and $R_{\nu }^{*}\ge r^2/16=(1/16)m{\overline{\tau }}_{\nu }^2$. We also need to ensure that ${\theta }_{\nu }^{(j,\pi )}\in {\Theta }_q(C_{\nu })$, which as before is implied by (A.36). Substituting (A.40) puts this into the form

$$m\le {\overline{m}}_{\nu }=a_q^{-1}{({\overline{C}}_{\nu }/{\overline{\tau }}_{\nu })}^q.$$

To simultaneously ensure that (i) r² < 1, (ii) m does not exceed the number of available co-ordinates, N − M and (iii) ${\theta }_{\nu }^j\in {\Theta }_q(C_{\nu })$, we set

$$m=\lfloor m\prime \rfloor ,m\prime =\text{min}\{{\overline{\tau }}_{\nu }^{-2},N-M,{\overline{m}}_{\nu }\}.$$

The assumption that ${\overline{C}}_{\nu }^q{n}^{q/2}=O(N^{1-\alpha })$ for some α ∈ (0, 1) is equivalent to the assertion m̄_ν = O(N^1−α), and so for n sufficiently large, m̄_ν ≤ N − M and so m′ = m̄_ν so long as ${\overline{m}}_{\nu }{\overline{\tau }}_{\nu }^2\le 1$. Theorem 3.2 now follows from our bound on $R_{\nu }^{*}$.

A.4. Lower bound on the risk of the DT estimator

To prove Theorem 4.1, assume w.l.o.g. that 〈θ̂_1,DT,θ₁〉 > 0, and decompose the loss as

$$L({\widehat{\theta }}_{1,\text{DT}},{\theta }_1)={\Vert {\theta }_1-{\theta }_{1,I}\Vert }^2+{\Vert {\widehat{\theta }}_{1,\text{DT}}-{\theta }_{1,I}\Vert }^2,$$ (A.41)

where I = I (γ_n) is the set of coordinates selected by the DT scheme and θ_{1, I} denotes the subvector of θ₁ corresponding to this set. Note that, in (A.41), the first term on the right can be viewed as a bias term while the second term can be seen as a variance term.

We choose a particular vector θ₁ = θ_* ∈ Θ_q(C) so that

$$𝔼{\Vert {\theta }_{*}-{\theta }_{*,I}\Vert }^2\ge K{\overline{C}}^q{n}^{-(1-q/2)/2}.$$ (A.42)

This, together with (A.41), proves Theorem 4.1 since the worst case risk is clearly at least as large as (A.42). Accordingly, set r_n = C̄^q/2n^{−(1−q/2)/4}, where C̄^q = C^q −1. Since C^qn^q/4 = o(n^1/2), we have r_n = o(1), and so for sufficiently large n, we can take r_n < 1 and define

$${\theta }_{*,k}=\{\begin{array}{cc}\sqrt{1-r_n^2,}\hfill & \text{if}k=1,\hfill \\ \frac{r_n}{\sqrt{m_n}},\hfill & \text{if}2\le k\le m_n+1,\hfill \\ 0\hfill & \text{if}{m}_n+2\le k\le N,\hfill \end{array}$$

where m_n = ⌊(1/2)C̄^qn^q/4⌋. Then by construction θ_* ∈ Θ_q(C), since

$$\sum _{k=1}^N{|{\theta }_{*,k}|}^q={(1-r_n^2)}^{q/2}+r_n^q{m}_n^{1-q/2}<1+r_n^q{m}_n^{1-q/2}\le 1+\frac{{\overline{C}}^q}{2^{1-q/2}}<C^q,$$

where the last inequality is due to q ∈ (0, 2) and C̄^q = C^q −1.

For notational convenience, let ${\alpha }_n=\gamma \sqrt{\text{log}N/n}$. Recall that DT selects all coordinates k for which S_kk > 1 + α_n. Since ${\mathbf{S}}_{kk}~(1+{\mathrm{\lambda }}_1{\theta }_{*,k}^2){\chi }_n^2/n$, coordinate k is not selected with probability

$$p_k=\mathbb{P}({\mathbf{S}}_{kk}<1+{\alpha }_n)=\mathbb{P}({\chi }_n^2<n(1+{\epsilon }_n)),$$ (A.43)

, where ${\epsilon }_n=(1+{\alpha }_n)/(1+{\mathrm{\lambda }}_1{\theta }_{*,k}^2)-1$. Notice that, for k = 2, …, m_n + 1, p_k = p₂ and θ_*,k = 0 for k > m_n + 1. Hence,

$$𝔼{\Vert {\theta }_{*}-{\theta }_{*,I}\Vert }^2=\sum _{k=1}^N{p}_k{|{\theta }_{*,k}|}^2>p_2\sum _{k=2}^{m_n+1}{|{\theta }_{*,k}|}^2=p_2{r}_n^2=p_2{\overline{C}}^q{n}^{-(1-q/2)/2}.$$

Now, use bound (A.3) to show that $n{\epsilon }_n^2\to \infty$ in (A.43) and hence that p₂ → 1. Indeed ${\theta }_{*,2}^2=r_n^2/m_n=2n^{-1/2}(1+o(1))$, and so

$${\epsilon }_n=\frac{{\alpha }_n-{\mathrm{\lambda }}_1{\theta }_{*,k}^2}{1+{\mathrm{\lambda }}_1{\theta }_{*,k}^2}=\frac{1}{2\sqrt{n}}[\gamma \sqrt{\text{log}N}-2{\mathrm{\lambda }}_1]$$

for sufficiently large n. Hence, $n{\epsilon }_n^2\to \infty$, and the proof is complete.

APPENDIX B: PROOFS OF RELEVANT LEMMAS

B.1. Proof of Lemma A.1

We use the following result on extreme eigenvalues of Wishart matrices from Davidson and Szarek (2001).

Lemma B.1. Let Z be a p × q matrix of i.i.d. N (0, 1) entries with p ≤ q. Let s_max (Z) and s_min(Z) denote the largest and the smallest singular value of Z, respectively. Then

$$\mathbb{P}(s_{\text{max}}(Z/\sqrt{q})>1+\sqrt{p/q}+t)\le e^{-q{t}^2/2},$$ (B.1)

$$\mathbb{P}(s_{\text{min}}(Z/\sqrt{q})<1-\sqrt{p/q}+t)\le e^{-q{t}^2/2}.$$ (B.2)

Observe first that

$$\mathrm{\Delta }≔\Vert n^{-1}\mathbf{Z}{\mathbf{Z}}^T-I_N\Vert =\text{max}\{{\mathrm{\lambda }}_1(n^{-1}\mathbf{Z}{\mathbf{Z}}^T)-1,1-{\mathrm{\lambda }}_N(\mathbf{Z}{\mathbf{Z}}^T)\}.$$

Let s_± denote the maximum and minimum singular values of N^−1/2Z. Define $\gamma (t)≔\sqrt{N/n}+t$ for t > 0. Then since $\mathrm{\Delta }=\text{max}\{s_{+}^2-1,1-s_{-}^2\}$, and letting Δ_n(t) ≔ 2γ(t) + γ(t)², we have

$$\{\mathrm{\Delta }>{\mathrm{\Delta }}_n(t)\}\subset \{s_{+}>1+\gamma (t)\}\cup \{s_{-}<1-\gamma (t)\}.$$

We apply Lemma B.1 with p = N and q = n, and get

$$\mathbb{P}(\mathrm{\Delta }>{\mathrm{\Delta }}_n(t))\le 2e^{-n{t}^2/2}.$$

We observe that, with γ_n = N/n ≤ 1,

$${\mathrm{\Delta }}_n(t)=(N/n+2\sqrt{N/n})+t(2+t+2\sqrt{N/n})\le {\gamma }_n+2\sqrt{{\gamma }_n}+t(4+t).$$ (B.3)

Now choose $t=c\sqrt{2\text{log}n/n}$ so that tail probability is at most 2e^−n2t2/2 = 2n^−c2. The result is now proved, since if $c\sqrt{\text{log}n/n}\le 1$, then t (4 + t) ≤ ct_n.

B.2. Proof of Lemma A.4

Paul (2005) introduced the quantities

$${\mathrm{\Delta }}_r≔\frac{1}{2}[\Vert H_r(A)B\Vert +|{\mathrm{\lambda }}_r(A+B)-{\mathrm{\lambda }}_r(A)|\Vert H_r(A)|],$$ (B.4)

,

$${\overline{\mathrm{\Delta }}}_r=\frac{\Vert B\Vert }{{\text{min}}_{1\le j\ne r\le m}|{\mathrm{\lambda }}_j(A)-{\mathrm{\lambda }}_r(A)|}$$ (B.5)

and showed that the residual term R_r can be bounded by

$$\Vert R_r\Vert \le \text{min}\{10{\overline{\mathrm{\Delta }}}_r^2,\Vert H_r(A)B{\mathbf{p}}_r(A)\Vert [\frac{2{\mathrm{\Delta }}_r(1+2{\mathrm{\Delta }}_r)}{1-2{\mathrm{\Delta }}_r(1+2{\mathrm{\Delta }}_r)}+\frac{\Vert H_r(A)B{\mathbf{p}}_r(A)\Vert }{{(1-2{\mathrm{\Delta }}_r(1+2{\mathrm{\Delta }}_r))}^2}\left]\right\},$$ (B.6)

where the second bound holds only if 6r ${\mathrm{\Delta }}_r<(\sqrt{5}-1)/4$.

We now show that if Δ̄_r ≤ 1/4, then we can simplify bound (B.6) to obtain (A.7). To see this, note that |λ_r(A + B) − λ_r(A)| ≤ ‖B‖ and that ‖H_r(A)‖ ≤ [min_j≠r |λ_j (A) − λ_r(A)|]⁻¹, so that

$${\mathrm{\Delta }}_r\le \Vert H_r(A)\Vert \Vert B\Vert \le {\overline{\mathrm{\Delta }}}_r.$$

Now, defining δ ≔ 2 Δ̄_r (1 + 2Δ̄_r) and β ≔ ‖H_r (A)Bp_r (A)‖, we have $10{\overline{\mathrm{\Delta }}}_r^2\le (5/2){\delta }^2$, and the bound (B.6) may be expressed as

$$\Vert R_r|\le \frac{\beta \delta }{1-\delta }\text{min}\{\frac{5}{2}\frac{\delta (1-\delta )}{\beta },1+\frac{\beta }{\delta (1-\delta )}\}.$$

For x > 0, the function x → min{5x/2, 1 + 1/x} ≤ 5/2. Further, if Δ̄_r < 1/4, then δ < 3 Δ̄_r < 3/4, and so we conclude that

$$\Vert R_r\Vert \le 10\beta \delta \le 30\beta {\overline{\mathrm{\Delta }}}_r.$$

B.3. Proof of Lemma A.6

Recall that, if distributions F₁ and F₂ have density functions f₁ and f₂, respectively, such that the support of f₁ is contained in the support of f₂, then the Kullback–Leibler discrepancy of F₂ with respect to F₁, to be denoted by K(F₁, F₂), is given by

$$K(F_1,F_2)=\int \text{log}\frac{f_1(y)}{f_2(y)}{f}_1(y)dy.$$ (B.7)

For n i.i.d. observations X_i, i = 1, … , n, the Kullback–Leibler discrepancy is just n times the Kullback–Leibler discrepancy for a single observation. Therefore, without loss of generality we take n = 1. Since

$${\sum }^{-1}=I-\sum _{\mu =1}^M\eta ({\mathrm{\lambda }}_{\mu }){\theta }_{\mu }{\theta }_{\mu }^T,$$ (B.8)

the log-likelihood function for a single observation is given by

$$\text{log}f(x|\mathit{\theta })=-\frac{N}{2}\text{log}(2\pi )-\frac{1}{2}\text{log}|\sum |-\frac{1}{2}{x}^T{\sum }^{-1}x=-\frac{N}{2}\text{log}(2\pi )-\frac{1}{2}\sum _{\mu =1}^M\text{log}(1+{\mathrm{\lambda }}_{\mu })-\frac{1}{2}(\langle x,x\rangle -\sum _{\mu =1}^M\eta ({\mathrm{\lambda }}_{\mu }){\langle x,{\theta }_{\mu }\rangle }^2).$$ (B.9)

From (B.9), we have

$${{\rm K}}_{1,2}={𝔼}_{{\mathit{\theta }}^1}(\text{log}f(X|{\mathit{\theta }}^1)-\text{log}f(X|{\mathit{\theta }}^2))=\frac{1}{2}\sum _{\mu =1}^M\eta ({\mathrm{\lambda }}_{\mu })[{𝔼}_{{\mathit{\theta }}^1}{(\langle X,{\theta }_{\mu }^1\rangle )}^2-{𝔼}_{{\mathit{\theta }}^1}{(\langle X,{\theta }_{\mu }^2\rangle )}^2]=\frac{1}{2}\sum _{\mu =1}^M\eta ({\mathrm{\lambda }}_{\mu })[\langle {\theta }_{\mu }^1,{\sum }_1{\theta }_{\mu }^1\rangle -\langle {\theta }_{\mu }^2,{\sum }_1{\theta }_{\mu }^2\rangle ]\frac{1}{2}\sum _{\mu =1}^M\eta ({\mathrm{\lambda }}_{\mu })[\sum _{\mu \prime =1}^M{\mathrm{\lambda }}_{\mu \prime }\{{\langle {\theta }_{\mu }^1,{\theta }_{\mu }^1\rangle }^2-{\langle {\theta }_{\mu }^1,{\theta }_{\mu }^2\rangle }^2\}],$$

which equals the RHS of (A.29), since the columns of θ^j are orthonormal for each j = 1, 2.

B.4. Proof of Lemma A.7

Let 𝒫_m be the collection of all m-sets of {1, … , N}, clearly $|{𝒫}_m|=(\begin{array}{c}N\hfill \\ m\hfill \end{array})$. For any m-set A, let ℐ(A) denote the collection of “inadmissible” m-sets A′ for which |A ∩ A′| ≥ k. Clearly

$$|ℐ(A)|\le \left(\begin{array}{c}m\hfill \\ k\hfill \end{array}\right)\left(\begin{array}{c}N-k\hfill \\ m-k\hfill \end{array}\right).$$

If 𝒜_k is maximal, then 𝒫_m = ∪_A∈𝒜k ℐ(A), and so (A.37) follows from the inequality

$$|{𝒫}_m|\le |{𝒜}_k|\underset{A}{\text{max}}|ℐ(A)|$$

and rearrangement of factorials.

Turning to the second part, we recall that Stirling’s formula shows that if k and N → ∞,

$$\left(\begin{array}{c}N\hfill \\ k\hfill \end{array}\right)=\zeta {\left(\frac{N}{2\pi k(N-k)}\right)}^{1/2}\text{exp}\left\{N\epsilon \right(\frac{k}{N}\left)\right\},$$

where ζ ∈ (1 − (6k)⁻¹, 1 + (12N)⁻¹). The coefficient multiplying the exponent in $(\begin{array}{c}N\hfill \\ k\hfill \end{array})/{(\begin{array}{c}m\hfill \\ k\hfill \end{array})}^2$ is

$$\sqrt{2\pi k}{(1-k/N)}^{-1/2}(1-k/m)~\sqrt{\pi \beta m}(1-\beta /2)\to \infty$$

under our assumptions, and this yields (A.38).