Figure 5.
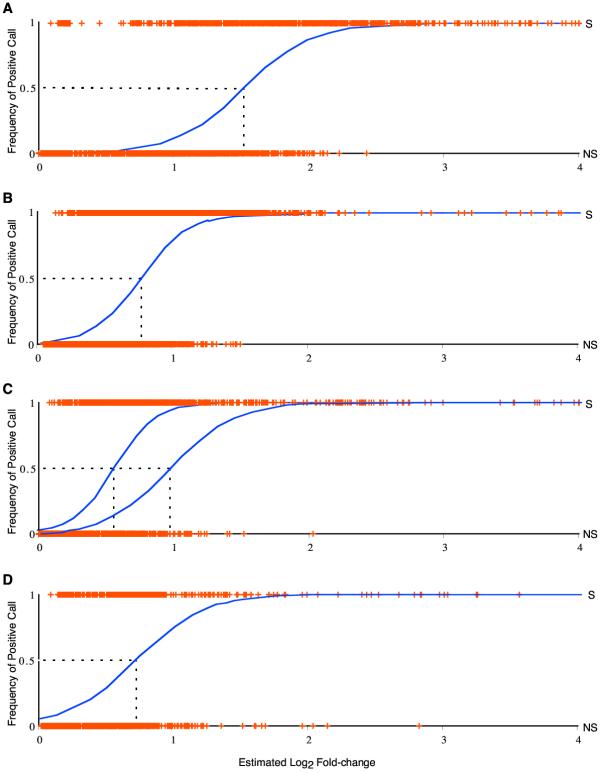
Logistic regressions of the probability of detection of gene expression differences from experimental data. Logistic regressions of the frequency of affirmative significance call on the estimated log2 factor of difference in gene expression for five datasets from four published studies that publicly reported replicated ratio results for each hybridization. The logistic model plotted is that loge(p/(1 - p)) = mx + b, where p is the probability of an affirmative significance call, and x is the log2 factor of difference in gene expression. Cross symbols (+) are plotted at the estimated expression level of each gene, either at the top of the plot when identified as significant (S), or at the bottom when identified as not significant (NS). See Townsend and Hartl [8] and Townsend et al. [10] for diagrams of the experimental designs for these studies. Logistic regressions of significance call on the factor of difference are computed from the data of A) Alexandre et al. [27], comparing yeast in log-phase growth with yeast in log-phase growth after 30 minutes of exposure to high ethanol. The model has a highly significant fit (χ2 = 2126.4, P < 0.00001). The estimated intercept for the log odds, b, of an affirmative significance call is -6.0 (significant, P < 0.0001), and the estimated slope with log2 factor of difference in gene expression, m, is 4.0 (significant, P < 0.0001). Three microarray comparisons were performed on two samples. The factor of gene expression at which 50% of estimated differences were identified as significant (GEL50) was 2.8-fold. B) Lyons et al. [28], comparing expression in yeast in wild type and zap1 strains at log-phase growth in low zinc media. The model has a highly significant fit (χ2 = 2844.0, P < 0.00001). The estimated intercept for the log odds, b, of a significant call is -4.2 (significant, P < 0.00001), and the estimated slope with log2 factor of difference in gene expression, m, is 5.8 (significant, P < 0.0001). Nine microarray comparisons were reported on six samples, and GEL50 = 1.65-fold. C) Sudarsanam et al. [26], comparing expression in yeast between wild type and snf2 strains at log-phase growth in rich and minimal media. Cross symbols representing the data are plotted only for the left-hand curve, which regresses data from the comparison in minimal media. The model has a highly significant fit (χ2 = 2429.3, P < 0.00001). The estimated intercept for the log odds, b, of a significant call is -3.9 (significant, P < 0.00001), and the estimated slope with log2 factor of difference in gene expression, m, is 6.7 (significant, P < 0.0001). Six microarray hybridizations were performed between three samples, and GEL50 = 1.49-fold. The right-hand curve is from an experiment on rich media. The model has a highly significant fit (χ2 = 1458.7, P < 0.0001). The estimated intercept for the log odds, b, of a affirmative significance call is -4.0 (significant, P < 0.00001), and the estimated slope with log2 factor of difference in gene expression, m, is 4.3 (significant, P < 0.0001). The data were restricted to five microarray hybridizations among three samples, and GEL50 = 1.91-fold. D) Townsend et al. [10], comparing expression in two natural isolates of yeast at log-phase growth. The model has a highly significant fit (χ2 = 925.5, P < 0.0001). The estimated intercept for the log odds, b, of an affirmative significance call is -2.9 (significant, P < 0.0001), and the estimated slope, m, is 4.5 (significant, P < 0.0001). Ten microarray comparisons were performed among four samples, and GEL50 = 1.56-fold.
