Estimation of Drug Effectiveness by Modeling Three Time-dependent Covariates: An Application to Data on Cardioprotective Medications in the Chronic Dialysis Population

Abstract

In a population of chronic dialysis patients with an extensive burden of cardiovascular disease, estimation of the effectiveness of cardioprotective medication in literature is based on calculation of a hazard ratio comparing hazard of mortality for two groups (with or without drug exposure) measured at a single point in time or through the cumulative metric of proportion of days covered (PDC) on medication. Though both approaches can be modeled in a time-dependent manner using a Cox regression model, we propose a more complete time-dependent metric for evaluating cardioprotective medication efficacy. We consider that drug effectiveness is potentially the result of interactions between three time-dependent covariate measures, current drug usage status (ON versus OFF), proportion of cumulative exposure to drug at a given point in time, and the patient’s switching behavior between taking and not taking the medication. We show that modeling of all three of these time-dependent measures illustrates more clearly how varying patterns of drug exposure affect drug effectiveness, which could remain obscured when modeled by the more standard single time-dependent covariate approaches. We propose that understanding the nature and directionality of these interactions will help the biopharmaceutical industry in better estimating drug efficacy.

1. Introduction

An important aim of time-to-event analyses (also known as survival analyses) in health outcomes research is to identify important risk factors associated with the outcome of interest. The risk associated with the presence or absence of these factors must be quantified to enable meaningful comparison between individuals who possess these risk factors and those who do not. A Cox proportional hazards (PH) model (Cox 1972) is a commonly used survival analysis method that enables such comparisons to be made by means of calculating a hazard ratio, which can be thought of as the ratio of instantaneous risk of experiencing the outcome of interest in the two groups of individuals. The assumption that underpins this approach is that the proportionality of hazard for the outcome of interest remains constant throughout the observation window, and standard diagnostic methods are readily available to test this assumption. When the risk associated with the outcome of interest changes across time, the assumption of proportionality of hazards is violated, suggesting the presence of non-proportional hazards.

It is not uncommon in health outcomes research to encounter covariates that change values across time. Such “time-dependent covariates” have different values at baseline relative to some distant point in follow-up during the observation window. However, time-dependent covariates can be incorporated into a Cox regression framework by making suitable changes to the partial likelihood equation thereby permitting the likelihood to be comprised of different components at the distinct times at which the events occur. Each component, therefore, incorporates the (changed) value of the covariate at the time of a particular event. For example, when treatment is a dichotomous covariate (with, say, 0 representing no treatment and 1 representing treatment), the time-dependent framework of the Cox regression model is often used where subjects receive treatment only after some passage of time (Klein and Moeschberger 2003; Chapter 9). This framework allows identification of the time spent on and off treatment for each individual subject to be incorporated accordingly into the statistical model. As such, at each event time, one can identify the number of subjects in the risk set at that event time and their corresponding treatment status. Likewise, in the case of a continuous covariate that changes values across the observation window, one can incorporate into the model the covariate value for subjects belonging to the risk set every time an event is experienced by any subject in the cohort.

Though both categorical and continuous covariates can be handled in the time-dependent framework of the Cox model, there are situations in which it is uncertain how a particular time-dependent covariate should best be modeled. For example, in the case of time-to-event analysis of chronic dialysis patients, our objective is to quantify risks or benefits associated with receiving cardioprotective medications, with patient morbidity and/or mortality being designated as the outcome of interest. In this case, information is available regarding the patients’ medication usage through an algorithm which quantifies medication exposure based on drug prescribing records. Thus it is possible to identify alternating periods of medication exposure (herein referred to as use and non-use).

In the literature on medication usage, traditional ways of quantifying the hazard ratio of death for treatment versus no treatment crudely considers treatment to be a dichotomous variable, assigned at a single point in time (typically at the beginning of the observation period), thereby allowing analysis by means of a standard Cox PH model. The disadvantage of this approach is that medication use at baseline may not accurately reflect use over the course of the survival period. It is also common to see medication usage modeled in terms of a continuous covariates various called “proportion of days covered” (PDC) or “medication possession ratio”, so as to quantify drug effectiveness by estimating a hazard ratio of mortality per unit increase in the exposure metric. As with the previous approach, this approach may also misclassify subjects’ exposure times. For example, someone with a PDC of 0.5 may not have been a user until halfway through their survival time; and so their contributions to the estimation equation at early time periods would not accurately reflect this non-use at that later time. An alternative approach could incorporate medication usage (ON versus OFF) modeled as a time-dependent covariate in a Cox regression model. While this accurately reflects the current state of the exposure measure, important factors such as cumulative exposure, which may relate to more long-term physiologic processes such as vascular remodeling, would not be quantified by this approach. An adjustment to this approach, therefore, is to treat cumulative drug exposure as a time-dependent covariate and estimate the relative risk of the event of interest as a function of increasing drug exposure. For example, Maitland-van der Zee et al. (2004) have reported more accurate estimates of statin effectiveness comparable to results from randomized control trials using a dichotomized definition of cumulative drug exposure. However, in the context of our data (as discussed later in this paper), we show that a single time-dependent covariate may, in certain situations, fail to fully capture the nuances that lead to estimation of drug effectiveness.

In the present analysis, we develop a more comprehensive metric for modeling the time-dependent effect of medication that addresses these limitations. We suggest that, because drug efficacy is a complicated phenomenon in real world clinical scenarios, the “true” effects of medications on outcomes can be captured more accurately by considering three time-dependent metrics both individually and, as in a statistical interaction, in combination with each other. As drug efficacy can be affected by patients’ adherence (self or physician-directed), a more encompassing time-dependent metric may be needed to better explain medication effectiveness.

2. Motivating Example

Hypertension (HTN) and cardiovascular disease (CVD) are frequent in end stage renal disease (ESRD) patients on dialysis, with prevalence rates of 78% for HTN, 46% for coronary artery disease, 29% for congestive heart failure (CHF), and 17% for cerebrovascular disease (cerebrovascular accident, CVA, and/or transient ischemic attack, TIA) with adverse impacts on patient mortality and morbidity (Lopes et al. 2009). The 3-year event rates after chronic dialysis initiation are 21% for acute myocardial infarction (AMI), 41% for CVA/TIA, and 72% for CHF. Fully 85% of these patients die in the first three years on dialysis as per the United States Renal Data System Annual Report (2006), the majority from manifestations of cardiovascular disease. Currently, antihypertensive agents with the most well established cardio-protective properties are renin-angiotensin-aldosterone system inhibitors (angiotensin converting enzyme inhibitors, ACEIs, and angiotensin receptor blockers, ARBs), beta-adrenergic blockers (β-blockers), and calcium channel blockers (CCBs). Most of the published literature aimed at studying the effectiveness of these cardio-protective medications excludes persons on chronic dialysis. (Yusuf et al. 2000). Despite the fact that two meta-analyses studies derived from patients with ESRD (Heerspink et al. 2009 and Agarwal and Sinha 2009) reported evidence of efficacy in reducing all-cause and cardiovascular mortality and cardiovascular events, issues of publication bias dampened these conclusions with the authors calling for adequately powered trials to confirm their results. Several observational studies have examined the effectiveness of these medications in chronic dialysis cohorts but have faced a number of shortcomings (Wetmore and Shireman 2009).

To bridge the gaps in knowledge, we conducted an observational study to assess the effectiveness of cardio-protective antihypertensive medications in reducing mortality and morbidity in a dialysis population. In this study, Medicaid prescription claims were linked with the United States Renal Data System (USRDS) registry data and Medicare claims for 52,922 hypertensive chronic dialysis patients. Details of data linkage algorithms with clinical justifications can be found elsewhere (Shireman et al., submitted). We present results of our approach for each class of drug, that is, ACEI-ARBs, β-blockers, CCBs considered individually as well as for combined classes (any out of ACEI-ARBs, β-blockers, or CCBs). In each case, the most parsimonious model is presented. In order to validate our model, we also discuss results from modeling an “inert” drug (Levothyroxine) the intake of which is not expected to benefit patient mortality or morbidity, as it is indicated only for the treatment of hyperthyroidism.

3. Estimation of Treatment Effectiveness including Three Time-dependent Covariates

3.1 Time-dependent Covariates

Covariates that do not change values across time are considered to be time-independent covariates (e.g., gender, race, baseline age, blood pressure and weight at dialysis initiation). Treatment membership in a randomized clinical trial where patients are randomized in two groups to receive either placebo or treatment is also an example of a time-independent covariate since treatment membership remains constant across time. Conversely, covariates that can assume different values over time are considered to be time-dependent covariates.

Kalbfleisch and Prentice (1980; Chapter 6) distinguish between two types of time-dependent covariates: external covariates and ancillary covariates. External time-dependent covariates are those whose values at any time do not depend on the survival process such as in the case of planned schedule of treatments under the control of the investigator. On the other hand, internal time-dependent covariates are those which involve time measurements taken on an individual with the covariates being measures only as long as the individual is part of the risk set, thereby carrying information about the survival process. For example, in the Stanford Heart Transplantation Program (see Elandt-Johnson and Johnson 1980), aimed at assessing the effect of a heart transplant in a cohort of patients, transplant status may be considered to be an internal time-dependent covariate. In this case, some patients never receive a heart transplant and so their transplant status (denoted by 0) remains unchanged, while some other patients receive a transplant at some point of time in the observation window causing a change in their transplant status (from 0 to 1). Likewise, in a retrospective study for assessing risk of stroke in patients with atrial fibrillation (AF) in a dialysis population, AF may be considered to be a time-dependent covariate with many patients starting the study in an AF-free state but developing AF at some point in the time window (Wetmore at al. 2012). Allison (2012; Chapter 5) has discussed how more complicated scenarios in the time-dependent covariate framework can be envisioned in the sense that such time-dependent covariates can:

1. change values at regular intervals that agree with the time units in which events are observed;

2. change values at regular intervals that do not agree with the time units in which events are observed;

3. change values at irregular intervals.

Literature on time-dependent covariates suggests many different functional forms of time for handling the different scenarios listed above. For example, in the simulated data on patients suffering from alcoholic cirrhosis that aimed to study the effect of blood coagulation time (time-dependent covariate) on patient survival, Allison (2012; Chapter 5) has considered ‘closest preceding measurement’ as the appropriate functional form for this time-dependent covariate. Using an appropriate functional form of time, time-dependent covariate information can be incorporated in the regression framework of a Cox model such that the likelihood at each event time contains the information about the values assumed by the covariate at that particular event time for all patients who are alive at that time point. Key issues related to the selection of the functional form of a time-dependent covariate in a clinical context have been discussed in Fisher and Lin (1999).

3.2 Incorporating Time-dependent Covariates in a Cox Regression Model

A Cox PH model for comparing hazards associated with receiving treatment as opposed to not receiving treatment is given by:

$$h(t\mid z)=h_0(t)exp(\beta Z)$$ (1)

where Z = 1 if patient receives the treatment and 0 otherwise, h₀(t) is some baseline hazard associated with the cohort, and β is the regression coefficient associated with the dichotomous treatment variable (Allison 2002). Thus for patients who do not receive treatment, h(t|Z = 0) = h₀(t) and for patients who receive treatment h(t|Z = 1) = h₀(t)exp(β). This facilitates calculation of a hazard ratio (HR) for the outcome of interest (say death) given by HR = exp(β) which has the interpretation that hazard of death for those receiving treatment is exp(β) times the hazard of death who do not receive the treatment. Clearly, β > 0 implies harmful effect of treatment and β < 0 implies protective effect of treatment. Estimation of β is based on maximizing the partial likelihood given by:

$$PL={\prod }_{i=1}^D{L}_i={\prod }_{i=1}^D\frac{exp(\beta Z_i)}{{\sum }_{j\in R(t_i)}exp(\beta Z_j)}$$ (2)

where D = total number of distinct event times, R(t_i)is the number of subjects in the risk set at a given event time t_i, and z_i is the covariate value for the person experiencing the event at t_i.

Equation 1 mentioned above assumes that the HR of death is constant across the observation window. In other words, the hazard of death for those receiving treatment is proportional to the hazard of death for those not receiving treatment, with exp(β) being a measure of this proportionality. Whether or not this proportionality of hazards assumption is true, can be assessed by means of diagnostic checking procedures found in standard statistics texts. One such diagnostic checking procedure involves assessing the statistical significance of the interaction effect between the covariate of interest and time. Thus, in this case, equation (1) is modified to:

$$h(t\mid z)=h_0(t)exp\{{\beta }_{1}Z+{\beta }_{2}Z(t)\}$$ (3)

Here β₁ is the regression coefficient associated with the covariate alone while β₂ is the regression coefficient associated with the interaction effect of the covariate with time. If β₂ is statistically significant, then the HR of death for treatment versus no treatment is given by exp{β₁ + β₂t}. Clearly, this is a function of time implying that the HR is not constant over time. It should be noted that in the case of the model represented by equation (3), estimates of β₁ and β₂ are obtained by maximizing the partial likelihood given by:

$$PL={\prod }_{i=1}^D{L}_i={\prod }_{i=1}^D\frac{exp\{{\beta }_1{Z}_i+{\beta }_2{Z}_i(t)\}}{{\sum }_{j\in R(t_i)}exp\{{\beta }_1{Z}_j+{\beta }_2{Z}_j(t)\}}$$ (4)

Equation (3) can easily be expanded to accommodate other risk factors that may or may not satisfy the proportionality assumption for the hazard of death associated with these risk factors. The basic form of equation (3) can be used to account for time-dependent covariates; however, the computations required for the resulting partial likelihood (such as the one in equation (4)) are more involved. Specifically, a separate partial likelihood is computed at each unique event time for all individuals who are part of the risk set with each individual contributing his time-specific covariate value to the likelihood. The overall partial likelihood is formed by multiplying these separate partial likelihoods over all unique event times, and is then maximized to obtain the estimates of the regression coefficients.

3.3 Modeling Drug Effectiveness using Three Time-Dependent Covariates

In this section, we will demonstrate how three time-dependent covariates along with their interaction effects can be used to estimate the effectiveness of various cardio-protective antihypertensive medications on mortality in a dialysis population in our retrospective study. We begin by noting that algorithms on the patients’ prescription records developed by this team of researchers have enabled the tracking of weekly medication usage for patients belonging to this cohort. Thus, it is possible to identify whether or not a patient had the medication at any given week during the study period. Thus medication status (DRUG = ON versus DRUG = OFF) can be recorded dichotomously (1 or 0) for every week the patient is part of the cohort. In a single covariate (time-independent) model, if the medication possesses a cardio-protective effect, HR of death for being ON drug versus being OFF drug is expected to be less than unity. Likewise, in a single covariate (time-independent) model with a continuous proportion of days covered (proportion of days with medication based on prescriptions, or PDC) variable replacing the dichotomous DRUG variable, a HR less than unity would imply an increase in PDC confers a protective benefit on mortality.

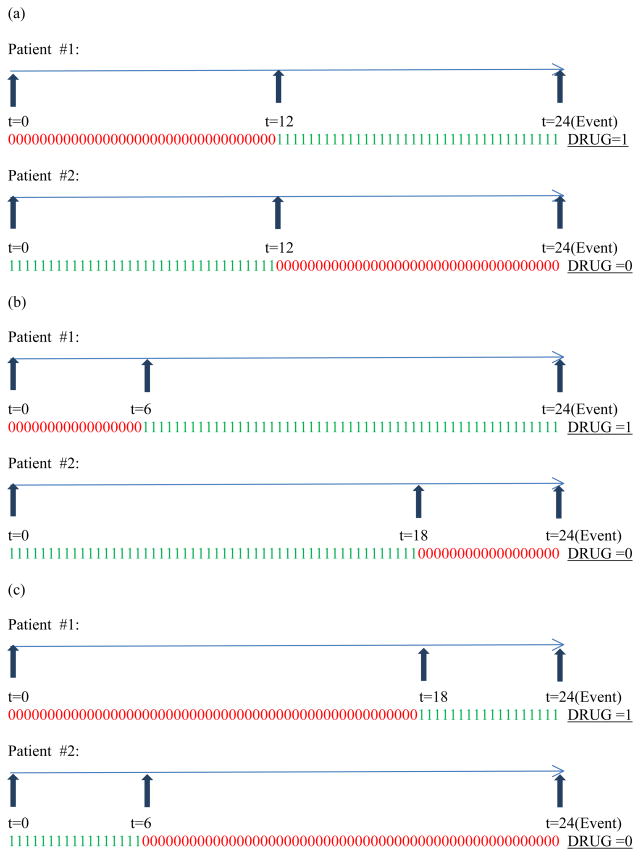
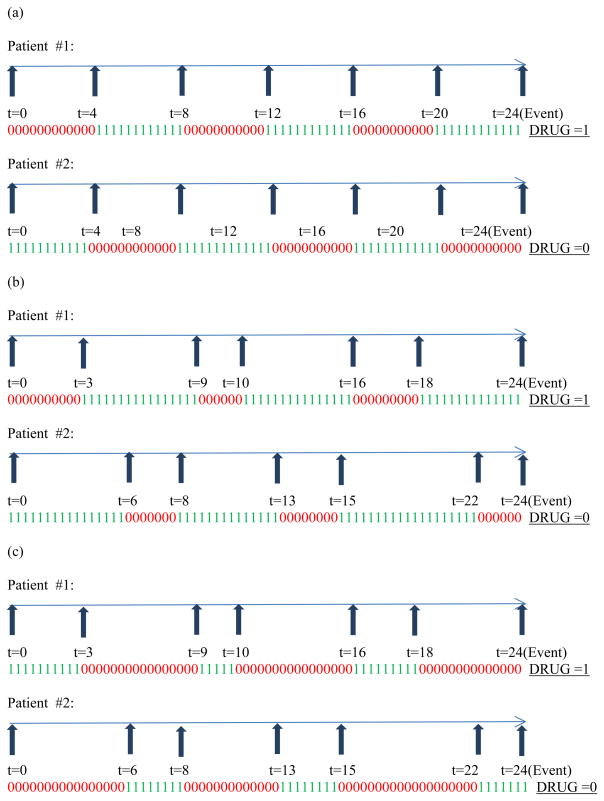
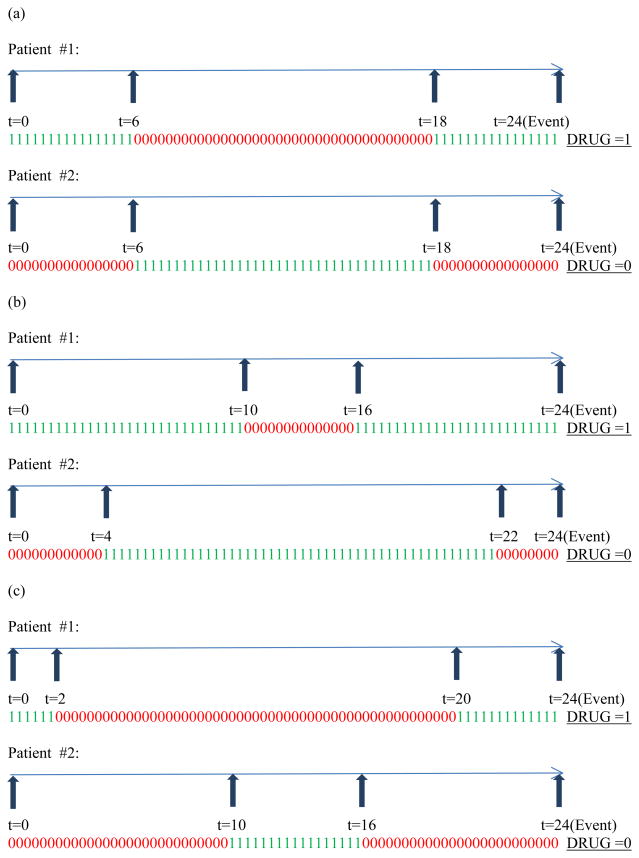
To show that such univariate modeling using either DRUG or PDC is inadequate, we consider a gamut of medication usage patterns relevant to patients belonging to this cohort. Figure 1 through Figure 3 display the various weekly medication usage patterns with a horizontal arrow representing the time axis with each 1 or 0 indicating the ON or OFF status (respectively) of medication during that week. Vertical arrows indicate the week at which change of covariate status for DRUG takes place. In our discussion related to these figures, we assume that the effect of all other risk factors such as age, gender, race, and other comorbidities has been adjusted with the assumption of proportional hazards holding true for these risk factors. As complete information about the weekly DRUG status of patients is available, we intend to incorporate DRUG as a time-dependent covariate so that the contribution to the likelihood computed at each event time reflects the current DRUG status.

Figure 1.

Varying patterns of medication usage for only one switch in DRUG status

Figure 3.

Varying patterns of medication usage for five switches in DRUG status

Figure 1 (a) through (c) represent situations for two patients who differ in their medication usage patterns with the variable DRUG changing status only once. Likewise Figure 2 (a) through (c) and Figure 3 (a) through (c) represent situations for two patients who differ in their medication usage patterns with the variable DRUG changing status exactly two times and exactly five times, respectively. Detailed explanation of how these patterns influence the creation of three time-dependent covariates has been explained in Appendix A. Briefly, studying the patterns in parts (a) through (c) of each figure (Figure 1 or 2 or 3) in isolation leads us to the creation of a second time-dependent covariate CUMPWC (cumulative proportion weeks covered), representing the PDC up to the current point in time. CUMPWC can be considered both as a main effect as well as in interaction with current DRUG status. Also, when these figures are compared to each other, we find that only modeling DRUG, CUMPWC and the DRUG*CUMPWC interaction is inadequate in terms of distinguishing distinct medication patterns. To this end, we introduce a third time-dependent covariate SWITCHNUM (number of alterations in DRUG status) and also consider its interaction with DRUG and CUMPWC. Finally, a three-way interaction term strengthens the model leading to a full starting model with the following terms:

Figure 2.

Varying patterns of medication usage for two switches in DRUG status

DRUG, CUMPWC, SWITCHNUM, DRUG*CUMPWC, DRUG*SWITCHNUM, CUMPWC*SWITCHNUM, and DRUG*CUMPC*SWITCHNUM

We envision this model to explain important aspects of medication effectiveness hitherto unexplained by simple single covariate models. Various scenarios related to different values of DRUG, CUMPWC and SWITCHNUM have been discussed in greater detail in Appendix B. Although, a model with a three-way interaction seems complex, it could prove vital to understanding cardio-protective medication efficacy. It is quite conceivable that medication effectiveness in the patients’ blood stream at any given point in time depends on their current ON/OFF medication status, their overall cumulative exposure to the medication, and their consistent (or compliant) use of their medication. For example, abrupt cessation of treatment with beta-blockers has been reported to increase the risk of myocardial infarction in patients with hypertension as discussed in Teichert et al. (2007). Likewise, Vacek (1997) discusses how ignoring the complex time-varying nature of drug exposure or restricting its modeling to a subset of its components, such as only current dose or only duration of exposure, may miss more complex forms of association between exposure and outcome or lead to etiologically incorrect conclusions. Sylvestre and Abrahamowicz (2009) show how in the framework of Cox PH models, cumulative effects of time-varying exposures can be weighted by their recency, the weights being estimated by cubic regression splines.

3.4 Relating the Three Time-dependent Covariate Model to a State Transition Model

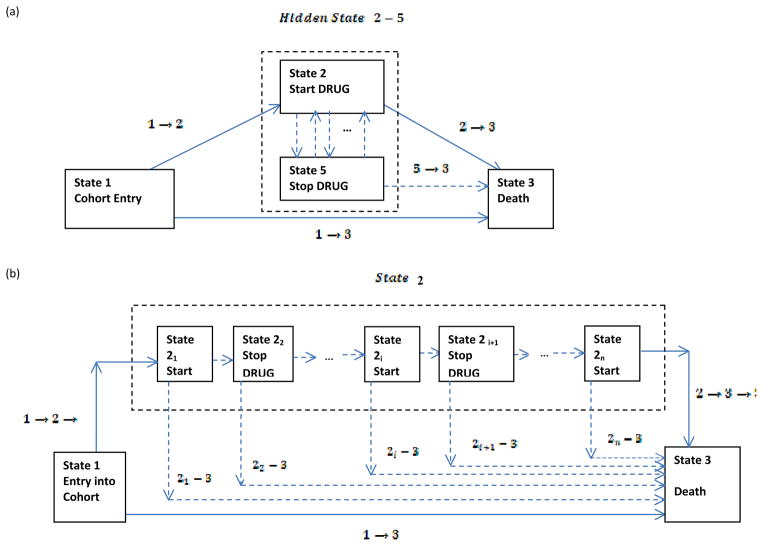
The three time-dependent covariate model mentioned in the earlier section can also be arrived at using the modeling approach of state transition models. Putter, Fiocco and Geskus (2007) show the equivalence between a single time-dependent covariate model and a single state transition model under the Markov proportional hazards assumption. Figure 4 shows such a single state transition model which considers three possible states of existence. State 1 is the initial state called the ‘Drug-free’ state. State 2 is the single intermediate state in which a patient starts taking the drug. State 3 is the third terminal and absorbing state representing death (or censored for those who alive). Thus it is possible to transition from State 1 to State 3 directly or through State 2. By the Markov assumption it is meant that what happens to a patient in a particular state depends only the fact that he or she is in that state and not on the history preceding it.

Figure 4.

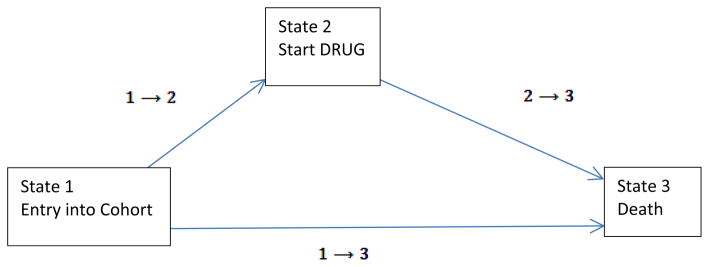
Single-state transition model as an alternative to single time-dependent covariate model

Denoting h_ij as the transition hazard for moving from state i to state j their model is:

$$h_{i3}(t)=h_{3_0}(t)exp\{{{\mathit{\beta }}_{\mathbf{13}}}^{\prime }\mathbf{Z}+(i-1){\mathrm{\Delta }}^{\prime }\mathbf{Z}+(i-1)\delta \},i=1,2$$ (5)

Here h₃₀(t) represents some baseline hazard attributable to state 3, β₁₃ represents the vector of regression coefficients for the other risk factors, Z is the vector of risk factors, Δ represents the difference in covariate effects of these other risk factors for death after taking drug, compared to before taking drug, and δ represents the estimate of the drug effect. Using equation (5), we can obtain h₁₃ and h₂₃ as:

$$h_{13}(t)=h_{3_0}(t)exp\{{{\mathit{\beta }}_{\mathbf{13}}}^{\prime }\mathbf{Z}\}$$ (6)

$$h_{23}(t)=h_{3_0}(t)exp\{({{\mathit{\beta }}_{\mathbf{13}}}^{\prime }+{\mathrm{\Delta }}^{\prime })\mathbf{Z}+\delta \}$$ (7)

As the proportionality of hazards assumption is true for the other risk factors, we can write β₁₃′ + Δ′ = β₂₃′ and simply equation (7) further. Equation (7) can be rewritten in the time-dependent framework of a Cox regression model as:

$$h_3(t)=h_{3_0}(t)exp\{({{\mathit{\beta }}_{\mathbf{23}}}^{\prime })\mathbf{Z}+\delta .\text{DRUG}(t)\}$$ (8)

where DRUG(t) equals 0 for all t before patients start taking medication and 1 for after they start taking medication. Thus a single state-transition model can be expressed as a single time-dependent covariate model. More detailed examples which analyze multi-state models with more than one intermediate states and end points can be found in the breast cancer study analysis by Putter et al. (2006) and in the bone-marrow transplantation study analysis by Klein, Keiding and Copelan (1994).

As explained in Section 3.3, a single time-dependent covariate model using DRUG alone appears inadequate for the data under concern. In other words, Figure 4 is not an adequate representation of our intended model and can be manipulated to obtain a single state transition model with hidden states as shown in Figure 5. Motivated by the discussion on hidden state models by Hougaard (2001; Chapter 5), in Figure 5 we consider state 5 as a hidden state in which a patient stops taking medication. Thus it is possible to transition from state 2 to state 5 and from state 5 back to state 2 in addition to transitioning from state 2 to state 3 and from state 5 to state 3. Multiple transitions are possible between state 2 and state 5 with each transition representing a switch between being ON drug and OFF drug. In fact, state 2 and state 5 combined can be thought of as a single state named ‘Ever Drug?’ (state 2-5). In that case, the single state transition model of equation (7) and equation (8) is still valid with state 2-5 (Ever Drug?) replacing state 2. In terms of the time-dependent covariate framework of the Cox regression model, equation (8) will have to be modified to:

$$h_3(t)=h_{3_0}(t)exp\{({{\mathit{\beta }}_{\mathbf{2}-\mathbf{5},\mathbf{3}}}^{\prime })\mathbf{Z}+\delta .{\text{DRUG}}_{2-5}(t)\}$$ (9)

with β_2–5.3 representing the vector of coefficients for other risk factors that are affected through the state 2-5 (Ever Drug?) transition, and DRUG_2–5(t) equals 0 for all t before patients start taking medication and 1 for after they start taking medication. In this case, the effect of switching (represented by SWITCHNUM from Section 3.3) and cumulative drug exposure (represented by CUMPWC in Section 3.3) will be masked by a single DRUG_2–5(t) covariate term. To isolate these effects from DRUG_2–5(t) we will have to consider the two possible hidden state representations shown in Figure 5(a) and (b). It can be seen through Figure 5(b) that there can be many sub-transitions from state 2 to state 3 represented by 2_i, 3 with i equaling the number of switches between state 2 and state 5. Each transition would then have its own sub-transition hazard and in the context of the Markov proportional hazards model, we would require a separate model for each sub-transition. Additional parameters would need to be added in the model for each sub-transition hazard to account for incremental hazard effects specific to that particular sub-transition. Instead we prefer the diagrammatic representation of Figure 5(a) as it allows us to simultaneously look at our model as a single state (state 2-5) transition model with a hidden state (state 5). This allows us to break the single DRUG_2–5(t) covariate term into various components as shown below:

$$\begin{array}{l}{h}_3(t)=h_{3_0}(t)exp\{({{\mathit{\beta }}_{\mathbf{2}-\mathbf{5},\mathbf{3}}}^{\prime })\mathbf{Z}+{\delta }_1.\text{DRUG}(t)+{\delta }_2.\text{CUMPWC}(t)+{\delta }_3.\text{SWITCHNUM}(t)\}+\\ {\delta }_4.\text{DRUG}(t).\text{CUMPWC}(t)+{\delta }_5.\text{DRUG}(t).\text{SWITCHNUM}(t)+\\ {\delta }_6.\text{CUMPWC}(t).\text{SWITCHNUM}(t)+{\delta }_7.\text{DRUG}(t).\text{CUMPWC}(t).\text{SWITCHNUM}(t)\}\end{array}$$ (10)

Figure 5.

Two representations of a hidden state model for the single state transition model of Figure 4

Here DRUG(t) equals 0 if patient is in state 5 (OFF drug) at time t and 1 if patient is in state 2 (ON drug) time t, CUMPWC(t) equals the cumulative drug exposure at time t, SWITCHNUM(t) equals the number of transitions from state 2 to state 5, and the higher order terms represent corresponding two-way and three-way interactions. The regression coefficients for each of these terms are represented by δ_i (i = 1 to 7). Without loss of generality, the vector of regression coefficients β_2–5,3 for the vector other risk factors Z can be replaced by β. This effectively is the model we have discussed in Section 3.3. By modeling three time-dependent covariates and their interaction terms in a Cox regression framework, we can assess different aspects of the medication effectiveness.

4. Results

Descriptive statistics for risk factors other than medication effectiveness and their corresponding adjusted hazard ratios (AHRs) can be found in the upcoming paper by Shireman et al. Tables 1–4 display the AHRs for mortality for various cardio-protective medications. These were obtained using equation (9) with the AHRs for only the most parsimonious models computed.

Table 1.

Adjusted hazard ratios (AHR)* for mortality using time-dependent drug exposure measures comparing active use of selected antihypertensive agents to non-use accounting for number of switches and percentage of prior weeks with medication

% preceeding weeks with drug	Any Drug (ACEARBS or BetaBlockers or CCBs)				BetaBlockers
	# switches				# switches
	1	2	5	10	Any
10	0.673 [0.592–0.765]	0.695 [0.616–0.784]	0.766 [0.675–0.869]	0.901 [0.730–1.113]	0.754 [0.682–0.834]
25	0.650 [0.584–0.723]	0.664 [0.603–0.736]	0.718 [0.650–0.794]	0.813 [0.692–0.956]	0.723 [0.667–0.784]
40	0.628 [0.575–0.686]	0.639 [0.589–0.694]	0.673 [0.623–0.727]	0.734 [0.654–0.825]	0.693 [0.649–0.741]
50	0.614 [0.567–0.664]	0.621 [0.577–0.669]	0.645 [0.604–0.688]	0.686 [0.627–0.750]	0.674 [0.634–0.717]
60	0.600 [0.557–0.646]	0.604 [0.564–0.647]	0.618 [0.583–0.654]	0.641 [0.597–0.688]	0.655 [0.616–0.697]
75	0.579 [0.538–0.624]	0579 [0.541–0.620]	0.579 [0.546–0.614]	0.578 [0.539–0.621]	0.628 [0.586–0.676]
90	0.560 [0.515–0.608]	0.555 [0.514–0.600]	0.543 [0.504–0.584]	-	0.603 [0.552–0.657]

Table 1 (left panel) displays the AHR of mortality for DRUG (ON versus OFF) for the combined medication (any of ACEIs, ARBs, β-blockers, CCBs) using the full model with the three-way interaction term represented in equation (9). As δ̂₇ was statistically significant at the 0.01 level of significance, all other δ_i were retained in the model using the principle of model hierarchy. With reference to equation (9), the AHR of death for DRUG (ON versus OFF) was calculated for different levels of CUMPWC (first column of Table 1) and SWITCHNUM (second through fifth column of left panel of Table 1). Thus, for SWITCHNUM = 1, AHR of death for DRUG (ON versus OFF) when CUMPWC = 10% is 0.673 (99% CI: 0.592–0.765) and decreases to 0.560 (99% CI: 0.515–0.608) when CUMPWC = 90% indicating a significant protective effect of being on medication. The value of SWITCHNUM = 1 (second column in Table 1) represents the medication usage pattern discussed in Figure 1. Thus at the time of an event, the hazard of patient #1 who has been taking medication for 10% of the time immediately preceding the event is compared to the hazard of patient #2 who has not been taking medication 90% of the time immediately preceding the event. The AHR is a ratio of these two hazards and represents the relative protective effect of being on medication given a solitary change in DRUG status and cumulative weekly drug exposure of 10%. Similarly, for SWITCHNUM = 10 (fifth column in Table 1), AHR of death for DRUG (ON versus OFF) when CUMPWC = 10% is 0.901 (99% CI: 0.730–1.113) and decreases to 0.578 (99% CI: 0.539–0.621) when CUMPWC = 75%. This suggests that when patients frequently change their medication status resulting in lesser medication exposure over successive weeks, the protective effect of medication is waned off at low levels of cumulative exposure though a significant protective benefit is still maintained at high levels of cumulative exposure. This differential change in AHRs of death for DRUG across the varying levels of CUMPWC and SWITCHNUM is indicative of the statistically significant three-way interaction term from equation (9).

We can also try to understand the more comprehensive nature of this interaction by fixing CUMPWC at a fixed value and then moving across the columns of SWITCHNUM values. Thus, for low values of cumulative exposure, AHR of death for DRUG (ON versus OFF) increases as SWITCHNUM increases (patients shuffle frequently between taking and not taking medication). For higher values of cumulative exposure such as 75%, AHR of death for DRUG (ON versus OFF) is fairly stable at a point estimate of 0.579 irrespective of the patients’ switching patterns.

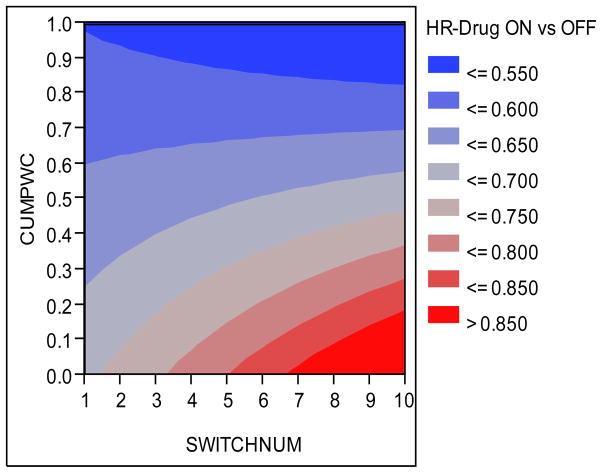
The heat map of Figure 6 can be particularly helpful and visually appealing in understanding this phenomenon. It plots the point estimate AHR of (any) DRUG (ON versus OFF) as a function of CUMPWC and SWITCHNUM on the y and x axes respectively. Protective effect of medication is represented by various shades of blue (darker is more protective) with shades of red representing the waning of the protective effect of medication (darker is less protective). From this heat map it can be seen that the beneficial effect of cardio-protective medications is highest and stable when cumulative drug exposure is higher than 75% irrespective of the switching pattern. The beneficial effect of medication is also appreciable if cumulative drug exposure is less (say < 50%) but patients have switched less frequently, perhaps, indicating that the medication works provided patients adhere to it continually for successive weeks. The protective effect of medication seems to wane off when patients frequently switch ON and OFF drug resulting in less cumulative exposure.

Figure 6.

AHR of (any) DRUG (ON vs OFF) as a function of CUMPWC and SWITCHNUM

For ACE/ARBs, the most parsimonious model was the model with the main effect of DRUG only. In this case, neither the main effect of CUMPWC, nor the main effect of SWITCHNUM, nor any of the two-way or three-way interactions was significant. The AHR of death for DRUG (ON versus OFF) was 0.607 (99% CI: 0.581–0.634) suggesting a protective effect of taking ACE/ARBs as opposed to not taking it.

For β-blockers (right panel of Table 1), the most parsimonious model was the model with all three main effects and two two-way interaction: DRUG* CUMPWC and CUMPWC*SWITCHNUM. Thus, the AHRs for DRUG (ON vs OFF) shown in the table are independent of the number of switches. The overall conclusions are similar to those from the any-medication model in that for fixed number of switches, the most beneficial effect of BBs is found for higher levels of CUMPWC and vice versa.

For CCBs (see second column of Table 2), the most parsimonious model consisted of only the DRUG, CUMPWC and DRUG*CUMPWC interaction with all other two-way and three-way interaction terms involving SWITCHNUM turning out to be not statistically significant at the 0.01 level of significance. Thus the results for CCBs (second column of Table 2) are easier to interpret. It can be seen that the AHR of death for DRUG (ON versus OFF) went from 0.634 (99% CI: 0.565–0.713) at CUMPWC = 10% to 0.529 (99%CI: 0.488–0.573) at CUMPWC = 90%. This implies that the protective benefit of CCBs increases slightly as medication exposure increases.

Table 2.

Adjusted hazard ratios (AHR)* using time- dependent drug exposure measures comparing active CCB use to non-use accounting for percentage of prior weeks with medication

% preceding weeks with drug	AHRs [99% CI] Mortality model	AHRs [99% CI] Morbidity model
10	0.634 [0.565–0.713]	1.107 [1.009–1.215]
25	0.613 [0.558–0.673]	1.035 [0.960–1.116]
40	0.592 [0.550–0.639]	0.968 [0.910–1.030]
50	0.579 [0.542–0.619]	0.926 [0.875–0.980]
60	0.566 [0.532–0.603]	0.886 [0.838–0.936]
75	0.547 [0.512–0.585]	0.828 [0.779–0.880]
90	0.529 [0.488–0.573]	0.775 [0.719–0.834]

In the third column of Table 2, we have shown the results of modeling cardio-vascular morbidity as the outcome of interest in place of mortality for investigating the cardio-protective effect of CCBs in order to discuss some interesting results regarding the interpretation of the AHR of death for DRUG (ON versus OFF) for fixed values of CUMPWC. In this model also, only DRUG, CUMPWC and the DRUG*CUMPWC interaction term was statistically significant. From the third column of Table 2 it can be seen that CCBs confer a protective benefit only when the cumulative exposure to them is greater than 50%. Thus for CUMPWC = 50%, AHR of cardio-vascular event for DRUG (ON versus OFF) is 0.926 (99% CI: 0.878–0.980) whereas for CUMPWC = 90%, the AHR goes down appreciably to 0.775 (99% CI: 0.719–0.834). When the cumulative exposure is between 25% and 50%, CCBs appear to be neither protective nor harmful as the 99% confidence intervals around the point estimates of AHR include the value of 1. Interestingly, when cumulative exposure is as less as 10%, being ON medication seems to render a harmful effect as compared to being OFF medication (AHR = 1.107; 995CI: 1.009–1.215). One possible explanation for this reversal of AHR value is that patients with low cumulative exposure to medication have spent too many successive weeks without medication making them more susceptible to experiencing a cardio-vascular event even when they are currently on medication.

We also validated the results of our three-way time-dependent covariate model using an inert medication (Levothyroxine), which is intended to treat hyperthyroidism and would not be expected to offer any clinically meaningful mortality or morbidity (cardio-vascular event) benefits to its users. On doing so, we found that none of the regression coefficients related to the main effect, two-way interaction effect, or three-way interaction effect were statistically significant at the 0.01 level of significance. Using the appropriate contrast statement using PROC PHREG in SAS, we estimated the AHR of cardio-vascular event for DRUG_{Levothyroxine} (ON versus OFF) to be 0.919 (99% CI: 0.798–1.057) suggesting that Levothyroxine is indeed an inert medication not affecting patient mortality. Similarly, the AHR of death for DRUG_{Levothyroxine} (ON versus OFF) after adjusting for other medications was estimated to be 0.952 (99% CI: 0.762–1.189) indicating no significant benefit or harm. These results suggest that the type I error rate for our models was not inflated.

5. Discussion

Estimation of effectiveness of medications can be quite challenging when medication usage patterns vary across patients. This is particularly true when patients have multiple periods of successively taking and not taking their medication. In such situations, it is difficult to estimate medication efficacy by means of a single covariate approach using a dichotomous ‘Ever versus Never’ categorization of medication or by using PDC. The time-dependency of medication usage resulting from myriad medication usage patterns plays a key role in determining how these medications can potentially benefit or not benefit patients. By incorporating in the Cox regression framework, a more comprehensive metric involving three main time-dependent factors (and all related interaction terms), one can capture the role that medication usage patterns play in determining their effectiveness. By allowing the risk of taking (versus not taking) medication to vary differentially across cumulative drug exposure and patient’s switching patterns, important aspects of medication efficacy can be studied. We can, therefore, better isolate medication patterns that result in protective, ineffective, or even harmful effects. When higher order interactions are not significant, the most parsimonious models resulting from this approach can accord simplistic interpretations of hazard ratios that are consistent with single covariate approaches.

5.1 Limitations

Some limitations to our approach are inevitable. One limitation is that the medication usage patterns are assumed to match the patients’ prescription records available to us. Though this may not always be true, in the absence of accurate information about patient’s actual medication intake, prescription records provide a reasonable working solution. Another limitation is the metric of CUMPWC which models cumulative exposure in weeks. Thus, a patient who took the medication for only a day of the week is treated the same as another patient who diligently took the medication all seven days of the week. The SWITCHNUM variable, thus, reflects the switching behavior of patients on a weekly metric of time. Our justification of using weeks as the unit of time is based on practical considerations emerging from our discussion with clinicians working with cardio-protective medications. As our data is from the six year period of 2000–2005, we need to track ON/OFF medication status of patients for a maximum of 313 weeks. Using days instead of weeks would induce significant additional computational burden on the estimation of the regression coefficients using the partial maximum likelihood equation. On the other hand, using months instead of weeks would not appropriately capture medication effectiveness especially with reference to the role played by the SWITCHNUM variable.

Another limitation is that the three-way interaction captured in our model is with reference to either the individual classes of drugs or for the combined usage of ‘any’ drug. It does not capture the complexity at the level of inter-drug interactions (interaction effects across usage patterns of different drugs). However, our main intent in this paper is to show the role that medication usage patterns play toward estimating drug effectiveness and to that end our model has recognizable real life interpretation.

5.2 Conclusions

In our application to the data on cardio-protective medications in chronic dialysis population, we found that mortality benefits were conferred by ACE/ARBs, β-blockers, CCBs. For use of any type and for individual use of β-blockers, the three-way interaction was statistically significant whereas for ACE/ARBs only the main effect of taking medication was statistically significant. In the case of the mortality model and the cardio-vascular morbidity for CCBs, only one two-way interaction term involving medication usage and cumulative drug exposure was statistically significant. For the mortality model, protective benefit of CCBs improved with increased drug exposure whereas for the cardio-vascular morbidity model, CCBs were effective only for higher levels of drug exposure with very low levels of drug exposure proving slightly harmful.