Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Oct 21;4:6691. doi: 10.1038/srep06691

Order-disorder phase transitions in the two-dimensional semiconducting transition metal dichalcogenide alloys Mo1−xWxX2 (X = S, Se, and Te)

Li-Yong Gan 1,*, Qingyun Zhang 1, Yu-Jun Zhao 2, Yingchun Cheng 1, Udo Schwingenschlögl 1,a
PMCID: PMC4204064  PMID: 25331363

Abstract

A combination of density functional theory, an empirical model, and Monte Carlo simulations is used to shed light on the evolution of the atomic distribution in the two-dimensional semiconducting transition metal dichalcogenide alloys Mo1−xWxX2 (X = S, Se, and Te) as a function of the W concentration and temperature. Both random and ordered phases are discovered and the origin of the phase transitions is clarified. While the empirical model predicts at x = 1/3 and 2/3 ordered alloys, Monte Carlo simulations suggest that they only exist at low temperature due to a small energetic preference of Mo-X-W over Mo-X-Mo and W-X-W interactions, explaining the experimental observation of random alloy Mo1−xWxS2. Negative formation energies point to a high miscibility. Tunability of the band edges and band gaps by alteration of the W concentration gives rise to a broad range of applications.

Two-dimensional materials often exhibit unique features, distinctly different from those of their bulk counterparts, and thus are receiving tremendous attention1,2,3. In particular, monolayers of semiconducting transition metal dichalcogenides, such as MoS2 and WS2, have versatile electronic4,5,6,7,8, optical9,10,11, mechanical12,13,14, and chemical15,16,17 properties, opening up new fundamental as well as technological avenues in a range of fields, including hydrogen evolution15,16, transistors18,19, energy storage20,21, photodetectors22, and electroluminescent devices22,23. However, there are still serious limitations related to the available band gap values. Alloying semiconductors is known to be an effective approach to achieve continuously tunable band gaps24, as reported by both theory and experiment for anion mixing in MoX2(1−x)X′2x alloys25,26. Recently, Mo1−xWxS2 monolayers have been demonstrated experimentally27,28 and it has been predicted that the band gap, hole/electron effective mass, ionization potential, and electron affinity can be engineered29.

The atomic distribution in two-dimensional crystals is particularly critical for their practical use in nano-devices. Scanning transmission electron microscopy has revealed a random structure in Mo1−xWxS2 alloys27,28. However, the samples were fabricated and characterized only at particular temperatures. It is important to know whether there exit any ordered alloys or, elsewise, what the physical origin of the random structure is. Furthermore, it is intriguing to clarify whether the possibility of alloying can be extended to other transition metal dichalcogenide monolayers. In the present work, density functional theory is combined with an empirical model and Monte Carlo simulations to systematically investigate the alloying behavior of semiconducting Mo1−xWxX2 (X = S, Se, and Te) monolayers. Ordered alloys are identified at x = 1/3 and 2/3, but appear only at low temperature due to a small energetic preference of Mo-X-W over Mo-X-Mo and W-X-W interactions.

Results

First-principles calculations are performed using the Vienna Ab-initio Simulation Package and the Perdew-Burke-Ernzerhof generalized gradient approximation30. To derive parameters for the empirical model and Monte Carlo simulations, total energies are calculated in supercells containing 6 × 6 Mo1−xWxX2 and a vacuum slab of 20 Å thickness. A cutoff energy of 500 eV and a Γ-centered 4 × 4 × 1 k-mesh are used. The calculated lattice constants of MoX2 and WX2 are identical (3.18, 3.32, and 3.55 Å for X = S, Se, and Te, respectively), consistent with previous studies31. To compare the electronic structures, √3 × √3 supercells containing zero, one, two, and three W atoms and a vacuum slab of 20 Å thickness are used with a Γ-centered 15 × 15 × 1 k-mesh. All the geometries are optimized until the residual forces remain below 0.01 eV/Å. Spin-orbit coupling is not considered, since its effect is much smaller than the variations of the band properties. The vacuum level is taken as reference point for the band edge.

The total energy (Etot) of Mo1−xWxX2 with nMo Mo and nW W atoms is approximated by an empirical model based on the sum of M-X-M interactions, given by the energies εMo-X-Mo, εMo-X-W, and εW-X-W. The numbers of appearance of these interactions are denoted as nMo-X-Mo, nMo-X-W, and nW-X-W. Then the total energy is given by

graphic file with name srep06691-m1.jpg

The first two terms are atomic reference energies (εMo and εW being the total energies of isolated Mo and W atoms, respectively), while the latter three refer to the three types of M-X-M interactions. The alloy formation energy at a W concentration of x is

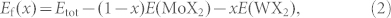graphic file with name srep06691-m2.jpg

where E(MoX2) and E(WX2) are the total energies of MoX2 and WX2 per formula unit, respectively.

For a Mo1−xWxX2 monolayer containing no W-X-W interaction the total energy depends only on x and not on the specific atomic distribution,

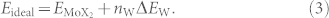graphic file with name srep06691-m3.jpg

Here 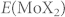Inline graphic is the total energy of a pristine MoX2 monolayer, i.e., a supercell containing 6 × 6 MoX2, and ΔEW is the energy change encountered by substituting one W atom for one Mo atom in the limit x → 0. In a random Mo1−xWxX2 alloy with n W-X-W interactions, the energy deviates from Eideal by

graphic file with name srep06691-m4.jpg

The energy gain due to the formation of one Mo-X-W interaction from Mo-X-Mo and W-X-W interactions is given by ε. According to Fig. 1, this can be expressed as

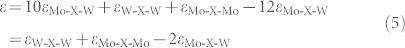graphic file with name srep06691-m5.jpg

The probability for an exchange between two configurations is determined by the Boltzmann function, depending on the temperature T and the energy difference ΔE between the two configurations,

graphic file with name srep06691-m6.jpg

When the number of W-X-W interactions changes by Δn we have

graphic file with name srep06691-m7.jpg

We employ a 60 × 60 lattice with periodic boundary conditions for various values of ε/kBT. A new atomic distribution is accepted if P exceeds a random number. This process is repeated up to 50 million times at each W concentration, which has been tested to yield the lowest energy structure.

Figure 1. Diagram illustrating the calculation of the energy gain due to the formation of Mo-X-W interactions from Mo-X-Mo and W-X-W interactions in Mo1−xWxX2.

Figure 1

Open in a new tab

Only Mo (red) and W (blue) atoms are shown. The Mo-X-W interactions are highlighted by black solid lines and the Mo-X-Mo as well as W-X-W interactions by white dashed lines.

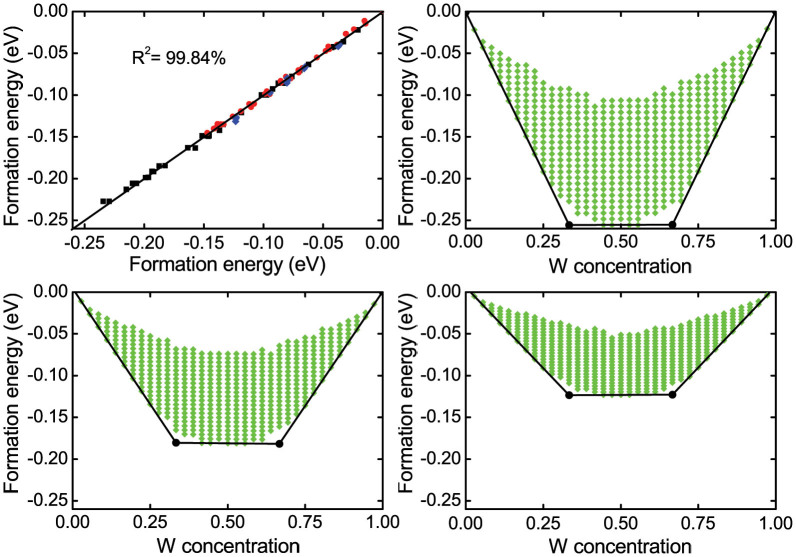
For each Mo1−xWxX2 alloy, density functional theory is used to calculate the total energies of 40 random configurations in a 6 × 6 supercell with different W concentrations between 0 and 1. Using Eq. (1) with the obtained total energies, the energy of the Mo-X-Mo, Mo-X-W, and W-X-W interactions in the empirical model are derived, see Table I. Subsequently, the total energies and corresponding formation energies of the random Mo1−xWxX2 alloys are calculated. A comparison of the alloy formation energies derived by density functional theory and the model is displayed in Fig. 2(a). The agreement is excellent, confirming that it is sufficient to consider in the model only M-X-M interactions. According to Table I, the interaction energies decrease monotonously from S to Te due to the increasing M-M distance. The energy gain, due to the formation of a Mo-X-W interaction, derived from Eq. (5), is also given in Table I. The three positive values suggest that it is energetically favorable to form Mo-X-W interactions from Mo-X-Mo and W-X-W interactions. The formation energies as a function of the W concentration show similar behaviors for X = S, Se, and Te, see Figs. 2(b)–(d), respectively. The negative values suggest that miscible alloys are formed. Two ordered alloys are obtained at x = 1/3 and 2/3, for which the number of Mo-X-W interactions is maximized (W-X-W interactions are avoided). Both show a √3 × √3 R30° superstructure, where the formation energies of the two ordered phases are the same.

Table 1. Mo-X-Mo (εMo-X-Mo), Mo-X-W (εMo-X-W), and W-X-W (εW-X-W) interaction energies derived from Eq. (1) and corresponding energy gain (ε) due to the formation of Mo-X-W interactions from Mo-X-Mo and W-X-W interactions in Mo1−xWxX2 according to Eq. (5).

  εMo-X-Mo (meV) εMo-X-W (meV) εW-X-W (meV) ε (meV)
Mo1−xWxS2 −5735.4 −6067.4 −6392.1 7.1
Mo1−xWxSe2 −5118.2 −5412.1 −5700.9 5.1
Mo1−xWxTe2 −4481.1 −4732.4 −4980.1 3.6
Open in a new tab

Figure 2.

Figure 2

Open in a new tab

(a) Comparison of the formation energies for Mo1−xWxS2 (black squares), Mo1−xWxSe2 (red dots), and Mo1−xWxTe2 (blue diamonds) between density functional theory and the empirical model described by Eq. (1). Formation energies for (b) Mo1−xWxS2, (c) Mo1−xWxSe2, and (d) Mo1−xWxTe2 as a function of the W concentration as predicted by 7 million random configurations. Black dots indicate the ordered alloys.

Total energies calculated by density functional theory are used to derive ε from Eq. (4). The almost perfectly linear dependence for the three data sets in Fig. 3(a) suggests that M-X-M interactions are sufficient to accurately describe ε. We thus consider only those in our Monte Carlo simulations. We obtain for ε values of 6.9, 5.1, and 3.5 meV for X = S, Se, and Te, respectively, which agree well with the results derived from Eq. (1). The small values can be attributed to the identical lattices of MoX2 and WX2 and the chemical similarity of Mo and W. The elongated M-M distance results in a reduction of ε, pointing to the possibility of manipulating the value by strain.

Figure 3.

Figure 3

Open in a new tab

(a) Energy deviation for Mo1−xWxS2 (black squares), Mo1−xWxSe2 (red dots), and Mo1−xWxTe2 (blue diamonds) as a function of the number of W-X-W interactions. (b) Monomer concentration as a function of the W concentration (ratio between the number of W monomers and the total number of metal atoms) at selected values of ε/kBT = 0.217, 1.25, 2.25, 2.5, 2.75, 3.25, and 7 (from bottom to top). The red line separates the random and ordered atomic distributions and the vertical blue line depicts x = 1/3. (c) W monomer/dimer concentration (ratio between the number of W monomers/dimers and the number of W atoms) as a function of the W concentration at ε/kBT = 2.75. The insets show the structures without X atoms. (d) Top view on the structure of the configuration indicated by the arrow in (c). The unit cell is marked by dashed lines.

Monte Carlo simulations are performed to explore how the atomic distribution evolves as a function of the temperature. The concentration of W monomers is defined as ratio between the number of W monomers and the total number of metal atoms. The results in Fig. 3(b) show that the W monomer concentration increases at any given x < 0.50 as the temperature decreases (ε/kBT increases). Gradually, a peak develops at x = 1/3 around ε/kBT = 2.50, suggesting that an ordered structure is formed. This is ascribed to the fact that Mo-X-W interactions are energetically favorable over Mo-X-Mo and W-X-W interactions. The corresponding phase transition temperatures are estimated to be 36, 24, and 9 K for X = S, Se, and Te, respectively. At higher temperatures, in particular at room temperature, the small ε is insufficient to maximize the number of Mo-X-W interactions. Thus, random Mo/W distributions appear, rationalizing the observations of random Mo1−xWxS2 alloys in recent experiments27,28. On the other hand, the sharp decrease of the W monomer concentration for x > 1/3 implies miscibility of the alloys. All three alloys under investigation share these properties.

Figure 3c shows the W monomer/dimer concentration (ratio between the number of W monomers/dimers and the number of W atoms) as function of x at ε/kBT = 2.75. We find that the concentration of W monomers decreases when x increases from 0 to 0.26, while the concentration of W dimers increases. However, the concentration of dimers/monomers decreases/increase from x = 0.25 to 1/3. Eventually, the monomer concentration shows a peak and the dimer concentration approaches zero at x = 1/3, suggesting an ordered configuration. In fact we find that a √3 × √3 R30° superstructure is formed, see Fig. 3(d), consistent with the model results. The curve can be understood by examining what happens when two adjacent Mo and W atoms are exchanged in a single Monte Carlo run. For small x, Δn tends to 1, giving a small probability that a new structure is accepted. Therefore, the W monomer concentration decreases. On the other hand, for x → 1/3, Δn tends to 2, see the √3 × √3 R30° configuration after exchanging two adjacent Mo and W atoms in Fig. 3(d), facilitating an ordering process. Increasing the W concentration beyond 1/3 sharply reduces the W monomer concentration, see Fig. 3(c), since every additional W atom will form W-X-W interactions. If the Mo monomer/dimer concentrations would be recorded, another √3 × √3 R30° phase would be detected, in which the Mo and W atoms are exchanged (x = 2/3; red and blue color exchanged in Fig. 3(d)).

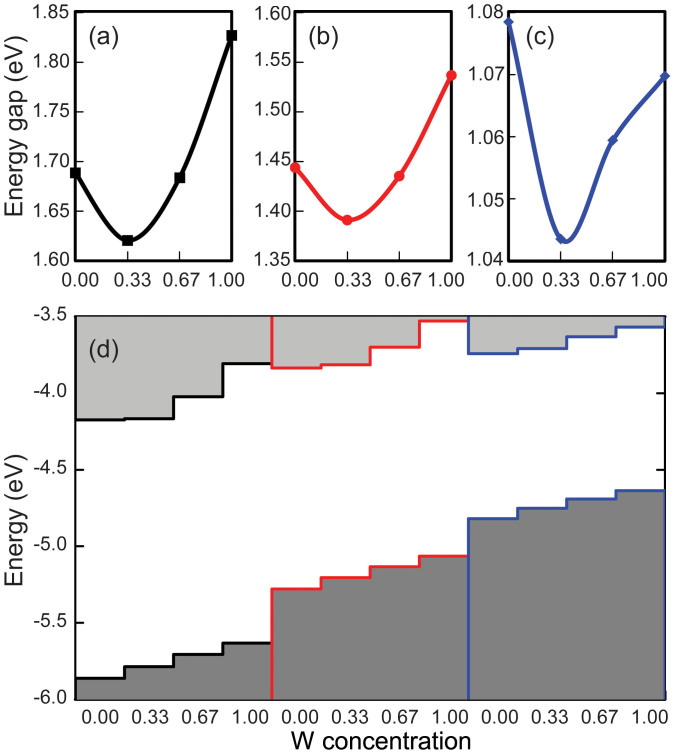
We next address the band gaps and band edges in the Mo1−xWxX2 alloys, see Fig. 4, considering only the ordered states. Note that WTe2 cannot be realized experimentally32, suggesting limitations in W doping of MoTe2. However, dilute doping should still be feasible. The band gap decreases from x = 0 to 1/3 and increases for x > 1/3, displaying a parabolic feature for both X = S and Se. The extended band gap range by alteration of the W concentration broadens the applicability of transition metal dichalcogenide monolayers in nano- and opto-electronics. Both the valence band maximum and conduction band minimum gradually shift to higher energy as x increases. Because the band edges mainly originate from metal d orbitals, the higher W 5d states result in a higher band edge. The valence band maximum shifts almost uniformly in all three alloys, whereas the conduction band minimum shifts hardly from x = 0 to 1/3 but remarkably for x > 1/3. Eventually, the magnitude of the latter shift exceeds that of the former, giving rise to a parabolic variation of the band gap. This feature can be understood by different compositions of the band edges in MoX2 and WX228,29. 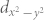Since the valence band maxima of MoX2 and WX2 originate from the metal dxy and Inline graphic orbitals, doping a W atom in MoX2 instantly shifts them up in energy. In contrast, the conduction band minimum is dominated by the metal Inline graphic states in the case of MoX2 but the dxy, Inline graphic, and Inline graphic states in the case of WX2. For x < 1/3, W contributes slightly to the conduction band minima, resulting in small energetic upshifts. For x > 1/3, the W contribution becomes dominant and thus the upshifts are enhanced. Furthermore, the M-X bond length increases from S to Te, which reduces the overlap between the M d and X p orbitals. Consequently, the magnitude of the band edge shift and of the band gap variation follows the order S > Se > Te.

Figure 4.

Figure 4

Open in a new tab

Band gap variations for (a) Mo1−xWxS2, (b) Mo1−xWxSe2, and (c) Mo1−xWxTe2 as a function of the W concentration. (d) Band alignment for the ordered states: Mo1−xWxS2 (black), Mo1−xWxSe2 (red), and Mo1−xWxTe2 (blue).

Discussion

The atomic distributions in the two-dimensional semiconducting transition metal dichalcogenide Mo1−xWxX2 (X = S, Se, and Te) alloys have been investigated by density functional theory, an empirical model, and Monte Carlo simulations. The ab-initio total energies have been used to parameterize the M-X-M interaction energies, yielding slight energetic preference of Mo-X-W over Mo-X-Mo and W-X-W interactions, which is ascribed to the identical MoX2 and WX2 lattices and the chemical similarity between Mo and W. Ordered alloys are predicted for x = 1/3 and 2/3 by the empirical model but only exist at low temperature according to the Monte Carlo simulations. At higher temperature the small energetic preference is not sufficient to maximize the number of Mo-X-W interactions, explaining the experimental observation of random Mo1−xWxS2 alloys. Negative formation energies suggest a good miscibility for all three alloys. Our results demonstrate that the band gaps and band edges can be varied continuously in Mo1−xWxX2 monolayers, with the minimal gap appearing around x = 1/3. The tunable band gap by alloying strongly broadens the range of possible applications of transition metal dichalcogenide monolayers.

Author Contributions

L.G. performed the calculations together with Q.Z., Y.Z. and Y.C.; L.G. and U.S. wrote the manuscript. All authors discussed the results and commented on the manuscript.

Acknowledgments

This work was supported by a KAUST CRG grant and computational resources were provided by KAUST HPC. Research reported in this publication was supported by the King Abdullah University of Science and Technology (KAUST).

References

  1. Lee C. et al. Frictional Characteristics of Atomically Thin Sheets. Science 328, 76–80 (2010). [DOI] [PubMed] [Google Scholar]
  2. Schwierz F. Graphene transistors. Nat. Nanotech. 5, 487–496 (2010). [DOI] [PubMed] [Google Scholar]
  3. Britnell L. et al. Field-Effect Tunneling Transistor Based on Vertical Graphene Heterostructures. Science 335, 947–950 (2012). [DOI] [PubMed] [Google Scholar]
  4. Radisavljevic B., Radenovic A., Brivio J., Giacometti V. & Kis A. Single-layer MoS2 transistors. Nat. Nanotech. 6, 147–150 (2011). [DOI] [PubMed] [Google Scholar]
  5. Zhu Z. Y., Cheng Y. C. & Schwingenschlögl U. Giant Spin-Orbit-Induced Spin Splitting in Two-Dimensional Transition-Metal Dichalcogenide Semiconductors. Phys. Rev. B 84, 153402 (2011). [Google Scholar]
  6. Xiao D., Liu G.-B., Feng W., Xu X. & Yao W. Coupled Spin and Valley Physics in Monolayers of MoS2 and Other Group-VI Dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012). [DOI] [PubMed] [Google Scholar]
  7. Johari P. & Shenoy V. B. Tuning the Electronic Properties of Semiconducting Transition Metal Dichalcogenides by Applying Mechanical Strains. ACS Nano 6, 5449–5456 (2012). [DOI] [PubMed] [Google Scholar]
  8. Hui Y. Y. et al. Exceptional Tunability of Band Energy in a Compressively Strained Trilayer MoS2 Sheet. ACS Nano 7, 7126–7131 (2013). [DOI] [PubMed] [Google Scholar]
  9. Johari P. & Shenoy V. B. Tunable Dielectric Properties of Transition Metal Dichalcogenides. ACS Nano 5, 5903–5908 (2011). [DOI] [PubMed] [Google Scholar]
  10. Yin Z. et al. Single-Layer MoS2 Phototransistors. ACS Nano 6, 74–80 (2011). [DOI] [PubMed] [Google Scholar]
  11. Mak K. F. et al. Tightly Bound Trions in Monolayer MoS2. Nat. Mater. 12, 207–211 (2013). [DOI] [PubMed] [Google Scholar]
  12. Bertolazzi S., Brivio J. & Kis A. Stretching and Breaking of Ultrathin MoS2. ACS Nano 5, 9703–9709 (2011). [DOI] [PubMed] [Google Scholar]
  13. Pu J. et al. Highly Flexible MoS2 Thin-Film Transistors with Ion Gel Dielectrics. Nano Lett. 12, 4013–4017 (2012). [DOI] [PubMed] [Google Scholar]
  14. Castellanos-Gomez A. et al. Elastic Properties of Freely Suspended MoS2 Nanosheets. Adv. Mater. 24, 772–775 (2012). [DOI] [PubMed] [Google Scholar]
  15. Lukowski M. A., Daniel A. S., Meng F., Forticaux A., Li L. et al. Enhanced Hydrogen Evolution Catalysis from Chemically Exfoliated Metallic MoS2 Nanosheets. J. Am. Chem. Soc. 135, 10274–10277 (2013). [DOI] [PubMed] [Google Scholar]
  16. Voiry D. et al. Enhanced catalytic activity in strained chemically exfoliated WS2 nanosheets for hydrogen evolution. Nat. Mater. 12, 850–855 (2013). [DOI] [PubMed] [Google Scholar]
  17. Huang X. et al. Solution-Phase Epitaxial Growth of Noble Metal Nanostructures on Dispersible Single-Layer Molybdenum Disulfide Nanosheets. Nat. Commun. 4, 1444 (2013). [DOI] [PubMed] [Google Scholar]
  18. Wang Q. H., Kalantar-Zadeh K., Kis A., Coleman J. N. & Strano M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotech. 7, 699–712 (2012). [DOI] [PubMed] [Google Scholar]
  19. Chhowalla M. et al. The Chemistry of Two-Dimensional Layered Transition Metal Dichalcogenide Nanosheets. Nat. Chem. 5, 263–275 (2013). [DOI] [PubMed] [Google Scholar]
  20. Xiao J. et al. Electrochemically Induced High Capacity Displacement Reaction of PEO/MoS2/Graphene Nanocomposites with Lithium. Adv. Funct. Mater. 21, 2840–2846 (2011). [Google Scholar]
  21. Chang K. & Chen W. In situ Synthesis of MoS2/Graphene Nanosheet Composites with Extraordinarily High Electrochemical Performance for Lithium Ion Batteries. Chem. Commun. 47, 4252–4254 (2011). [DOI] [PubMed] [Google Scholar]
  22. Splendiani A. et al. Emerging Photoluminescence in Monolayer MoS2. Nano Lett. 10, 1271–1275 (2010). [DOI] [PubMed] [Google Scholar]
  23. Mak K. F., He K., Shan J. & Heinz T. F. Control of Valley Polarization in Monolayer MoS2 by Optical Helicity. Nat. Nanotech. 7, 494–498 (2012). [DOI] [PubMed] [Google Scholar]
  24. Adachi S., Capper P., Kasap S. & Willoughby A. Properties of Semiconductor Alloys: Group-IV, III-V and II-VI Semiconductors (Wiley, Berlin, 2009). [Google Scholar]
  25. Komsa H.-P. & Krasheninnikov A. V. Two-Dimensional Transition Metal Dichalcogenide Alloys: Stability and Electronic Properties. J. Phys. Chem. Lett. 3, 3652–3656 (2012). [DOI] [PubMed] [Google Scholar]
  26. Li H. et al. Growth of Alloy MoS2xSe2(1−x) Nanosheets with Fully Tunable Chemical Compositions and Optical Properties. J. Am. Chem. Soc. 136, 3756 (2014). [DOI] [PubMed] [Google Scholar]
  27. Dumcenco D. O., Kobayashi H., Liu Z., Huang Y.-S. & Suenaga K. Visualization and Quantification of Transition Metal Atomic Mixing in Mo1−xWxS2 Single Layers. Nat. Commun. 4, 1351 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Chen Y. et al. Tunable Band Gap Photoluminescence from Atomically Thin Transition-Metal Dichalcogenide Alloys. ACS Nano 7, 4610–4616 (2013). [DOI] [PubMed] [Google Scholar]
  29. Xi J., Zhao T., Wang D. & Shuai Z. Tunable Electronic Properties of Two-Dimensional Transition Metal Dichalcogenide Alloys: A First-Principles Prediction. J. Phys. Chem. Lett. 5, 285–291 (2013). [DOI] [PubMed] [Google Scholar]
  30. Kresse G. & Hafner J. Ab Initio Molecular-Dynamics For Liquid-Metals. Phys. Rev. B 47, 558–561 (1993). [DOI] [PubMed] [Google Scholar]
  31. Kang J., Tongay S., Zhou J., Li J. B. & Wu J. Q. Band Offsets and Heterostructures of Two-Dimensional Semiconductors. Appl. Phys. Lett. 102, 012111 (2013). [Google Scholar]
  32. Mar A., Jobic S. & Ibers J. A. Metal-Metal vs Tellurium-Tellurium Bonding in WTe2 and Its Ternary Variants TaIrTe4 and NbIrTe4. J. Am. Chem. Soc. 114, 8963–8971 (1992). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES