Analysis on long-range residue-residue communication employing molecular dynamics

Abstract

We investigated the possibility of inter-residue communication of side chains in barstar, an 89 residue protein, employing mutual information theory. The normalized mutual information (NMI) of the dihedral angles of the side chains was obtained from all-atom molecular dynamics simulations. The accumulated NMI from an explicit solvent equilibrated trajectory (600-ns) with free backbone exhibits a parabola–shaped distribution over the inter–residue distances (0 ~ 36 Å): smaller at the end regimes but larger in the middle regime. This analysis, plus several other measures, does not find unusual long-range communication for free backbone in explicit solvent simulations.

INTRODUCTION

The degree to which residues in a protein have specific correlated motion is a question recently investigated by mutual information^1-3 and dynamical cross correlation map (DCCM)^4-5 methodology. For example, long-range intra-protein communication of mutual information between side chains of barstar (PDB code: 1A19)⁶ and calmodulin has recently been reported employing Monte Carlo simulation with fixed backbone and implicit solvent². Strikingly, the averaged mutual information per pair was reported to be significant at long-range for both proteins. For example, the averaged mutual information shows peaks at 6 Å and 22 Å in barstar and 6 Å and 60 Å in calmodulin.

In this communication, we employed molecular dynamics (MD) simulations of 600-ns sampling time under three conditions to sample conformations of the side chains in barstar: i) with free backbone in explicit solvent, ii) with fixed backbone in implicit solvent, and iii) with fixed backbone in explicit solvent.

MATERIALS AND METHODS

We performed simulations of the barstar (PDB code: 1A19, C82A mutant) employing the NAMD 2.8 package⁷ with the CHARMM 22 force-field⁸ for which the protein parameters incorporate the CMAP terms⁹. The TIP3P water (no. of water molecules = 8,225) model¹⁰ provided explicit solvent. Positions for Na⁺ and Cl⁻ ions were generated with a condition of 5 Å between ions employing the AUTOIONIZE module of VMD¹¹ in order to approximate 150 mM in NaCl. We performed energy minimization over 20,000 steps by the conjugate gradient method. Subsequently, the system was heated to 310 K over 60 ps. The particle mesh Ewald (PME) method¹² was used for electrostatic interactions. The damping coefficient was 5 ps⁻¹ for Langevin dynamics and the non-bonded cutoff was 12 Å, with switching at 10 Å. The simulation was performed with a 2 fs time interval. Molecular dynamics simulations in the NPT ensemble (310 K, 1 atm) in explicit solvent were performed for over 100 ps with fixed backbone. MD simulations in the NPT ensemble (10 ns) were then performed with/without fixed backbone. Constant pressure (1 atm) was maintained by the Langevin piston method¹³. Finally, the NVT ensemble simulations were performed for 620 ns without constraint on the protein. The production data (600 ns) was collected after the first 20 ns. The simulation in the implicit solvent with fixed backbone was performed in the same manner but with a dielectric constant of 78.5and employing the Generalized-Born model built in NAMD 2.8 package⁷. Mutual information is defined as

$$\mathrm{MI}(X;Y)=H\left(X\right)+H\left(Y\right)-H(X;Y)$$ (1)

where H(X), H(Y) are Shannon entropies of random variables X and Y, and H(X;Y) is the joint entropy. In this study, H(X), H(Y), and H(X;Y) are interpreted as

$$\begin{array}{cc}\hfill & H\left(X\right)=-R\sum _{x\in X}p\left(x\right)\ln p\left(x\right)\hfill \\ \hfill H(X;Y)=& -R\sum _{x\in X}\sum _{y\in Y}p(x,y)\ln p(x,y)\hfill \end{array}$$ (2)

where R is the gas constant, and x and y are the discrete states (binned dihedral angles) of the random variables X and Y (side chains of residues). The p(x) and p(y) are the associated marginal probabilities, and p(x,y) is the joint probability^1.

We obtained the normalized mutual information (NMI) for dihedral angles for the side chains of barstar, including all sp³-sp³ angles: χ₁, χ₂, χ₃, χ₄, and χ₅. The dihedral angles (−180°~180°) were distributed in 18 degree angle bins. The quantity NMI(X;Y) per angle pair (X, Y) is defined as (MI(X;Y)–ε(X;Y))/H(X;Y)¹⁴. ε(X;Y) is the expected error generated from the finite sampling for the estimation of the mutual information^1,14. For the NMI per residue pair (i, j), NMI(i;j), we divide the summed NMI(X;Y) per angle pair for available angle pairs by the number of angle pairs contributing.

RESULT AND DISCUSSION

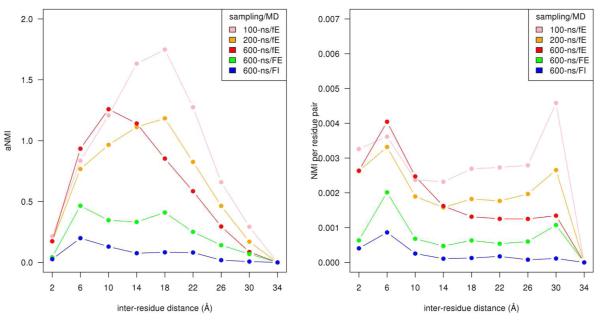
Figure 1A shows the accumulated NMI(i,j) (aNMI) from statistical sampling of a 600-ns MD simulations for several conditions. The NMI per residue pair was accumulated in 4.0 Å (C_α–C_α) distance bins. Sampling was also done for 100 and 200-ns subsets of the 600-ns MD simulation for the free backbone, explicit solvent case. The aNMI for the conventional MD (600-ns) in explicit solvent with free backbone initially increases proportional to the inter–residue distance with the maximum value ~ 10 Å and then decreases as the inter–residue distance increases. On the other hand, the aNMI for the case of implicit solvent with fixed backbone, the conditions of Ref. 2, shows two differences compared to the aNMI in explicit solvent with free backbone : i) the value of the aNMI is significantly smaller, ii) the maximum value occurs ~ 6 Å (rather than ~ 10 Å) and then generally decreases thereafter. The aNMI for the case of fixed backbone in explicit solvent fits neatly between the free backbone in explicit solvent (600-ns) and fixed backbone in implicit solvent.

Figure 1.

(A) The bin-accumulated normalized mutual information (aNMI), for three different samplings employing 600-ns MD simulations: i) free backbone in explicit solvent (red, fE), ii) fixed backbone in explicit solvent (green, FE), and iii) fixed backbone in implicit solvent (blue, FI). Also included, 100-ns (lightpink, fE) and 200-ns (orange, fE) sampling subset from the above 600-ns MD simulation (red, fE) of free backbone in explicit solvent.

(B) The NMI per residue pair in a 4 Å distance bin for the same five samplings in Figure 1A. The NMI per residue pair in each 4 Å (C_α–C_α) distance bin is summed and then divided by number of residue pairs belonging to the bin.

The aNMI for a 200-ns sampling subset of the 600-ns MD simulation in explicit solvent with free backbone (Figure 1A) has a larger value of aNMI compared to the 600-ns simulation in the intermediate and long–range regime with a maximum near 18 Å. Indeed, the aNMI for a 100-ns subset sampling has even larger values over almost the entire range: the gap between the 100-ns and 200-ns curves is larger than that between the 200-ns and 600-ns curves.

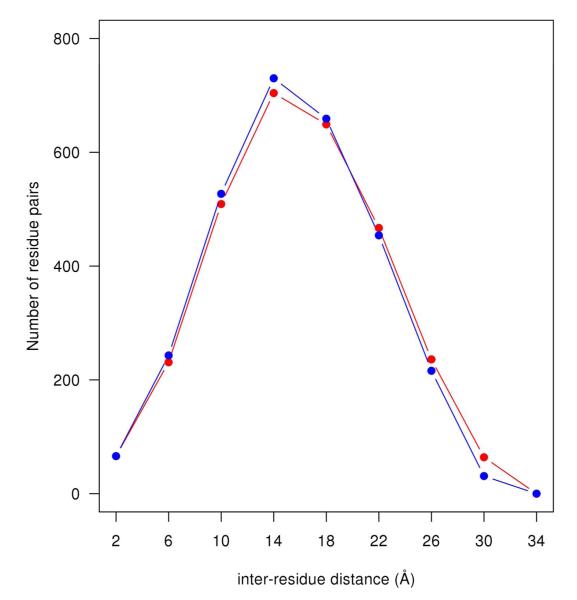
Figure 1B shows the NMI per residue pair vs. distance, i.e., for each 4 Å distance bin, the aNMI was divided by the number of residue pairs in a distance bin. A maximum occurs in the short-range regime of the inter–residue distance (~ 6 Å) for the five different sampling. Long-range peaks (of variable sizes) in the NMI per residue pair plots occur ~ 30 Å for the four different sampling cases. A partial reason for the functional difference between in Figure 1A and Figure 1B at long range apparently lies in the number of pairs in a bin. The distribution of number of pairs in a bin shows a parabolic–like shape as shown in Figure 2. (A parabolic–like shape for this distribution is also found, for instance, in a protein of larger size than barstar, cytochrome–P450 (PDB code: 2CPP) with 405 residues¹⁵ (data not shown). It is reasonable to suppose that this functional shape will be true for all globular proteins.) At the two extreme regimes (short and long-range) in the inter-residue distance, the number of pairs in a bin is relatively small (See Figure 2). Thus, the division of the aNMI (See Figure 1A) by the number of pairs in a bin contributes to a relative increase in the apparent side-chain correlations at short and long inter-residue distances, as well as relative suppression of apparent correlations at mid-range (See Figure 1B). We conclude that the NMI per residue pair in a bin may overemphasize the apparent long range order communication of mutual information relative to the aNMI, especially for the less sampled cases (100 and 200-ns). For the NMI per residue pair curve (Figure 1B), we find that the gap between the 100-ns and 200-ns sampling curves is larger than the gap between the 200-ns and 600-ns sampling curves, as was the case for the aNMI. Interestingly, the NMI perresidue pair plots (explicit solvent with free backbone or with fixed backbone) from the MD simulations (Figure 1B) show a similar pattern as compared with the result estimated from the Monte Carlo simulation² (fixed backbone, implicit solvent).

Figure 2.

Number of residue pairs in a distance bin vs. distance of barstar for the last snapshot of the 600-ns MD simulation with free backbone in explicit solvent (red, fE) and for the X-ray crystal structure (PDB code: 1A19, C82A mutant of barstar, red).

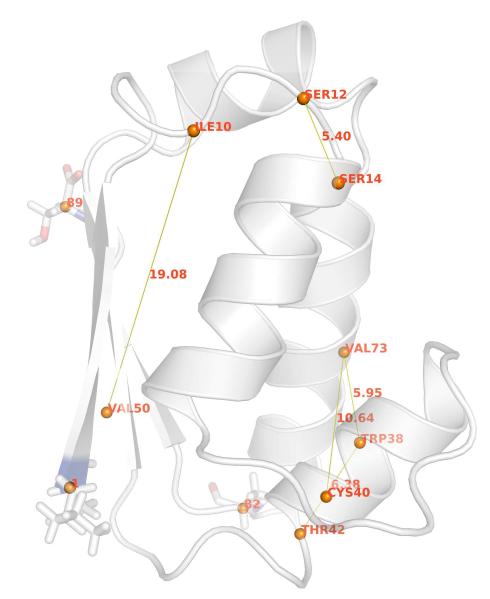
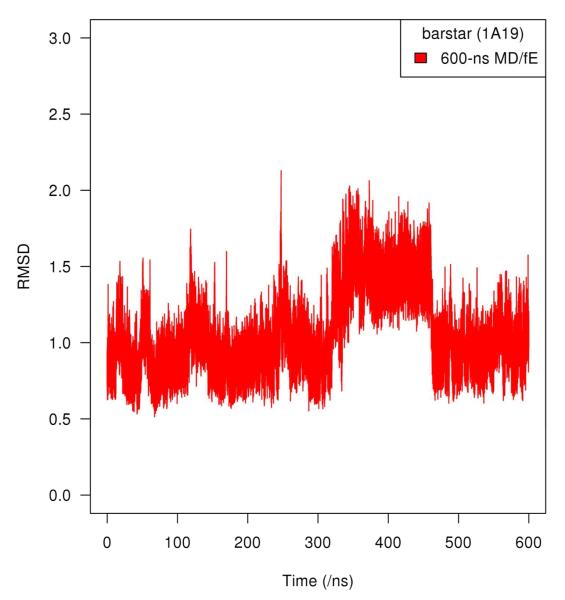
Figure 3 shows the secondary structure of the last snapshot of the 600-ns MD simulation in explicit solvent with free backbone. The five connecting lines (Figure 3) represent the five residue pairs with largest individual NMI values from the 600-ns MD simulation with free backbone in explicit solvent. The NMI values and Cα–Cα distance are listed in Table I. Among those five residue pairs shown in the Table I, three are short–range (~ 5–6 Å), one intermediate range (~ 11 Å), and one longer-range (~ 19 Å). Interestingly, the three side chains involved in the residue pairs with the five largest NMI values are also considered to be the critical residues in barnase–barstar binding: 38Trp, 42Thr and 73Val¹⁶. We find that residue 50Val is also involved in longer–range communication in both fixed backbone cases (Table 1). We also find that for the fixed backbone, explicit solvent case, longer range correlations persist at 600-ns (Table 1). The Cα–RMSD (simulation vs. X-ray crystal structure) for the 600-ns free backbone in explicit solvent case is shown in Figure 4.

Figure 3.

Barstar at the last snapshot of 600-ns MD simulation with free backbone in explicit solvent. The five lines represent residue pairs which have the five largest individual NMI per residue pair from the 600-ns MD simulation with free backbone in explicit solvent. Among the five residue pairs, three (73Val:38Trp, 42Thr:38Trp, and 12Ser:14Ser) are short-range (~ 5–6 Å), one (73Val:40Cys) intermediate range (~ 11 Å), and one (50Val:10Ile) longer-range regime (~ 19 Å). For the orientation of barstar (C82A mutant), the N-terminus and C-terminus residues are shown in stick representation, and the single mutation residue (C82A) is also shown in stick.

Table I.

Residue pairs with the five largest individual NMI per residue pair

Explicit Solvent with free Backbone (600-ns MD)
rank	NMI	Cα-Cα Distance (Å)	Residue Pair
1	0.088	10.64	40Cys:73Val
2	0.076	5.95	38Trp:73Val
3	0.059	19.08	10Ile:50Val
4	0.052	5.40	12Ser:14Ser
5	0.048	6.38	38Trp:42Thr
Explicit Solvent with Fixed Backbone (600-ns MD)
rank	NMI	Cα-Cα Distance (Å)	Residue Pair
1	0.138	16.77	16Leu:50Val
2	0.082	5.40	12Ser:14Ser
3	0.060	14.51	6Asn:50Val
4	0.055	8.87	6Asn:16Leu
5	0.032	26.00	6Asn:29Tyr
Implicit Solvent with Fixed Backbone (600-ns MD)
rank	NMI	Cα-Cα Distance (Å)	Residue Pair
1	0.051	5.40	12Ser:14Ser
2	0.028	9.19	41Leu:73Val
3	0.026	21.21	13Ile:50Val
4	0.015	19.25	13Ile:41Leu
5	0.012	5.40	12Ser:15Asp
Explicit Solvent with free Backbone (100-ns MD)
rank	NMI	Cα-Cα Distance (Å)	Residue Pair
1	0.097	15.89	50Val:80Glu
2	0.092	14.51	6Asn:50Val
3	0.092	19.08	10Ile:50Val
4	0.066	22.62	28Glu:50Val
5	0.057	19.83	6Asn:41Leu

Figure 4.

Cα-RMSD (Root Mean Square Displacement) profiles relative to the crystal structure (PDB code: 1A19, C82A mutant barstar) for 600 ns MD simulation with free backbone and explicit solvent.

The effect of sampling time on entropy evaluation for MD simulation has been previously studied with the conclusion that increasingly longer simulation time is better¹⁷. This is apparent in Figure 1B: using this figure to assess long range side chain communications, we would reach very different conclusions for 100-ns sampling vs. 600-ns sampling. On the other hand, we note that the longest range NMI per residue pair (~ 19.1 Å for 10Ile:50Val, Table 1) was already present at 100-ns for the free backbone in explicit solvent simulation.

CONCLUSIONS

We are hard-pressed to conclude that there is unusual long-range communication between side chains in barstar. For the free backbone in explicit solvent case, the accumulated NMI (Figure 1A) plot does not support this conclusion, nor does the NMI per residue pair plot (for 600-ns). The top individual NMI values (Table 1) go only to ~ 19 Å. For the fixed backbone in implicit solvent 600-ns simulation, which has much smaller aNMI and NMI per residue pair values, the same conclusions hold. Only for the case of 600-ns, fixed backbone, explicit solvent does a long-range peak (~ 30 Å) persist in the NMI vs. distance plot. The importance of increased sampling is evident in both Figure 1A and 1B.