Accelerated 3D MERGE Carotid Imaging using Compressed Sensing with a Hidden Markov Tree Model

Abstract

Purpose

To determine the potential for accelerated 3D carotid magnetic resonance imaging (MRI) using wavelet based compressed sensing (CS) with a hidden Markov tree (HMT) model.

Materials and Methods

We retrospectively applied HMT model-based CS and conventional CS to 3D carotid MRI data with 0.7 mm isotropic resolution, from six subjects with known carotid stenosis (12 carotids). We applied a wavelet-tree model learnt from a training database of carotid images to improve CS reconstruction. Quantitative endpoints such as lumen area, wall area, mean and maximum wall thickness, plaque calicification, and necrotic core area, were measured and compared using Bland-Altman analysis along with image quality.

Results

Rate-4.5 acceleration with HMT model-based CS provided image quality comparable to that of rate-3 acceleration with conventional CS and fully sampled reference reconstructions. Morphological measurements made on rate-4.5 HMT model-based CS reconstructions were in good agreement with measurements made on fully sampled reference images. There was no significant bias or correlation between mean and difference of measurements when comparing rate 4.5 HMT model-based CS with fully sampled reference images.

Conclusion

HMT model-based CS can potentially be used to accelerate clinical carotid MRI by a factor of 4.5 without impacting diagnostic quality or quantitative endpoints.

INTRODUCTION

Atherosclerosis affects more than 18 million Americans and is the underlying process leading to heart attack and stroke. More specifically, atherosclerotic disease of the carotid arteries is estimated to cause 40% of stroke producing thrombi. MRI has recently proven valuable in the diagnosis and evaluation of atherosclerosis, particularly in large vessels (e.g. carotids, aorta). MRI offers several unique capabilities such as 1) soft tissue classification, which is useful for detecting high-risk plaque components, and 2) lack of ionizing radiation, making it feasible for routine screening and for longitudinal studies. High-resolution black-blood MRI has been used for quantifying carotid plaque morphology (1-3) and optimized multi-contrast pulse sequences have been used to delineate the vessel wall and characterize plaque components (4). Recently, non-invasive MRI measurements of plaque burden are used as quantitative endpoints in clinical trials related to atherosclerosis (5).

High signal-to-noise ratio (SNR) and high spatial resolution are important for quantitative measurements from plaque imaging. Several 2D and 3D imaging techniques have been successfully applied for carotid plaque imaging. The typical carotid protocol acquires multiple 2D multislice image sets (proton-density, T1 and T2 weighted fast spin echo, and time of flight) across a 2-3 cm segment spanning the carotid bifurcation (4) and requires about 30 minutes of scan time. Additional acceleration of imaging can be used to improve SNR or resolution of carotid MR sequences and reduce motion artifacts. Scan time reduction can be achieved by interleaving multiple image slices (6-9), employing inner volume (IV) imaging (10), utilizing parallel imaging (11,12), or some combination of these. Limitations exist to each of these methods of reducing scan time. Techniques that interleave multiple slices together are susceptible to artifacts from incomplete blood suppression (13,14) whereas both IV and parallel imaging sacrifice image SNR. Such techniques may also be subject to limitations by gradient performance, RF coil geometry, and may not be applicable to all pulse sequences. Additional complementary acceleration methods that are not subject to such limitations are needed.

Compressed sensing (CS) is a relatively new technique that allows for acceleration and denoising (15,16), and is independent of the native MR techniques. CS theory indicates that if the image is compressible in a known sparsifying domain, then with only O(Klog(N/K)) measurements, where K is the sparsity level, and N is the size of the image, a sparsity-seeking algorithm can almost exactly recover the true image. Several recent studies have demonstrated the feasibility of CS in MRI (17-19). The application of CS to carotid imaging has yielded only modest (≤3) acceleration rates thus far (20), and is more fully explored in this work.

We demonstrate high acceleration by adapting the model-based CS framework developed by Baraniuk et al. (21). The proposed method leverages an anatomy specific signal model that is trained on a carotid image database. A modified recovery algorithm is used to encourage sparse solutions that comply with the learnt model while maintaining robustness of recovery. For instance, the wavelet coefficients naturally organize into a tree structure, and large coefficients of natural images will cluster along the branches of this tree (22,23). Figure 1 illustrates this tree structure in the wavelet expansion of a 2D axial carotid image.

Figure 1.

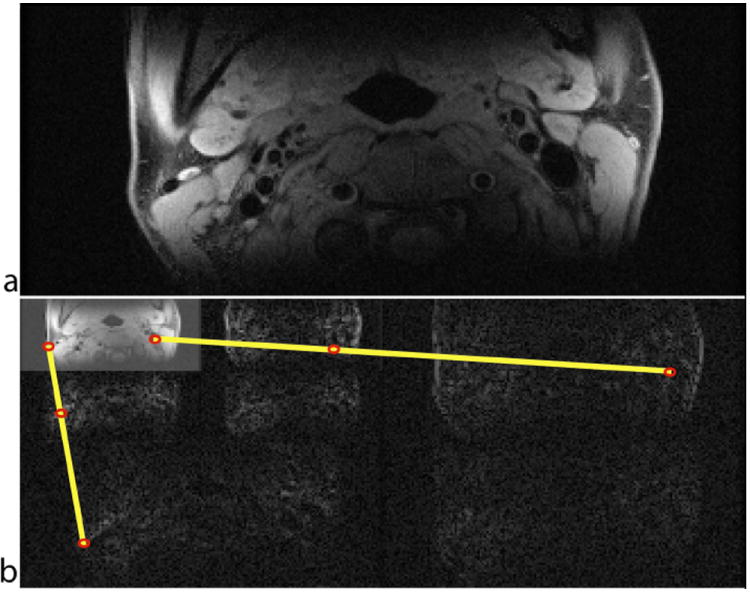
Illustration of the tree structure utilized in HMT model-based CS. (a) 2D axial image at the carotid bifurcation, and (b) its Daubechies-6 wavelet decomposition. The most significant coefficients fall along a connected tree, marked by yellow lines, with large coefficients shown in red.

MATERIALS AND METHODS

Compressed Sensing MRI

CS allows for accelerated MRI by constraining the image to conform to a known model. Classically, the MR signal can be expressed as:

$$y_i(t)=\int m(\mathrm{r})c_i(r)e^{-j2\pi \mathrm{k}(\mathrm{t})·\mathrm{r}}d\mathrm{r}$$ [1]

where y_i(t) represents the data acquired from the i^th coil, m(r) is the underlying image and c_i(r) is the receive sensitivity of the i^th coil, r is spatial position, and k(t) is spatial frequency. In discrete form, the signal equation is:

$$y_i=\mathrm{\Phi }{C}_{i}m$$ [2]

where y_i is a vector with data acquired from the i^th coil, Φ is the Fourier encoding matrix, C_i is the coil sensitivity (diagonal) matrix, and m is the discretized image. Given N basis vectors ψ_i, we can represent every possible image m ε R^N using N coefficients x_i. If we stack the vectors ψ_i into a N × N matrix Ψ, then m can be expressed as:

$$m=\mathrm{\Psi }x$$ [3]

In this sense, the image is said to be K-sparse if K < N coefficients out of N are nonzero. MR images, like most natural images, are likely to be compressible (many near-zero coefficients) but not strictly sparse. Compressible images are well approximated by K-sparse images. CS theory indicates that if the image is compressible by a known transform and if certain conditions, described below, are satisfied, then O(Klog(N/K)) measurements are sufficient to recover the true image with very high accuracy and probability (15). Assuming the MR image is compressible, the discrete MR signal equation (Eq. 2) can be re-written as:

$$y_i=A_{M}x$$ [4]

where

$$A_M={\mathrm{\Phi }}_M{C}_i\mathrm{\Psi }$$ [5]

represents the composite sensing matrix (of size M × N, where M≪N) that maps the sparse transform coefficients to the acquired data. The CS recovery theorems hold provided that A_M satisfies the ‘Restricted Isometry Property’ (RIP) (15) in addition to the sparsity/compressibility requirement. If these criteria are satisfied then the underlying image can be recovered by solving the following optimization problem:

$$\arg \underset{x}{\min }\lambda \parallel x{\parallel }_1+\parallel y-A_{M}x{\parallel }_2$$ [6]

where λ is a parameter that balances data consistency with transform sparsity. Data from each coil can also be reconstructed individually and combined after CS recovery.

Model-Based CS

Conventional CS does not make any assumptions regarding the underlying support (location) of the sparse coefficients in order to guarantee recovery for a broad variety of natural as well as artificial signals. In reality these assumptions are too general and lead to the requirement of unnecessarily inhibitive properties like the RIP. The correlations and dependencies that exist among sparse coefficient locations and values for most natural images can be exploited by using a signal model. A signal model M_K, essentially restricts the K-sparse signal x that lives in the union of arbitrary K-dimensional canonical subspaces to a much smaller subset i.e. M_K subset of (^NK). This provides a structured sparsity model that can be eventually used to reduce the dimensionality of the sparse search space.

Correlations among sparse coefficient locations and values enable us to learn statistics of significant coefficients from a training database. Then these statistics are incorporated in the recovery algorithm as a prior to effectively reduce the dimensionality of the search space without sacrificing algorithm robustness. If an appropriate model is utilized, then the required number of measurements reduces from O(Klog(N/K)) to O(K).

Wavelet Tree Model

Wavelet transforms have been used for generating sparse representations in a wide variety of applications including image compression and CS-MRI (21). The wavelet transform decomposes an image into coarse approximation coefficients, essentially a low-resolution image, and detail coefficients, which are highly sparse. This corresponds to a one-scale decomposition. The approximation coefficients can further be recursively decomposed with subsequent wavelet transforms at coarse scales, forming a tree structure. For natural images, significant wavelet coefficients do not occur at arbitrary locations but exhibit a characteristic structure (22,23). If these statistics of significant coefficients can be learnt from a training database then the resulting signal model can be incorporated at the reconstruction stage. The CS recovery algorithms can be modified to encourage solutions that comport with the learnt signal model. This provides an opportunity to flexibly trade off the search complexity during recovery with a higher acceleration rate during measurement.

In standard wavelet representation of images, nested sets of coefficients are generated at every scale of the decomposition. All coefficients at every scale (except the last) will have 4 children (in 2D image) or 8 children (in 3D image) coefficients at the next finer scale. Similarly all children coefficients will have a parent at the previous coarser scale (except the first). Coefficient magnitudes usually persist through scales due to the analysis properties of wavelet basis functions. The presence of an edge in the original image will manifest as a large wavelet coefficient while smooth regions will generally result in small wavelet coefficients. Edges will usually create a chain of large coefficients linked across scales. This phenomenon is known in the literature as the persistence property. Also the magnitudes of wavelet coefficients exponentially decay at finer scales. This causes the significant wavelet coefficients of piecewise smooth signals to concentrate within a connected subtree of the wavelet tree.

In practice, coefficients of most real images will not form perfectly connected trees (23). There are primarily three reasons for this break in structure. 1) The expected sparsity of wavelet coefficients decreases at coarser scales, since carotid MR images are superpositions of large smooth regions with contour singularities of varying sizes. 2) Since wavelet bases are frequency band filters, its coefficients close to the edges oscillate around the zero value. 3) The linearity of the wavelet transform may cause two or more edges to cancel out coefficients at coarser scales due to destructive interference. In other words, the persistence of the wavelets across scale is weaker at coarser scales. This yields a non-connected set of meaningful wavelet coefficients. Hence we must develop a carotid specific model that allows for such variations and embodies this statistical structure. These properties in spite of problems of loose connectivity of the tree induce a joint statistical structure that is still far stronger than simple sparsity or compressibility (21,23).

Hidden Markov Tree Model

Hidden Markov Tree (HMT) models succinctly and accurately represent this joint statistical structure. The key properties of wavelets that include persistence and exponential decay across scales are captured by a tree-based Markov model that correlates the states of parent and children coefficients. HMT modeling has been used successfully to improve performance of denoising (22), classification, and even reconstruction from undersampled data (23). In this work we closely follow the framework developed in 22 and 23 and apply it to MR image reconstruction. HMT models the non-Gaussian probability density function of each wavelet coefficient as a mixture of two hidden binary states. The two states are used to determine whether a particular coefficient is large or small in magnitude.

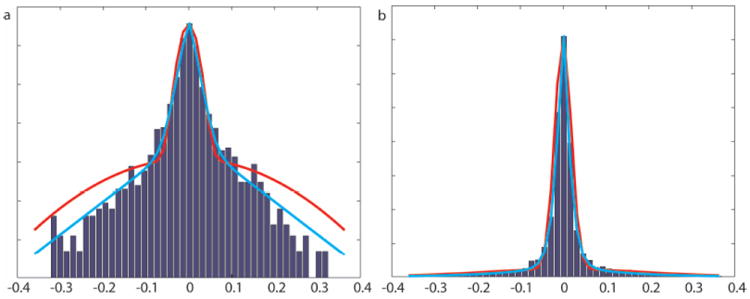
A two-component mixture of generalized Gaussians can be used to stochastically model the distribution of sparse coefficients with large and small magnitudes. In previous works (22,23) a two-component mixture of Gaussians was sufficient to model signal statistics. However, we observed that a mixture of generalized Gaussians provide a better statistical fit for wavelet coefficients of 3D MERGE carotid images (see Figure 2). Since the MR images are generally complex, we must model statistics of real and imaginary component separately. The generalized Gaussian reduces to the standard Gaussian and Laplacian (24) distribution in special cases. The component corresponding to the small state has a relatively small variance, capturing the peakiness around zero, while the component corresponding to the large state has a relatively large variance, capturing the heavy tails.

Figure 2.

(a) Log-histogram and (b) Histogram of wavelet coefficients in one subband of a representative carotid image. The red line is a mixture of two-component Gaussians fitted to the data and the blue line is the approximation from a mixture of two-component generalized Gaussians. The generalized Gaussian mixture provides a better fit than Gaussian mixture.

The persistence of wavelet coefficient magnitudes across scale is modeled by linking these hidden states across scale in a Markov tree. A state transition matrix for each link quantifies statistically the degree of persistence of large or small coefficients. The other properties of loosely connected wavelet trees can be also incorporated in the HMT model. The decay in coefficient magnitude across scales will imply that variances associated with generalized Gaussian mixture model will decay exponentially as the scale becomes finer (22,23). The weakening in persistence across scales can be modeled by appropriately changing the state transition weights for finer scales. The Markov model is then completely determined by the set of state transition weights for linking the different coefficients at different wavelet scales.

If fully sampled training images are available then maximum likelihood estimates of the mixture variances and transition matrices can be calculated using the Expectation-Maximization (EM) algorithm (25). These parameter estimates yield a good approximation of the joint density function of the wavelet coefficients and hence the actual images. Two sets of HMT parameter estimates are learnt, one for the real component and the other for the imaginary component. With the knowledge of carotid specific HMT parameters and hidden state probabilities at the coarsest wavelet scale, we can generate a distribution for any coefficient’s hidden state by the Viterbi algorithm (26).

The iterative reweighted L1 minimization (IRWL1) algorithm (27) enables a flexible implementation that allows for specific signal penalizations while retaining the favorable computational complexity of L1 norm minimizations. The IRWL1 algorithm solves a series of L1 minimization problems with an additional weighting matrix W^k which is updated after each minimization (equation 7). In the traditional IRWL1 algorithm these weights are inversely proportional to sparse coefficient magnitude. Here we utilize a weight rule proposed in 23 for the IRWL1 algorithm that integrates the HMT model to enforce the wavelet coefficient structure during CS reconstruction. Weights are applied separately to real and imaginary components.

$${\widehat{x}}^k=\arg \underset{x}{\min }\lambda \parallel W^{k}x{\parallel }_1+\parallel y-A_{M}x{\parallel }_2$$ [7]

The weighting can be summarized as: for each wavelet coefficient in the current estimate we obtain the probability that the coefficient’s hidden state is large; in the next iteration, we apply to that coefficient a weight that is inversely proportional to that probability. The goal of this weighting scheme is to penalize coefficients with large magnitudes that have low likelihood of being generated by a wavelet sparse signal; these coefficients are often the largest contributors to the reconstruction error.

The first step of proposed algorithm consists of an initial training stage in which an EM algorithm is used to estimate the values of the parameters for a representative signal; additionally, the solution for the standard L1 minimization is obtained. Subsequently, we proceed iteratively with two alternating steps: a weight update step in which the Viterbi algorithm for state probability calculations is executed for the previous solution, and a reconstruction step in which the obtained weights are used in equation 7 to obtain an updated solution. The convergence criterion for this algorithm is the same as for the IRWL1 algortihm.

Data Acquisition

All data were collected on a Philips Achieva 3T scanner with bilateral four channel carotid phased array coils. Data were collected from 6 subjects with 16-79% carotid stenosis by ultrasound. Informed consent was obtained prior to scanning under a protocol approved by our Institutional Review Boards. Subjects were asked to avoid swallowing during the scan, and scans were repeated if they were unable to do so. 3D Motion Sensitized Driven Equilibrium prepared Rapid Gradient Echo (3D-MERGE) (28) images were acquired in the coronal plane with scan parameters that provided coverage of the full extent of carotid artery visible to the coil. One hundred coronal slices with isotropic resolution of 0.7×0.7×0.7 mm³ (zero padded to 0.35×0.35×0.35 mm³) covering a 25×16 cm² FOV were acquired in a 2 minute scan. Other sequence parameters were TR-10ms, TE-5ms, flip angle 6°, Turbo factor 30, MSDE first gradient moment 1500 mTms²/m.

Image Reconstruction

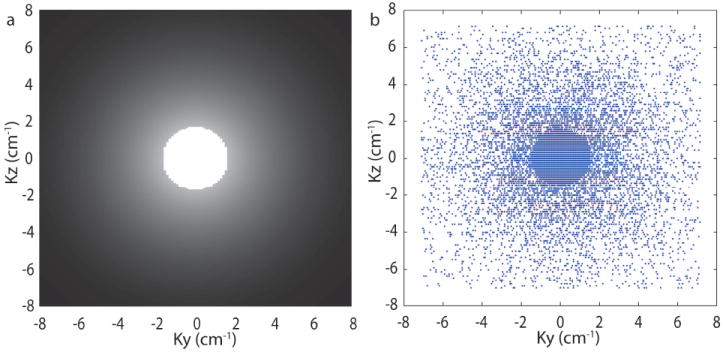
Data were retrospectively undersampled using a region of full-sampling and a region of variable density random undersampling. The sampling pattern for rate-4.5 is shown in Figure 3. Acquired data from all subjects was randomly subdivided in two disjoints sets, one for training and the other for evaluation. This process was repeated for each dataset. CS was applied to each 2D slice oriented perpendicular to the readout direction (i.e. along the two phase encoding directions, yz-plane). Two sets of images were reconstructed from each undersampled dataset, one using HMT model-based CS (21) and one using conventional L1 minimization (19). Reference images were also reconstructed from the fully sampled data using conventional Fourier reconstruction. Greedy approaches were not used because they require more data samples for equivalent image quality (29). Daubechies-6 wavelets (3-scale decomposition) are used to sparsify the images. The CS regularization parameters were chosen empirically. Computation time for training model parameters was 114 seconds using Matlab on a Linux workstation equiped with two 6-core 2.93 GHz CPUs and 48 GB of RAM. Reconstruction time for the proposed HMT model-based CS was 1900 seconds and for the standard L1 minimization was 392 seconds.

Figure 3.

(a) k-space sampling density (b) k_y-k_z phase encode locations for 4.5x undersampling.

Image Analysis

Coronal images with isotropic resolution were reformatted to the axial plane with a 2 mm slice thickness for qualitative and quantitative measurements. Image quality was visually assessed with respect to the presence of artifacts and aliasing, the conspicuity of lumen and outer wall boundaries, and conspicuity of plaque components and rated on a 4-point scale (30). The 12 carotids were randomized and stripped of patient information prior to evaluation. A radiologist viewed the reference images and images reconstructed using HMT model-based CS side by side on standard clinical picture archiving and communication system (PACS) and assigned image quality scores, on the 4-point scale. Lumen and outer wall boundaries were drawn using semiautomated plaque measurement software (31) on all slices. Morphological measurements were derived from the contours and compared between HMT model-based CS and reference images. Plaque burden measurements were averaged per artery before statistical comparison and were compared using paired Student’s t-test. Plaque burden measurements were also compared using Bland–Altman plots. A 95% confidence interval was used for all statistical tests and P-value <0.05 was considered significant.

RESULTS

Figure 4 compares HMT model-based CS with standard L1 minimization reconstructions. The images from L1 minimization are corrupted with both aliasing and wavelet basis artifacts at acceleration rate >3. At rate-4 acceleration the images from the standard approach shows significant aliasing artifacts along the undersampling direction while the HMT model-based CS reconstruction does not show any substantive artifact. The images reconstructed using HMT model-based CS suffer aliasing artifacts at rate-5. The NRMSE plots correspond to error computed only in the region covering the carotid bifurcation across all 12 carotids. HMT model-based CS reconstructions consistently yield a lower NRMSE at all acceleration rates.

Figure 4.

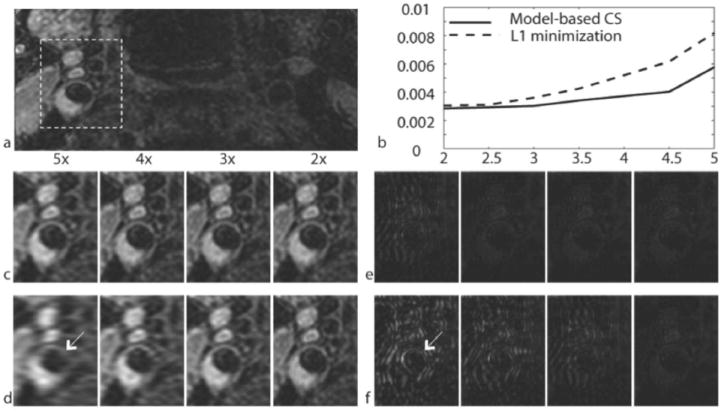
Comparison of L1 minimization and HMT model-based CS reconstructions. a) Fully sampled reference. b) Normalized RMSE (NRMSE) for CS reconstructions as a function of acceleration rate, averaged across all subjects, for an ROI containing the carotid bifurcation. c) HMT model-based CS reconstructions. d) L1 minimization reconstructions. e) Absolute difference between the HMT model-based CS and fully sampled reference. f) Absolute difference between the L1 minimization reconstructions and fully sampled reference. The arrow indicates severe artifacts in the L1 minimization difference image as compared to the HMT model-based CS difference image. All images are axial reformats. Difference images are scaled to emphasize results.

Figure 5 shows reformatted sagittal and axials slices from 5 subjects. Vessel wall images were visualized well in the sagittal plane. Axial reformats clearly depict presence of plaque and show small lesion components such has calcifications. The image reconstructed from the proposed method at 4.5 fold undersampling is almost identical to the fully sampled reference.

Figure 5.

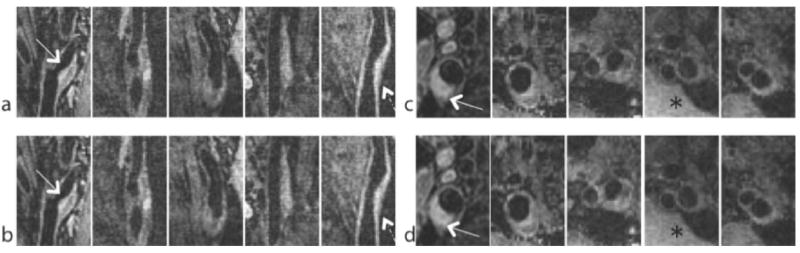
Representative sagittal and axial images from 5 carotid arteries included in this study (out of 12). Atherosclerotic plaques are marked with white arrows. (a,c) fully sampled reference. (b,d) HMT model-based CS with data undersampled by a factor of 4.5. The HMT model-based CS reconstructions have slightly lower noise level than the reference images (*), and show slight blurring of the vessel wall (dashed arrow).

The average qualitative score for reference images was 2.1 ± 0.57 while for HMT model-based CS images was 2.3 ± 0.67. Morphological measurements are summarized in Table 1. Bland–Altman plots (Fig. 6) showed no significant bias or correlation between mean and difference of measurements. The absence of bias in plaque burden measurements (Table 1 and Fig. 6) was confirmed by a paired t-test. Figure 7 shows the correlation of plaque burden measurements between reference and HMT model-based CS reconstructions. There was no significant correlation between mean values and mean differences of any plaque burden measurement for both HMT model-based CS and fully sampled reference images.

Table 1.

Paired differences between plaque morphologic measurements made on images reconstructed using HMT model-based CS (4.5x) and full sampling (1x)

	HMT CS (4.5x)	Reference (1x)	Difference	P-value
Lumen area (mm2)	19.16 ± 20.81	18.98 ± 20.54	0.17 ± 0.45	0.25
Wall area (mm2)	15.27 ± 10.76	15.54 ± 10.62	-0.27 ± 1.47	0.56
Mean wall thickness (mm)	0.86 ± 0.26	0.87 ± 0.25	-0.035 ± 0.096	0.27
Maximum wall thickness (mm)	1.37 ± 0.49	1.41 ± 0.51	-0.016 ± 0.030	0.12
Necrotic core area (mm2)	0.44 ± 0.75	0.30 ± 0.57	-0.016 ± 0.042	0.24
Calcification area (mm2)	0.48 ± 0.34	0.46 ± 0.36	0.13 ± 0.27	0.16

Figure 6.

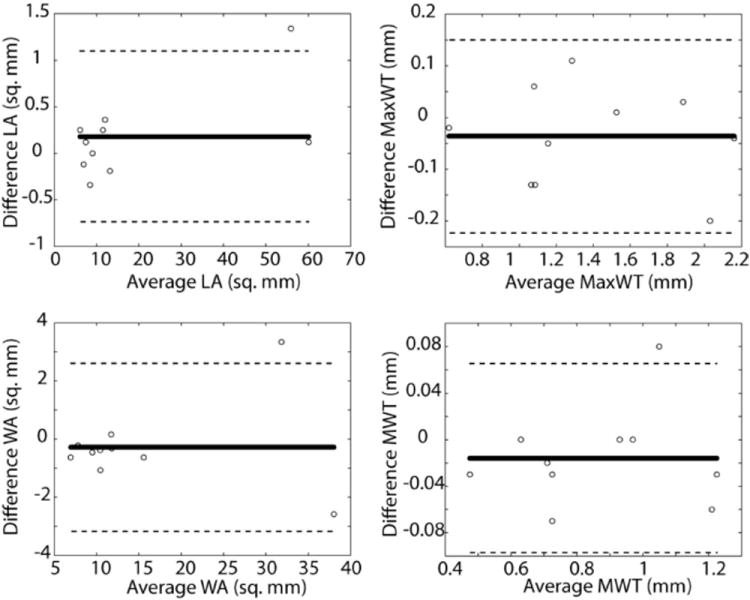
Bland–Altman plots comparing morphological measurements between HMT model-based CS reconstruction and fully sampled reference. Bold and dashed lines correspond to mean difference and limits of agreement respectively. LA, lumen area; WA, wall area; MWT, mean wall thickness; MaxWT, maximum wall thickness.

Figure 7.

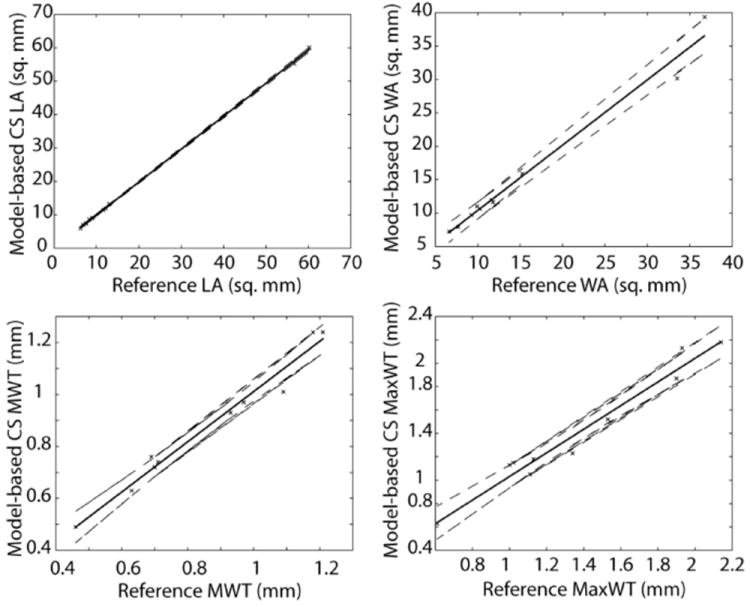
Correlation of lumen area (LA), wall area (WA), mean wall thickness (MWT) and max wall thickness (MaxWT) between reference and HMT model-based CS reconstruction. Solid and dashed lines correspond to linear regression line and 95% confidence intervals respectively.

DISCUSSION

We have demonstrated the feasibility of accelerated 3D MERGE carotid MRI using HMT model-based CS. This method exploits correlations and dependencies among transform domain coefficients in addition to the basic sparsity and compressibility required in CS. Rate-4.5 acceleration was achieved without any significant degradation in image quality or fidelity of the most informative quantitative endpoints. In addition, this work demonstrates that delineation of anatomic features that are routinely evaluated in carotid MR scans is maintained in HMT model-based CS reconstructions.

The proposed methodology is general and can be used for all forms of vessel wall imaging (VWI). VWI of thoracic aorta and peripheral arteries also yeild a similar challenge of distinguishing sharp features embedded in a dull or suppressed background. However the number of fully sampled images required for model parameter estimation and the sampling densities will need to be tuned for the different anatomies.

Recently several hybrid methods have been proposed for combing parallel imaging and CS. HMT model-based CS does not utilize coil correlations and parallel imaging theory. The proposed method can be used to replace the standard L1 minimization step in these hybrid algorithms, or multi-coil reconstruction can be directly incorporated in the proposed algorithm. However the sampling requirements for CS and parallel imaging are quite different and a new sampling density scheme will be required to maximally exploit the combination of CS and parallel imaging based acceleration.

The computational complexity of HMT model-based CS is greater than standard L1 minimization, since the proposed method solves a series of L1 minimization problems. We observed that the proposed method requires approximately 5 to 10 additional L1 minimization steps. The model parameters can be estimated efficiently using the EM algorithm and do not add significant computation cost to the reconstruction.

Reconstruction stability is impacted by fidelity of the model to the data. In this work, initial parameter training was done using the EM algorithm, which is guaranteed to converge only to a local minimum. Nevertheless we obtained reasonable estimates as long as the training data was not excessively noisy. We also found that initializing the EM algorithm with K-Means improved its convergence rate. The strength of the model mismatch penalty is controlled by a regularization parameter. We set the penalty below its optimal performance level to improve robustness. The proposed reconstruction was stable and converged to visually acceptable estimate even with noisy data.

We utilized a basic two state HMT model to capture the correlations among wavelet coefficients. Other statistical models such as Gaussian scale mixtures (32) or hierarchial Dirichlet processes (33) may better capture these dependencies and potentially allow for higher acceleration.

Since the proposed method solves successive L1 minimizations to form an estimate of sparse coefficients, the algorithm is not guaranteed to find a global minimum. Therefore, the choice of an initial guess is critical. There are several possibilities, one is to use the solution from L1 minimization. The regularization used in the initial L1 minization problem affects the final reconstruction. If a weak λ is used then the images will have ringing and aliasing artifacts. If a strong λ is used then the images will be over sparse with wavelet basis artifacts. However if the Haar wavelet is used rather than a long tap filter in the initial L1 minimization, the resultant images tend to have a benign blocking artifact. Empirically, initializations using the Haar wavelet with a strong λ produced superior reconstructions.

This study has several limitations. For instance, data from only 6 patients (12 carotids) were included. Morphological measurements were restricted to estimating area and thickness. Inclusion of a larger number of subjects, and a larger number of quantitative endpoints will be important next steps. Finally, this work has only demonstrated retrospective acceleration. Prospective studies are required to establish the full potential of this approach, including any reduction of motion artifacts, improvements in patient comfort and workflow, and potential improvements in spatial resolution.

In conclusion, we have demonstrated the application of HMT model-based CS reconstruction to 3D MERGE carotid MRI. This method exploits the connected tree structure that exists in wavelet coefficients of carotid images by permitting only certain configuration of significant coefficients and support. The proposed method provides superior reconstruction at higher acceleration factors when compared to the standard CS-MRI approach. Rate-4.5 acceleration with 3D data sets was successfully demonstrated without compromising image quality. This proposed method can be utilized for reducing scan time, improving resolution, and/or improving SNR.