Automated, contour-based tracking and analysis of cell behaviour over long time scales in environments of varying complexity and cell density

Abstract

Understanding single and collective cell motility in model environments is foundational to many current research efforts in biology and bioengineering. To elucidate subtle differences in cell behaviour despite cell-to-cell variability, we introduce an algorithm for tracking large numbers of cells for long time periods and present a set of physics-based metrics that quantify differences in cell trajectories. Our algorithm, termed automated contour-based tracking for in vitro environments (ACTIVE), was designed for adherent cell populations subject to nuclear staining or transfection. ACTIVE is distinct from existing tracking software because it accommodates both variability in image intensity and multi-cell interactions, such as divisions and occlusions. When applied to low-contrast images from live-cell experiments, ACTIVE reduced error in analysing cell occlusion events by as much as 43% compared with a benchmark-tracking program while simultaneously tracking cell divisions and resulting daughter–daughter cell relationships. The large dataset generated by ACTIVE allowed us to develop metrics that capture subtle differences between cell trajectories on different substrates. We present cell motility data for thousands of cells studied at varying densities on shape-memory-polymer-based nanotopographies and identify several quantitative differences, including an unanticipated difference between two ‘control’ substrates. We expect that ACTIVE will be immediately useful to researchers who require accurate, long-time-scale motility data for many cells.

1. Introduction

The innovative application of cell-tracking techniques in complex in vitro model environments often enables and precipitates important new insights in biology, biomedical science and biophysics. In vitro environments have recently been tailored to have specific biophysical and biochemical properties, including patterned stiffness [1], patterned surface chemistries [2] and ordered topographies [3,4]. These increasingly complex environments are now broadly employed in research on morphogenesis [5,6], cancer cell biology [7,8], cell biomechanics [9] and cell mechanobiology [10].

Although in vitro model environments have traditionally been static, recent advances in synthetic biomaterials have led to the development of environments with programmable functionality during cell culture. These in vitro environments can better mimic dynamic processes that exist in vivo, such as morphogenetic deformations [11–17] and extracellular matrix (ECM) remodelling [18–20]. For example, materials with mechanically or magnetically actuated surface topography or altered stiffness can change cell morphology [21–23] and lineage specification [24]. Recently, we [25–29] and others [30,31] developed two-dimensional substrates and three-dimensional scaffolds based on shape-memory polymers (SMPs)—a class of smart materials capable of undergoing a programmed change in shape—that can undergo programmed thermally triggered changes in topography or architecture with attached and viable cells.

Accurate and efficient tracking of cells in these and other architecturally and temporally complex environments has become increasingly challenging. Manual tracking of cells remains widely used, largely due to the reliability of the technique and the modest computational resources and operator training required [32,33]. Manual tracking is, however, time intensive and therefore typically performed only for small or sparse cell populations and/or short time scales. To overcome limitations associated with manual tracking, many semi- or fully-automated computational techniques have been developed to identify (segment) and associate (link) cells in consecutive images [34,35]. Active contour methods have been successfully used to trace cells [36,37], cellular components [38] and animals [37], in high-contrast images, but because these methods search for compartment boundaries, they are less useful in noisy, low-contrast images and situations where cells often change direction [37]. Another commonly used segmentation method is a noise threshold, in which a specific intensity value is chosen and all intensities falling below this threshold value are deemed background noise [39,40]. There is often high variability in cell fluorescence, however, which can render thresholding methods ineffective.

Tracking of cells for more than a short period of time has been found to be particularly challenging. Cell divisions (the proliferation of cells over time) can result in untracked or mislabelled cells, and the number of cell divisions is often a desirable experimental metric itself [41–43]. Cell-merging events, in which cells come into close contact with one another over multiple frames, can make it difficult to locate one or more cells in several consecutive frames, a challenge that increases in long-time-scale analyses and with high cell densities [44]. Efforts to address both issues within a single automated cell-tracking approach have been limited. Notably, Zhou and co-workers [45,46] reported efforts to employ a smart watershed segmentation approach applied to images after thresholding. However, the approach retained the challenges and limitations associated with thresholding-based segmentation—most significantly the high signal-to-noise ratio required for accurate tracking—and software employing the approach has not been disseminated. An automated cell-tracking approach that identifies cell divisions and corrects merging events in low-contrast images remains an unfulfilled need for accurate long-term tracking in complex environments.

The challenges associated with long-term tracking are amplified by the growing need to track and analyse more than a few cells at a time. Owing to the large variability observed in cell behaviour [47], it will be necessary to collect statistically large datasets detailing cell motions and develop appropriate metrics for analysing them if tracking-based research is to tease apart subtle differences in behaviour. Improved automated tracking can aid in data collection, and the field of statistical physics provides metrics that have been successfully adapted to extract patterns and characterize collective behaviours in large datasets from several types of biological systems, including bacterial colonies [48] and schools of fish [49], at large time scales [50]. If widely adopted, the adaptation and application of displacement, velocity and diffusion metrics from statistical physics could be used to standardize comparison of cell motility across studies and fields. Yet, use of these tools in tracking research has remained limited and has generally been performed in conjunction with manual tracking or semi-automated techniques [8].

Therefore, the goal of this work was to accurately and efficiently track adherent cell populations subject to nuclear staining or transfection in complex in vitro environments over sufficiently long time scales to enable statistical-physics-based analyses of cell motility. To do so, we have developed, validated and applied a new automated computational algorithm, automated contour-based tracking for in vitro environments (ACTIVE), which identifies cell nuclei of variable staining intensities in low-contrast images, segments and links the nuclei over long periods of time (large image stacks) and processes multi-cell interactions (division or merging events) that have traditionally limited the accuracy of automated systems. We applied ACTIVE to carefully quantify subtle differences in two-dimensional cell motility behaviour on various static topographies and at different cell densities, studied using adherent mouse fibroblasts stained with nuclear fluorescent dye. Using several physics-based statistical metrics, including mean-squared displacement (MSD), velocity autocorrelation and asphericity, we analysed the cell tracks and tested for motility differences in the different environments.

2. Material and methods

2.1. Cell tracking and data analysis

In this work, we developed an automated tracking algorithm designed to process an image stack of stained nuclei, accurately identify and track cells, and quantitatively analyse cell motility over long time scales (figure 1). In the algorithm, cell nuclei are first segmented using a contour-based approach (electronic supplementary material, methods 1.1), based on work pioneered by Idema and co-workers [51,52] to identify dividing cells in the Drosophila embryo. The first key innovation of ACTIVE is that cells that may be interacting with other cells (e.g. dividing or merging) are identified (tagged) by isolating contour profiles with multiple-peak intensities and classifying dual peaks (two cells) that share a parent contour (electronic supplementary material, methods 1.2 and figure S1.1). Following tagging of possible cell interactions, linking of both isolated and interacting cells is achieved through the use of a particle-tracking approach (electronic supplementary material, methods 1.3) originally developed by Crocker & Grier [53], and later modified by Gao & Kilfoil [54]. After particle tracking is complete, the second key innovation, enabled by the first, is that cells tagged as possible interactions are analysed and categorized as divisions, merging events or special cases, and cell tracks are corrected using a customized cost function (electronic supplementary material, methods 1.4–1.6 and videos V1.1 and V1.2).

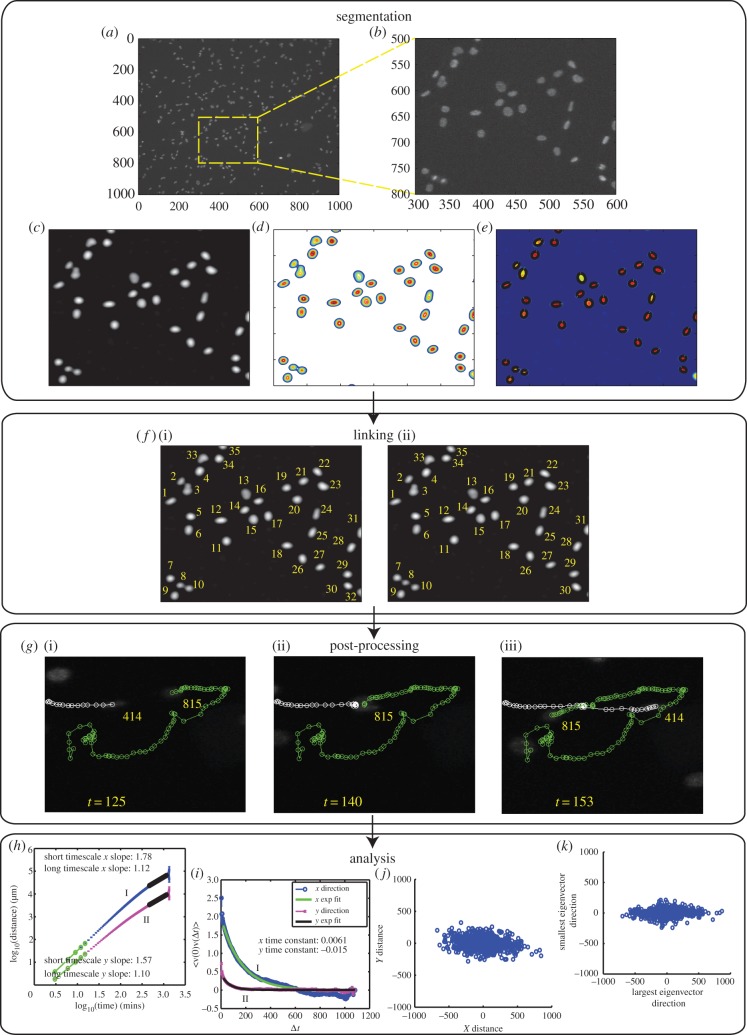
Figure 1.

Scheme depicting example segmentation, linking, interaction event post-processing and long-time-scale analyses performed by the ACTIVE automated approach. (a) Cells are stained with Hoechst 33342 dye and imaged for 24 h. (b) A highlighted image subsection illustrates varying intensities present in the nuclei of stained cells. (c) Images are initially processed using the Kilfoil bandpass filter and (d) contour profiles are established based on nuclear intensity fluctuations. (e) For single peak contours, cells are fit with a representative ellipse at half height, while multi-peak instances are tagged as two separate ellipses for division and merging event cases. (f)(i) Cell identification tags (IDs) are established and (ii) IDs are linked between consecutive frames using the Kilfoil linking system. (g)(i) Post-tracking, interaction events are identified, (ii) processed using a customized cost function and (iii) cell track information is updated for more complete and accurate complex interaction event analysis. To characterize the diffusivity and velocity dynamics of cell behaviour, cell motility behaviour is then quantified using (h) MSD (I and II for x and y data, respectively), (i) velocity-autocorrelation analyses (I and II for x and y data, respectively), (j) diffusion plots of cell tracks in which the final position for each cell was plotted after the starting location was renormalized to the plot origin and (k) final cell locations rotated by the principal axis of the gyration tensor. Images shown in the segmentation, linking, post-processing and analysis portions were all extracted from the same experimental dataset; however, referenced cells in the segmentation, linking and post-processing portions do not necessarily relate to one another unless otherwise stated above.

We also have adapted several metrics from statistical physics to quantify features of the cell tracks that ACTIVE produces. These functions, included with the ACTIVE tracking software package, calculate the MSD, velocity autocorrelation and track asphericity. MSD is defined as

2.1

where Δt is the time-interval change, r is the [x,y] distance at a specific time and N is the total number of cells [55]. To extract exponents, plots of log₁₀ MSD versus log₁₀ Δt are used. The velocity-autocorrelation function is given by

2.2

where C_v(t) is the velocity autocorrelation for a time-step t, v_i(0) is the initial velocity and v_i(t) is the velocity at time t [55]. Track asphericity was measured by first calculating the gyration tensor (S) for each cell track

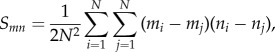2.3

where m and n refer to the Cartesian coordinates (x or y), N is the total number of track positions, and i and j are given track positions [56]. We then extracted the largest and smallest eigenvalues for the gyration tensor, 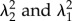, respectively, and calculated the track asphericity (A) [57–59]:

2.4

2.2. Segmentation validation

To validate the contour-based segmentation used in ACTIVE, synthetic datasets of particles—representing cell nuclei—at different densities were generated and tracked (electronic supplementary material, methods 2.1–2.2 and video V2.1). The synthetic data were only employed to test ACTIVE segmentation accuracy when compared to an accepted, established tracking technique (Kilfoil). All other analyses were performed on experimental data.

2.3. Substrate preparation

To provide new insights into cell behaviour in anisotropic environments and to benchmark ACTIVE, cell motility was studied at varying densities on highly anisotropic wrinkled substrates and on isotropic flat substrates. Anisotropic substrates of aligned micrometre-scale wrinkles were prepared as previously described [28]. Briefly, gold-coated substrates with wrinkles of 400 nm amplitude and 1 µm wavelength were fabricated to provide substrates of anisotropic topography. Flat gold-coated substrates of the same material type were fabricated to provide isotropic substrates. Flat tissue culture polystyrene (TCPS) was also used as an isotropic control.

2.4. Cell culture

For cell experiments, C3H10T1/2 mouse fibroblasts (ATCC) were seeded on wrinkled, non-wrinkled and TCPS substrates at 5000, 10 000 or 20 000 cells cm⁻² (electronic supplementary material, methods 3.1).

2.5. Cell staining and imaging

To image cell nuclei for tracking analysis, cells were stained with Hoechst 33342 nuclear dye and imaged over 24 h (electronic supplementary material, methods 3.2). Hoechst dye was added to complete growth medium at a concentration of 0.01 μg ml⁻¹. A concentration (0.01 μg ml⁻¹) significantly lower than the recommended staining concentration (0.2–2 μg ml⁻¹) was deliberately selected both to test the ability of ACTIVE to segment cells of low contrast and to ensure cell divisions throughout the 24 h time period (as Hoechst dye at the recommended concentration of 0.2 μg ml⁻¹ almost completely suppressed cell division; data not shown). At a concentration of 0.01 μg ml⁻¹ and with an image captured every 3 min with a 350 ms exposure time, cells began to apoptose after 24 h; however, further decreasing the staining concentration or the image frequency allows for longer image acquisition before cell apoptosis occurs.

2.6. Benchmarking of execution time and accuracy

ACTIVE was benchmarked by comparing execution time and accuracy to that of the Kilfoil code [54]. The Kilfoil tracking algorithm supplies a standard linking approach that is also used in ACTIVE. It is also a well-established stand-alone tracking algorithm, employing a local high-intensity-based segmentation routine distinct from the contour-based approach introduced in ACTIVE and not possessing ACTIVE's post-linkage correction for divisions, merging events and special cases. For these reasons, comparison to the Kilfoil code allowed benchmarking of both the contour-based segmentation (electronic supplementary material, methods 2.1 and 2.2 and figure S2.1) and execution time and accuracy, as follows. Using cropped image substacks (electronic supplementary material, methods 4.1), execution time for manual tracking was determined as the total time taken to manually generate tracks for all cells in all frames. Execution times for the two automated approaches, ACTIVE and the Kilfoil approach, were determined as the total time required to segment and link all cells in all frames. Occlusion accuracy was determined as the number of events that were correctly labelled divided by the total number of events that could be manually tracked with confidence (electronic supplementary material, methods 4.2).

2.7. Division detection and analysis

To assess the ability of ACTIVE to accurately detect division events, cell interaction events classified by ACTIVE as divisions were manually analysed (electronic supplementary material, methods 4.3). The accuracy of division detection was evaluated by manually determining the number of false positives—divisions flagged by ACTIVE that are not actually divisions—and the number of false negatives—divisions that occur but are not flagged by ACTIVE. The directionality of cell division was also investigated to determine the influence of substrate topography on cell divisions (electronic supplementary material, methods 7.1).

2.8. Quantification of cell motility

We quantified cell motility for varying cell densities on anisotropic and isotropic substrates using the statistical physics functions described in §2.1. This analysis was enabled by ACTIVE's ability to construct cell tracks over long time scales with high accuracy.

The MSD was calculated for each Δt and a plot of log₁₀ MSD versus log₁₀ Δt was generated for each substrate and cell density studied. Decomposition of the MSD into the x- and y-directions was also performed, with the x-direction representing the direction parallel to the wrinkle direction. Wrinkle direction was determined from phase contrast images using ImageJ (National Institutes of Health, Bethesda, MD, USA). Quantification of cell motility was achieved through comparison of MSD slopes at short and long time scales, as well as comparison of a mobility parameter, δ, which uses the intercept of a line fit to the long-time-scale MSD data to describe how fast cells displace. Diffusive migration, or migration via a ‘random walk’, generates a slope equal to unity in the log₁₀ MSD versus log₁₀ Δt plot. In these plots, superdiffustive trajectories have a slope greater than one, and ballistic migration, where cells move in a constant direction with a constant velocity, corresponds to a slope equal to two. The mobility parameter, introduced for the first time in this work, is defined as δ = 10^b, where b is the intercept of a line fit to the long-time-scale behaviour of log₁₀ MSD versus log₁₀t. With this definition, δ is equal to the square of the average cell velocity if motion is purely ballistic and equal to one-fourth of the diffusion constant if the motion is purely diffusive. For the cell motions in this work, which were found to be intermediate between ballistic and diffusive, δ is a quantitative measure of how fast cells displace. For calculation of the velocity-autocorrelation function, cell velocities were estimated using the central finite difference approximation [60], with decomposition of the velocity into x- and y-directions. For wrinkled substrates, the coordinate system was rotated so the x-direction was parallel to the wrinkles. Plots of velocity autocorrelation as a function of time were generated for each group, and each curve was fit with an exponential decay to extract a time constant, which was compared between all groups. This time constant quantifies how long a single cell tends to move in the same direction. Cell track asphericity was additionally calculated for each group, and the average asphericity for each substrate was compared. Asphericities range from 0 to 1, with a larger asphericity indicative of more directed cell migration. Cell motility was further qualitatively assessed through the construction of diffusion plots, in which the final position for each cell was plotted after the starting location was renormalized to the plot origin.

2.9. Statistics

Statistical analyses for comparison of MSD exponents, velocity autocorrelation time constants and asphericity parameters within and between substrates and densities were performed using non-parametric statistics due to deviations from the assumption of normality as revealed by Shapiro–Wilks testing. Spearman's rank correlation testing was used to evaluate the effect of density on motility parameters, and significance testing performed on the resulting correlation coefficients using a 95% confidence level. The effect of density was evaluated atop each substrate using n = 12. Kruskal–Wallis one-way analysis of variance was conducted to reveal statistical significance between substrates, followed by Wilcoxon rank-sum testing for individual comparisons. Multiple comparison testing was then performed using the Holms–Sidak correction for familywise error. Comparison of the changes in slopes as well as the difference in velocity autocorrelation time constants within groups was conducted using a paired t-test. All testing was conducted using 95% confidence levels (α value of 0.05). For each of the three substrate combinations, an n of four technical replicates was used. Therefore, substrate comparisons used n = 12, whereas for paired testing within a group n = 4.

3. Results

3.1. Results overview

The subsections that follow report the results of ACTIVE contour-based segmentation validation (§3.2), benchmarking (§3.3), cell division identification and division orientation (§3.4), cell trajectory analysis (§3.5) and quantitative MSD, velocity autocorrelation, diffusion and asphericity analyses (§3.6). In addition, detailed, multimedia results that fully illustrate the functionality and output of ACTIVE can be found in the electronic supplementary material, with the following included: synthetic data videos detailing ACTIVE segmentation (electronic supplementary material, video V2.1), along with comparisons of ACTIVE and Kilfoil accuracy results at multiple densities (electronic supplementary material, figure S2.1); cell segmentation information (electronic supplementary material, table T5.1); substrate-specific results summary tables for MSD (electronic supplementary material, table T5.2) and velocity autocorrelation and track asphericity (electronic supplementary material, table T5.3); average cell density correlation summary tables for MSD (electronic supplementary material, table T5.4) and velocity autocorrelation and cell track asphericity (electronic supplementary material, table T5.5); decomposed MSD plots for each sample (electronic supplementary material, figure S5.1), with the longer and shorter time scale decomposed slopes for each sample provided; velocity-autocorrelation plots for each sample with exponential fitting for time constant extraction (electronic supplementary material, figure S5.2); representative diffusion plots of final cell positions (electronic supplementary material, figure S5.3); plots of asphericity for each sample (electronic supplementary material, figure S5.4); density cell motility correlation behaviour summary (electronic supplementary material, figure S5.5); videos of track diffusion for the lowest density (electronic supplementary material, videos V5.1–V5.3); an example event analysed for benchmarking the accuracy of automated approaches (electronic supplementary material, video V6.1); example videos displaying correct and incorrect labelling of cell divisions (electronic supplementary material, videos V7.1–V7.3); angular spread and division orientation summary (electronic supplementary material, tables T7.1 and T7.2, and figure S7.1); and statistical analysis summaries for MSD, velocity autocorrelation and track asphericity comparisons (electronic supplementary material, tables T8.1–8.3).

3.2. Automated contour-based tracking for in vitro environment validation

When the known tracks of synthetic data were compared with those produced from ACTIVE, it was found that 97.5% of the tracks were correctly identified through the entire 480 frames of the synthetic data at low cell density, and 95.7% of the tracks were correctly identified through the entire 480 frames at high cell density (electronic supplementary material, figure S2.1). By comparison, the Kilfoil approach yielded 96.8% and 92.9% accuracy at low and high density, respectively.

3.3. Automated contour-based tracking for in vitro environment benchmarking

When benchmarked against manual tracking and the Kilfoil approach in analysis of low-contrast images from live-cell experiments, ACTIVE execution speed was comparable to that of the Kilfoil method and was two orders of magnitude faster than that of manual tracking (table 1).

Table 1.

Execution time comparison of the three tracking approaches for tracking of cells on wrinkled (stack 1) and TCPS (stack 2) substrates seeded at 10 000 cells cm⁻². The manually processed stacks have fewer tracked cells and total number of frames compared with the results presented in §§3.5–3.6.

tracking method	stack no.	no. cells identified	time for analysis (s)
manual	1	48	3600
	2	38	2040
Kilfoil	1	49	5
	2	36	4
ACTIVE	1	46	13
	2	37	12

An important feature of ACTIVE is that it allows identification of cell interaction events during segmentation (i.e. before linking). Therefore, to compare the accuracy of the two automated approaches, ACTIVE segmentation was used to identify 100 interaction events. These 100 events were then manually investigated to determine the accuracy of both automated methods during merging events (see the electronic supplementary material, video V6.1, for example) using a sample from each cell seeding density. At a low cell seeding density, ACTIVE reduced the error in identifying the appropriate cell IDs and in analysing cell–cell interactions by 43% compared with the error rate of the standard Kilfoil method (13% versus 23% error; table 2) at the expense of the observed slight decrease in execution speed (table 1). Error rates for the medium and high cell seeding densities were comparable between the two approaches.

Table 2.

Accuracy of merging event tracking for the two automated approaches. For each cell density (low = 5000 cells cm⁻², medium = 10 000 cells cm⁻² and high = 20 000 cells cm⁻²), a single representative sample was chosen, due to a wide distribution of proliferation rates sample to sample. For each sample analysed, 100 merging events were isolated and manually evaluated for accuracy. Those events identified as capable of being tracked manually with confidence were analysed to determine the accuracy of the automated approaches in event cell tracking. The selected events included cases where ACTIVE used both positional and fingerprint analysis.

seeding density	tracking method	no. events analysed	no. events correct	no. events incorrect	error (%)
low	Kilfoil	91	70	21	23
	ACTIVE	91	79	12	13
medium	Kilfoil	98	76	24	22
	ACTIVE	98	78	22	20
high	Kilfoil	89	72	28	20
	ACTIVE	89	72	28	20

3.4. Cell division identification and division orientation

To evaluate the capability of the ACTIVE approach to track cell divisions, cell events identified during segmentation as divisions were isolated and cell track videos were produced (electronic supplementary material, videos V7.1–V7.3). Division analysis was conducted for three separate densities atop a wrinkled substrate to evaluate the influence of cell density on division accuracy. For each sample, 100 events identified as divisions by ACTIVE were manually evaluated to determine the false positive rate, or how many events identified as divisions are not divisions. With increasing cell density, the false positive rate increased (table 3) due to the combination of increased number of complex cell interactions with more than two merging cells and under-segmentation resulting in the loss of cell IDs. It appears that the false positive rate increases substantially at a critical density, observed in this work as the false positive rate increased from 29 to 65% when cell seeding density increased from 10 000 to 20 000 cells cm⁻². For each sample, the number of false negatives, or divisions that ACTIVE does not identify, was also manually determined (electronic supplementary material, video V7.3) and only 15 divisions or less were missed by ACTIVE, with no apparent effect based on density.

Table 3.

Accuracy of division events as determined by false positive and false negative occurrence. For each cell density (low = 5000 cells cm⁻², medium = 10 000 cells cm⁻² and high = 20 000 cells cm⁻²), a single representative sample was chosen, due to a wide distribution of proliferation rates sample to sample. For each sample analysed, 100 division events were isolated and manually evaluated for accuracy. Those events identified by ACTIVE as being divisions that are manually determined to not be divisions contribute to the false positive rate. Separately, modified videos of the raw image sets (example shown in the electronic supplementary material, video V7.3) were manually evaluated to calculate the number of divisions not identified by ACTIVE, contributing to the false negative error.

seeding density	no. divisions identified	false positive rate (%)	no. false negatives
low	275	20	11
medium	206	29	15
high	114	65	9

Analysis of cell division revealed surface topography has an effect on the orientation of cell division. Cells on anisotropic wrinkled substrates divided parallel to the wrinkle direction, as noted by the narrow distribution in division angles (electronic supplementary material, figure S7.1) centred around 90° (wrinkle direction). Cells on the isotropic non-wrinkled and TCPS substrates showed no preferential division orientation as noted by the broad distribution in division angles (electronic supplementary material, figure S7.1). Differences in the distributions were statistically significant when comparing the anisotropic substrate to the isotropic substrates, and there were no differences in the distributions between the two isotropic groups (electronic supplementary material, tables T7.1 and T7.2).

3.5. Cell trajectory analysis

As expected, the average number of cells identified by ACTIVE increased with increasing seeding density (electronic supplementary material, table T5.1). This was coupled with a higher standard deviation of cell number for higher density experimental groups, indicating larger attachment and/or proliferation variation as seeding density increased. Qualitative analysis of cell tracks indicated that cell migratory behaviour is influenced by substrate topography (figure 2). Cells on the wrinkled substrates moved preferentially parallel to wrinkles, indicative of cell migration along the wrinkles. This behaviour was not observed on the non-wrinkled and TCPS substrates, as cell tracks showed a random orientation indicative of more random migratory behaviour.

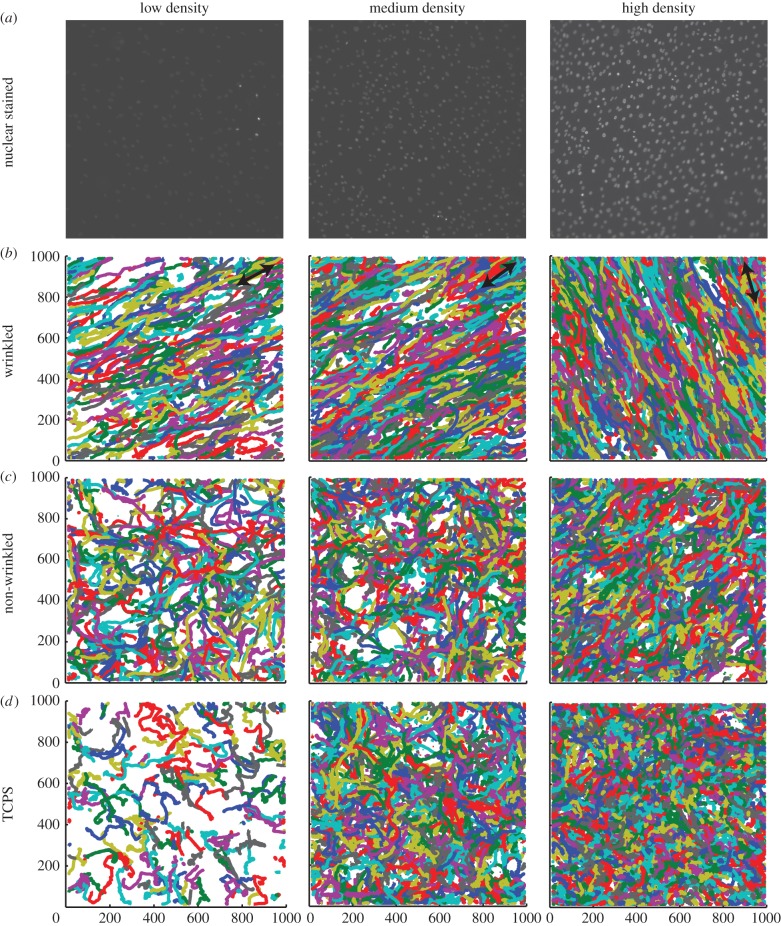
Figure 2.

Representative nuclear stained images (a) and resulting trajectory information (b–d) obtained from the ACTIVE tracking approach. Cells were stained with Hoechst 33342 nuclear dye after seeding on wrinkled, non-wrinkled or TCPS substrates. (a) Representative images for wrinkled substrates of the three seeding densities (5000, 10 000 and 20 000 cells cm⁻²) used in the anisotropy study illustrate the very low contrast used in this work. (b–d) The resulting trajectory information obtained from the ACTIVE analysis qualitatively shows that wrinkled samples yield directional migration of C3H10T1/2 mouse fibroblast cells. Representative tracks for non-wrinkled and TCPS isotropic substrates qualitatively show no preferential directional migration. For the wrinkled images, black double headed arrows indicate wrinkle direction.

3.6. Quantitative and qualitative autocorrelation analyses

Analysis of the slope of log₁₀ MSD versus log₁₀ Δt showed differences between substrates (figure 3 and electronic supplementary material, figure S5.1 and table T5.2). Wrinkled substrates exhibited a slope significantly higher than that of non-wrinkled (gold) slopes at short time scales, and TCPS substrates exhibited a slope significantly lower than both wrinkled and non-wrinkled gold-coated samples at long time scales (electronic supplementary material, table T8.1). In other words, cells move more ballistically on the wrinkled substrates.

Figure 3.

Representative MSD analyses obtained from the ACTIVE tracking results. Representative MSD plots of wrinkled, non-wrinkled and TCPS substrates with cells seeded revealed no discernible differences when comparing short- (filled black circle) and long-time-scale (empty black circle) slopes. W, wrinkled; N, non-wrinkled; T, TCPS; density = 5000 cells cm⁻²; n = 4. I and II represent decomposed x and y MSD data, respectively. (Online version in colour.)

ACTIVE also allowed the study of accurate cell tracks over longer time scales. The slope on the log₁₀–log₁₀ plots decreased significantly at the longest time scales across all substrates, indicating that cell motion becomes more diffusive. When decomposing the MSD and analysing the intercept of a line fit to the long-time-scale slope, which we have termed the mobility parameter (δ), we find significant difference between the mobility parameter for wrinkled substrates when comparing the mobility parallel (x) and perpendicular (y) to the wrinkles (electronic supplementary material, table T8.3), with higher mobility in the wrinkled direction. No significant difference between mobility parameters was observed atop the isotropic substrates (electronic supplementary material, table T8.1).

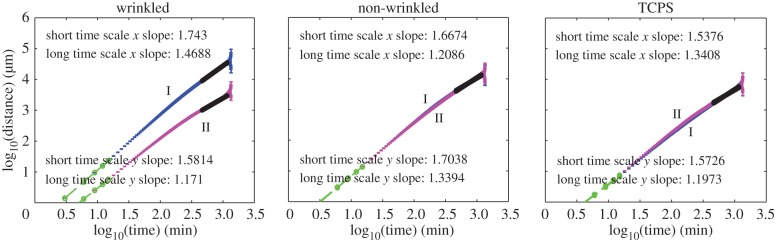
Temporal velocity-autocorrelation analysis revealed statistically significant differences between cell velocities on anisotropic and isotropic substrates (electronic supplementary material, tables T5.3 and T8.2). For the anisotropic wrinkled substrates, a statistically significant difference between the time relaxation constants for the x-velocity autocorrelation functions was observed when compared with the TCPS substrates (figure 4 and electronic supplementary material, figure S5.2). The time relaxation constant for the wrinkled samples was less than the relaxation constant for the non-wrinkled substrates, though the difference was not statistically significant.

Figure 4.

Representative velocity-autocorrelation analyses obtained from the ACTIVE tracking approach. Decomposition of x- and y-velocity (I and II, respectively) autocorrelation data reveals a distinct preferential migration of cells on wrinkled topographies corresponding to the grooved direction. The non-wrinkled and TCPS control substrates demonstrated x- and y-velocity data with similar exponential fitting for both components. Time constants for wrinkled exponential fits demonstrated statistically significant differences between x- and y-velocity component data. W, wrinkled; N, non-wrinkled; T, TCPS; density = 5000 cells cm⁻²; n = 4. (Online version in colour.)

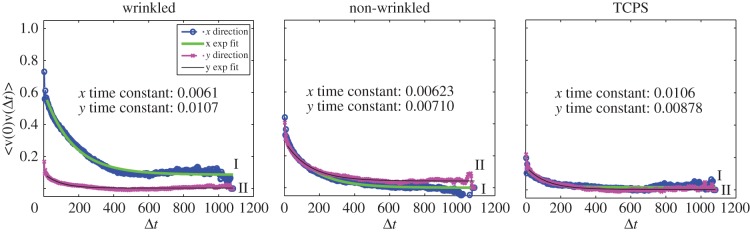
Qualitative assessment of motility behaviour was performed by generating diffusion plots for each group. After renormalization for the starting position, it was observed that cell migration on anisotropic substrates was greatest parallel to the wrinkle direction (figure 5; electronic supplementary material, videos V5.1–V5.3, and figure S5.3), as noted by the majority of final cell positions resting along the x-axis. This directed migration was not observed atop the isotropic substrates, noted by the radial distribution of final cell positions.

Figure 5.

Representative diffusion plots obtained from the ACTIVE tracking approach. Plotting the ending location for all cells with a common origin reveals distinct ‘diffusion’ patterns of cell migration between different substrates. Cells atop the wrinkled substrates preferentially migrated along the x-axis, parallel to the wrinkle direction. Atop the non-wrinkled and TCPS substrates, cells migrated in all directions as noted by the relatively uniform radial distribution of cell locations. (Online version in colour.)

Cell track asphericity revealed statistically significant differences between all substrates (electronic supplementary material, table T8.2). Track asphericities for anisotropic substrates were higher than those for both non-wrinkled and TCPS substrates (figure 6 and electronic supplementary material, figure S5.4). When rotating each cell track so the largest gyration tensor eigenvector is parallel to the x-axis, this difference is qualitatively observed (figure 6b,c). A difference between the two isotropic substrates was also observed, with cell track asphericity atop non-wrinkled substrates being significantly higher than atop TCPS substrates.

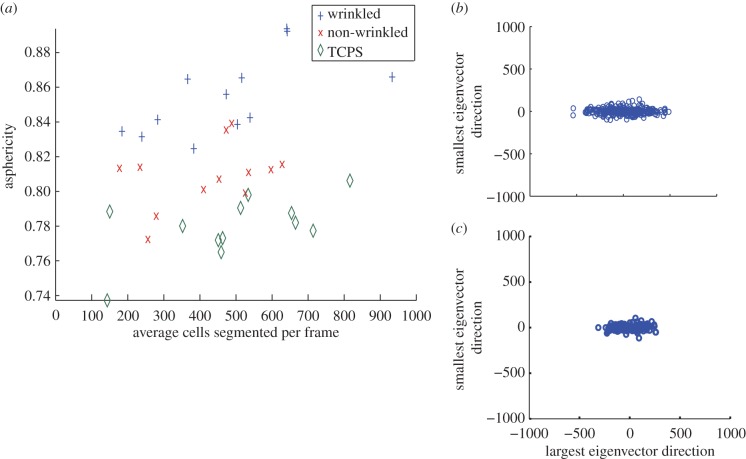
Figure 6.

Representative cell track asphericity analyses obtained from the ACTIVE tracking approach. (a) Average track asphericity as a function of average cell density (no. cells tracked) revealed a strong positive correlation atop the anisotripic wrinkled and isotropic TCPS substrates, while a weak positive correlation was observed atop the isotropic gold substrate. Asphericities atop the anisotropic wrinkled substrate were significantly higher than atop the isotropic substrates. Asphericities for cells on wrinkled (b) and flat TCPS (c) substrates can be visualized by rotating each cell track so its largest gyration tensor eigenvector (equation (2.3)) is parallel to the x-axis and plotting each cell's final rotated position. The tracks on wrinkles are more aspherical, although tracks on flat substrates still exhibit more asphericity than that expected for a random walk. (Online version in colour.)

ACTIVE also revealed significant correlation between average cell density and cell motility behaviour. Atop the isotropic substrates, a strong trend of decreasing short-time-scale slope with increasing cell density was observed (electronic supplementary material, figure S5.5 and table T5.4), whereas atop the anisotropic substrate this correlation was weak, as noted by the Spearman's rank correlation coefficients, r_s (r_s = −0.551, −0.592 and −0.189 for non-wrinkled, TCPS and wrinkled substrates, respectively). Interestingly, cell track asphericity had a strong positive correlation with cell density atop the anisotropic and isotropic TCPS substrates (r_s = 0.762 and 0.524 for wrinkled and TCPS, respectively; figure 6a and electronic supplementary material, table T5.5), but a weak positive correlation atop the isotropic gold substrate (r_s = 0.259).

4. Discussion

Despite large cell-to-cell variability, here we demonstrate statistically significant differences between motility behaviour on wrinkled and non-wrinkled substrates at cell seeding densities ranging from 5000 to 20 000 cells cm⁻². The motility differences included differences in the velocity decorrelation time and track asphericity between anisotropic and isotropic substrates, and a more surprising difference between cell track asphericity on the flat ‘control’ substrates, which have different material compositions. We also found differences in the short-time-scale motility behaviour as a function of cell density—at low densities cells move more ballistically, while at high densities they move more diffusively. These results suggest that a careful analysis of statistically large datasets generated by ACTIVE can provide new insights into how cells behave as a function of their environment.

This analysis of very large datasets was enabled by our new, automated algorithm, ACTIVE, that accurately and efficiently tracks adherent cell populations subject to nuclear staining or transfection in complex in vitro environments over sufficiently long time scales to enable statistical-physics-based analyses of cell motility. Our results indicate that the robust tracking over long time scales enabled by ACTIVE can be used to tease apart subtle differences in collective cell motility despite large cell-to-cell variability. Notably, ACTIVE analysed low-density cell–cell interactions with the error rate reduced by as much as 43% compared with the benchmark. In addition, ACTIVE simultaneously identified cell divisions and demonstrated the capability to track daughter–daughter cell relationships (functionality not present in the benchmark). Currently implemented for adherent cell populations subject to nuclear staining or transfection, the robust and flexible contour-based approach used in ACTIVE could be modified in the future for application to whole-cell staining or transfection and/or for non-adherent cells that swim or glide.

A major contribution of ACTIVE is the use of contour-based segmentation to enable detection of cell divisions and cell-merging events during segmentation and post-processing of tagged cell interactions to correct mislabelled tracks and reconnect incomplete cell tracks due to cell divisions. Inaccuracy resulting from division and merging events is a recognized challenge of automated tracking that only a few approaches have sought to address simultaneously. Jaqaman et al. [44] developed an algorithm that could link broken tracks of linearly moving particles to construct full tracks; however, the analysis did not correct for particles that may have been mislabelled. Zhou and co-workers [46] have investigated the use of smart watershedding to segment merging and dividing cells. Yet, this thresholding-based approach is unlikely to provide high accuracy results unless high signal-to-noise images are available, and it is unclear how the approach would perform for increased cell densities. ACTIVE uses contours to identify cell divisions and merging events, and the approach is effective when applied to low signal-to-noise ratio images.

At the lowest cell seeding density (5000 cells cm⁻²) we studied, ACTIVE reduced cell-merging-event-derived tracking errors by 43% compared with that of a benchmark approach (13% versus 23% error; table 2). At the higher densities studied (10 000 and 20 000 cells cm⁻²), cell-merging-event-derived tracking errors increase slightly (20% for both densities) and are comparable to that of the benchmark. These results suggest that ACTIVE is as accurate as or more accurate than alternative approaches for cell seeding densities up to 20 000 cells cm⁻². The accuracy for cell densities higher than 20 000 cells cm⁻² and for cells with motility behaviour substantially different than that of the cells studied here remains to be determined.

Importantly, further improvements in accuracy should be possible in future iterations of ACTIVE. Most of the errors observed in this work were due to higher order interactions, where more than two cells come together across several frames. An important feature of ACTIVE, absent in other tracking software, is that cell-merging and division events are identified at the segmentation stage rather than the linking stage. Therefore, ACTIVE already identifies these higher order interactions during segmentation, and future versions of the software could further improve accuracy by correcting the linking for these situations. In addition, we have implemented a hybrid manual–automated approach that identifies problematic (low confidence) multi-body interactions, displays only those events to the user and allows the user to manually link the tracks. This allows our tracking software to approach the gold standard of manual tracking, even for very complex merging events, while requiring a fraction of the user time needed for manual tracking.

In addition to accurately tracking cells in low-contrast live-cell image stacks, ACTIVE identified cell divisions and tracked daughter–daughter cell relationships, a capability often absent from cell-tracking approaches. Analysis of cell divisions also revealed an influence of surface topography on the orientation of cell division. Cells preferentially divided parallel to the wrinkles on the anisotropic substrates and showed no preferential division orientation on the isotropic substrates. From a low seeding density stack, a division accuracy of 80% was determined from manually analysing a set of 100 events classified as divisions, where 20% of the classified divisions were in fact false positives. At higher cell densities, however, this accuracy significantly drops to 30%, a limitation with the current implementation of the automated analysis. These inaccuracies can generally be attributed to complex merging events involving more than two cells (electronic supplementary material, video V7.2) and increased under-segmentation with increasing cell density. To address these inaccuracies, we have included a user-friendly graphical user interface that enables the user to manually evaluate each identified division and correct for any false positives. Manual analysis of undetected divisions identified a maximum of 15 false negatives during the 24 h live-cell image stack, highlighting the ability of ACTIVE to identify most division events.

The large, virtually complete datasets generated by ACTIVE are especially suitable for analysis using tools from statistical physics. For example, the movement of individual elements (particles or cells) can be used to calculate ensemble-averaged functions such as the MSD [61] or velocity autocorrelation. Differences in collective migration driven by gradients in mechanical properties or cell–cell interactions can be quantified using scalar quantities derived from these functions, including diffusion or time relaxation constants [62]. Finally, statistical physics metrics are particularly well suited to capture changes in the behaviour of groups of cells as a function of cell density, which could be important for understanding cell behaviour in vivo. While MSD, velocity autocorrelation and asphericity have already been included in the embodiment of ACTIVE introduced here, other types of analysis can easily be adapted and added in the future to capture additional subtle differences in cell motility. For example, pair correlation functions of the positions, orientations and velocities could be used to visualize how patterns of cell locations and orientations change with substrate and cell density [55]. In particular, we anticipate that these analyses might show signatures of ‘phase transitions’ in cell behaviours at the highest densities, where new types of collective behaviours (such as contact inhibition) occur. Other types of analyses, such as quantifying the track persistence length or modelling cell divisions as a Markov process, can also be incorporated into ACTIVE.

Analysis of cell behaviour revealed interesting similarities and differences in the motility of cells on different substrates. One surprising similarity is that the MSD of cell tracks has the same functional form as a function of time, independent of density, substrate or topography. In other words, the slopes of the MSD versus time on a log₁₀–log₁₀ plot are indistinguishable. This is very different from what is seen in non-active materials (such as colloids) as a function of density and suggests that direct cell–cell interactions (which occur more often at higher densities) do not strongly impact the trajectories of this cell type. This type of analysis requires statistically large numbers of accurate, long cell tracks, which was enabled by the ACTIVE track corrections.

This analysis identifies several different metrics that can be used to distinguish cell motility on wrinkled versus non-wrinkled substrates. We show quantitatively that cell tracks have significantly larger asphericity (anisotropy), longer velocity decorrelation times and more short-time-scale ballistic motion on wrinkled substrates compared with non-wrinkled substrates. Furthermore, we demonstrate, unsurprisingly, that the anisotropy is in the direction of the wrinkles. This agrees with previously published studies on small numbers of manually tracked cells in anisotropic environments [3,63,64], but the ACTIVE analysis included in this study achieved tracking of more than 200 times the number of cells segmented in the previous manual analysis [64]. It is anticipated that ACTIVE will facilitate this type of quantitative analysis of large cell track datasets, standardizing comparison of results across studies and fields and leading to new insights about how cell environments influence cell motility.

We also observed that cell tracks atop both of the flat substrates (gold-coated and TCPS) had asphericities much larger than that expected for a two-dimensional random walk (0.57) [59]. This is not surprising, as we know from the MSD data that our cell tracks are much more directed or ballistic than that for a random walk. Furthermore and as mentioned previously, we found that cell tracks exhibited larger asphericities atop the flat gold-coated substrates than atop the flat TCPS substrates. This subtle difference between ‘controls’ may not have been revealed if not for the accurate, complete tracks generated from the ACTIVE approach. It also suggests interesting avenues for further research. One potential explanation, based on our manual observations, is that individual cells tend to follow the track of a previous cell. Such ‘repeat’ tracks, which could be assumed to involve cell-derived matrix deposition on the substrates, might be more anisotropic, and also might occur more often on materials where cells adhere less strongly to the pristine substrate. This hypothesis could be tested with future work using ACTIVE to analyse cells atop substrates with varying adhesion strength.

Additional tracking challenges will arise as in vitro environments continue to increase in complexity. While the experiments performed in this study do not use the topography changing capability of the wrinkling system [28], this functionality could be used to study motility during dynamic changes in substrate topography. Harnessing the shape-memory effect for dynamic cell behaviour analysis is a technique that has only recently been enabled, as substrates with topography-change under cytocompatible triggering conditions have only recently been achieved. SMP substrates transitioning from isotropic to anisotropic topographies have been used to control cell alignment and cell morphology at both the micro- [25] and nanoscale [28,30]. Recently, we have extended this capability from two-dimensional substrates to three-dimemnsional scaffolds and demonstrated cell orientation to be controlled in fibre mats transitioning from an anisotropic to an isotropic architecture [29]. As topography change occurs, substrates may translate, rotate or shift out of focus, which must be minimized experimentally and accounted for during tracking. Analysis of cell motility in these environments also requires tracking of cells over longer periods of time to study the dynamic cell–material interactions on these non-equilibrium substrates. Currently, ACTIVE is equipped to handle tracking in two dimensions. However, ACTIVE could be expanded in future work to analyse motility behaviour in both two and three dimensions.

Application of ACTIVE to tracking of cells in complex in vitro environments, such as shape-changing SMPs, is anticipated to provide new insights in diverse fields. For example, it is known that breast cancer cells can exhibit mesenchymal or amoeboid motility depending on several factors, including the ECM stiffness and pore size and the ability of the cells to generate matrix metalloproteases [65]. Cells exhibiting mesenchymal motility degrade the ECM and leave behind a path that serves as a migration track for other invasive cells to follow [66]. Accurate tracking of large cell populations over long time scales may reveal important correlations of invasive cell migration, both at the individual and collective cell levels, as cells follow proteolytically generated paths. Tumour cell migration can also exhibit a mesenchymal–amoeboid transition (MAT) [67], which may be caused by changes in cell–ECM adhesion, inhibition of RHO-signalling pathways and inhibition of proteolysis [68]. SMP fibrous scaffolds capable of undergoing architecture and stiffness changes under cytocompatible conditions may serve as platforms for activating the MAT. Accurate tracking of cells through SMP scaffold change may uncover new findings about the single cell and collective MAT behaviour and whether this effect is reversible. Application of ACTIVE with SMPs may also be used to study the effects of mechanical loading of cells on wound healing. Application of mechanical forces through vacuum-assisted closure of implanted scaffolds has been shown to promote closure of skin wounds [69], where it is hypothesized that elongation of cells at the wound site enhances proliferation [70]. SMPs could be used to apply programmed strains to cells during wound-healing assays. The effect of these programmed strains on the individual and collective cell migration behaviour could be analysed with ACTIVE, potentially revealing new insights into the individual and collective cell motility responsible for improved wound healing under programmed elongation.

5. Conclusion

Quantitative, statistical-physics-based analyses of cell motility atop anisotropic and isotropic substrates revealed more diffusive (less ballistic) cell motility for increasing time scales, more persistent motility along wrinkles than perpendicular to wrinkles and a subtle difference in cell motility between our two flat ‘controls’. Our new tracking tool, termed ACTIVE, enabled this analysis of cell motility. In particular, a contour-based segmentation approach was used to enable detection of cell divisions and merging events, increasing the accuracy of cell tracks over long time scales. We expect ACTIVE to be a powerful approach for tracking adherent cell motion over long time scales in complex environments, advancing the fundamental understanding of the effect of cell–cell interactions, coupled with cell–material interactions, on cell motility. Combined with quantitative statistical metrics, this should enable new insights into cancer biology, mechanobiology and morphogenesis.

Data accessibility

Sample data and the fully functional tracking code used to generate the data presented herein are available for download at: http://henderson.syr.edu/downloads/.

Funding statement

This material is based upon work supported by the National Science Foundation under an IGERT Fellowship (DGE-1068780) to M.E.B. and Forrest Smith and under an award (CMMI-1334611) to J.H.H. and M.L.M., and by DARPA under a Young Faculty Award (D12AP00271) to J.H.H.