Part-crystalline part-liquid state and rattling-like thermal damping in materials with chemical-bond hierarchy

Significance

Materials with chemical-bond hierarchy may have a specially mixed part-crystalline part-liquid state and show nontraditional thermal transports beyond the traditional “small-parameter” lattice dynamics approach, especially the rattling-like thermal damping and thus an unusual lattice thermal conductivity that can only be described by including an effective “resonant” phonon scattering.

Abstract

Understanding thermal and phonon transport in solids has been of great importance in many disciplines such as thermoelectric materials, which usually requires an extremely low lattice thermal conductivity (LTC). By analyzing the finite-temperature structural and vibrational characteristics of typical thermoelectric compounds such as filled skutterudites and Cu₃SbSe₃, we demonstrate a concept of part-crystalline part-liquid state in the compounds with chemical-bond hierarchy, in which certain constituent species weakly bond to other part of the crystal. Such a material could intrinsically manifest the coexistence of rigid crystalline sublattices and other fluctuating noncrystalline sublattices with thermally induced large-amplitude vibrations and even flow of the group of species atoms, leading to atomic-level heterogeneity, mixed part-crystalline part-liquid structure, and thus rattling-like thermal damping due to the collective soft-mode vibrations similar to the Boson peak in amorphous materials. The observed abnormal LTC close to the amorphous limit in these materials can only be described by an effective approach that approximately treats the rattling-like damping as a “resonant” phonon scattering.

Understanding thermal and phonon transport in solids has been of great importance in many disciplines such as thermoelectrics (1–3), phononic materials (4), and thermal management composites (5). The interplay among chemical bonds, lattice dynamics, and thermal transport in materials is also an attractive topic in condensed matter physics (6) and materials science (7). Thermal transport is a key issue in thermoelectric (TE) energy-conversion materials, which are regarded among the potential candidates for revolutionizing waste-heat recovery (2, 7–9). The dimensionless figure of merit of a TE material is defined as $ZT\mathrm{=}T{S}^2\sigma /\kappa$, where T, S, σ, and κ are the absolute temperature, Seebeck coefficient, electrical conductivity, and thermal conductivity, respectively. To improve the efficiency of TE conversion, many approaches aim at reducing the thermal conductivity, especially the lattice part, to a minimum level, namely the realization of phonon-glass-like thermal transport (1, 7).

TE materials research primarily focuses on solid and crystalline thermoelectrics. It has been long viewed that all solids contain strong interatomic interactions without even an exception, and thus the established approaches to describe thermal transports in crystalline solids, including TE solids, are solely based on the perturbative “small-parameter” approximation to lattice dynamics of atoms around their equilibrium positions, i.e., phonons and phonon–phonon interactions (10, 11). As a result, crystallographic homogeneity at the atomic level in solid materials has overwhelmingly been accepted. However, recent work on exploring novel TE materials went noticeably beyond the conventional knowledge of solid TE compounds being ideally crystalline, atomically homogeneous, and dynamically perturbative. The most typical examples are filled skutterudites and clathrates with randomly rattling fillers (12–14), Cu₂Se with liquid-like fluctuating substructures (15, 16), AgSbTe₂ with extremely soft modes (17–19), SnSe with layered structures (20), etc., which show abnormal thermal transports. There is a compelling and timely need to understand their structural characteristics as well as to reveal the underlying correlations among lattice dynamics, thermal transports, and chemical bonds.

Results

Lindemann Criterion of Melting and the “Melting” Sublattice for Void Fillers.

It is well known that one way to reduce lattice thermal conductivity (LTC) is to introduce low-frequency lattice vibrations to scatter heat-carrying acoustic phonons (21–24). This has been proven a very effective approach for realizing the extremely low LTC through the randomly fluctuating rattling fillers on the void–sublattice interlocking with the rigid framework in filled skutterudites (23, 24) and clathrates (14, 25, 26). In both systems, all void fillers are individually embedded in a flattened potential energy surface due to the weak bonding or interaction with the framework (12, 13, 22, 23, 27, 28) and show ultralarge atom displacement parameters (ADPs). The ADPs are so large that the corresponding sublattice can even be considered to be “melted” based on the classical Lindemann criterion of melting (29). The Lindemann parameter δ is defined as δ = ADP^1/2/R_NN, where R_NN is the nearest-neighbor distance. Melting of a crystalline solid is usually found to occur when δ reaches 0.07 or above (29, 30). The vibration amplitude of Yb fillers in Yb_0.188Co₄Sb₁₂ from a molecular dynamics (MD) simulations at 400 K is estimated to be as large as 0.91 Å (see SI Text for details). Thus, the Lindemann parameter δ for Yb fillers is about 0.28 and far exceeds the Lindemann criterion of melting, indicating that the filler sublattice is nearly in a state of liquid. In this respect, these materials should be described as containing both a crystalline framework and noncrystalline rattling fillers with large-amplitude random movements on the void–sublattice, due to the coexistence of different types of chemical bonds of hierarchical strengths. Therefore, the whole system can hardly be regarded as a state of homogeneous crystalline solid valid for small-parameter approximation.

A Mixed Part-Crystalline Part-Liquid State in TE Materials.

The finite-temperature structural characteristics of Cu₃SbSe₃, a new type of TE material, could further demonstrate the deviation from the static and small-vibration picture. Cu–Sb–Se systems have been shown to possess a ZT value about unity (31, 32), and Cu₃SbSe₃ manifests anomalously low lattice thermal conductivity (0.7–1.0 Wm^-1⋅K⁻¹) with an unusual temperature dependence (33, 34) (see An Effective Approach for the Thermal Transport in Part-Crystalline Part-Liquid Materials) and has also been expected to possess a ZT value about unity (35). In the compound, certain type of constituent atoms weakly bond to the rest of lattice with relatively strong rigidity. For example, the Cu1 atoms in the Cu₃SbSe₃ crystal structure (SI Text), while confined in both x and y directions, can easily oscillate within a hollow channel (∼4.3 Å) in the z direction. In fact, the Cu2 atoms are also weakly bound.

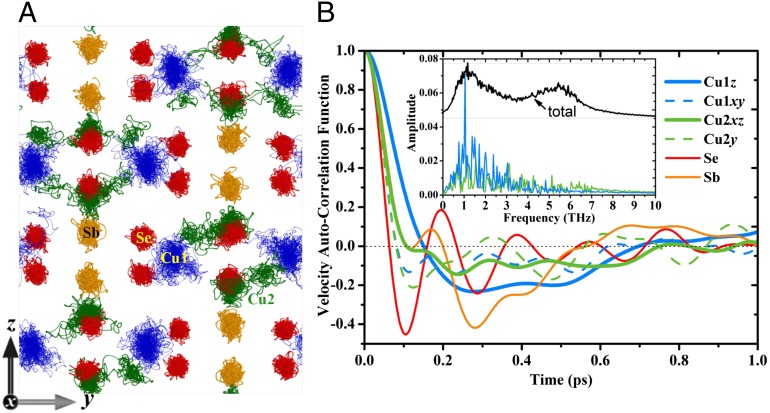
Fig. 1A plots the simulated trajectory of atoms in the y–z plane of Cu₃SbSe₃ at 400 K in MD. The oscillation amplitude for Cu atoms is more than four times larger than that for Sb or Se atoms, indicating that Cu atoms are not constrained to around their equilibrium positions. Instead, Cu atoms usually have large vibrational amplitude, and can even frequently transit to nearby sites, showing a fluid-like flow as in a partial liquid. The delocalized fluid-like flow movements of those Cu atoms are different from the large but local rattling of fillers in filled CoSb₃, and the averaged thermally induced displacement of Cu atoms in MD could be estimated to be as large as 1.54 Å, leading to a very large Lindemann parameter δ (∼0.44). In this regard, the Cu sublattice should be viewed as “sublattice melting,” and the whole system is thus in a mixed part-crystalline part-liquid state, containing a crystalline rigid part (Se and Sb sublattices) and a fluctuating noncrystalline substructure (Cu sublattice).

Fig. 1.

Results of molecular dynamics simulations. (A) Trajectory of atoms in the y–z plane from MD simulations at 400 K. (B) VAF as a function of time. (Inset) Power spectrum, evaluated by the fast Fourier transform of the VAF.

Fig. 1B plots the decay patterns of the velocity autocorrelation function (VAF) $\langle v\left(0\right)\mathrm{\cdot }v\left(t\right)\rangle$ as a function of time from MD simulations. Usually, a damped oscillating VAF reveals the strong interactions in solids, whereas for the liquid-only case one single-valley minimum is present due to the diffusive and dynamically incoherent fluctuating behavior of constituent atoms (36–38). It can be seen from Fig. 1B that the behavior of Se and Sb atoms follows a damped harmonic decay, indicating that there are strong interactions associated with them and their vibrations are very much localized. However, the projected VAFs of the Cu1z and Cu2xz exhibit a widely distributed and damped single-valley manner, representative of a nonlocal diffusion and incoherent fluctuation behavior for Cu1 in the z direction and Cu2 in the x–z planes, whereas the Cu1xy and Cu2y remain a solid-like feature with only local vibrations. Such a mixed heterogeneous feature can even be preserved at quite low temperatures based on our simulations. The Cu1z-projected phonon dispersion and phonon density of states (SI Text), by using the zero-temperature structure as input, indicate that the low-frequency vibration peaks in VAF could be primarily ascribed to the two significant peaks at around (0.8∼1.0) THz and (1.2∼1.5) THz corresponding mainly to the Cu1z-based optic phonons (SI Text). Comparing with filled CoSb₃, the intrinsic structure of Cu₃SbSe₃ manifests large vibrations and fluid-like diffusion of constituent atoms, shows even part-liquid dynamic characteristics and significant atomic-level heterogeneity, strongly deviating from the homogeneous crystalline picture of the classical solids.

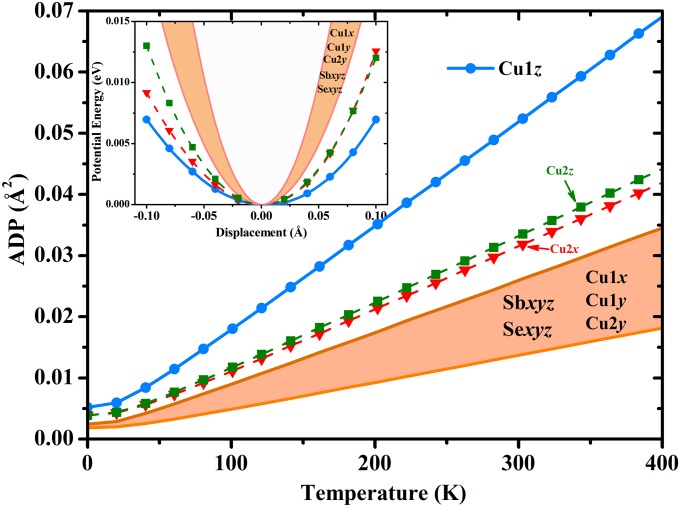
The abnormal structural and vibrational features in fact originate from the specific hierarchy of chemical bonds in the materials. By shifting the atoms away from their static equilibrium positions, we found that Cu1 atom sits in a very flat potential well and thus is only weakly bound especially in the z direction, as shown in Fig. 2, Inset. The potential well for Cu2 in the x–z directions is also very flat. However, the wells for the other species, forming relatively strong chemical bonds with the surroundings, are at least twice as steep as that for Cu1z. As a result of the bonding strength hierarchy, the ADPs for Cu atoms especially the Cu1z are very large as shown in Fig. 2. The estimated ADP for Cu1z is more than two times larger than those for other atoms (see SI Text for details). The total ADP parameters, even within a harmonic approximation, are also large, leading to a Lindemann melting parameter δ higher than 0.148 and 0.142 for Cu1 and Cu2 atoms, respectively. This is consistent with the atomic-level heterogeneity and the mixed part-crystalline part-liquid state feature due to sublattice melting given by the MD simulations.

Fig. 2.

Calculated ADPs and the corresponding atom projections for different atoms in Cu₃SbSe₃ based on phonon spectrum. The ADPs for Sb, Se, Cu2y, Cu1x, and Cu1y are within the belt region. (Inset) Calculated potential energy curves for the five nonequivalent atom types as a function of displacement about the equilibrium positions.

The Origin of Anharmonicity.

Based on the aforementioned data and analysis, LTC of Cu₃SbSe₃ is expected to show a severe reduction as well as abnormal temperature dependence, falling out of the capability of traditional model valid only for homogeneous crystalline solids. A similar phenomenon was also observed for LTC in filled skutterudites and explained as a result of nontraditional rattling-induced resonant scattering of lattice phonons (24). LTC reduction in the traditional phonon–phonon interaction picture is mainly attributed to the nonlinear scattering of acoustic phonons at elevated temperatures. In the traditional approach, the Grüneisen parameter (γ) could be adopted to describe LTC and its temperature dependence. The Umklapp (U) and normal (N) phonon scattering rates are commonly considered to be proportional to γ² according to the long-established theories (39–42). To clarify the origin of anharmonicity and its effect on LTC of Cu₃SbSe₃, the total Grüneisen parameter and partial Grüneisen parameters describing the projected contribution from given atom types and phonon branches (q, i) were all extracted from the calculated phonon dispersions. The modulus of the squared phonon polarization vector ${\left|{\mathbf{e}}_{\alpha }\left(\mathbf{q},i,\nu \right)\right|}^2$ depicts the contribution of a given atom ν in the α direction to the phonon branch i at wave vector q. Therefore, the partial Grüneisen parameter is estimated by projecting the total Grüneisen parameter γ(q, i) onto atom type µ in the α direction as follows (see SI Text for details):

$${\gamma }_{\alpha }^{\mu }\left(\mathbf{q},i\right)\mathrm{=}{\displaystyle \sum _{\nu \mathrm{\in }\mu }\gamma \left(\mathbf{q},i\right)\mathrm{\times }{\left|{\mathbf{e}}_{\alpha }\left(\mathbf{q},i,\nu \right)\right|}^2},$$ [1]

As shown in Table 1, all of the acoustic phonon branches projected onto Cu, Se, and Sb atoms possess relatively small Grüneisen parameters, indicating that intrinsic nonlinear phonon scattering of those acoustic phonons does not strongly affect LTC. Indeed, the calculated LTC from those parameters (SI Text) gives substantially higher values than the measured results, especially at relatively low temperatures (see dashed line in Fig. 3). In contrast, for the transverse optic phonon branch, the calculated partial Grüneisen parameters are relatively high, especially for Cu1 and Sb atoms. Considering the low group velocity of optic phonons, their direct contribution to LTC is rather minor. Their indirect contribution, mainly through affecting acoustic phonons based on traditional theories (43–45), is also observed to be low due to the calculated low Grüneisen parameters of the acoustic phonons. In this regard, the special vibrations associated with those optic phonons must affect thermal transports in a unique way such as producing somewhat localized vibrations or atomically heterogeneous such as the part-liquid fluctuating substructures, which makes the materials with chemical-bond hierarchy very much different from the conventional homogeneous crystalline solids. Table 1 also shows that the Cu1-related parameters are at least twice larger than those of other atoms for acoustic phonons, indicating that Cu1 plays a key role in the anharmonic scattering processes in addition to the soft-mode-related structure heterogeneity. The parameters for the Cu1 atom are overwhelmingly contributed from the z component, which is consistent with the preceding discussions about the flattest potential well and the unusually large Cu1z ADP. This indicates that crystal structural factor, such as Cu1 atoms locating near the hollow space within the crystal, contributes more to the above phenomena.

Table 1.

Grüneisen parameter and its projection

Element	${\overline{\gamma }}_{TA}$	${\overline{\gamma }}_{TA\prime }$	${\overline{\gamma }}_{LA}$	${\overline{\gamma }}_{aver}$	${\overline{\gamma }}_{TO}$
Total	1.69	1.47	1.19	1.45	3.32
Cu1	0.638	0.554	0.407	0.533	0.972
Cu1x	0.058	0.026	0.081	0.055	0.110
Cu1y	0.107	0.142	0.058	0.102	0.140
Cu1z	0.489	0.395	0.295	0.393	0.747
Cu2	0.294	0.251	0.217	0.254	0.545
Se1	0.297	0.250	0.189	0.245	0.524
Se2	0.239	0.211	0.157	0.202	0.390
Sb	0.241	0.212	0.239	0.231	0.948

The average values are only for the acoustic branches. The Grüneisen parameter of the transverse optical (TO) mode is also shown.

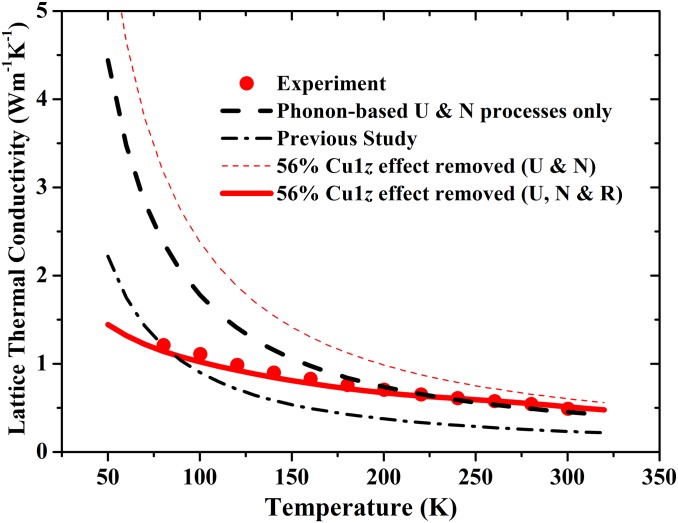
Fig. 3.

Lattice thermal conductivity of Cu₃SbSe₃. Red dots are experimental data from Skoug et al. (33). Different lines refer to theoretical results at the conditions indicated in the text.

An Effective Approach for the Thermal Transport in Part-Crystalline Part-Liquid Materials.

The above discussions strongly indicate abnormal thermal transports in Cu₃SbSe₃ as a typical compound with chemical-bond hierarchy. Indeed, a very atypical behavior of LTC including its temperature dependence was reported by Skoug et al., as shown in Fig. 3. The measured data (33) demonstrate an unusual temperature (T) dependence behavior, strongly deviating from T^-1 relationship at elevated temperatures above the Debye temperature of the compound, in addition to the extremely low LTC. These indicate that the LTC is correlated to factors more than phonon–phonon anharmonic scattering, consistent with the above discussions. By a density functional theory-based approach, we also carefully calculated the LTC of Cu₃SbSe₃ (Fig. 3), using parameters given in Table 1 and the modified Debye–Callaway model (41, 42, 46) that contains both U and N phonon scattering processes (SI Text), by assuming the dominant anharmonic phonon scattering. The calculations, as denoted in Fig. 3, strongly underestimate the LTC reduction, and even the predicted temperature-dependence tendency is also very much different from the experiments. An earlier calculation, qualitatively consistent with our theory trend, does not reproduce the measured results either (47). Considering the complex vibrational modes of Cu atoms, especially the Cu1z component, we deliberately remove part of the contribution from Cu1z to the final anharmonicity based on the percentage of harmonic term in the potential Cu1z experiences (see SI Text for details). The calculated LTC (Fig. 3) exhibits an expected T^-1 behavior, but still strongly deviates from the measured data.

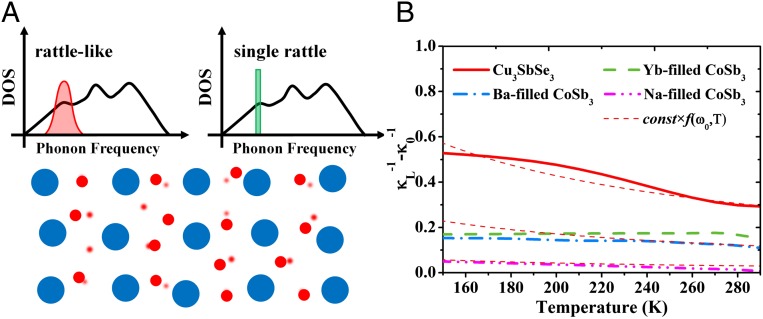
Rigorous formulation of LTC for complex systems with atomic-level heterogeneity and part-crystalline part-liquid structure, like in Cu₃SbSe₃ and filled skutterudites, is a newly raised question without any prior reference. Parallel to the LTC reduction due to the low-frequency phonon scattering by the single rattler in filled CoSb₃, we rationally infer that the abnormal lattice thermal conductivity in Cu₃SbSe₃ should also correlate with the specific large-amplitude soft-mode vibrations that give the atypical structural and lattice dynamics properties. Based on the vibrational spectrum determined from the fast Fourier transform of MD simulated VAF as given in Fig. 1B Inset, we can clearly single out a specific low-frequency vibration with a finite width. The vibration is largely from the Cu1z component (∼1.0 THz) but also contains contribution from Cu2xz. Both Cu1 and Cu2 atoms seemingly relate to the part-liquid or liquid-like structural heterogeneity in Cu₃SbSe₃ and closely link with weak chemical bonds. Comparing with the well-defined single-frequency rattling in filled CoSb₃, the low-frequency vibrations in Cu₃SbSe₃ relate to a set of atoms, coupled with each other, and thus make the phonon scattering qualitatively similar to the single-frequency rattling but cover a relatively wide frequency range due to the hierarchical distribution of different chemical bonds. Thus, this is not a single-frequency rattling but a collective broadband damped rattling or a rattle-like thermal damping. Actually, collective low-frequency vibration from a set of atoms was usually observed in amorphous or liquid materials, which originates from a certain group of atoms within relatively loosely packed regions that undergo a liquid-like motion from one configuration to another (48). The typical structure studied here is similar to the noncrystalline part-liquid substructure for atoms among the interstitial sites in the current part-crystalline part-liquid hybrid state. Recent work on the thermal transport in clathrates with static structure disorder also revealed a similar phenomenon and related that to the Boson-peak-like vibration behavior of sets of atoms in amorphous materials or structural glasses (14, 48). We also fitted experimental heat capacity to the Debye–Einstein model, and found that two Einstein oscillators of ∼0.9 THz and ∼1.6 THz have to be included to fit the measured data, implying similar lattice dynamics at both low and high temperatures (see SI Text for details).

Given phonon scattering from single rattling, the reduction of LTC can be proven to follow a universal scaling relationship (see SI Text for details),

$${\kappa }_L^{\mathrm{-}1}\mathrm{-}{\kappa }_0^{\mathrm{-}1}\mathrm{=}C\mathrm{\cdot }f\left({\omega }_0,T\right),$$ [2]

where $f\left({\omega }_0,T\right)\mathrm{=}{\omega }_0^2{\left(e^{x_0}\mathrm{-}1\right)}^2/T^3{x}_0^4{e}^{x_0}$ (${\omega }_0$ is the resonant frequency and T is the absolute temperature). ${\kappa }_0$ indicates the LTC containing only the phonon–phonon anharmonic interaction, and ${\kappa }_L$ the total or the measured result. C is a constant relating to the concentration of fillers and the effective rattling width. The scaling function is universal in theory and has been confirmed to reasonably describe the LTC reduction for filled skutterudites, as demonstrated in Fig. 4B, which plots the ${\kappa }_L^{\mathrm{-}1}\mathrm{-}{\kappa }_0^{\mathrm{-}1}$ together with scaled $f\left({\omega }_0,T\right)$ for Na-, Yb-, and Ba-filled CoSb₃.

Fig. 4.

Models for part-crystalline part-liquid materials. (A) Schematic illustration of rattling-like thermal damping (Upper Left) in materials with chemical-bond hierarchy and single-rattle phonon scattering in filled CoSb₃ (Upper Right). (Lower) Graphical rendering of part-crystalline part-liquid structure. (B) ${\kappa }_L^{\mathrm{-}1}\mathrm{-}{\kappa }_0^{\mathrm{-}1}$ and the universal scaling function $f\left({\omega }_0,T\right)$ as a function of temperature for Na-, Yb-, and Ba-filled skutterudites and Cu₃SbSe₃.

The model is also valid for the system with rattle-like phonon damping in the current Cu₃SbSe₃. At the given frequency ${\omega }_0$ (1.0 THz) from VAF calculations, the LTC reduction in Cu₃SbSe₃ follows the scaling function, indicating the validity and capability of the current model for the systems with effective rattle-like thermal damping (Fig. 4A). In this respect, the above scaling analysis indicates that the total LTC of Cu₃SbSe₃ can be described by the revised Debye–Callaway model as long as an extra rattling-like phonon scattering, ${\tau }_R^{\mathrm{-}1}\mathrm{=}{C}^{\mathrm{\ast }}{\omega }^2/\left({\left({\omega }_0^2\mathrm{-}{\omega }^2\right)}^2\mathrm{+}{\mathrm{\Delta }}^2\right)$, is introduced into the phonon relaxation rate (49). The calculated LTC including the effective rattling-like damping term is plotted in Fig. 3, showing an excellent agreement with the experiment over a wide temperature range. The formula thus becomes similar to the earlier single-rattling phonon scattering model, but the width Δ should have a physically meaningful value now. It is very likely that such a model provides an effective description for thermal transport in all part-crystalline part-liquid materials.

Conclusions

In summary, in the materials with chemical bond hierarchy, a few constituent species atoms weakly bond to the rest of the lattice with relatively strong rigidity, resulting in low-frequency vibrations and thus thermally induced large atomic displacement parameters and even fluid-like flow of atoms. As a result, such materials could intrinsically manifest the coexistence of rigid crystalline sublattices and fluctuating noncrystalline substructures, leading to atomic-level dynamic heterogeneity, mixed part-crystalline part-liquid state, rattling-like thermal damping, and thus LTC close to the amorphous limit like in a “phonon glass.” Analysis reveals the correlation among the LTC reduction, collective low-frequency vibrations similar to amorphous materials, and a universal scaling relationship, and finally leads to an effective approach in describing the thermal transport in part-crystalline part-liquid materials. This quantitatively explains the reduction of LTC, and also demonstrates the theoretical challenge of correctly describing phonon and thermal transports in complex materials. As a prediction, compounds with chemical-bond hierarchy are very likely to trigger the interest in materials with unique atomic-level dynamic heterogeneity. These materials possess extremely low LTC and can be candidates for high-performance TEs.

Methods

Our calculations were performed using the plane wave basis Vienna ab initio simulation package (VASP) code (50), implementing the generalized gradient approximation (GGA) of Perdew-Burke-Ernzerhof form (51). The interaction between ions and electrons is described by the projector augmented wave (PAW) method (52), with plane waves up to a cutoff energy of 800 eV. The configurations Cu 3d¹⁰ 4s¹, Sb 5s²5p³, and Se 4s²4p⁴ were treated as valence electrons. The Brillouin-zone integrations were performed on the grid of Monkhorst–Pack procedure. For the unit cell (28 atoms) and supercell (112 atoms), 4 × 3 × 4 and 2 × 2 × 2 k-point meshes were used, respectively. MD calculations were performed using the GGA of PBE form as implemented in the VASP code with the canonical ensemble. The PAW method is adopted, and a supercell with 259 atoms (18.25 Å × 18.25 Å × 18.25 Å) was used for Yb-filled CoSb₃. For Cu₃SbSe₃, a supercell with 112 atoms (16.20 Å × 10.67 Å × 13.87 Å) was used. The simulation temperature was set to be 400 K for two compounds, and simulation time is longer than 20 ps. The velocity autocorrelation function was found to be well converged within 20 ps.

The sample was prepared by a combination of melting–annealing and spark plasma sintering (SPS) methods. The mixture of elemental constituents was sealed in a quartz tube and melted at 1,173 K for 24 h before annealing at 673 K for 120 h. The densification of Cu₃SbSe₃ was accomplished by SPS method at 700 K for 5 min. Low-temperature heat capacity was measured from 2 K to 328 K using a Quantum Design Physical Property Measurement System.