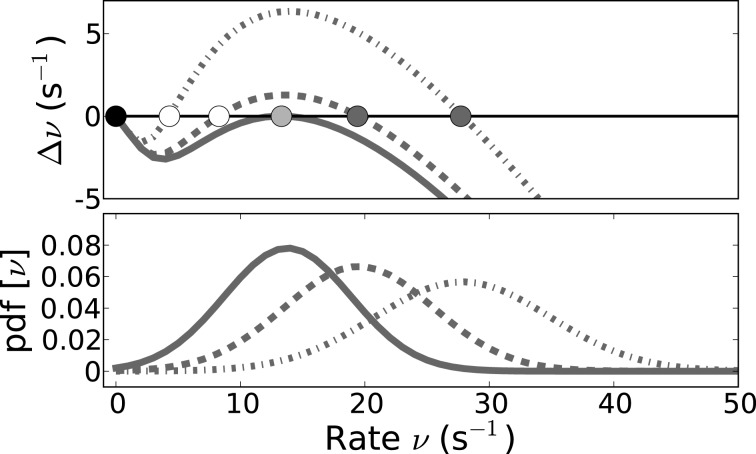
Figure 9.

The lifetime of SSAI states is determined by the size of population fluctuations vs. the size of basin of attraction. The upper panel shows the emergence of the saddle-node bifurcation that underlies the SSAI state (coalescence point for critical coupling strength J_c depicted in light gray), while the lower panel shows the population rate distributions for neurons that are driven by uncorrelated Poisson inputs, for three different values of J each (derived from Equation (23) by translating the counts to rates and approximating the binomial by a Gaussian, solid lines: J = J_c = 0.641 mV, dashed J = 0.651 mV, dashed-dotted J = 0.731 mV). In the upper panel the stable high-rate fixed-points for J > J_c are marked by dark gray, the unstable intermediate fixed-point by white circles. The black circle indicates the trivial zero-rate fixed-point. In the SSAI state the system constantly produces large population fluctuations that can drive the system substantially far away from the high-rate fixed-point. We expect the system to become stable to this inherently generated fluctuations when the basin of attraction (here the distance between the unstable and stable fixed-point) becomes larger than the characteristic size of the fluctuations, given by the variance of the population rate distribution. Parameters as in Figure 5.