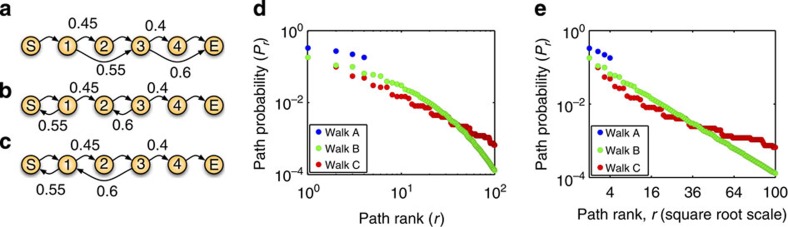
Figure 1. The path distribution for a random walk on a network may be finite, stretched exponential or power law.

(a–c) Graphical depiction of three different random walks on networks, all having the same set of nodes and transitions probabilities, but with some arcs having different endpoints. Arcs without numbers are probablity-one transitions. (d) A log–log plot of the probabilities of different paths from S to E, under the walks shown in a–c, where P_r denotes the probability of the r^th most probable path from S to E. Walk A allows only four possible paths from S to E, so its distribution is finite. For walk C, the approximate linearity of P_r with r on the log–log plot suggests that the path distribution is power law. The curvature of the points for walk B is inconsistent with a power law path probability distribution. (e) When log probabilities are plotted against the square root of rank, the points for walk B are approximately collinear, indicating a stretched exponential path probability distribution.