Massive Thermal Acceleration of the Emergence of Primordial Chemistry, the Incidence of Spontaneous Mutation, and the Evolution of Enzymes

Abstract

Kelvin considered it unlikely that sufficient time had elapsed on the earth for life to have reached its present level of complexity. In the warm surroundings in which life first appeared, however, elevated temperatures would have reduced the kinetic barriers to reaction. Recent experiments disclose the profound extent to which very slow reactions are accelerated by elevated temperatures, collapsing the time that would have been required for early events in primordial chemistry before the advent of enzymes. If a primitive enzyme, like model catalysts and most modern enzymes, accelerated a reaction by lowering its enthalpy of activation, then the rate enhancement that it produced would have increased automatically as the environment cooled, quite apart from any improvements in catalytic activity that arose from mutation and natural selection. The chemical events responsible for spontaneous mutation are also highly sensitive to temperature, furnishing an independent mechanism for accelerating evolution.

Rates of Nonenzymatic Reactions

Enzymes allow certain reactions to take place take place rapidly as compared with other reactions that confer no selective benefit upon the host organism. Once a substrate is bound, its transformation often transpires in a few milliseconds. In the absence of enzymes, the same reaction takes place relatively slowly, with a half-life that may span many hours, days, or years. Some biological reactions may be slower still in the absence of enzymes. The individual bonds connecting the components of cellulose and other polymers, readily attacked by water in the presence of enzymes, are apparently capable of long term survival in their absence to judge from the survival of submerged Viking ships and paper documents on the S. S. Titanic. If those bonds were not kinetically stable, then proteins, nucleic acids, and polysaccharides would disintegrate too rapidly to be useful for storing energy and maintaining structure and genetic information in the water that surrounds these molecules in living organisms. To appreciate what evolution has accomplished, it would be desirable to know the actual rates at which biological reactions take place in the absence of enzymes.

There are more practical reasons for wishing to know the extent to which enzymes enhance reaction rates. The remarkable selectivity of each enzyme for its preferred substrate, as well as its ability to increase the rate of reaction, is believed to depend on a distinguishing property of catalysts that was first recognized by Michael Polanyi in 1921. To enhance the rate of a reaction, the affinity of a catalyst for its substrate must increase, in passing from the ground state to the transition state. The magnitude of that increase matches the factor by which the enzyme enhances the rate of reaction (Fig. 1) (1). Accordingly, a stable molecule that resembles the altered substrate of an enzyme in the transition state would be expected to be a strong reversible inhibitor, competing with substrates for a place on the enzyme. That principle has provided a useful basis for the design of powerful enzyme inhibitors that include several drugs now used to control hypertension and the spread of HIV, and have been used as haptens to elicit the production of antibodies with catalytic activity. Transition state analogues also furnish a probe that structural biologists can use to unveil the details of the chemical mechanism of action of an enzyme and the changes in enzyme structure that almost invariably accompany catalysis (2). To estimate the minimal binding affinity expected of an ideal transition state analogue inhibitor that perfectly resembles the altered substrate in the transition state, it is necessary to compare the rate of reaction of the enzyme-substrate complex with the rate of the uncatalyzed reaction in water. If one enzyme produces a 100-fold greater rate enhancement than another enzyme, then the first enzyme should show a proportionally higher affinity for a transition state analogue inhibitor. Thus, uncatalyzed reaction rates are expected to be useful in prioritizing enzymes according to their expected sensitivity as targets for drug design.

FIGURE 1.

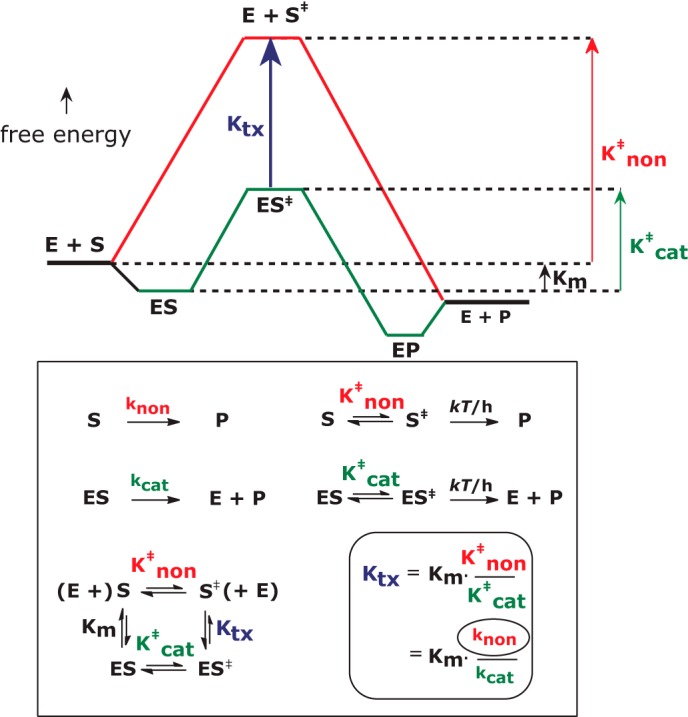
Free energy changes during enzyme catalysis. Estimation of K_tx, the dissociation constant of the enzyme from the altered substrate in the transition state, requires knowledge of k_non, the rate constant of the uncatalyzed reaction in water.

Until fairly recently, the hydrolysis of peptide bonds was the slowest process whose rate had been measured directly in water, with an apparent half-life of 4 years at room temperature (3). That reaction was so slow that its measurement required an extraordinarily sensitive method for detecting extremely early stages in product formation. However, there were reasons to suppose (including, for example, the survival of ancient documents in water) that other biological reactions might be slower still in the absence of a catalyst. An alternative approach to measuring the rates of slow reactions was suggested by a well known rule of thumb, according to which reaction rates tend to double (“Q₁₀ = 2”) when the temperature is raised by 10 °C. In one of the first descriptions of the effect of temperature on the rate of a reaction in water, Harcourt and Esson (4) reported a Q₁₀ of 2 for the well known “iodine clock” reaction, in which an abrupt change from colorless to black makes it possible to perform kinetic measurements with the aid of a simple stopwatch. Compounding that increment, one would expect rates of reaction to increase ∼70-fold when the temperature is raised from 25 °C to the boiling point of water. Even at elevated temperatures, however, the prospects for determining the rates of very slow reactions did not seem bright.

When that approach was first applied to very slow reactions, the results were a surprise. The rule that Q₁₀ = 2 applies to only a few reactions (e.g. the hydration of CO₂) that are rapid and easy to measure at ordinary temperatures. However, slow reactions are vastly more sensitive to temperature. For the decarboxylation of orotidine 5′-phosphate decarboxylase, an intermediate in the biosynthesis of nucleic acids, Q₁₀ is 16. Thus, the rate of this reaction increases not 70-fold as suggested above but 4 million-fold when the temperature is raised from 25° to 100 °C (5). Subsequent experiments have shown that Q₁₀ values are 4 for peptide hydrolysis, 6 for the hydrolysis of simple O-glycosides, 13 for the decarboxylation of orotidine 5′-phosphate decarboxylase, and 16 for the P–O cleavage of phosphate monoester dianions: the reaction catalyzed by fructose-1,6-bisphosphatase and inositol phosphatases. The remarkable sensitivity of slow reactions to temperature, together with the linearity of Arrhenius plots in which the logarithm of the rate constant of a reaction is plotted as a function of the reciprocal of absolute temperature (Kelvin), makes it possible to obtain, by extrapolation, the rates of many reactions that are extremely sluggish at ordinary temperatures (supplemental Fig. S1). Representative half-lives at 25 °C are 7 × 10⁵ years for fumarate hydration, 2.3 × 10⁹ years for uroporphyrinogen decarboxylation, and 1.0 × 10¹² years for the hydrolysis of the dianions of simple phosphate monoesters (6). The value of t_½ for sulfate ester hydrolysis by S–O bond cleavage was recently estimated as 10¹⁸ years (7).

These observations raise two obvious questions. How did such reactions ever get started on the primitive earth? Also, how did enzymes ever evolve to surmount such formidable kinetic obstacles?

Kelvin or Darwin? A Scenario for the Rapid Appearance of Prebiotic Chemistry

In a letter to J. D. Hooker, Darwin imagined how life might have originated, perhaps in a “warm little pond” (8). Shortly after the publication of The Origin of Species, William Thomson (Lord Kelvin) became interested in the age of the earth and set his students to measuring temperatures at various depths in the soil. He used those results to calculate the rate of heat loss from the earth, assuming that the earth began as a molten mass, and estimated the age of the earth as between 20 and 40 million years. In Kelvin's inaugural address as president of the British Association, he stated his conviction that insufficient time had elapsed on Earth for the chemistry of living systems to have attained its present level of complexity without “intelligent and benevolent design” (9).

Had he been aware of the generation of heat by the radioactivity of the earth, a phenomenon that would only be discovered much later, Kelvin would not have underestimated the age of the earth (now known to be ∼4.6 billion years) by a factor of ∼100. It should also be added that he was also unaware that life emerged very early during the life of the planet, probably within the first 0.5–1 billion years. Life began, in the words of Philip Ball, “in a blink, almost the instant the oceans were formed. It is as if it was just waiting to happen — as indeed some have suggested. Although Darwinian evolution needed billions of years to find a route from microbe to man, it seems that going from mineral to microbe took barely a moment” (10). If life began so early, then Kelvin's question regains some of its original force. How could biological chemistry have gotten off to such a quick start?

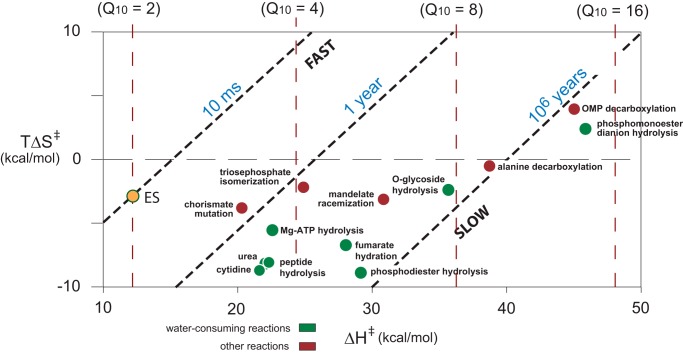
New information emerging from Arrhenius analyses (6) indicates that the more sluggish a reaction is, the more temperature-sensitive it tends to be. The strength of that relationship emerges clearly if one plots the heats of activation (ΔH^‡) of uncatalyzed reactions in water (a measure of the sensitivity to temperature of a reaction) as a function of their free energies of activation (ΔG^‡) at 25 °C (a logarithmic function of the reaction rates) (supplemental Fig. S2).² Alternatively, the entropies of activation (TΔS^‡) of these reactions can be plotted against their enthalpies of activation (Fig. 2). For purposes of orientation, the diagonal broken lines in Fig. 2 show the possible values of ΔH^‡ and TΔS^‡ for reactions that proceed at each of several rates at 25 °C, with t_½ values of 10 ms, 1 year, or 10⁶ years. The vertical “Harcourt line” represents a hypothetical reaction with a Q₁₀ of 2 (see above). The yellow point in this figure represents a typical value observed for enzyme reactions, most of which are very similar as discussed later. A tie-line between that point and any of the other points in Fig. 2 indicates the change in the thermodynamics of activation that the corresponding enzyme must produce. As will be discussed later, enzyme catalysis is usually achieved by making ΔH^‡ more favorable (or less positive), rather than by making TΔS^‡ more favorable (i.e. more positive). Each point in Fig. 2 represents a reaction whose thermodynamics of activation have been reported, and these points are seen to be distributed over a wide range of values of ΔH^‡ (shown horizontally) but over a relatively narrow range of values of TΔS^‡ (shown vertically), i.e. heats of activation play a much more pronounced role in determining the relative rates of these uncatalyzed reactions than do their entropies of activation.

FIGURE 2.

Entropies of activation (TΔS^‡) plotted as a function of enthalpies of activation (ΔH^‡) of some uncatalyzed reactions (11). The yellow point represents an average value for a collection of enzyme reactions (23). OMP, orotidine 5′-phosphate decarboxylase.

Fig. 2 also suggests a likely source of the misleading generalization, the “Q₁₀ = 2.” Rates of reaction are usually convenient to measure if their half-lives fall between 1 min and 1 day at ordinary temperatures, i.e. their ΔG^‡ values fall between 20 and 24 kcal/mol at 25 °C. If TΔS^‡ falls between 0 and −10 kcal/mol, as is the case for most reactions in water (Fig. 2), then the value of ΔH^‡ must fall in the range between 10 and 24 kcal/mol, corresponding to Q₁₀ values between 2 and 4. In view of these constraints of experimental convenience, it is not surprising that these values appear frequently in the earlier literature (11).

It follows that if prebiotic chemistry evolved in an environment that was significantly warmer than it is today, then most chemical processes would have taken place much more rapidly than they do at present. Also, because the rates of the slowest reactions are also the most sensitive to temperature, they tend to converge and become measurable at temperatures not far from the boiling point of water (supplemental Fig. S3).

However, was the earth hot during the early stages of chemical evolution? The early emergence of life on the earth seems consistent with the view that life emerged while the earth was still warm. Even now, numerous organisms thrive at high temperatures in hot springs and undersea thermal vents, and evidence from ribosomal RNA sequences led Woese to his well known proposal (12) that the earliest branches of the tree of life were largely populated by thermophilic organisms. The constitution of the genetic code suggests that the last common ancestor was a thermophile (13), and the illuminating iron-sulfur theory of Wächtershäuser et al. (14) is predicated on the likelihood that life began near thermal vents in the sea. These arguments for a hot origin are necessarily based on retrospective evidence, and it will probably never be possible to repeat the “experiment.” It is, however, possible to test some predictions of this hypothesis. Particularly compelling, in this author's view, are recent experiments showing that when amino acid sequences from modern mesophilic organisms are used to reconstruct the probable amino acid sequences of proteins that served as their common ancestor, the resulting “ancestral” proteins turn out to be similar in activity to modern enzymes but remarkably thermostable, with melting temperatures of 80–90 °C, ∼30° higher than those of their modern counterparts (15, 16).

Taken together, these lines of evidence favor the view that life originated in an environment that we would consider very warm. Those temperatures would have greatly accelerated chemical events on the early earth, collapsing the time required for prebiotic evolution (supplemental Fig. S3) and countering the view that not enough time has elapsed for life to have achieved its present level of complexity.

How Did Enzyme Evolution Get Started? A Hypothesis Based on “Enthalpic” Catalysis

Present day enzymes exhibit rate enhancements as large as 10²¹-fold (see vertical scale, supplemental Fig. S1) (17). Moreover, many enzymes have been found to act on their substrates with second order rate constants that approach the physical limits imposed by enzyme-substrate encounter in solution, with values of k_cat/K_m that approach 10⁹ m⁻¹ s⁻¹(18) and have evolved to “perfection” in that sense. What circumstances would have permitted enzymes to evolve to this present state of near perfection within the limited time available? The magnitude of that problem is evident if one considers the decarboxylation of orotidine 5′-phosphate, an essential step in the biosynthesis of pyrimidine nucleotides, and thus of DNA. This enzyme reaction proceeds with a rate constant of 39 s⁻¹, whereas the half-life is ∼78 million years at 25 °C in neutral solution in the absence of a catalyst (5). If a “primitive” enzyme enhanced the rate of this reaction by a factor of only 10³, 10⁶, or 10⁹, that enzyme would have been unhelpful to a primitive organism in its struggle for existence. How did the earliest enzyme reactions gain a toehold, so that natural selection could begin its work?

Efforts to address that question have been predicated on the conditions of life as we know it, and the barriers to reaction are formidable at ordinary temperatures. However, as in the case of the simple reactions considered above, the picture changes markedly if we consider a much warmer environment in which spontaneous reactions proceed much more rapidly.

Fig. 3 shows the temperature dependence rate of glycoside hydrolysis in the presence and absence of a bacterial α-glycosidase. The enzyme reaction is much more rapid than the uncatalyzed reaction at ordinary temperatures, but it is very much less sensitive to temperature than the spontaneous reaction, so that the rate enhancement (k_cat/k_non) produced by the enzyme (the white area between the lines in Fig. 3) increases with decreasing temperature (19).

FIGURE 3.

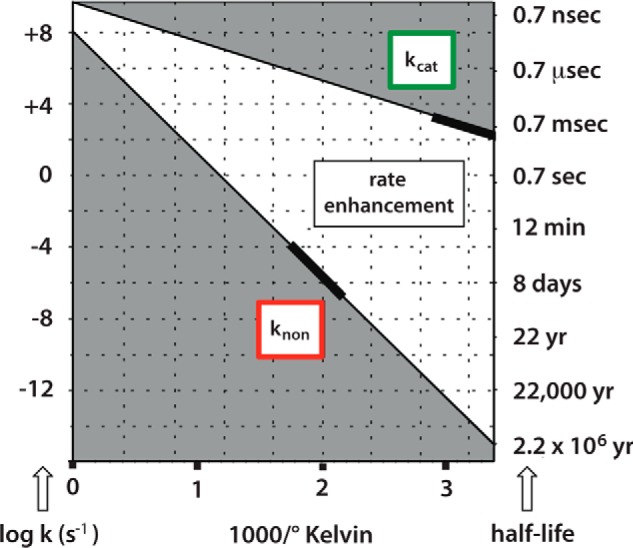
Arrhenius plots for the enzymatic and nonenzymatic α-glucosidase reactions. The bold segments of the line show the temperature range over which rate measurements were conducted (11).

Suppose that a primitive catalyst or proto-enzyme (perhaps a metal ion, or a simple organic acid or base) produced a small enhancement in the rate of a reaction at elevated temperatures. The rate enhancement produced by that catalyst would have increased automatically as the surroundings cooled, quite apart from any improvements that might have resulted from the effects of evolutionary pressure over time.

The plausibility of that scenario depends on whether, and to what extent, a primitive catalyst might have achieved its effect entirely by lowering the enthalpy of activation (supplemental Fig. S4B, blue wedge), as opposed to achieving its effect entirely by enhancing the entropy of activation (supplemental Fig. S4A, orange wedge). Thus, it would be of interest to know whether primitive nonenzymatic catalysts, such as might have been present on the surface of a primitive earth, follow either of those extreme scenarios. Supplemental Fig. S5 compares some nonenzymatic catalysts or nonaqueous environments for which rate enhancements have been reported. These include several proteins (including a catalytic antibody, two designed enzyme mimics, and a designed interface between protein subunits), three metal ions, and nonaqueous environments that include cyclohexane, hexamethylphosphoramide, and the vapor phase. Highlighted in orange are two particularly powerful catalysts acting in water, pyridoxal phosphate (PLP)³ and Ce^IV, which generate rate enhancements that approach those produced by some enzymes (the rate enhancements produced by some enzymes are shown along the right-hand axis of supplemental Fig. S5). PLP is stable at elevated temperatures, serves as a cofactor in a wide variety of biological reactions, and has been shown to catalyze amino acid decarboxylation in the absence of any enzyme (20). The cerium ion Ce^IV, although not known to be involved in any present day biological processes, has been shown to be an extremely effective catalyst of the hydrolysis of phosphoric acid esters (21, 22). When the rate enhancements produced by PLP and Ce^IV were examined as a function of temperature, the effects of these powerful catalysts were found to be based entirely on the reduction of ΔH^‡, whereas their effects on TΔS^‡ were actually somewhat unfavorable (23).

How general is this behavior among nonenzymatic catalysts that act in water? Rate enhancements have been shown to depend primarily on a reduction in ΔH^‡, rather than an increase in TΔS^‡, in general base catalysis by glycolate of the bromination of acetoacetate (24), in general base catalysis of ester aminolysis by amines (25), in Mg^II catalysis of the alcoholysis of ATP (26), in imidazole catalysis of ester hydrolysis (27), and in phase-transfer catalysis of phosphodiester hydrolysis in the presence of cyclohexane (28). Of special interest is the finding that catalytic antibodies for several reactions produce rate enhancements that are entirely enthalpic in origin (29–31). It would be of interest to know whether improvements in the activities of catalytic antibodies or artificial enzymes, which result from the application of selective pressure (or directed evolution) in the laboratory, are accompanied by progressive reductions in the value of ΔH^‡ or by increases in the value of TΔS^‡.

Is this behavior shared by present day enzymes? In fact, it appears that most modern enzymes resemble α-glycosidase (Fig. 3) in that the enthalpy of activation (ΔH^‡) for k_cat is much less positive for the enzyme reaction than for the uncatalyzed reaction. For a randomly chosen set of enzymes catalyzing the cleavage of bonds of seven different types, the value of ΔH^‡ associated with k_cat is reduced by an average value of 16 kcal/mol (23). In contrast, the value of TΔS^‡ increases in some cases and decreases in others. Its average value hardly changes, as can be seen in Fig. 2, where the point marked in yellow represents the average values of ΔH^‡ and TΔS^‡ for a randomly chosen set of enzyme reactions.

It is not enough to consider the effect of temperature on k_cat relative to k_non, because both k_cat and k_cat/K_m are important indices of evolutionary advancement (for example, if the concentration of an enzyme is 10⁻⁸ m, then the value of k_cat/K_m must be at least 10⁸-fold larger than the value of k_non if the enzyme is to produce a simple doubling of the reaction rate). Thus, it is of interest that the effects of changing temperature on enzyme action are even more profound if we consider catalytic proficiency ((k_cat/K_m)/k_non) or transition state affinity (its reciprocal). Supplemental Figs. S6 and S7 show that, for bacterial cytidine deaminase, the values of k_cat and K_m both increase with increasing temperature, and to almost the same extent. Accordingly, k_cat/K_m is almost completely insensitive to temperature, whereas k_non decreases steeply with decreasing temperature. As a result, transition state affinity increases with decreasing temperature to an extent that is even greater than the effect of temperature on the rate enhancement.

A conspicuous exception to this behavior is the peptidyltransferase center of the ribosome, an RNA catalyst that achieves its effect entirely by rendering the entropy of activation more favorable. Interestingly, the ribosome actually renders the enthalpy of activation less favorable. The dominance of entropy in this special case seems understandable in view of the overarching importance of substrate specificity, rather than rate enhancement (the ribosome produces only a modest rate enhancement of 10⁷-fold), in the function of the ribosome. In this interesting case, the enzyme is believed to produce catalysis by “physical” effects, desolvating and juxtaposing the two substrates in a position conducive to reaction, rather than by acting as a covalent or general acid/base catalyst (32, 33).

For the great majority of enzymes, it seems reasonable to suppose that the enthalpic basis of catalysis reflects their origin in more primitive catalysts, for which a reduction of ΔH^‡ (rather than an increase in TΔS^‡) offered a selective advantage in a gradually cooling environment. Although the detailed means by which that was accomplished presumably varied from case to case, its structural basis is explained by the formation of new electrostatic and hydrogen bonds in the transition state, for which much evidence exists in the structures of enzyme complexes with transition state analogue inhibitors (11, 34).

Potential Influences of Temperature on the Incidence of Spontaneous Mutation

Superimposed on these enthalpy-based effects on enzyme activity would have been any improvements in activity that were brought about by mutation and natural selection. High temperatures would be expected to accelerate mutation in at least two ways. First, the familiar melting of DNA and other macromolecules testifies to the thermal instability of the canonical Watson-Crick base pairs. H-bonds are weakened by increasing temperature, as indicated by the adverse effect of increasing temperature on the dimerization of urea (35), and both the stacking and the H-bonding of a terminal AU base pair, in a double-stranded RNA hexamer, have been shown to release heat (36). The resulting increase in the frequency of mispairing would presumably have been greater at high temperatures than it is at present, tending to enhance the frequency of mutation.

Perhaps more importantly, elevated temperatures would be expected to accelerate any irreversible chemical changes that result in spontaneous mutation. Among the more common of those changes are the hydrolytic deamination of cytosine and adenine residues and the hydrolysis of glycosidic bonds that join deoxyribose to the purine nucleobases. Ordinarily, it is not easy to monitor these processes in vivo in the face of sophisticated mechanisms for DNA repair. However, Frederico et al. (37) were able to bypass those difficulties by measuring the rate of reversion to uracil of a specific cytosine residue that had been introduced by mutation of the lacZα gene coding sequence of a bacteriophage. The sensitivity of their assay, based on the recovery of activity of the gene product, was such that reversion could be detected at a frequency of 1 in 10⁵. These investigators showed that in single-stranded DNA, deamination occurs at a rate (and with a heat of activation) similar to the rate of deamination of CMP. They also observed that deamination proceeds 100-fold more slowly in double-stranded than in single-stranded DNA (38). Earlier, several other striking examples of heat-induced mutagenesis in bacteriophage T4 had been described by Drake and his associates (39). Thus, there is synergism between the first and second effects noted above.

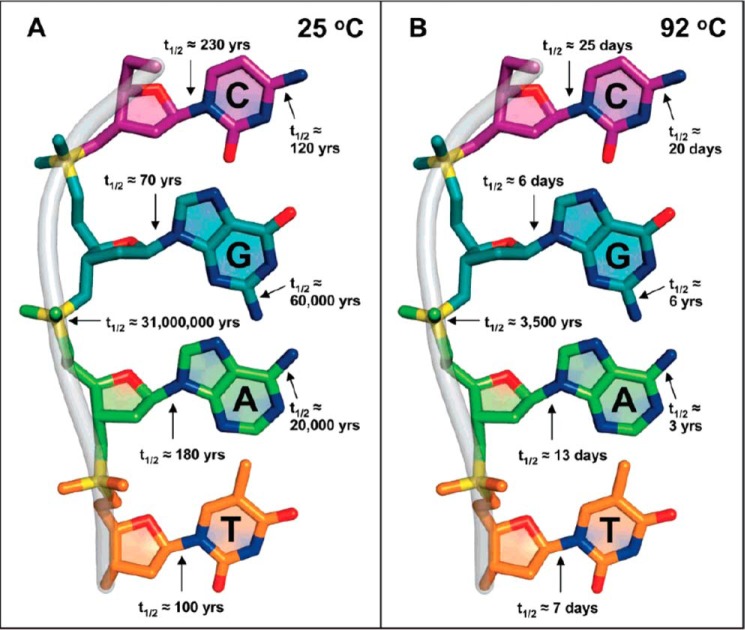
In model studies, the relative sensitivity of mutagenizing events to temperature was examined by Schroeder and Wolfenden (40), with the results shown in Fig. 4. Half-lives for the cleavage of bonds that are present in DNA in neutral solution are shown as room temperature, and also at the elevated temperature at which the hyperthermophilic organism Ignisphaera aggregans grows optimally). Cytosine deamination, for example, proceeds ∼2000-fold more rapidly at 92° than at 25 °C. Notably, the half-lives for the hydrolysis of deoxyribose linkages to purines and pyrimidines, and for the hydrolytic deamination of cytosine derivatives, take place within a few days in neutral solution at elevated temperature. Also, although the phosphodiester linkages of DNA are stable under those conditions, those of RNA decompose at rates that approach the rate of deamination of cytosine derivatives.⁴

FIGURE 4.

Half-lives of bonds in DNA at pH 7, based on work with individual 2′-deoxynucleosides and other model compounds (40).

Conclusion

In summary, it seems probable that in the warm surroundings in which life first appeared, high temperatures would have lowered the kinetic barriers to product formation, and that the activity of weakly active proto-enzymes would have increased automatically as the temperature fell. Elevated temperatures would also be expected to have accelerated the early stages of evolution itself, collapsing the time required for life to attain its present level of complexity.