Evolutionary Aspects of Enzyme Dynamics

Abstract

The role of evolutionary pressure on the chemical step catalyzed by enzymes is somewhat enigmatic, in part because chemistry is not rate-limiting for many optimized systems. Herein, we present studies that examine various aspects of the evolutionary relationship between protein dynamics and the chemical step in two paradigmatic enzyme families, dihydrofolate reductases and alcohol dehydrogenases. Molecular details of both convergent and divergent evolution are beginning to emerge. The findings suggest that protein dynamics across an entire enzyme can play a role in adaptation to differing physiological conditions. The growing tool kit of kinetics, kinetic isotope effects, molecular biology, biophysics, and bioinformatics provides means to link evolutionary changes in structure-dynamics function to the vibrational and conformational states of each protein.

Dihydrofolate Reductase: Coevolving Residues and Their Roles in Catalysis

Genetic analysis of the folA gene, which codes for dihydrofolate reductase (DHFR),⁴ has led to the identification of residues whose evolution was biased (coevolving residues that depend on one another) (1), constituting an evolutionarily coupled network (2). Those residues are not only located in the active site, but span across the protein, and some are far from each other in both sequence and space. The color coding in Fig. 1a represents the level of bias (conserved, strong, or weak coevolution).

FIGURE 1.

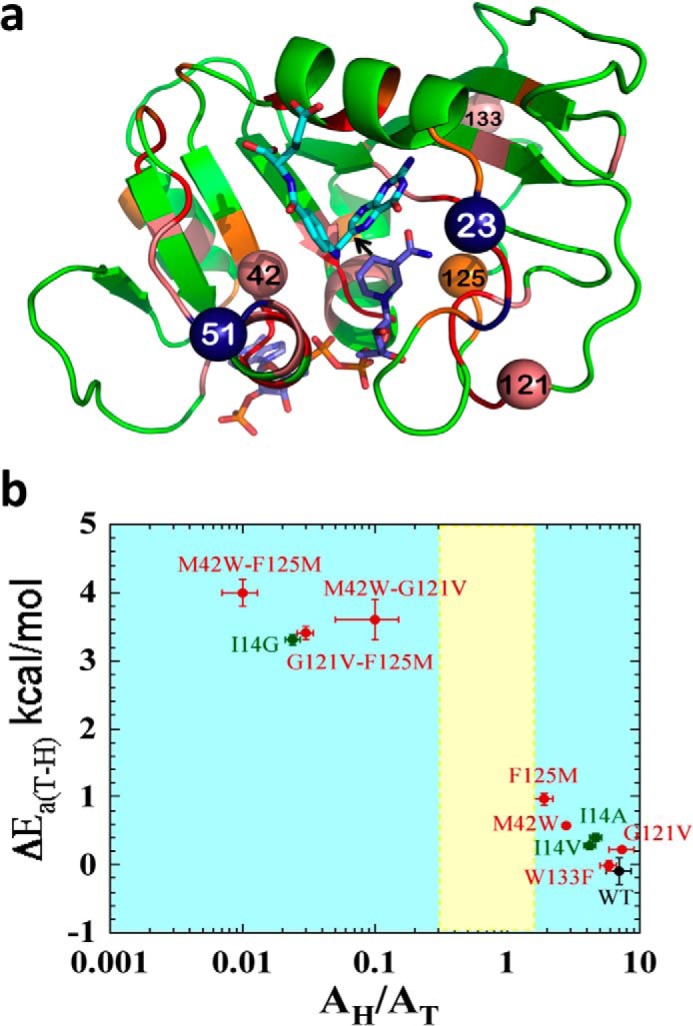
Structural, genetic, and functional features of DHFR. a, DHFR structure (Protein Data Bank (PDB) ID 1rx2) colored based on the genetic coupling analysis as Conserved (red), Strongly Coupled, (pink), and Weakly Coupled, (orange). The nicotinamide cofactor and folate are highlighted as blue and light blue sticks, respectively, and a black arrow is drawn at the location of the C–H→C transfer (between C4 of the nicotinamide to C6 of the pterin). Highlighted as spheres with the same color code are the α-carbons of the four coevolving residues that are discussed in the text above. Highlighted as dark blue spheres are Asn-23 and Gly-51, which are the sites of the evolution-induced insertions discussed below. b, correlation of temperature dependence parameters of T-KIE_int for WT (black), distal (red), and active site Ile-14 (green) mutants of ecDHFR, where error bars represent S.D. The yellow block represents semi-classical range of Arrhenius pre-exponential factor (0.3–1.7) (46). Reproduced from Ref. 12. with permission from the American Chemical Society.

An interesting question is raised by these findings: whether the coevolution of these residues is related to their role in catalyzing the chemical conversion of substrates to products or to other functions of the enzyme (such as binding and release of the reactants, folding, solubility, stability, etc.). Several of the coevolving residues have also been indicated by independent computer simulations to be dynamically coupled to each other and to the reaction coordinate (i.e. the chemical step catalyzed by the enzyme) (3–7). If the networks identified via genetic analysis and the ones identified by calculations are the same, then it would indicate strong evolutionary pressure to preserve the protein dynamics involved in catalyzing the chemical step. Protein dynamics, as presented here, refer to vibrations and conformational fluctuations at timescales ranging from the millisecond turnover of the catalytic cycle (k_cat) to picoseconds or even the femtosecond vibration at the lifetime of the transition state.

To test these hypotheses, the nature of the chemical step for mutants and double mutants was examined for several of the proposed coupled residues (highlighted as spheres in Fig. 1a). Residues Met-42, Gly-121, and Trp-133 are strongly coupled by genetic analysis, whereas Phe-125 is only weakly coupled (using the residue numbers for the DHFR from Escherichia coli, ecDHFR, which was used in all the studies mentioned here). Some of these residues, Met-42, Gly-121, and Phe-125, were independently identified by the calculations to be dynamically coupled to each other and to the reaction coordinate, whereas Trp-133 did not present significant dynamic coupling (3, 4, 6).

A broad range of kinetic methods has been used to test this question. Those methods include measurement of steady state rate constants (i.e. the first order rate constant k_cat and the second order rate constant k_cat/K_m), pre-steady state rate constants from both single turnover and burst experiments, the kinetic isotope effects (KIEs) on these rates (KIE_obs), as well as the intrinsic KIEs (KIE_int) and their temperature dependences. Several different sets of mutants of these residues have been examined, and here we focus on M42W, G121V, F125M, and W133F, and several of their double mutants. The chemistry is only partly rate-limiting for steady state rates of ecDHFR at high pH, and is far from being rate-limiting at pH below 9 (8); thus, these rate constants are not indicative of effects on the chemical step. Pre-steady state rates better reflect the chemical step (i.e. the C–H→C transfer rate) (9). The KIE_obs values and KIE_int values and their temperature dependences for ecDHFR and its mutants have also been reported (10–13).

The outcome of these kinetic experiments indicates strong synergy in the effects of mutants of Met-42, Gly-121, and Phe-125 on the catalyzed chemical conversion (the C–H→C hydride transfer). One indicator for the coupling of these residues to each other and to the chemistry is the comparison of their pre-steady state rates with that of the wild-type (WT) enzyme. If ΔG^‡_i is the free energy difference between the WT and mutant i or j, and ΔΔG^‡_i+j is the free energy difference between the WT and the double mutant i+j, then ΔG^‡_i + ΔG^‡_j < ΔΔG^‡_i+j serves as an indication of synergism between the effect of Met-42, Gly-121, and Phe-125 mutations on the pre-steady state rate (9, 12). W133F, on the other hand, had little effect on the pre-steady state rate, despite a more significant effect on k_cat, indicating that its role lies in product release rather than the chemical step (8).

An even more direct indicator for the effect of these coupled residues on the chemical step is their alteration of the temperature dependence of intrinsic KIE (T-KIE_int) (14, 15). Although the data of the T-KIE_int can be fitted to various theoretical models, there is a broad agreement that for a well defined transition state (TS, or its QM diffused form), the tunneling ready state, TRS (14, 15), leads to temperature-independent KIE_int, as found in most WT enzymes. A temperature-independent KIE_int is associated with a narrow distribution of hydride donor-acceptor distance (DAD) with reduced DAD sampling at the TRS. On the other hand, a very steep T-KIE_int can indicate a broad distribution of DADs typical to poorly defined TRS (16) and increased DAD sampling, as is often observed for mutants or nonphysiological conditions (15). The size of the intrinsic KIE seems to be a sensitive indicator of the average DAD, where a larger KIE results from longer average DADs. In addition to the mutational studies described above, two recent attempts to examine the coupling between the protein dynamics and the DAD distribution compared T-KIE_int between isotopically light versus heavy enzymes (17, 18). The first study found steeper T-KIE_int for the heavier enzymes throughout the temperature range (17), whereas the second found no effect at 20–45 °C temperature range and steeper T-KIE_int at lower temperatures (18). The impact of two different effects of the heavier enzyme on the KIEs makes it difficult to use the findings as clear evidence for protein dynamics directly affecting the DAD; the frequencies of the protein vibrations at the fs-ps timescale (3000–50 cm⁻¹) will be reduced in the heavy enzyme, but the electrostatic modification of the C–H bonds to the more hydrophobic C–D bonds throughout the protein may also lead to different ensembles of protein conformations at the TRS. Both effects could alter the interplay of protein dynamics with the H-transfer coordinate that lead to narrow DAD distribution and small T-KIE_int in the natural enzyme, as well as a steeper T-KIE_int in the heavy enzyme.

Fig. 1b summarizes the results for the T-KIE_int of hydrogen to tritium for the WT and mutants by correlating Arrhenius slopes (ΔE_{a T-H}) and their isotope effects on the Arrhenius pre-exponential factor (A_H/A_T). The data for the WT and W133F reveal a temperature-independent KIE_int of about the same size, and the data for the single mutants indicate a small increase in T-KIE_int values. The three double mutants of M42W, G121V, and W133F, on the other hand, present a very steep T-KIE_int and small A_H/A_T, further revealing the significant impact of those residues on each other and the chemical step. In Fig. 1b, the data are compared with active site mutants of Ile-14 (green), which is located behind the nicotinamide ring (the H-donor) and “pushes” it closer to the folate (the H-acceptor), leading to narrow and short DAD distribution in the WT (16). Fig. 1b reveals that the effect of the single mutants of residues distal from the active site is similar to I14V and I14A, but that the double mutants have as dramatic an effect as I14G, which leads to a very broad and long distribution of DADs at the TRS (16).

It is important to note that experimental testing of all the residues that were predicted by both genetic coupling analysis (1, 2) and high level simulations (3–7) confirmed the functional coupling between them and the catalyzed chemistry. The same analysis for a residue that was only identified by genetic analysis (Trp-133) did not reveal an effect on the chemical step. Although this does not rule out the possibility that this residue is genetically coupled by evolutionary pressure to other residues, it does indicate that its coupled network does not play a role in catalyzing the chemical step (instead perhaps participating in another functional aspect of the protein, such as stability, folding, ligand binding, etc.). The findings bring to mind the possibility that evolutionary pressure can lead to different networks of coevolving residues, but that at least one network can have a role in catalyzing the chemical step.

In conclusion, the examination of evolutionary-dependent (coevolving) residues and a functional network of dynamics coupled to the chemistry catalyzed by the enzyme suggests that coupled residues with a functional role are also coevolving, but not all coevolving residues affect the chemical step. This possibility can be rationalized, as residues may coevolve to maintain other needed properties of the protein, such as folding and solubility.

Dihydrofolate Reductase: Evolution from Bacteria to Human and the Preservation of Functional Dynamics

The evolution of DHFR from bacteria (ecDHFR) to human (hsDHFR) has been examined by phylogenetic analysis of 233 DHFR sequences (19). The values at each divergence node were used to assess the time of divergence for each evolutionary split in units of million years ago. The full set of sequences used is available through the UCSC Genome Browser Wiki Site. That analysis identified several mutations and insertions that were statistically significant along the evolutionary path. Two of the most significant insertions in the hsDHFR were identified as PP at Asn-23 (E. coli numbers) and PEKN at Gly-51 (both highlighted as blue spheres in Fig. 1a). The N23PP mutation altered the enzyme dynamics and was the focus of a heated debate regarding the role of dynamics on different timescales on the chemical step (19–24). The mutant N23PP ecDHFR slowed millisecond motions of the Met-20 loop and slowed the single turnover rates, but did not alter the observed KIEs (KIE_obs) for that rate as reported by Ref. 21, and not even the T-KIE_obs as reported by Ref. 22 (which seem to have contradictory titles, yet consistent findings). More recent studies found that this mutant requires larger motions moving from ground state to transition state (21) and that its T-KIE_int is much steeper than for the WT (23). Together the findings suggest that N23PP ecDHFR has slower motions at the millisecond timescale, but broader distribution of DADs at the TRS and larger motions moving toward its transition state (at the pico- to femtosecond timescale). Interestingly, the N23PP insertion was only introduced in DHFR 325 million years ago (chicken), well after the G51PEKN insertion was introduced 463 million years ago (skate). Similarly, G51PEKX was introduced 797 million years ago (hedgehog), but the first insertion at Asn-23 was only 499 million years ago (hagfish). Mutants of the ecDHFR either with only N23PP or with both N23PP and G51PEKN were examined using different QM/MM calculations (19, 24) and various experimental tools, including steady state and pre-steady state rates, KIE_obs (21, 22), and KIE_int (23), along with the temperature dependences for both KIEs. Both computer simulations suggested that the single mutant N23PP results in an enzyme that does not pre-organize the hydride donor and acceptor very well, and thus many residues across the protein have to be reorganized as the system moves toward its TS (19, 24). Similarly, studies of T-KIE_int revealed that N23PP resulted in an inflated and more temperature-dependent KIE_int, indicating a poorly reorganized reactive complex. However, QM/MM calculations for both the WT ecDHFR and the “humanized” double mutant N23PP/G51PEKN brought the reactants to a state from which minimal reorganization was needed to reach the TS (19), and T-KIE_int measurements with both WT and the double mutant maintained temperature-independent KIE_int (19). Both the calculations of the degree of coupling between residues across the protein (19) and T-KIE_int experiments examine enzyme dynamics at rather small amplitudes and fast frequencies (probably at the picosecond timescale) (10, 14). Given that all of the 233 naturally occurring sequences examined either do not have the N23PP insertion or have both Asn-23 and Gly-51 insertions, it is likely that evolutionary pressure maintains the protein vibrational/conformational landscape that brings the H-donor and acceptor to an ideal orientation.

The effects of these single and double insertions on steady state rates also fit the same pattern, as do the pre-steady state pH-independent rates (i.e. the single mutant was slower and the WT and double mutant have similar kinetic parameters) (23). As those kinetic parameters reflect motions at the millisecond timescale (including the rate-limiting step for the overall catalytic cycle (8), it is likely that evolutionary pressure applies across a hierarchy of timescales. The only reported parameter that was not affected by the single mutation was the KIE_obs on the pre-steady state rate (21) and temperature dependence of that KIE_obs (23). Kinetic analysis of that parameter revealed that temperature-dependent kinetic complexity deflated KIE_obs for both WT and the single mutant but with different values and different temperature dependences. This kinetic complexity reflects the ratio between the isotopically sensitive step forward and microscopic rate constants along the backward decomposition of the reactive complex. The different kinetic complexities of the WT and N23PP may very well represent motions at the millisecond timescale that are altered by the mutation, as has also been indicated by NMR experiments (21). Unfortunately, such data are not yet available for the double mutants, so our knowledge regarding the effect of the double mutant on the millisecond timescale is limited to the fact that its pH-independent pre-steady state rate is as fast as the WT (∼1000 s⁻¹), whereas the N23PP single mutant is slower (∼35 s⁻¹), as are its millisecond vibrations (21).

In conclusion, the studies of the WT and humanized ecDHFRs, together with the results of phylogenetic analysis, suggest that the enzyme dynamics evolved to optimize the catalyzed reaction. These studies reveal a possible evolutionary conservation of functional dynamics at different timescales and their role in the enzyme-catalyzed reaction.

Prokaryotic Alcohol Dehydrogenases as a Model for Protein Adaptation

The prokaryotic alcohol dehydrogenases constitute a family of highly homologous enzymes that function within different temperature niches. This family includes enzymes from psychrophilic (ps-ADH), mesophilic (ec-ADH), and thermophilic sources (ht-ADH) (25–28). Although it has been speculated that thermophilic prokaryotes may be among the earliest life forms (29), studying the behavior of this family of dehydrogenases is not predicated on a timeline for temperature adaptation. Rather the focus is toward understanding how the introduction of a new exigency (such as a change in ambient temperature) can produce evolutionary change at the level of protein function. The sequence identity between the orthologs that function at extreme temperature (ps-ADH from the Antarctic Moraxella sp. TAE123 and ht-ADH from Bacillus stearothermophilus) is 61% (76% similar), and the three-dimensional backbone structures for these two enzymes are effectively superimposable (26–28). Observed changes in functional properties at the temperature extremes of ht-ADH and between ht- and ps-ADH are likely, thus, to arise from subtle changes in protein flexibility/motions.

Tools developed initially for kinetic studies of eukaryotic ADHs included characterizing alcohol substrates for which the hydride transfer was fully rate-determining (30, 31). Using this approach with ht-ADH, a temperature-dependent break in the steady state kinetics that extended to the magnitude of primary and secondary deuterium KIEs was observed (32). Of particular note is the presence of a temperature independence for the primary KIEs above 30 °C that segues to temperature-dependent KIEs below 30 °C. These early studies were initially interpreted as a change in the contribution of hydrogen tunneling to the reaction coordinate under physiological (>30 °C) versus nonphysiological (<30 °C) conditions. Retrospectively, and with the benefit of a much larger body of experimental data (e.g. Refs. 33 and 34), the KIE behavior of ht-ADH is now concluded to reflect a role for protein motions in the H-transfer step. Above 30 °C, where the protein is optimally flexible, protein sampling of the conformational landscape produces pre-organized states that transiently generate a highly structured and tunneling-ready hydrogen DAD. Below 30 °C, a rigidification of protein prevents optimal alignment of the H-donor and acceptor, with catalytic recovery requiring a distance sampling mode that has a higher activation energy for deuterium than protium transfer (35, 36).

Subsequent time- and temperature-dependent analyses of hydrogen/deuterium (H/D) exchange from solvent D₂O into the peptide backbone of protein (via mass spectrometric analysis of peptides representing >95% of the ht-ADH sequence) revealed a temperature-dependent break in the protein dynamic behavior as well (37). In particular, five peptides that form an extended β sheet from one of the dimer interfaces of the tetrameric ht-ADH to the substrate-binding site undergo a transition in behavior that correlates with catalysis. The fact that a similar temperature-dependent change (at 30 °C) can be observed by H/D exchange with apo-enzyme and on k_cat (condition of saturating cofactor and substrate) supports the view of overlapping conformational landscapes for free versus substrate-bound proteins (38, 39). The mapping of the H/D exchange behavior onto the three-dimensional structure of ht-ADH (Fig. 2a), indicates the highly anisotropic nature of temperature-dependent changes in protein flexibility that correlate with catalysis (37).

FIGURE 2.

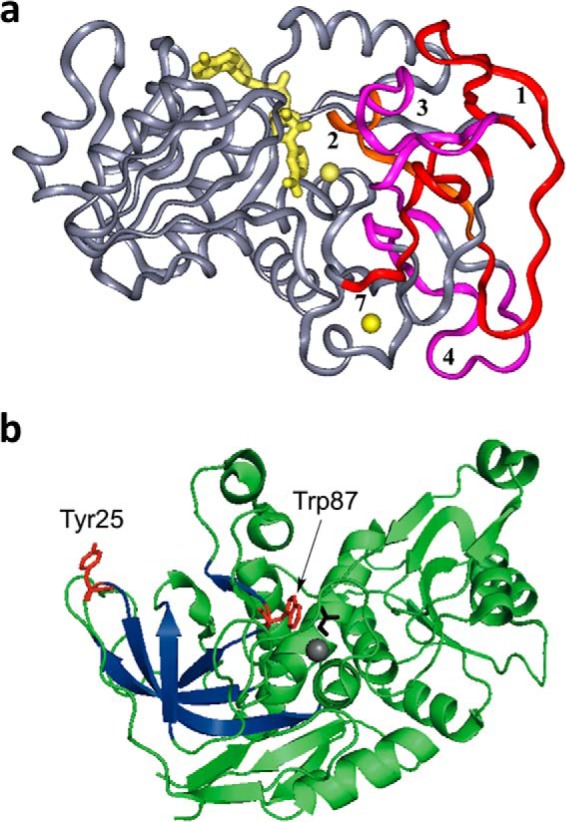
Structural features of ht-ADH. a, the five peptides (1–4 and 7) that increase their flexibility above 30 °C in ht-ADH reside within the substrate-binding site and are colored orange and fuchsia. The cofactor NAD⁺ has been modeled into the active site and is colored yellow, as are the catalytic zinc ion (near the nicotinamide ring of cofactor) and the structural zinc ion. Reproduced with permission from (37), copyright (2004) National Academy of Sciences, U.S.A. b, the relationship of the surface Tyr-25 (red) to the active site Trp-87 (red). Bound substrate, adjacent to Trp-87, is black. The series of β-sheets that increase their flexibility above 30 °C (see a above) are colored dark blue.

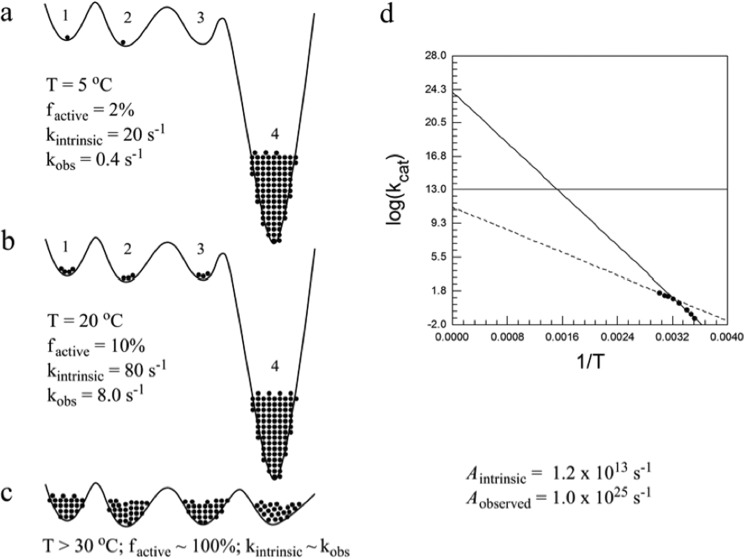
One property of the low temperature kinetic behavior of hydride transfer in ht-ADH is an elevated Arrhenius pre-factor, in excess of the semi-classical limit of ∼10¹³ s⁻¹, that accompanies an ∼7 kcal/mol increase in the enthalpy of activation. Insight into the physical origins of this phenomenon has emerged from studies in which two hydrophobic side chains that reside behind the cofactor nicotinamide ring of cofactor (Leu-176 and Val-260) are reduced in size via site-specific mutagenesis (40, 41). These alterations have relatively little impact on catalytic behavior above 30 °C, but below 30 °C result in enormous elevations in the experimental energies of activation and the Arrhenius pre-factors, with the latter achieving values as high as 10²⁵ s⁻¹ (40). A physical model has been advanced in which the combination of low temperature- and site-specific mutagenesis leads to a greatly impaired conformational landscape (Fig. 3). Accordingly, the protein is postulated to become trapped within low enthalpy states from which it must emerge to achieve effective H-transfer. Because escape from enthalpic traps also leads to an increase in the number of available protein conformational sub-states, the magnitudes of E_a and A_obs increase in a concerted manner. This new type of behavior (Table 1) and the accompanying mathematical model (40) offer a tool for assessment of changes in global protein mobility as it affects catalysis. Specifically, changes in conformational landscapes are proposed to reveal themselves as correlated increases/decreases in the activation parameters E_a and A_obs. A similar pattern has recently been seen when contrasting a smaller, less active prokaryotic lipoxygenase (42) with a eukaryotic ortholog (33). The major structural difference between the prokaryotic and eukaryotic enzymes appears to reside with the size of surface loops rather than with conserved residues in the active site.

FIGURE 3.

A diagram illustrating the distribution of conformational sub-states as a function of temperature in ht-ADH. Reproduced with permission from Ref. 40, copyright (2011) National Academy of Sciences, U.S.A. a–c indicate the redistribution of enzyme from an inactive region of the conformational landscape (state 4) into the regions that can support hydride transfer (states 1-3) as the temperature is raised above 30 °C. The mathematical model treats the rate as a function of a temperature-dependent equilibration, K_eq, and the rate constant, k_intrinsic. d shows the ability to achieve A_observed = 10²⁵ s⁻¹ via a compensatory increase in ΔH^‡ and TΔS^‡. The extrapolation to A_intrinsic is shown by the dashed line, and the extrapolation to A_observed is shown by the solid line.

TABLE 1.

Illustrative patterns in the Arrhenius activation parameters for ht-ADH and ps-ADH below 30 °C

From Refs. 40, 47, and 50.

ADH ortholog	ΔH‡	log(Aobs)	TΔS‡, 30 °C	KIE, 30 °C
	kcal/mol		kcal/mol
ht-ADH
WT	21.4	17	5.6	3.2
L176A	25.8	19	8.8	4.1
L176del	34.8	25	16.5	4.3
V260A	32.3	24	15.4	4.1
ps-ADH	9.2	8	−7.5	4.0a

^a At 20 °C; the comparable KIE for ht-ADH at this temperature is 5.0.

The behavior of ht-ADH as a function of temperature- and site-specific mutagenesis highlights two distinct classes of protein motions that are expected to contribute to catalytic fitness. One is a global sampling of the conformational landscape (reflected in the noncanonical activation parameters at low temperature), whereas the other is optimization of the DAD of the reactants (reflected in the degree to which KIEs become temperature-dependent when enzymes are perturbed away from optimal conditions for function). From fitting of enzymatic H-tunneling parameters, the latter is shown to be dominated by fairly fast (nanoseconds to picoseconds) timescales (33), whereas the conformational search for catalytically optimal configurations is expected to span a broad hierarchy of timescales (43).

The successful achievement of temporal, as well as spatial, resolution that links protein motions to catalysis is the “gold ring” in our ability to predict and understand the dynamical bases for functional evolution in proteins. The interrogation of H/D exchange in ht-ADH, although introducing spatial resolution for the contribution of protein flexibility to hydride transfer, does not provide a direct measure of a kinetic process for protein motions. This is because the measurements were collected under EX2 conditions, thereby reflecting an equilibrium distribution of partially unfolded protein that permits deuterium exchange into the peptide backbone (44). Time-resolved fluorescence methods offer a means to interrogate more rapid protein motions using either intrinsic or extrinsic fluorescence probes. In the case of ht-ADH, protein variants have recently been generated that contain a single tryptophan either at in the substrate-binding domain (Trp-87) (Fig. 2b) or in a remote position at the protein surface (Trp-167); both single Trp variants retain the catalytic break near 30 °C of the WT enzyme (45). Exploration of fluorescence lifetimes and time-dependent Stokes shifts with these constructs has uncovered a distributed network of protein side chains, extending across >30 Å,⁵ that undergoes changes in fast, local motions (nanoseconds to picoseconds) in response to a reduction in temperature that is coupled to the introduction of catalysis-affecting mutations.⁵ These fluorescent measurements, on a timescale 10⁶-fold faster than catalysis and more than 10⁹-fold faster than H/D exchange experiments, provide an elegant means of detecting subtle changes in local protein dynamics that arise from a redistribution of the protein micro-states contributing to the global protein conformation landscape.

In conclusion, the rigidification of a thermophilic alcohol dehydrogenase that takes place at reduced temperatures has afforded unique insight into the importance of the protein conformational landscape in optimizing hydride transfer catalysis. This example of enzyme adaptation to an environmental contingency may provide clues regarding possible physical pathways that enable highly evolved catalysts to emerge from more primitive precursors.

Interconverting Thermophilic and Psychrophilic Alcohol Dehydrogenases Uncovers a Link between a Protein Dimer Interface and Active Site Dynamics

Kinetic comparison of the ps-ADH to ht-ADH in the low temperature regime indicates that hydride transfer is equally rate-determining for both enzymes (KIEs of 4–5 at 20 °C), although with different activation parameters (47) (Table 1). The finding that the net ΔG^‡ is identical for the two protein variants is yet another example of the frequently documented pattern of enthalpy/entropy compensation in proteins (48, 49). The property of increased values for E_a and A_obs for ht-ADH relative to ps-ADH in the low temperature regime is analogous to the trends seen for ht-ADH following the introduction of single site mutants, implicating increased rigidity and impaired conformational sampling in ht-ADH relative to ps-ADH. Comparative analysis of H/D exchange into peptides derived from ps-ADH to ht-ADH at 10 °C has further shown an enhanced flexibility in the region surrounding the active site of ps-ADH that is accompanied by a more rigid protein periphery (27).

Insight into the structural bases for the changes in kinetic and H/D exchange properties in ps-ADH comes from inspection of the available x-ray structures for the two extremophilic ADHs (26–28). One notable feature is the replacement of a π-stacked tyrosine (Tyr-25) at a dimer interface in ht-ADH by alanine (Ala-25) in ps-ADH. In ht-ADH, Tyr-25 resides at the end of the extended β sheet that was previously shown to undergo a selective increase in flexibility above 30 °C (Fig. 2); this residue connects the protein dimer interface to the substrate-binding pocket that is proximal to Trp-87. Targeting position 25 experimentally, the thermophilic and psychrophilic forms of ADH were interconverted, via the replacement of Tyr-25 by Ala in ht-ADH and Ala-25 by Tyr in ps-ADH (50). The impact of these interconversions is dramatic, with Y25A ht-ADH losing the characteristic break in kinetic behavior for WT ht-ADH below 30 °C, whereas the A25Y variant of ps-ADH experiences a break at ∼20 °C that is accompanied by a change in rate-determining step (with hydride transfer becoming increasingly less rate-determining as the temperature is reduced). One feature accompanying the kinetic changes seen for A25Y ps-ADH is a dramatic increase in its thermostability, up to 50 °C (50).

From a structural perspective, the four Tyr-25 residues, one from each monomer, generate a “capstone,” ∼25 Å away from the active site zinc ion at the intersection of the substrate and cofactor-binding sites. The presence of this Tyr-based capstone both increases ps-ADH stability at elevated temperatures and leads to a loss of conformational flexibility in ht-ADH at low temperatures. Although increased thermal stability can be rationalized, at least in part, from the π-stacking interaction between each pair of tyrosines at the protein apex, the origin of the impact of position 25 on active site flexibility is more difficult to discern. Insight into the physical origins of the latter comes from an analysis of a variant of ht-ADH in which Trp-87 within the substrate-binding site is converted to Ala (50). Analogous to Y25A, the replacement of Trp-87 by a smaller side chain in ht-ADH completely eliminates the kinetic break below 30 °C characteristic of WT enzyme. This result shows that altering an amino acid side chain at either end of the extended β raft that connects the dimer interface to the substrate-binding site produces the same kinetic end point. Furthermore, the W87A variant has become thermally unstable, with an increased probability of dissociating into inactive subunits.

Early efforts to understand thermal adaptation in proteins were focused on changes in static, structural elements (51, 52). By contrast, the described studies of ps- and ht-ADH implicate a long range network between Tyr-25 and Trp-87 that directly links protein stability to active site flexibility and catalytic efficiency. At this juncture we do not yet understand the detailed physical origin of the cooperative change in properties in ht-ADH at 30 °C. One possible explanation is a type of cold denaturation (53, 54) that disrupts the arrangement of the π-stacked tyrosine dimers within the capstone. In this context, the x-ray structural data for ht-ADH collected at cryogenic temperatures may be expected to represent enzyme in its catalytically impaired configuration. Future x-ray studies of the tetrameric ADHs at or above 30 °C may prove quite informative regarding subtle structural rearrangements that control the communication of protein dynamics to the enzyme active site (55).

In conclusion, the adaptation that leads to the interconversion of thermophilic and psychrophilic alcohol dehydrogenases is shown to reside within a dynamical network that involves a discrete region of protein extending from a subunit interface to the active site.

Concluding Remarks

The two examples of hydride transfer presented herein have permitted a direct analysis of the role of protein structure and dynamics on the catalyzed chemical step. Mature enzymes appear to evolve their dynamical motions to generate active site configurations that are highly constrained to the internuclear distance and charge requirements optimal to the bond cleavage reaction coordinate. These functional dynamics can span across the protein, undergoing either conservation or coevolution within families of proteins. With the fast increasing volume of genomic and proteomic data, it will be fascinating to examine further the molecular, mechanistic, and biophysical aspects of such evolutionary effects. Future functional applications may include understanding/overcoming the development of drug resistance in pathogens and cancers, the accelerated in vitro evolution of enzymes, and the ab initio design of enzymes with high activity.

For many highly evolved enzymes, the chemical step is not rate-limiting for either catalytic turnover (k_cat) or the second order reaction of enzyme with substrate (k_cat/K_m); in some cases, this is also true during single turnover conditions. It is frequently asked why there would be an evolutionary pressure on steps in enzyme reactions that are no longer rate-limiting. A reasonable view is that chemistry would have been rate-limiting initially in solution and, presumably, also in primitive enzymes. Such primitive enzymes would have needed to evolve the catalysis of chemical step(s) by carefully tuning the dynamics of each system to bring the reactants into ideal orientations and within short DADs. As the chemical step(s) became faster, and other kinetic events began to be more rate-limiting (e.g. reactant binding, product release, protonation/deprotonation, protein pre-arrangement, etc.), pressure to preserve optimal catalysis of the chemical steps would have remained. In the absence of such evolutionary pressure, random mutations that disrupted a high level of fine-tuning of chemical catalysis would have interfered with the earlier rate accelerations achieved by alterations in the structure and dynamics of a protein.